Содержание:
- § 1 Виды треугольников
- § 2 Прямоугольный треугольник
- § 3 Стороны прямоугольного треугольника
- § 4 Площадь прямоугольного треугольника
- § 5 Краткие итоги урока
§ 1 Виды треугольников
В этом уроке научимся находить площадь прямоугольного треугольника.
Давайте отправимся в страну «Геометрия» в город треугольников. Здесь всё треугольное: и дома, и деревья, и даже жители. На первый взгляд, эти жители все очень похожи: у них по три угла, три стороны и три вершины. Но при этом все они отличаются друг от друга. Давайте рассмотрим некоторые из них:
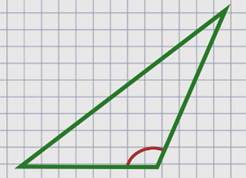
Этот треугольник тупоугольный,
в нем содержится тупой угол.
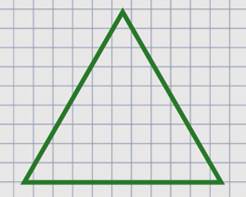
Это равносторонний треугольник –
у него все стороны равны.
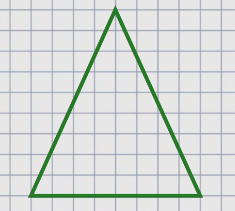
А вот треугольник, у которого равны две стороны.
Его называют равнобедренным.
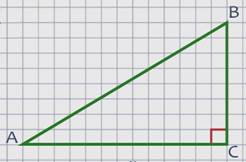
А это треугольник,
в котором угол С – прямой.
Такой треугольник называют прямоугольным.
§ 2 Прямоугольный треугольник
С прямоугольным треугольником мы познакомимся поближе.
Но сначала давайте решим задачу.
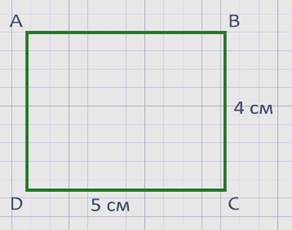
Дан прямоугольник АВСD со сторонами 5 см и
4 см. Нужно найти площадь этого прямоугольника.
Вспомним формулу нахождения площади прямоугольника.
Формула – это верное равенство, устанавливающее взаимосвязь между величинами.
Чтобы найти площадь прямоугольника, нужно длину умножить на ширину (S = a× b). Значит, S = 5 × 4 =20см2.
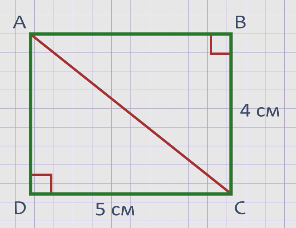
Теперь возьмём наш прямоугольник и проведём в нём диагональ АС.
Диагональю прямоугольника называется любой отрезок, соединяющий две вершины противоположных углов прямоугольника.
Мы видим, что диагональ разделила наш прямоугольник на два одинаковых треугольника. Оба эти треугольника прямоугольные, так как каждый из них содержит прямой угол.
Теперь можно легко найти площадь каждого из этих треугольников. Нужно просто площадь прямоугольника разделить пополам. Значит, площадь каждого из этих треугольников будет равна
S∆ = 20 : 2 = 10 см2.
У нас получилось, что площадь прямоугольного треугольника равна половине площади прямоугольника.
S∆ = (a × b) : 2
§ 3 Стороны прямоугольного треугольника
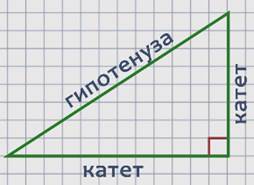
Стороны прямоугольного треугольника имеют свои названия, давайте с ними познакомимся.
Стороны прямоугольного треугольника, образующие прямой угол, называются катетами, а сторона, которая лежит напротив прямого угла, называется гипотенузой.
Чтобы легче было запомнить, можно выучить небольшие стихи о катетах и гипотенузе.
Мы два брата-стороны, катетами названы.
Болтаем мы о том, о сём, сходясь в вершине в углу прямом.
Гипотенуза – я, особый элемент, длинней меня сторон здесь просто нет.
Меня найти нетрудно, право слово,
Лежу напротив я угла прямого.
§ 4 Площадь прямоугольного треугольника
Теперь выведем правило нахождения площади прямоугольного треугольника, зная, как называются его стороны.
Площадь прямоугольного треугольника равна половине произведения его катетов.
S∆ = (a × b) : 2
где a и b – катеты прямоугольного треугольника.
Рассмотрим нахождение площади прямоугольного треугольника на примере.
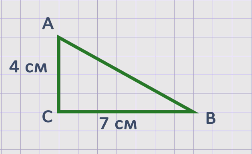
Нам дан треугольник АВС.
Сначала измерим его катеты.
Катет АС = 4 см, катет СВ = 7 см.
Вспомним правило нахождения площади прямоугольного треугольника.
Площадь прямоугольного треугольника равна половине произведения его катетов.
S∆ = (a × b) : 2
Эту формулу необходимо запомнить.
Подставим в неё вместо букв значения.
Получим:
S∆ = (4 × 7) : 2 = 28 : 2 = 14 см2.
Используя данные знания, Вы сможете вычислять площадь и других фигур, разделив их на знакомые фигуры, площадь которых Вы уже умеете вычислять.
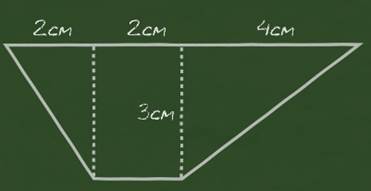
Давайте найдём площадь трапеции.
Для этого мы разделим её вертикальными линиями на прямоугольник и два прямоугольных треугольника, как показано на рисунке.
Найдём сначала площадь прямоугольника. Его длина – 3 см, ширина – 2 см.
Вспомним формулу нахождения площади прямоугольника.
Чтобы найти площадь прямоугольника, надо длину умножить на ширину S = a× b .
Выполняем первое действие:
1) 3 × 2 = 6 см2 – S прямоугольника.
Теперь находим площади треугольников. Вспомним формулу нахождения площади прямоугольного треугольника.
Площадь прямоугольного треугольника равна половине произведения его катетов.
S∆ = (a × b) : 2
где a и b – катеты прямоугольного треугольника
Найдём площадь левого треугольника, его катеты 2 см и 3 см.
2) (2 × 3) : 2 = 3 см2 – площадь левого треугольника.
Найдём площадь правого треугольника. Его катеты 3 см и 4 см.
3) (3 × 4) : 2 = 6 см2 – площадь правого треугольника.
Чтобы узнать площадь всей фигуры, надо сложить площади этих трёх фигур.
4) 6 + 3 + 6 = 15 см2 – площадь трапеции.
Ответ: площадь трапеции равна 15 см2.
§ 5 Краткие итоги урока
Подведем итоги нашего урока:
Чтобы вычислить площадь прямоугольного треугольника, необходимо:
1.Найти у треугольника катеты (это стороны, образующие прямой угол).
2.Определить их длину.
3.Вспомнить формулу нахождения площади прямоугольного треугольника. Площадь прямоугольного треугольника равна половине произведения его катетов.
S∆ = (a × b) : 2
4.Подставить в формулу вместо букв их значения.
5.Вычислить значение получившегося выражения, т.е. площади.
Список использованной литературы:
- Автор конспекта: Курманаева Светлана Валентиновна
- Петерсон Л.Г. Математика. 4 класс. Часть 1./Л.Г. Петерсон. – М.: Ювента, 2014.
- Математика. 4 класс. Методические рекомендации к учебнику математики «Учусь учиться» для 4 класса. / Л.Г. Петерсон. – М.: Ювента, 2014. – 280 с.: ил.
- Зак С.М. Все задания к учебнику математики для 4 класса Л.Г. Петерсон и комплекту самостоятельных и контрольных работ. ФГОС. – М.: ЮНВЕС, 2014.
В этом онлайн уроке рассказывается о том, как найти площадь треугольника ABC (прямоугольного, с тупым углом, остроугольного), формула. Начинается обучение с нахождения площади прямоугольного треугольника, т.е. треугольника, в котором один угол равен 90 градусов. Площадь в этом случае вычисляется по очень простой формуле. Она равна половина произведения длин катетов, т.е. двух сторон прилегающих к прямому углу. Справедливость данной формулы объясняется тем, что любой прямоугольный треугольник можно достроить до прямоугольника, добавив точно такой же треугольник. А площадь прямоугольника вычисляется как произведение его длины на ширину, которые являются катетами составляющих его прямоугольных треугольников. Затем в видео уроке объясняется то, как найти площадь треугольника ABC с тупым и с острым углом. Площадь любого треугольника равна половине его основания умноженное на высоту. Эта формула легко доказывается, основываясь на формулу нахождения площади прямоугольного треугольника Видео урок «Как найти площадь треугольника ABC (прямоугольного, с тупым углом, остроугольного), формула» вы можете смотреть онлайн в любое удобное время совершенно бесплатно. Успехов!
- Длительность: 11:02
- Рейтинг: 3.9/21
- 1
- 2
- 3
- 4
- 5
Если у Вас есть качественные видео уроки, которых нет на нашем сайте, то Вы можете добавить их в нашу коллекцию. Для этого Вам необходимо загрузить их на видеохостинг (например, YouTube) и добавить код видео в форму добавления уроков. Возможность добавлять свои материалы доступна только для зарегистрированных пользователей.
Как найти площадь треугольника – все способы от самых простых до самых сложных
Зависит от того, какой треугольник.
Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.
Если треугольник прямоугольный
То есть один из его углов равен 90 градусам.
Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.
Если он равнобедренный
То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.
Если он равносторонний
То есть все три стороны равны. Ваши действия такие:
- Найдите квадрат стороны – умножьте эту сторону на нее же. Если у вас сторона равна 4, умножьте 4 на 4, будет 16.
- Умножьте полученное значение на корень из 3. Это примерно 1,732050807568877293527.
- Поделите все на 4.
Если известна сторона и высота
Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.
Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.
Если известны две стороны и градус угла между ними
Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:
Если известны длины трех сторон
- Найдите периметр. Для этого сложите все три стороны.
- Найдите полупериметр – разделите периметр на два. Запомните значение.
- Отнимите от полупериметра длину первой стороны. Запомните.
- Отнимите от полупериметра длину второй стороны. Тоже запомните.
- Отнимите от полупериметра длину третьей стороны. И ее запомните.
- Умножьте полупериметр на каждое из этих чисел (разницу с первой, второй и третьей стороной).
- Найдите квадратный корень.
Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.
Если известны три стороны и радиус описанной окружности
Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.
Если известны три стороны и радиус вписанной окружности
Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.
Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.
Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.
Нахождение площади треугольника
Условие задачи для наглядности изображается схематически. Площадь треугольника определяется как половина произведения его основания на высоту. Так как высота задана по условию, то необходимо определить величину основания. В ходе решение используется следующее правило: средняя линия треугольника, соединяющая середины двух сторон, параллельна третьей стороне и равна ее половине. Тогда, зная значение средней линии по условию задачи, определяется величина основания треугольника. Таким образом, все необходимые данные для определения площади треугольника известны. Подставив их в формулу, определяется искомая величина площади.
Как найти площадь треугольника
О чем эта статья:
8 класс, 9 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
Площадь — это численная характеристика, которая дает нам информацию о размере части плоскости, ограниченной замкнутой геометрической фигурой.
Если значения заданы в разных единицах измерения длины, мы не сможем узнать, какая площадь треугольника получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
Популярные единицы измерения площади:
- квадратный миллиметр (мм 2 );
- квадратный сантиметр (см 2 );
- квадратный дециметр (дм 2 );
- квадратный метр (м 2 );
- квадратный километр (км 2 );
- гектар (га).
Формула площади треугольника
Для решения задач применяются различные формулы, в зависимости от известных исходных данных. Далее мы рассмотрим способы решения для всех типов треугольников, в том числе частные случаи для равносторонних, равнобедренных и прямоугольных фигур.
Быстро вычислить площадь треугольника поможет наш онлайн-калькулятор. Просто введите известные вам значения и получите ответ в метрах, сантиметрах или миллиметрах.
Научиться быстро щелкать задачки на нахождение площади треугольника помогут курсы по математике от Skysmart!
Общая формула
1. Площадь треугольника через основание и высоту
, где — основание, — высота.
2. Площадь треугольника через две стороны и угол между ними
, где , — стороны, — угол между ними.
3. Площадь треугольника через описанную окружность и стороны
, где , , — стороны, — радиус описанной окружности.
4. Площадь треугольника через вписанную окружность и стороны
, где , , — стороны, — радиус вписанной окружности.
Если учитывать, что — это способ поиска полупериметра, то формулу можно записать следующим образом:
5. Площадь треугольника по стороне и двум прилежащим углам
, где — сторона, и — прилежащие углы.
6. Формула Герона для вычисления площади треугольника
Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.
, где , , — стороны, — полупериметр, который можно найти по формуле:
Для прямоугольного треугольника
Площадь треугольника с углом 90° по двум сторонам
Площадь треугольника по гипотенузе и острому углу
, где — гипотенуза, — любой из прилегающих острых углов.
Гипотенузой принято называть сторону, которая лежит напротив прямого угла.
Площадь прямоугольного треугольника по катету и прилежащему углу
, где — катет, — прилежащий угол.
Катетом принято называть одну из двух сторон, образующих прямой угол.
Площадь треугольника через гипотенузу и радиус вписанной окружности
, где — гипотенуза, — радиус вписанной окружности.
Площадь треугольника по отрезкам, на которые делит вписанная окружность его гипотенузу
, где , — части гипотенузы.
Площадь прямоугольного треугольника по формуле Герона
, где , — катеты, — полупериметр, который можно найти по формуле:
Для равнобедренного треугольника
Вычисление площади через основание и высоту
, где — основание, — высота, проведенная к основанию.
Поиск площади через боковые стороны и угол между ними
, где — боковая сторона, — угол между боковыми сторонами.
Площадь равностороннего треугольника через радиус описанной окружности
, где — радиус описанной окружности.
Площадь равностороннего треугольника через радиус вписанной окружности
, где — радиус вписанной окружности.
Площадь равностороннего треугольника через сторону
Площадь равностороннего треугольника через высоту
Таблица формул нахождения площади треугольника
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу, использовать как закладку в тетрадке или учебнике и обращаться к ней по необходимости.
[spoiler title=”источники:”]
http://www.virtualacademy.ru/lesson/847/
http://skysmart.ru/articles/mathematic/ploshad-treugolnika
[/spoiler]
Математика 4 Площадь прямоугольного треугольника
4 класс, 25 урок, Площадь прямоугольного треугольника
Площадь треугольника.
Добавить комментарий
Новые уроки
- Видеоурок красивое соло на гитаре
- Упражнения для упругих ягодиц в домашних условиях для девушек видео уроки
- Лунный маникюр шеллаком видео уроки для начинающих
- Видеоурок зарапин
- Укладка плитки видеоурок
Архивы
- Декабрь 2018
- Ноябрь 2018
- Октябрь 2018
- Сентябрь 2018
- Август 2018
- Июль 2018
- Июнь 2018
- Май 2018
- Апрель 2018
- Март 2018
- Февраль 2018
- Январь 2018
Copyright © 2023 Бесплатные видео уроки онлайн