Содержание:
- § 1 Теорема о площади треугольника
- § 2 Следствия теоремы о площади треугольника
§ 1 Теорема о площади треугольника
В этом уроке познакомимся с теоремой о площади треугольника, запишем формулы и рассмотрим решение задачи на вычисление площади треугольника.
Начертим треугольник АВС, из точки С проведем перпендикуляр СH к стороне АВ.
Сторону АВ будем называть основанием, а перпендикуляр СН – высотой треугольника.
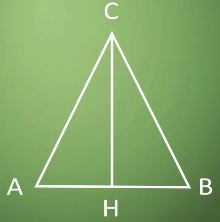
Рассмотрим теорему о площади треугольника:
Площадь треугольника равна половине произведения его основания на высоту.
Докажем это утверждение.
Дан треугольник АВС, АВ – основание, СН – высота.
Нужно доказать:
![]()
Доказательство:
Достроим треугольник АВС до параллелограмма АВDС.
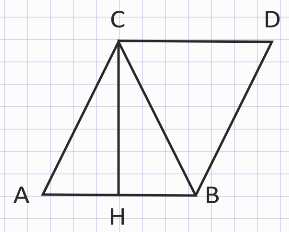
Треугольники АВС и DСВ равны по третьему признаку равенства треугольников (у них сторона ВС является общей, АВ = СD и АС = ВD как противоположные стороны параллелограмма), поэтому площади треугольников АВС и DСВ равны.
Следовательно, площадь треугольника АВС равна половине площади параллелограмма АВDС, а площадь параллелограмма равна произведению его основания на высоту, значит, площадь S треугольника АВС равна 1/2 АВ*СН. Что и требовалось доказать.

У рассмотренной теоремы о площади треугольника есть два следствия.
§ 2 Следствия теоремы о площади треугольника
Одно касается площади прямоугольного треугольника, а второе – отношения площадей треугольников.
Следствие 1:
Площадь прямоугольного треугольника равна половине произведения его катетов.
Таким образом, для вычисления площади прямоугольного треугольника применяют следующую формулу:

Следствие 2:
Если высоты двух треугольников равны, то их площади относятся как основания.
В геометрии есть еще одно утверждение относительно отношения площадей треугольников – это следующая теорема:
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
Решим задачу:
В треугольнике АВС угол С равен 45°, высота АD делит сторону СВ на отрезки СD = 8 см, DВ = 6 см.
Найдите площадь треугольника.
Для вычисления площади треугольника АВС необходимо знать длину высоты АD. Рассмотрим прямоугольный треугольник АСD.
Он равнобедренный, поскольку его углы САD и DСА при основании АС равны. Действительно, угол САD как и угол DСА, он же угол С, тоже равен 45°=180° – (угол АDС + угол С)=180° – (90°+45°).
Так как треугольник АСD равнобедренный, то АD = СD = 8 см.
Площадь S треугольника АВС равна ½ ВС*АD, а ВС = СD + DВ = 8 + 6 = 14 см.
Подставив найденные величины в формулу, получим: площадь треугольника равна 14*8/2=56 см2.
Иногда в геометрии встречаются задачи на вычисление площади треугольника, где даны все три его стороны.
При решении таких задач используют формулу Герона.

Герон Александрийский (I-II вв. н. э.) – древнегреческий инженер, физик, механик, математик, изобретатель.
При вычислении площади равностороннего треугольника используют формулу:
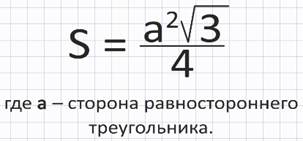
Итак, на этом уроке Вы познакомились с теоремой о площади треугольника и её следствиями, с утверждениями об отношении площадей треугольников, записали формулы нахождения площади треугольников и решили соответствующую задачу.
Список использованной литературы:
- Л.С. Атанасян. Учебник 8 класс.
- Н.Ф. Гаврилова. Поурочные разработки по геометрии 8 класс. – Москва: «Вако», 2005.
- Л.С. Атанасян и др. Методические рекомендации к учебнику. – Москва: «Просвещение», 2001.
- Д.А. Мальцева. Математика 9 класс. ГИА 2014. – Москва: Народное образование, 2013.
- О.В. Белицкая. Геометрия 8 класс. Тесты. – Саратов: «Лицей», 2009.
- С.П. Бабенко, И.С. Маркова. Геометрия 8. Комплексная тетрадь для контроля знаний. – Москва: «Аркти», 2014.
Как найти площадь треугольника – все способы от самых простых до самых сложных
Зависит от того, какой треугольник.

Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.
Если треугольник прямоугольный
То есть один из его углов равен 90 градусам.
Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.

Если он равнобедренный
То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.

Если он равносторонний
То есть все три стороны равны. Ваши действия такие:
- Найдите квадрат стороны – умножьте эту сторону на нее же. Если у вас сторона равна 4, умножьте 4 на 4, будет 16.
- Умножьте полученное значение на корень из 3. Это примерно 1,732050807568877293527.
- Поделите все на 4.

Если известна сторона и высота
Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.

Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.
Если известны две стороны и градус угла между ними
Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:

Если известны длины трех сторон
- Найдите периметр. Для этого сложите все три стороны.
- Найдите полупериметр – разделите периметр на два. Запомните значение.
- Отнимите от полупериметра длину первой стороны. Запомните.
- Отнимите от полупериметра длину второй стороны. Тоже запомните.
- Отнимите от полупериметра длину третьей стороны. И ее запомните.
- Умножьте полупериметр на каждое из этих чисел (разницу с первой, второй и третьей стороной).
- Найдите квадратный корень.

Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.
Если известны три стороны и радиус описанной окружности
Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.

Если известны три стороны и радиус вписанной окружности
Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.
Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.

Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.
Нахождение площади треугольника: формула и примеры
Треугольник – это геометрическая фигура, которая состоит из трех сторон, образованных путем соединения трех точек на плоскости, не принадлежащих одной прямой.
Общие формулы расчета площади треугольника
По основанию и высоте
Площадь (S) треугольника равняется половине произведения его основания и высоты, проведенной к нему.


Формула Герона
Для нахождения площади (S) треугольника необходимо знать длины всех его сторон. Считается она следующим образом:

p – полупериметр треугольника:

Через две стороны и угол между ними
Площадь треугольника (S) равняется половине произведения двух его сторон и синуса угла между ними.


Площадь прямоугольного треугольника
Площадь (S) фигуры равняется половине произведения его катетов.


Площадь равнобедренного треугольника
Площадь (S) рассчитывается по следующей формуле:


Площадь равностороннего треугольника
Чтобы найти площадь правильного треугольника (все стороны фигуры равны), необходимо воспользоваться одной из формул ниже:
Через длину стороны


Через высоту


Примеры задач
Задание 1
Найдите площадь треугольника, если одна из его сторон равна 7 см, а высота, проведенная к ней – 5 см.
Решение:
Используем формулу, в которой участвуют длина стороны и высота:
S = 1/2 ⋅ 7 см ⋅ 5 см = 17,5 см 2 .
Задание 2
Найдите площадь треугольника, стороны которого равны 3, 4 и 5 см.
Решение 1:
Воспользуемся формулой Герона:
Полупериметр (p) = (3 + 4 + 5) / 2 = 6 см.
Решение 2:
Т.к. треугольник со сторонами 3, 4 и 5 – прямоугольный, его площадь можно посчитать по соответствующей формуле:
S = 1/2 ⋅ 3 см ⋅ 4 см = 6 см 2 .
[spoiler title=”источники:”]
[/spoiler]
Геометрия. 8 класс
Выведем формулу для вычисления площади треугольника и следствия из неё.
Одну из сторон треугольника будем называть основанием. Например, сторону AC. Тогда высотой треугольника будем считать ту, которая проведена к основанию.
Достроим треугольник ABC до параллелограмма. Площадь параллелограмма равна сумме площадей треугольников ABC и BCD.
SABC = 1/2 SABCD
SABC = 1/2 AB ∙ BC, но AB и BC – ab, поэтому
SABC = 1/2 ab, где a и b – катеты
Это первое следствие из теоремы о площади треугольника.
С другой стороны площадь прямоугольного треугольника равна половине произведения основания на высоту.
Пусть основанием является гипотенуза, а за высоту треугольника примем высоту, проведённую к гипотенузе.
SABC = 1/2 ch = 1/2 ab,
h = ab/c
Следствие второе:
Если высоты двух треугольников равны, то их площади относятся как основания.
Действительно, если h1 = h2 = h, то выражения для площадей примут вид
SABC = 1/2 AC ∙ hSA1B1C1 = 1/2A1C1 ∙ h
SABC/SA1B1C1 = (1/2 AC ∙ h)/(1/2 A1C1 ∙ h) = AC/A1C1
Тогда отношение площадей равно отношению оснований треугольников. Что и требовалось доказать.
Второе следствие помогает доказать утверждение:
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
Пусть ∠A = ∠A1, тогда
SABC/SA1B1C1 = (AB ∙ AC)/(A1B1 ∙ A1C1)
Знание формулы для вычисления площади прямоугольного треугольника позволяет вывести формулу для вычисления площади ромба, отличную от формулы площади параллелограмма.
Известно, что диагонали ромба делят его на 4 равных прямоугольных треугольника. Поэтому площади этих треугольников равны. Значит, можно утверждать, что площадь ромба равна четырём площадям треугольника. Проведя дальнейшие рассуждения, получим, что площадь ромба равна половине произведения его диагоналей.
Видеоурок площадь треугольника атанасян
Если Вы не нашли темы для своего учебника, то можете добавить оглавление учебника и получить благодарность от проекта “Инфоурок”.
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
У 76% российских учителей оклад ниже МРОТ
Время чтения: 2 минуты
Минобрнауки подготовит государственный рейтинг университетов
Время чтения: 1 минута
Полный перевод школ на дистанционное обучение не планируется
Время чтения: 1 минута
В Египте нашли древние школьные «тетрадки»
Время чтения: 1 минута
В России могут объявить Десятилетие науки и технологий
Время чтения: 1 минута
Общество «Знание» в 2022 году планирует запустить серию хакатонов и школу лекторов
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Решение задач по теме “Площадь”. 8-й класс
Класс: 8
Презентация к уроку
Загрузить презентацию (592 кБ)
Тип урока: урок применения знаний и умений
Цели урока:
- Повторить формулы для вычисления площадей многоугольников;
- Продолжать совершенствовать навыки решения задач по теме «Площадь»;
- Показать применение формулы Герона в процессе решения задач.
- Развивать логическое мышление, математически грамотную речь.
- Воспитывать дружеские отношения в классе; развивать интерес к математике.
Оборудование: учебник, раздаточный материал с тестом, презентация, экран.
Ход урока
I. Организационный момент
Сообщить тему урока. Сформулировать цели урока.
II. Актуализация знаний учащихся
1) Теоретический тест (Текст у каждого на парте)
Работа выполняется на двух листочках, один из которых сдается учителю на проверку, второй остается ученику для самопроверки, которая будет проведена непосредственно по окончанию работы.
I вариант
1. Выберите верные утверждения:
a) площадь прямоугольника равна произведению двух его сторон;
b) площадь квадрата равна квадрату его сторон;
c) площадь прямоугольника равна удвоенному произведению двух его соседних сторон.
2. Закончите фразу: Площадь ромба равна половине произведения…
b) его стороны и высоты, проведенной к этой стороне;
3. По формуле S = a · ha можно вычислить площадь:
4. Площадь трапеции ABCD с основаниями AB и CD и высотой BH вычисляется по формуле:
b) S = (AB + BC) : 2 · BH;
5. Выберите верное утверждение. Площадь прямоугольного треугольника равна:
a) половине произведения его стороны на какую-либо высоту;
b) половине произведения его катетов;
c) произведение его стороны на проведенную к ней высоту.
6. В треугольниках ABC и MNK ∠B = ∠N. Отношение площадей треугольников ABC и MNK равно:

7. В треугольниках MNK и POS высоты NE и OT равны. Тогда SMNK : SPOS = .
II вариант
1. Выберите верные утверждения:
a) площадь квадрата равна произведению его сторон;
b) площадь прямоугольника равна произведению его противолежащих сторон;
c) площадь прямоугольника равна произведению двух его соседних сторон.
2. Закончите фразу: Площадь параллелограмма равна произведению…
b) его стороны на высоту, проведенную к этой стороне;
3. По формуле  можно вычислить площадь:
можно вычислить площадь:
4. Площадь трапеции ABCD с основаниями BC и AD и высотой CH вычисляется по формуле:
b) S = (AB + BC) · CH : 2;
5. Выберите верное утверждение. Площадь треугольника равна:
a) половине произведения его сторон;
b) половине произведения двух его сторон;
c) произведению его стороны на высоту, проведенную к этой стороне.
6. В треугольниках ABC и DEF ∠C = ∠F. Отношение площадей треугольников ABC и DEF равно:

7. В треугольниках DEF и TRQ высоты DA и TB равны. Тогда SDEF : STRQ = .
Ответы к тесту (текст с правильными ответами на экране) (слайды 4 и 5)
1
2
3
4
5
6
7
- Оценка «5» за 7 заданий;
- Оценка «4» за 6 заданий;
- Оценка «3» за 5 заданий.
2) Устное решение задач на готовых чертежах (текст на экране) (слайды 8–10)
Рис. a) Дано: ABCD – параллелограмм, BK = 6 см, KD = 3 см, ∠A = 450. Найти: SABCD.

Рис. b) Дано: ABC – треугольник прямоугольный, BC = 10 см, AB = 8 см. Найти: SABC.

Рис. c) Дано: ABCD – ромб, AC = 10 см, BD = 6 см. Найти: SABCD.

III. Работа в тетрадях (текст на экране) (слайды 12 и 13)
Рис. a) Дано: ABC – треугольник, AB = 14 см. BC = 13 см, AC = 15 см. Найти: SABC.

Рис. b) Дано: ABCD – трапеция, AB = 7 см. BC = 9 см, AD = 12 см, BD = 11 см. Найти: SABCD.

К доске вызывается ученик для решения задачи №504 из учебника.
 Краткое решение:
Краткое решение:
1. Проведем высоту CE. Так как OK⊥AD и CE⊥AD, O – середина AC, то по теореме Фалеса AK = KE = 33 см, тогда DE = 33-12 = 21 см.
2. ΔCED – прямоугольный, по теореме Пифагора: CE 2 = CD 2 – DE 2 ; CE = 20 см.
3. SABCD = AD · CE; SABCD = 900 см 2 .
IV. Рефлексия. Подведение итогов урока
1) Повторить формулы вычисления площадей многоугольников, применяемые на уроке (все формулы вывести на экран) (слайды 15 и 16)
 , где d1 и d2 – диагонали;
, где d1 и d2 – диагонали;
S = ab/2, где a и b – катеты;
S = ((a + b)/2) · h, где a и b – основания, h – высота;
S =  или p = (a + b + c)/2 – формула Герона
или p = (a + b + c)/2 – формула Герона
2) Оценить работу учащихся.
V. Домашнее задание (слайд 17)
В равнобедренной трапеции со взаимно перпендикулярными диагоналями боковая сторона равна 26 см. Высота, проведенная из вершины тупого угла, делит большее основание на отрезки, меньший из которых равен 10 см. Найдите площадь трапеции. (Ответ: 576 см 2 )
Литература:
- Геометрия, 7–9 кл.: учеб. для общеобразоват. учреждений/ Л.С.Атанасян, В.Ф. Бутузов и др. – М.: Просвещение, 2008.
- Геометрия: 8 кл. Рабочая тетрадь/ Л.С. Атанасян, В.Ф. Бутузов и др. – М.: Просвещение, 2008.
- «Изучение геометрии в 7–9 классе». Методические рекомендации/ Л.С.Атанасян, В.Ф. Бутузов и др. – М.: Просвещение, 2008.
- «Дидактические материалы по геометрии. 8 класс»/ Б.Г. Зив, В.М. Мейлер.
[spoiler title=”источники:”]
http://infourok.ru/biblioteka/geometriya/klass-9/uchebnik-602/tema-36383/type-56
http://urok.1sept.ru/articles/599791
[/spoiler]
Прежде, чем
рассматривать вопрос о нахождении площади треугольника, вспомним, что высотой
треугольника называется перпендикуляр, проведённый из вершины треугольника
на противоположную сторону или её продолжение.
Теперь докажем, что
площадь треугольника равна половине произведения длины стороны на высоту,
проведённую к ней.
Доказательство
Пусть –
треугольник.
Докажем, что .
Рассмотрим и
.
,
как
противолеж. стороны ,
–
общая.
по
третьему признаку.
Значит, .
,
,
.
.
.
Что и
требовалось доказать.
Из доказанного
следует, что площадь прямоугольного треугольника равна половине
произведения длин его катетов.
Возьмём некоторый
прямоугольный треугольник ABC.
Катет AC –
это и есть высота, проведённая к стороне BC, которая также является катетом.
А тогда, так как
площадь треугольника равна половине произведения длины стороны на высоту,
проведённую к ней, получаем, что площадь треугольника
, то
есть равняется половине произведения длин катетов рассматриваемого
треугольника.
Также следует, что если
высота одного треугольника равна высоте другого треугольника, то их площади
относятся как длины сторон, к которым проведены высоты.
На рисунке
перпендикуляр BE, проведённый к
прямой AC, является высотой треугольника
ABC и треугольника CBD.
,
.
, то
есть как длины сторон треугольников, к которым проведены высоты.
Теорема. Если угол одного треугольника равен углу другого треугольника, то
площади этих треугольников относятся как произведения сторон, заключающих
равные углы.
Доказательство.
Рассмотрим
треугольники ABC и A1B1C1. Пусть S – площадь
треугольника ABC, а S1 – площадь
треугольника A1B1C1. Углы А и A1 этих треугольников равны.
–
площадь ,
–
площадь .
.
Докажем, что .
,
,
,
.
Таким образом, теорема
доказана.
Закрепим новый
материал на практике.
Задача. Найдите площадь треугольника ,
если длина стороны см,
а высота , проведённая к этой стороне, в два раза её меньше.
Решение.
,
(см).
(см2).
Ответ: см2.
Задача. Вычислите площадь треугольника ,
если высота см,
отрезок см,
а .Решение.
Решение
–
прямоугольный,
так как –
высота.
,
тогда .
Значит, –
равнобедренный, тогда см.
(см).
(см2).
Ответ: см2.
Задача. Найдите длины катетов прямоугольного треугольника, если они относятся
как , а
его площадь равна см2.
Решение.
,
,
,
(см).
(см).
Ответ: см,
см.
Итак, на этом уроке
мы доказали, что площадь треугольника равна половине произведения длины стороны
на высоту, проведённую к ней.
Убедились, что
площадь прямоугольного треугольника равна половине произведения длин его
катетов. А также, что если высота одного треугольника равна высоте другого
треугольника, то их площади относятся как длины сторон, к которым проведены
высоты.
Доказали теорему: если
угол одного треугольника равен углу другого треугольника, то площади этих
треугольников относятся как произведения сторон, заключающих равные углы.
Также мы решили
несколько задач для закрепления изученного материала.
В этом онлайн уроке рассказывается о том, как найти площадь треугольника ABC (прямоугольного, с тупым углом, остроугольного), формула. Начинается обучение с нахождения площади прямоугольного треугольника, т.е. треугольника, в котором один угол равен 90 градусов. Площадь в этом случае вычисляется по очень простой формуле. Она равна половина произведения длин катетов, т.е. двух сторон прилегающих к прямому углу. Справедливость данной формулы объясняется тем, что любой прямоугольный треугольник можно достроить до прямоугольника, добавив точно такой же треугольник. А площадь прямоугольника вычисляется как произведение его длины на ширину, которые являются катетами составляющих его прямоугольных треугольников. Затем в видео уроке объясняется то, как найти площадь треугольника ABC с тупым и с острым углом. Площадь любого треугольника равна половине его основания умноженное на высоту. Эта формула легко доказывается, основываясь на формулу нахождения площади прямоугольного треугольника Видео урок «Как найти площадь треугольника ABC (прямоугольного, с тупым углом, остроугольного), формула» вы можете смотреть онлайн в любое удобное время совершенно бесплатно. Успехов!
- Длительность: 11:02
- Рейтинг: 3.9/21
- 1
- 2
- 3
- 4
- 5
Если у Вас есть качественные видео уроки, которых нет на нашем сайте, то Вы можете добавить их в нашу коллекцию. Для этого Вам необходимо загрузить их на видеохостинг (например, YouTube) и добавить код видео в форму добавления уроков. Возможность добавлять свои материалы доступна только для зарегистрированных пользователей.
