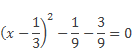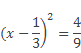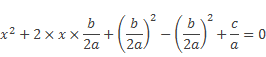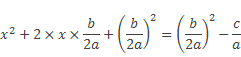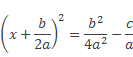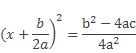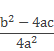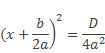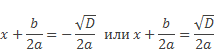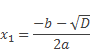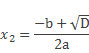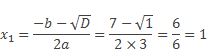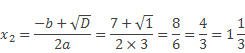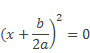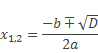Как найти дискриминант видеоурок
Алгебра 8 класс. Как найти дискриминант и как посчитать дискриминант.
Квадратное уравнение, дискриминант, формула корней
Как решать квадратные уравнения через дискриминант. Простое объяснение
Содержание:
- § 1 Формулы сокращенного умножения
- § 2 Решение полного квадратного уравнения
- § 3 Решение неприведенного квадратного уравнения
- § 4 Дискриминант квадратного уравнения
- § 5 Краткие итоги урока
§ 1 Формулы сокращенного умножения
В этом уроке решим квадратное уравнение выделением квадрата двучлена, выведем формулы для нахождения корней полного квадратного уравнения и научимся решать квадратные уравнения по формуле.
Квадратным уравнением называют уравнение вида ax2 + bx + c = 0, где a, b, c –коэффициенты, х – переменная, причём a ≠ 0.
Левая часть квадратного уравнения ax2 + bx + c – это многочлен второй степени. Его называют квадратным трехчленом.
Полное квадратное уравнение, т.е. уравнение, в котором присутствуют все три слагаемых ax2, bx и c, можно решить выделением квадрата двучлена.
Для этого надо знать формулы сокращенного умножения: квадрат суммы и квадрат разности.
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражения плюс квадрат второго выражения.
( a + b)2 = a2 + 2ab + b2
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражения плюс квадрат второго выражения.
(a – b)2 = a2 – 2ab + b2
§ 2 Решение полного квадратного уравнения
Рассмотрим примеры решения полных квадратных уравнений выделением квадрата двучлена. Сначала рассмотрим уравнение, в котором старший коэффициент a равен единице, то есть уравнение является приведенным.
Решим приведенное квадратное уравнение x2 + 6x + 8 = 0.
В квадратном трёхчлене x2 + 6x + 8 необходимо выделить квадрат двучлена. Воспользуемся формулой квадрат суммы.
Представим второй член 6x в виде произведения 2∙х∙3. Тогда для выделения квадрата двучлена к левой части уравнения необходимо прибавить и отнять число 32 = 9. Получаем (x2 + 6x + 9) – 9 + 8 = 0 или (х + 3)2 – 1 = 0.
Перенесем –1 слева направо, изменив знак.
Получим (х + 3)2 = 1.
Отсюда х + 3 = 1 и х + 3 = –1.
Значит, х1 = –2; х2 = –4
§ 3 Решение неприведенного квадратного уравнения
Теперь рассмотрим решение неприведенного квадратного уравнения выделением квадрата двучлена.
Решим уравнение 3х2 – 2х – 1 = 0.
Любое квадратное уравнение можно сделать приведенным.
Для этого надо обе части уравнения разделить на старший коэффициент a.
В нашем примере a = 3.
Разделим обе части уравнения на 3, получим
Это приведенное квадратное уравнение, которое решаем аналогичным предыдущему примеру способом.
Чтобы выделить квадрат двучлена в квадратном трехчлене
воспользуемся формулой квадрат разности.
Второе слагаемое
представим в виде произведения
К левой части уравнения прибавим и вычтем
Получаем
или
или
Отсюда
Значит,
Таким образом, выделением квадрата двучлена можно решить любое полное квадратное уравнение, если сделать его приведенным.
§ 4 Дискриминант квадратного уравнения
Решение квадратных уравнений выделением квадрата двучлена приводит к большим преобразованиям. Чтобы избежать этого, квадратные уравнения решают по формулам. Выведем эти формулы. Для этого к квадратному уравнению в общем виде применим метод выделения квадрата двучлена.
Решим уравнение ax2 + bx + c = 0.
Разделим обе части уравнения на a и получим равносильное приведенное квадратное уравнение
К левой части уравнения
прибавим и вычтем
Получим
или
или
или
Теперь число корней уравнения ax2 + bx + c= 0 зависит от дроби
В частности, от её знака.
Знаменатель 4а2 – положительное число, поэтому знак дроби определяется числителем b2 – 4ac. Это выражение называют дискриминантом квадратного уравнения.
И обозначают буквой D.
При решении квадратного уравнения, в первую очередь, находят дискриминант D по формуле D = b2 – 4ac.
Так как от него зависит число корней уравнения.
Если D>0, то
Отсюда
После преобразований получим
Т.е. уравнение имеет два корня.
Например, решим уравнение 3х2 – 7х + 4 = 0.
Выпишем коэффициенты a = 3, b= –7, с = 4.
Найдем дискриминант D по формуле D = b2 – 4ac.
D= (–7)2 – 4∙3∙4 = 1, D > 0, значит, уравнение имеет два корня
Если D=0, то
Отсюда
Значит, уравнение имеет один корень.
Например, решим уравнение 4х2 – 12х + 9 = 0.
Выпишем коэффициенты a = 4, b= –12, с = 9.
Найдем дискриминант D по формуле D = b2 – 4ac.
D= (–12)2 – 4∙9∙4 = 144 – 144 = 0.
D = 0, значит, уравнение имеет один корень.
Если D < 0, то уравнение корней не имеет.
Например, решим уравнение
2х2 + 7х + 8 = 0.
Выпишем коэффициенты a = 2, b= 7, с = 8.
Найдем дискриминант
D = b2 – 4ac = 72 – 4∙2∙8 = 49 – 64 = –15.
Так как дискриминант меньше нуля, уравнение корней не имеет.
По этим формулам можно решать как полные, так и неполные квадратные уравнения.
§ 5 Краткие итоги урока
Важно запомнить:
При решении квадратного уравнения ax2 + bx + c = 0 по формулам поступают следующим образом:
1.находят дискриминант D по формуле D = b2 – 4ac. Значение дискриминанта зависит от коэффициентов a, b, с;
2.сравнивают дискриминант с нулём;
3.если дискриминант больше нуля, то уравнение ax2 + bx + c = 0 имеет два корня
4.если дискриминант равен нулю, то уравнение имеет один корень
5.если дискриминант меньше нуля, корней нет.
Список использованной литературы:
- Макарычев Ю.Н., Н. Г. Миндюк, Нешков К.И., Суворова С.Б., под редакцией Теляковского С.А. Алгебра: учебн. для 8 кл. общеобразоват. учреждений. – М.: Просвещение, 2013.
- Мордкович А.Г. Алгебра. 8 кл.: В двух частях. Ч.1: Учеб. для общеобразоват. учреждений. – М.: Мнемозина.
- Рурукин А.Н. Поурочные разработки по алгебре: 8 класс.- М.: ВАКО, 2010.
- Алгебра 8 класс: поурочные планы по учебнику Ю. Н. Макарычева, Н. Г. Миндюк, К. И. Нешкова, С. Б. Суворовой / Авт.-сост. Т. Л. Афанасьева, Л. А. Тапилина. -Волгоград: Учитель, 2005.
Как найти дискриминант квадратного уравнения
О чем эта статья:
Понятие квадратного уравнения
Уравнение — это равенство, содержащее переменную, значение которой нужно найти.
Например, х + 8 = 12 — это уравнение, содержащее переменную х.
Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.
Например, если х = 5, то при подстановке в уравнение мы получим:
13 = 12 — противоречие.
Значит, х = 5 не является корнем уравнения.
Если же х = 4, то при подстановке в уравнение мы получим:
12 = 12 — верное равенство.
Значит, х = 4 является корнем уравнения.
Решить уравнение — значит найти все его корни или доказать, что их не существует.
Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Если все коэффициенты в уравнении отличны от нуля, то уравнение называется полным.
Такое уравнение можно решить с помощью формулы дискриминанта.
Понятие дискриминанта
Дискриминант квадратного уравнения — это выражение, равное b 2 − 4ac. Дискриминант в переводе с латинского означает «отличающий» или «различающий» и обозначается буквой D.
Дискриминант — отличный помощник, чтобы понять, сколько в уравнении корней.
Как решать квадратные уравнения через дискриминант
Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:
Определим, чему равны коэффициенты a, b, c.
Вычислим значение дискриминанта по формуле D = b2 − 4ac.
Если дискриминант D 0, то у уравнения две корня, равные
Чтобы запомнить алгоритм решения полных квадратных уравнений и с легкостью его использовать, сохраните себе шпаргалку:
Примеры решения квадратных уравнений с помощью дискриминанта
Пример 1. Решить уравнение: 3x 2 – 4x + 2 = 0.
- Определим коэффициенты: a = 3, b = -4, c = 2.
- Найдем дискриминант: D = b 2 – 4ac = (-4) 2 – 4 * 3 * 2 = 16 – 24 = -8.
Ответ: D 2 – 6x + 9 = 0.
- Определим коэффициенты: a = 1, b = -6, c = 9.
- Найдем дискриминант: D = b 2 – 4ac = (-6) 2 – 4 * 1 * 9 = 36 – 36 = 0.
D = 0, значит уравнение имеет один корень:
Ответ: корень уравнения 3.
Пример 3. Решить уравнение: x 2 – 4x – 5 = 0.
- Определим коэффициенты: a = 1, b = -4, c = -5.
- Найдем дискриминант: D = b 2 – 4ac = (-4) 2 – 4 * 1 * (-5) = 16 + 20 = 36.
D > 0, значит уравнение имеет два корня:
Ответ: два корня x1 = 5, x2 = -1.
Разобраться в решении квадратных уравнений на практике с классным преподавателем можно на курсах по математике в Skysmart.
#115 Урок 1. Квадратные уравнения. Дискриминант. Алгебра 8 класс.
Квадратные уравнения. Какое квадратное уравнение называется полным? Формула дискриминанта и корней полного квадратного уравнения. Уравнения с дробями. Как избавиться от всех знаменателей сразу. Алгебра 8 класс. Примеры с решением и объяснением. Видеоуроки по математике. Устранение пробелов в знаниях. Подготовка к ЗНО ( ВНО ) по математике. Подготовка к ЕГЭ, ДПА ( ГИА ), ОГЭ по математике.
#116 Урок 2. Неполные квадратные уравнения. Решение через дискриминант. Алгебра 8 класс.Математика.
Квадратные уравнения. Какое квадратное уравнение называется полным? Какое квадратное уравнение называется неполным? Формула дискриминанта и корней полного квадратного уравнения. Как решать неполное квадратное уравнение через дискриминант. Алгебра 8 класс. Примеры с решением и объяснением.
#117 Урок 3. Квадратные уравнения. Текстовые задачи. Алгебра 8 класс.
Решение текстовых задач составлением квадратного уравнения. Алгебра 8 класс. Примеры с решением.
- Пример 1: Найдите три последовательных целых числа, если удвоенный квадрат первого из них на 26 больше произведения второго и третьего чисел.
- Пример 2: Найдите четыре последовательных четных числа, если утроенное произведение второго и третьего чисел на 344 больше произведения первого и четвертого.
- Пример 3: Найдите стороны прямоугольника, если их разность равна 23 дм, а диагональ 37 дм.
- Пример 4: Сколько сторон имеет многоугольник, если в нем можно провести 77 диагоналей.
Задачи с объяснением. Видеоуроки по математике. Устранение пробелов в знаниях. Подготовка к ЗНО ( ВНО ) по математике. Подготовка к ЕГЭ, ДПА ( ГИА ), ОГЭ по математике.
#118 Урок 4 Квадратные уравнения. Параметры. При каком значении параметра уравнение имеет 1 корень.
Квадратные уравнения. Параметры. Алгебра 8 класс. Что такое параметр? Понятие параметра в математике. Определение параметра: Если в уравнение или неравенство наряду с неизвестной величиной входят неизвестные, но фиксированные числа, обозначаемые буквами, то они называются параметрами. Пример: 10х2 +4х+b=0; х – переменная; b – параметр; В уравнениях (неравенствах) коэффициенты при неизвестных или свободные члены заданные не конкретными числовыми значениями, а обозначенные буквами называются параметрами. Примеры с решением и объяснением.
- Пример 1: При каком значении а, число 1/3 является корнем уравнения.
- Пример 2: При каком значении b имеет единственный корень уравнение? Условие единственности корня. Видеоуроки по математике. Устранение пробелов в знаниях. Подготовка к ЗНО ( ВНО ) по математике. Подготовка к ЕГЭ, ДПА ( ГИА ), ОГЭ по математике.
#119 Урок 5. Параметры. Решение квадратных уравнений с параметрами. Алгебра 8 класс. Математика.
Параметры. Решение квадратных уравнений с параметрами. Алгебра 8 класс. Квадратные уравнения. Примеры с решением и объяснением.
- Пример 1: Решить квадратное уравнение с параметром, если коэффициент при х2 фиксированное число.
- Пример 2: Решить квадратное уравнение с параметром, если коэффициент при х2 записано с использованием параметра.
#120 Урок 6. Квадратные уравнения с модулем. Алгебра 8 класс. Решить уравнение. Модуль. Математика.
Решение квадратных уравнений с модулем. Алгебра 8 класс. Примеры с решением.
- Пример 1: Решить квадратное уравнение с модулем, раскрыв модуль по определению.
- Пример 2: Решить квадратное уравнение с модулем, раскрыв модуль, используя свойства модуля.
Квадратные уравнения с модулем 8 класс; квадратное уравнение под модулем; квадратные уравнения с модулем примеры; решение квадратных уравнений с модулем 8 класс; квадратные уравнения с модулем примеры решения; решение квадратных уравнений содержащих модуль; как раскрыть модуль квадратного уравнения. Как решать квадратное уравнение с модулем. Как раскрыть модуль, используя его определение. Определение модуля. Свойства модуля. Решить квадратное уравнение. Решить через дискриминант. Сделать проверку. Посторонние корни. Как убрать посторонние корни. Математика. Образование. Подготовка к егэ, егэ математика, видео уроки, подготовка к зно, вно математика. Видео уроки алгебра, алгебра видеоуроки, онлайн урок, математика видео уроки, онлайн урок, инфо урок, огэ, огэ математика. Дистанционное обучение.
#121 Урок 7. Решение квадратных уравнений с использованием свойств функций. Алгебра 8 класс.
Квадратные уравнения. Использование свойств функций для решения квадратных уравнений. Оценка левой и правой частей уравнения. Сумма нескольких неотрицательных функций равна нулю тогда и только тогда, когда все функции одновременно равны нулю. Примеры с решением.
- Пример 1: Решить иррациональное уравнение, приводящееся к квадратному, используя свойства функций.
- Пример 2: Решить уравнение, преобразовав условие по формулам сокращенного умножения и оценив левую и правую части уравнения.
- Пример 3: Решить уравнение с корнем и модулем.
#122 Урок 8. Решение квадратных уравнений с учетом ОДЗ. Область определения. Алгебра 8 класс.
Область определения функции, 4 случая: многочлен, дробь, квадратный корень и квадратные корень в знаменателе. ОДЗ дроби. ОДЗ корня. ОДЗ уравнения. Область определения квадратного корня. Область определения квадратного дроби. Область определения квадратного корня в знаменателе. Что такое область определения. Область определения теория. Область определения, табличка. Примеры с решением. Алгебра 8 класс. Решить квадратное уравнение с учетом ОДЗ. ОДЗ квадратного уравнения; как найти одз в квадратном уравнении; одз корня квадратного уравнения; 2 квадратных уравнения; решение квадратных уравнений; произведение квадратных уравнений; 3 квадратных уравнения. Математика. Образование. Подготовка к егэ, егэ математика, видео уроки, подготовка к зно, вно математика. Видео уроки алгебра, алгебра видеоуроки, онлайн урок, математика видео уроки, онлайн урок, инфо урок, огэ, огэ математика. Дистанционное обучение.
#62 Урок 9. Решение квадратных и кубических уравнений разложением на множители.
Как решить квадратное или кубическое уравнение, разложив его на множители?
- Разложить на множители (вынести общий множитель за скобки, посмотреть формулы, посмотреть способ группировки).
- Приравнять каждый множитель к нулю.
- Решить полученные уравнения.
Формулы сокращенного умножения. Разность квадратов, разность кубов, квадрат разности.Примеры с решением. Решение кубических уравнений. Уравнение четвертой степени. Как решить уравнение?
- Пример 1: Решить кубическое уравнение разложением на множители.
- Пример 2: Решить кубическое уравнение, используя формулы сокращенного умножения.
- Пример 3: Решить кубическое уравнение, используя способ группировки.
- Пример 4: Решить уравнение 4-й степени разложением на множители.
Дискриминант квадратного уравнения
Дискриминант квадратного уравнения — это выражение, находящееся под корнем в формуле нахождения корней квадратного уравнения. Дискриминант обозначается латинской буквой D.
| Вид уравнения | Формула корней | Формула дискриминанта |
|---|---|---|
| ax 2 + bx + c = 0 |  |
b 2 – 4ac |
| ax 2 + 2kx + c = 0 |  |
k 2 – ac |
| x 2 + px + q = 0 |  |
 |
 |
p 2 – 4q |
Все формулы нахождения корней квадратных уравнений можно записать короче с помощью дискриминанта:
| Вид уравнения | Формула |
|---|---|
| ax 2 + bx + c = 0 |  , где D = b 2 – 4ac , где D = b 2 – 4ac |
| ax 2 + 2kx + c = 0 |  , где D = k 2 – ac , где D = k 2 – ac |
| x 2 + px + q = 0 |  , где D = , где D =  |
 , где D = p 2 – 4q , где D = p 2 – 4q |
Дискриминант позволяет определить, имеет ли уравнение корни и сколько их, не решая само уравнение:
- Если дискриминант больше нуля, то уравнение имеет два корня.
- Если дискриминант равен нулю, то уравнение имеет один корень.
- Если дискриминант меньше нуля, то уравнение не имеет корней.
Несмотря на то, что есть несколько формул дискриминанта, чаще всего используют первую:
так как она относится к формуле:

которая является универсальной формулой нахождения корней квадратного уравнения. Данная формула подходит даже для неполных квадратных уравнений.
Решение квадратных уравнений через дискриминант
Для решения квадратного уравнения по формуле можно сначала вычислить дискриминант и сравнить его с нулём. В зависимости от результата, либо искать корни по формуле, либо сделать вывод, что корней нет.
Пример 1. Решить уравнение:
Определим, чему равны коэффициенты:
D = b 2 – 4ac = (-4) 2 – 4 · 3 · 2 = 16 – 24 = -8,
Определим, чему равны коэффициенты:
D = b 2 – 4ac = (-6) 2 – 4 · 1 · 9 = 36 – 36 = 0,
Уравнение имеет всего один корень:
Определим, чему равны коэффициенты:
D = b 2 – 4ac = (-4) 2 – 4 · 1 · (-5) = 16 + 20 = 36,
[spoiler title=”источники:”]
http://math.xfresh.info/index.php/8-klass/algebra-8-klass/38-kvadratnye-uravneniya
http://izamorfix.ru/matematika/algebra/diskriminant.html
[/spoiler]