Видеоурок как найти площадь четырехугольника

Формулы вычисления площади произвольного четырёхугольника

В школьных математических заданиях часто требуется определить площадь четырёхугольника. Все довольно просто, если задан частный случай фигуры — квадрат, ромб, прямоугольник, трапеция, параллелограмм, ромбоид. В случае же произвольного четырёхугольника все несколько сложнее, но также вполне доступно для среднего школьника. Ниже мы изучим различные методы расчётов площади произвольных четырёхугольников, запишем формулы и рассмотрим различные вспомогательные примеры.

Определения и соглашения

В приведённой ниже таблице будут указаны определения и договорённости, которые будут использоваться в дальнейшем во время наших рассуждений.

1. Четырёхугольник – это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.
2. Диагональ — отрезок, соединяющий вершины многоугольника не лежащие на одной стороне (её обозначение – латинская буква d).
3. Площадь фигуры — это численное значение территории, заключённой внутри многоугольника (её обозначение – латинская буква S).
4. Синус угла — это число равное отношению противоположного катета к гипотенузе в прямоугольном треугольнике. (её обозначение – запись sin).
5. Косинус угла — это число равное отношению прилежащего катета к гипотенузе в прямоугольном треугольнике. В дальнейшем в статье для его обозначения будем использовать латинскую запись cos.
6. Описанная окружность — это окружность, которой принадлежат все вершины многоугольника ( её радиуса обозается буквой R).
7. Вписанная окружность — это окружность, которая касается всех сторон многоугольника. В дальнейшем в статье для обозначения её радиуса будем использовать латинскую букву r.
8. Угол между сторонами a и b будем обозначать следующей записью (a,b).

Нахождение площади четырёхугольника различными способами и методами

Узнаем как найти площадь четырёхугольника когда даны его диагонали и образуемый при их пересечении острый угол. Тогда площадь четырёхугольника будет вычисляться по формуле: S = 1/2*d1*d2*sin(d1,d2).

Рассмотрим пример. Пусть d1 = 15 сантиметров, d2 = 12 сантиметров, и угол между ними 30 градусов. Определим S. S = 1/2*15*12*sin30 = 1/2*15*12*1/2 = 45 сантиметров квадратных.

Теперь пусть даны стороны и противолежащие углы четырёхугольника.

Пусть a, b, c, d известные стороны многоугольника; p – его полупериметр. Корень квадратный выражения условимся обозначать как rad (от латинского radical). Формула площади четырёхугольника будет находиться по формуле: S = rad(( p − a ) ( p − b ) ( p − c ) ( p − d ) − a b c d ⋅ c o s^2( (a,b) + (c,d))/2), где p = 1/2*(a + b + c + d).

На первый взгляд, формула кажется очень сложной и вычурной. Однако ничего сложного здесь нет, что мы и докажем, рассмотрев пример. Пусть данные нашего условия следующие: a = 18 миллиметров, b = 23 миллиметра, c = 22 миллиметра, d = 17 миллиметров. Противолежащие углы будут равны (a,b) = 0,5 градуса и (c,d) = 1,5 градуса. Для начала находим полупериметр: p = 1/2*(18 + 23 + 22 + 17) = 1/2*80 = 40 миллиметров.

Теперь найдём квадрат косинуса полусуммы противолежащих углов: c o s^2( (a,b) + (c,d))/2) = c o s^2(0,5 + 1,5)/2 = c o s1*c o s1 = (1/2)*(1/2) = 0,9996.

Подставим полученные данные в нашу формулу, получим: S = rad((40 – 18)*(40 – 23)*(40 – 22)*(40 – 17) – 18*23*22*17*0,97) = rad(22*17*18*23 – 18*23*22*17*1/4) = rad((22*17*18*23*(1 – 0,9996)) = rad(154836*0,0004) = rad62 = 7,875 миллиметра квадратного.

Разберёмся как находить площадь с помощью вписанной и описанной окружностей. При решении задач данной темы имеет смысл сопровождать свои действия вспомогательным рисунком, хотя это требование и не является обязательным.

Если есть вписанная окружность и нужно найти площадь четырёхугольника формула имеет вид:

Снова возьмём на рассмотрение пример: a = 16 метров, b = 30 метров, c = 28 метров, d = 14 метров, r = 6 метров. Подставим аши значения в формулу, получим:

S = ((16 +30 + 28 + 14)/2)*6 = 44*6 = 264 метров квадратных.

Теперь займёмся вариантом когда окружность описана вокруг четырёхугольника. Здесь мы сможем воспользоваться следующей формулой:

S = rad((p − a )*( p − b )*( p − c )*( p − d ), где p равно половине длины периметра. Пускай в нашем случае стороны имеют следующие значения a = 26 дециметров, b = 35 дециметров, c = 39 дециметров, d = 30 дециметров.

Первым делом определим полупериметр, p = (26 + 35 + 39 + 30)/2 = 65 дециметров. Подставим найденное значение в нашу формулу. Получим:

S = rad((65 – 26)*(65 – 35)*(65 – 39)*(65 – 30)) = rad(39*30*26*35) = 1032 (округлённо) дециметров квадратных.

Заключение

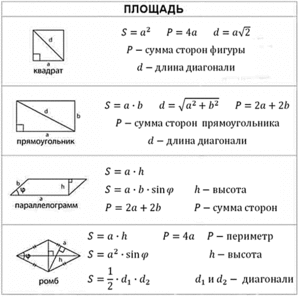
Внимательно изучив все вышеизложенное, можно сделать вывод — определение площади произвольного четырёхугольника с разными сторонами сложнее, чем у них же специальных видов – квадрата, прямоугольника, ромба, трапеции, параллелограмма. Однако внимательно изучив все приведённые методы, можно с лёгкостью решать задачи необходимые для школьников. Сведём все наши формулы в одну таблицу:

1. S = 1/2*d1*d2*sin(d1,d2);
2. S = rad(( p − a )*( p − b )*( p − c )*( p − d ) − a*b*c*d*c o s^2( (a,b) + (c,d))/2), где p = 1/2*(a + b + c + d);
3. S = ((a + b+ c + d)/2)*r

S = rad((p − a )*( p − b )*( p − c )*( p − d ), где p равно половине периметра​.

Таким образом, реально сложной является только формула номер 2, но и она вполне доступна, при условии хорошего понимания данных в статье определений и соглашений.

Видео

Разобраться в этой теме вам поможет видео.

​

Геометрия. Урок 4. Четырехугольники

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

• Определение четырехугольника

• Выпуклые четырехугольники

• Параллелограмм

Определение четырехугольника

Четырехугольником называется фигура, которая состоит из четырех точек (вершин) и четырех отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.

Четырехугольники бывают выпуклые ( A B C D ) и невыпуклые ( A 1 B 1 C 1 D 1 ) .

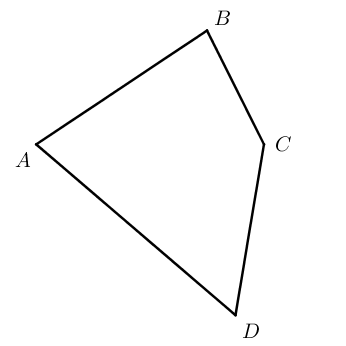
Выпуклые четырехугольники

В задачах ОГЭ встречаются выпуклые четырехугольники, поэтому подробно изучим их.

Смежные стороны – соседние стороны, которые выходят из одной вершины. Пары смежных сторон: A B и A D , A B и B C , B C и C D , C D и A D .

Противолежащие стороны – несмежные стороны (соединяют разные вершины). Пары противолежащих сторон: A B и C D , B C и A D .

Противолежащие вершины – вершины, не являющиеся соседними (лежат друг напротив друга). Пары противолежащих вершин: A и C , B и D .

Диагонали четырехугольника – отрезки, соединяющие противолежащие вершины. A C и B D – диагонали четырехугольника A B C D .

Диагонали выпуклого четырехугольника пересекаются в одной точке.

Площадь произвольного выпуклого четырехугольника можно найти по формуле:

S = 1 2 d 1 d 2 ⋅ sin φ

где d 1 и d 2 – диагонали четырехугольника, φ – угол между диагоналями (острый или тупой – не важно).

Рассмотрим более подробно некоторые виды выпуклых четырехугольников.

Класс параллелограммов : параллелограмм, ромб, прямоугольник, квадрат.

Класс трапеций : произвольная трапеция, прямоугольная трапеция, равнобокая (равнобедренная) трапеция.

Параллелограмм

Параллелограмм – четырехугольник, у которого противолежащие стороны попарно параллельны.

Свойства параллелограмма:

• Противолежащие стороны равны.
• Противоположные углы равны.
• Диагонали точкой пересечения делятся пополам.
• Сумма углов, прилежащих к одной стороне, равна 180 ° .
• Сумма квадратов диагоналей равна сумме квадратов сторон. d 1 2 + d 2 2 = 2 ( a 2 + b 2 )

Площадь параллелограмма можно найти по трём формулам.

Как произведение стороны и высоты, проведенной к ней.

Поскольку стороны имеют разные длины, то высоты, которые к ним проведены, тоже будут иметь разные длины.

Как произведение двух смежных (соседних) сторон на синус угла между ними.

Как полупроизведение диагоналей на синус угла между ними.

Ромб – параллелограмм, у которого все стороны равны.

Свойства ромба:

• Диагонали пересекаются под прямым углом.
• Диагонали являются биссектрисами углов, из которых выходят.
• Сохраняются все свойства параллелограмма.

Площадь ромба можно найти по трём формулам.

Как произведение стороны ромба на высоту ромба.

Как квадрат стороны ромба на синус угла между двумя сторонами.

Как полупроизведение диагоналей ромба.

Прямоугольник

Прямоугольник – это параллелограмм, у которого все углы равны 90 ° .

Свойства прямоугольника:

• Диагонали прямоугольника равны.
• Сохраняются все свойства параллелограмма.

Площадь прямоугольника можно найти по двум формулам:

Как произведение двух смежных (соседних) сторон прямоугольника.

Как полупроизведение диагоналей (так как они обе равны, обозначим их буквой d ) на синус угла между ними.

Квадрат

Квадрат – прямоугольник, у которого все стороны равны.

Свойства квадрата:

• Сохраняет свойства ромба.
• Сохраняет свойства прямоугольника.

Площадь квадрата можно вычислить по двум формулам:

Как квадрат стороны.

Как полупроизведение квадратов диагоналей (диагонали в квадрате равны).

Трапеция

Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие нет.

Стороны, которые параллельны друг другу называются основаниями , другие две стороны называются боковыми сторонами .

B C и A D – основания, A B и C D – боковые стороны трапеции A B C D .

Свойства трапеции:

сумма углов, прилежащих к боковой стороне, равна 180 ° .

Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.

Средняя линия параллельна основаниям. Её длина находится по формуле: m = a + b 2

Площадь трапеции можно найти по двум формулам:

Как полусумму оснований на высоту. Поскольку полусумма оснований есть средняя линия трапеции, можно найти площадь трапеции как произведение средней линии на высоту.

Как полупроизведение диагоналей на синус угла между ними.

Виды трапеций

Прямоугольная трапеция – трапеция, у которой два угла прямые.

Равнобокая (равнобедренная) трапеция – трапеция, у которой боковые стороны равны.

Свойство равнобокой трапеции: углы при основании равны

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с четырехугольниками

Площади четырёхугольников

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Этот урок будет посвящен изучению площади четырехугольников. Для начала вспомним, что такое четырехугольник, перечислим и повторим его основные свойства. После этого запишем формулу расчета площади четырехугольника по известным значениям его диагоналей, вместе с преподавателем решим задачи по пройденной теме.

[spoiler title=”источники:”]

http://interneturok.ru/lesson/geometry/9-klass/itogovoe-povtorenie-kursa-geometrii-za-79-klassy/ploschadi-chetyryohugolnikov

[/spoiler]

Вопросы
занятия:

·  вывести
формулы для вычисления площадей различных четырёхугольников.

Материал
урока

Наряду с понятием длины, понятие
площади является основным в геометрии.

Напомним, что за единицу измерения
площадей принимают квадрат, сторона которого равна единице измерения отрезков.
Т.е. площадь квадрата со стороной, равной одной единице измерения длины, равна
одной квадратной единице. Если же сторона квадрата равна а единиц
измерения длины, то его площадь равна а² квадратных единиц.

Понятно, что равные фигуры имеют
равные площади.

Если же фигура составлена из
нескольких фигур, то её площадь равна сумме площадей составляющих её фигур.

Также напомним, что фигуры, имеющие
равные площади, называют равновеликими.

А начнём мы повторение с площади
прямоугольника.

Площадь
прямоугольника равна произведению его измерений, т.е. произведению длины и
ширины.

Или ещё можно
сказать, что площадь прямоугольника равна произведению его соседних сторон.

Давайте докажем это.

Пусть дан прямоугольник со сторонами
 и
 и
площадью .
Достроим его до квадрата со стороной .

Так как площадь квадрата равна
квадрату его стороны, то площадь построенного квадрата равна .

Но ведь, с другой стороны, площадь
этого квадрата равна сумме площадей .

Так как равны левые части данных
равенств, то можем приравнять и их правые части.

Преобразуем получившееся выражение.
Приведём подобные слагаемые в правой части. Затем перенесём  в
правую часть, а  в
левую. Раскроем скобки в правой части, применив формулу квадрата суммы (при
этом обратите внимание, что перед скобками стоит знак минус). Теперь приведём
подобные слагаемые в правой части. Разделим обе части равенства на – 2. В
результате получим,

То есть площадь прямоугольника со
сторонами  и
 равна
произведению его соседних сторон.

Что и требовалось доказать.

Задача.

Стороны прямоугольника равны 72
метра и 8 метров. Определите сторону равновеликого ему квадрата.

Так как прямоугольник и квадрат
равновелики, то их площади равны.

По формуле площади прямоугольника
имеем, что площадь нашего прямоугольника равна

А значит, и площадь равновеликого
ему квадрата также равна  (м²).

Пусть сторона квадрата равна х.
Так как площадь квадрата равна квадрату его стороны, то получим, что сторона
данного квадрата равна

Следующей вспомним площадь
параллелограмма.

Площадь параллелограмма равна
произведению длины стороны на высоту, проведённую к ней.

Докажем это утверждение.
Пусть  – некоторый параллелограмм.  – высота .
Докажем, что площадь параллелограмма равна .

Проведём к прямой, содержащей
сторону ,
высоту .
Тогда четырёхугольник  является
прямоугольником. Докажем, что .

Рассмотрим прямоугольные
треугольники  и
.
У них гипотенузы  как
противолежащие стороны параллелограмма .
А катеты ,
так как являются высотами проведёнными к одной стороне. Следовательно,
треугольники  по
гипотенузе и катету. Из равенства этих треугольников следует и равенство их
площадей .

Так как трапеция  состоит
из параллелограмма  
и треугольника ,
то .

Также трапеция  является
объединением треугольника  и
прямоугольника .
Следовательно, .

А так как ,
то .

Площадь прямоугольника  равна
.
Тогда и площадь параллелограмма  равна
.

В параллелограмме  стороны
 и
 равны
как противоположные. Значит, площадь параллелограмма  равна
.
То есть площадь параллелограмма равна произведению длины стороны на высоту,
проведённую к ней.

Что и требовалось доказать.

Задача.

Высоты параллелограмма равны  см
и  см,
а угол между ними равен .
Найдите площадь параллелограмма.

Пусть  см,
 см,
.

Напомним, что угол между высотами
параллелограмма, проведёнными из вершины тупого угла, равен острому углу
параллелограмма. Тогда в параллелограмме  угол
.

Рассмотрим треугольник .
Он прямоугольный, так как  высота
по условию. По свойству катета лежащего против угла в 30^о, получаем,
что  (см).

Так как в параллелограмме  стороны
 как противоположные, то площадь параллелограмма равна

Перейдём к площади трапеции.

Площадь трапеции равна
произведению половины суммы её оснований на высоту.

Докажем это утверждение.
Пусть дана трапеция .
 и  – основания, –
высота .

Докажем, что площадь трапеции  равна
.

Проведём диагональ .
Она разбивает трапецию на два треугольника  и
.
Понятно, что площадь трапеции равна сумме площадей этих треугольников .

Напомним, что площадь треугольника
равна .
Тогда площадь треугольника  равна
,
а площадь треугольника  равна
.

Площадь трапеции  равна
сумме площадей этих треугольников.

А тогда имеем, площадь трапеции  равна
.
То есть площадь трапеции равна произведению половины суммы её оснований на
высоту.

Что и требовалось доказать.

Задача.

В прямоугольной трапеции основания
равны  см
и  см,
а большая боковая сторона –  см.
Найдите площадь трапеции.

Пусть дана трапеция .
 перпендикулярно
,
,
 и
.

Проведём высоту .
Получим прямоугольник .
По свойству сторон прямоугольника имеем ,
 см.

Рассмотрим треугольник .
Он прямоугольный, так как  высота
по построению.  в
по условию.  (см).
Тогда по теореме Пифагора можем выразить сторону .

А тогда подставляя все известные данные
в формулу площади трапеции, получим, что площадь нашей трапеции равна  (см²).

И последней вспомним площадь
ромба.

Площадь ромба равна половине
произведения его диагоналей.

Пусть дан ромб .
 и  –
его диагонали.

Докажем, что площадь ромба .

Проведём диагональ .
Она разбивает ромб на два треугольника и
.
Понятно, что площадь ромба равна сумме площадей этих треугольников.

Напомним, что площадь треугольника
равна половине произведения длины стороны треугольника на длину высоту, проведённую
к ней. Напомним, что диагонали ромба взаимно перпендикулярны. Тогда площадь
треугольника  ,
а площадь треугольника  равна
.

Площадь ромба  равна
сумме площадей этих треугольников.

Получаем, что площадь ромба  равна
.
То есть площадь ромба равна половине произведения его диагоналей.

Что и требовалось доказать.

Задача.

Диагонали ромба относятся как .
Найдите площадь ромба, если его периметр равен  см.

Так как диагонали ромба точкой
пересечения делятся пополам, то .

Рассмотрим треугольник .
Он прямоугольный, так как диагонали ромба взаимно перпендикулярны. Напомним,
что стороны ромба равны, а тогда сторона  (см)
. Так как ,
то можем ввести следующие обозначения: .

По теореме Пифагора имеем

А тогда ,
.

А значит, диагонали ромба равны: ,
.

Подставим наши диагонали в формулу
площади ромба. Посчитаем. И получим, что площадь нашего ромба равна

Итоги урока

На этом уроке мы говорили о «четырёхугольниках».
А точнее вспомнили формулы для вычисления их площадей.

Способы нахождения площади четырехугольника. Основные формулы и формула Пика. № 3 ЕГЭ по математике (профиль). Наши бесплатные курсы онлайн https://rabota-ln.ru/registr

Материалы будут полезны не только учащимся школ, лицеев, гимназий, но и педагогам для подготовки к урокам, а также выпускникам прошлых лет, которые решили хорошо подготовиться и сдать единый государственный экзамен по математике.

00:00 Основные формулы для нахождения площадей квадрата, прямоугольника, трапеции, параллелограмма, ромба.

07:08 Способы нахождения площади четырехугольника, применяемые в задачах ЕГЭ №3 профильного уровня.

14:28 Формула Пика для нахождения площади многоугольника.

15:15 Задача № 1 Решение задачи с применением формулы Пика. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см. Ответ дайте в квадратных сантиметрах.

18:03 Задача № 2 Два способа решения задачи на нахождение площади четырехугольника.

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Содержание страницы:

Определение четырехугольника

Четырехугольником называется фигура, которая состоит из четырех точек (вершин) и четырех отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.

Четырехугольники бывают выпуклые  ( A B C D )  и невыпуклые  ( A 1 B 1 C 1 D 1 ) .

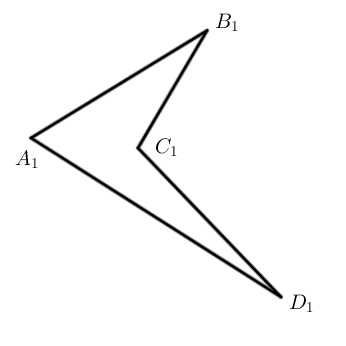
Выпуклые четырехугольники

В задачах ОГЭ встречаются выпуклые четырехугольники, поэтому подробно изучим их.

Смежные стороны – соседние стороны, которые выходят из одной вершины. Пары смежных сторон:  A B  и  A D ,   A B  и  B C ,   B C  и  C D ,   C D  и  A D .

Противолежащие стороны – несмежные стороны (соединяют разные вершины). Пары противолежащих сторон:  A B  и  C D ,   B C  и  A D .

Противолежащие вершины – вершины, не являющиеся соседними (лежат друг напротив друга). Пары противолежащих вершин:  A  и  C ,   B  и  D .

Диагонали четырехугольника – отрезки, соединяющие противолежащие вершины.  A C  и  B D  – диагонали четырехугольника  A B C D .

Диагонали выпуклого четырехугольника пересекаются в одной точке.

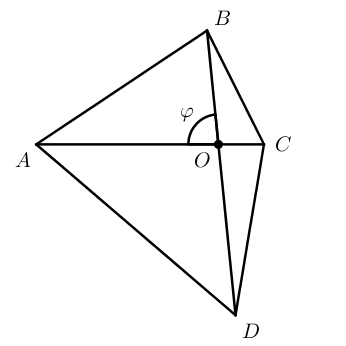
Площадь произвольного выпуклого четырехугольника можно найти по формуле:

S = 1 2 d 1 d 2 ⋅ sin φ

где  d 1  и  d 2  – диагонали четырехугольника,  φ  – угол между диагоналями (острый или тупой – не важно).

Рассмотрим более подробно некоторые виды выпуклых четырехугольников.

Класс параллелограммов: параллелограмм, ромб, прямоугольник, квадрат.

Класс трапеций: произвольная трапеция, прямоугольная трапеция, равнобокая (равнобедренная) трапеция.

Параллелограмм

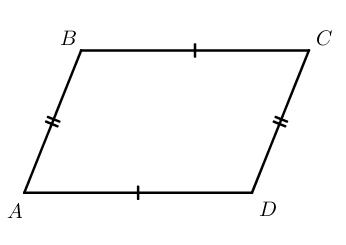
Параллелограмм – четырехугольник, у которого противолежащие стороны попарно параллельны.

Свойства параллелограмма:

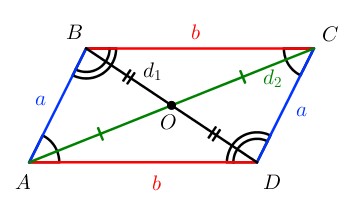
• Противолежащие стороны равны.
• Противоположные углы равны.
• Диагонали точкой пересечения делятся пополам.
• Сумма углов, прилежащих к одной стороне, равна  180 ° .
• Сумма квадратов диагоналей равна сумме квадратов сторон. d 1 2 + d 2 2 = 2 ( a 2 + b 2 )

Площадь параллелограмма можно найти по трём формулам.

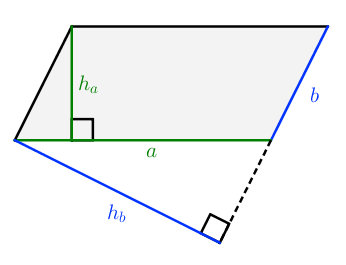
S = a ⋅ h a = b ⋅ h b

Как произведение стороны и высоты, проведенной к ней.

Поскольку стороны имеют разные длины, то высоты, которые к ним проведены, тоже будут иметь разные длины.

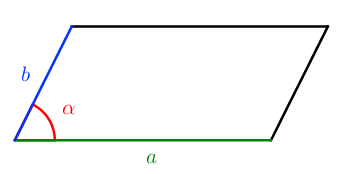
S = a ⋅ b ⋅ sin α

Как произведение двух смежных (соседних) сторон на синус угла между ними.

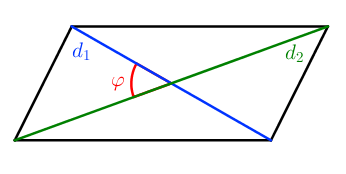
S = 1 2 ⋅ d 1 ⋅ d 2 ⋅ sin φ

Как полупроизведение диагоналей на синус угла между ними.

Ромб

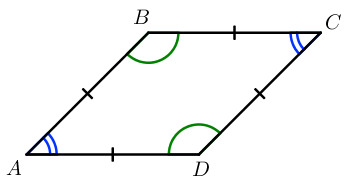
Ромб – параллелограмм, у которого все стороны равны.

Свойства ромба:

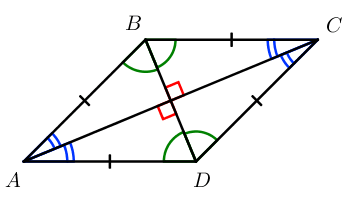
• Диагонали пересекаются под прямым углом.
• Диагонали являются биссектрисами углов, из которых выходят.
• Сохраняются все свойства параллелограмма.

Площадь ромба можно найти по трём формулам.

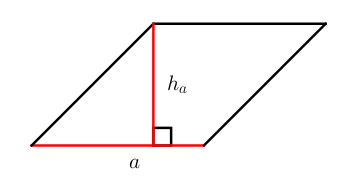
S = a ⋅ h

Как произведение стороны ромба на высоту ромба.

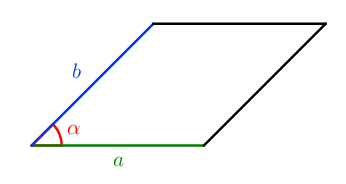
S = a 2 ⋅ sin α

Как квадрат стороны ромба на синус угла между двумя сторонами.

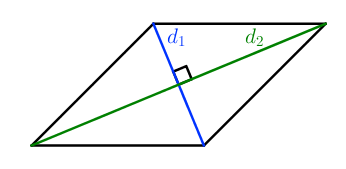
S = 1 2 ⋅ d 1 ⋅ d 2

Как полупроизведение диагоналей ромба.

Прямоугольник

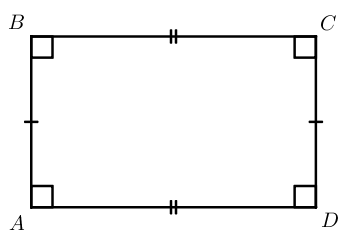
Прямоугольник – это параллелограмм, у которого все углы равны  90 ° .

Свойства прямоугольника:

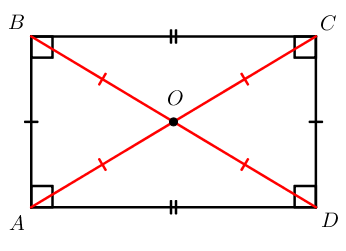
• Диагонали прямоугольника равны.
• Сохраняются все свойства параллелограмма.

Площадь прямоугольника можно найти по двум формулам:

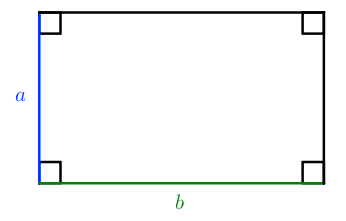
S = a ⋅ b

Как произведение двух смежных (соседних) сторон прямоугольника.

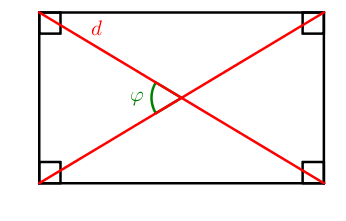
S = 1 2 ⋅ d 2 ⋅ sin φ

Как полупроизведение диагоналей (так как они обе равны, обозначим их буквой d ) на синус угла между ними.

Квадрат

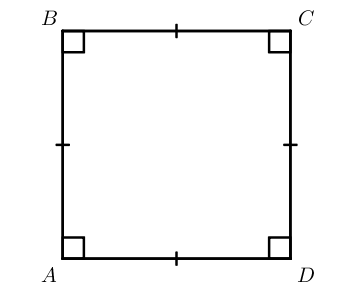
Квадрат – прямоугольник, у которого все стороны равны.

Свойства квадрата:

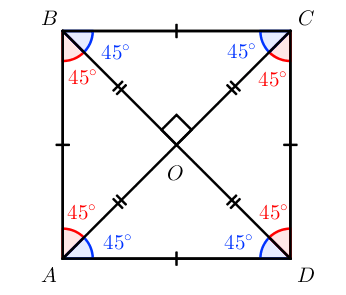
• Сохраняет свойства ромба.
• Сохраняет свойства прямоугольника.

Площадь квадрата можно вычислить по двум формулам:

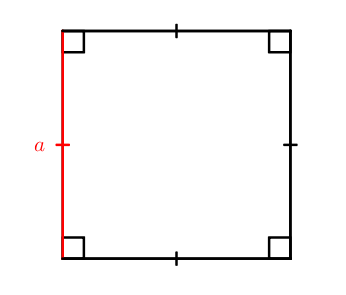
S = a 2

Как квадрат стороны.

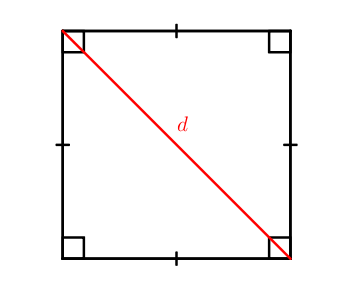
S = d 2 2

Как полупроизведение квадратов диагоналей (диагонали в квадрате равны).

Трапеция

Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие нет.

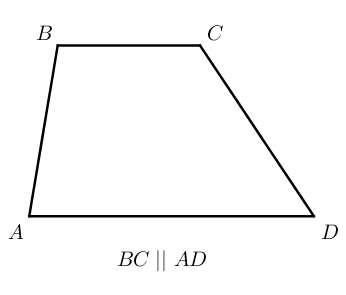
Стороны, которые параллельны друг другу называются основаниями, другие две стороны называются боковыми сторонами.

B C  и  A D  – основания,  A B  и  C D  – боковые стороны трапеции  A B C D .

Свойства трапеции:

сумма углов, прилежащих к боковой стороне, равна  180 ° .

∠ A + ∠ B = 180 °

∠ C + ∠ D = 180 °

Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.

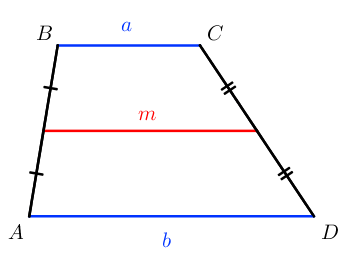
Средняя линия параллельна основаниям. Её длина находится по формуле: m = a + b 2

Площадь трапеции можно найти по двум формулам:

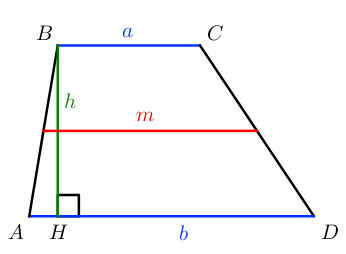
S = a + b 2 ⋅ h = m ⋅ h

Как полусумму оснований на высоту. Поскольку полусумма оснований есть средняя линия трапеции, можно найти площадь трапеции как произведение средней линии на высоту.

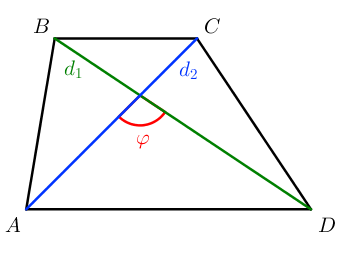
S = 1 2 d 1 ⋅ d 2 ⋅ sin φ

Как полупроизведение диагоналей на синус угла между ними.

Виды трапеций

Прямоугольная трапеция – трапеция, у которой два угла прямые.

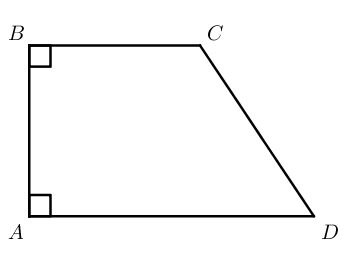
Равнобокая (равнобедренная) трапеция – трапеция, у которой боковые стороны равны.

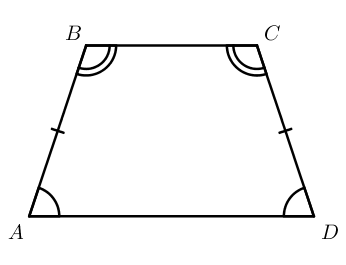
Свойство равнобокой трапеции: углы при основании равны

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с четырехугольниками

Скачать домашнее задание к уроку 4.