Содержание:
- § 1 Понятие прямоугольного параллелепипеда
- § 2 Площадь прямоугольного параллелепипеда
§ 1 Понятие прямоугольного параллелепипеда
В этом уроке Вы познакомитесь с новым понятием – прямоугольный параллелепипед, кроме того научитесь вычислять площадь его поверхности.
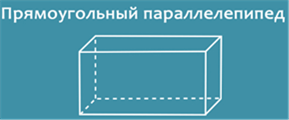
Итак, что же такое прямоугольный параллелепипед? Это такая объемная фигура, которая состоит из 6 прямоугольников, каждый из которых называют гранью прямоугольного параллелепипеда.
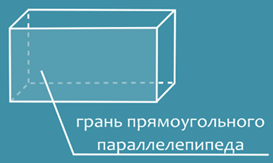
Многие предметы окружающие нас в повседневной жизни имеют форму параллелепипеда. Например, кирпич, спичечный коробок, дом – небоскреб прямоугольной формы, коробка из-под телевизора или системный блок компьютера, все они служат примерами прямоугольного параллелепипеда.
Таким образом:
1.Прямоугольный параллелепипед имеет 6 граней – прямоугольников.
2.Противоположные грани его попарно равны.
3.стороны граней называют ребрами параллелепипеда, а вершины граней – вершинами параллелепипеда. Всего у параллелепипеда имеется 12 ребер и 8 вершин.
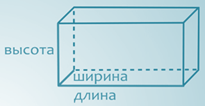
4.Любой прямоугольный параллелепипед имеет три измерения – длину, ширину, высоту. Обычно за них принимают длины трех рёбер прямоугольного параллелепипеда, имеющих общий конец, то есть выходящих из одной вершины.
Так вот, если все три измерения равны, то такой прямоугольный параллелепипед называют кубом. Поэтому, не трудно догадаться, что поверхность куба состоит из 6 равных квадратов, кроме того все 12 рёбер куба также равны.
§ 2 Площадь прямоугольного параллелепипеда
Давайте решим такую задачу. Найдите площадь поверхности прямоугольного параллелепипеда, если его измерения равны 3 см, 6 см и 10 см.
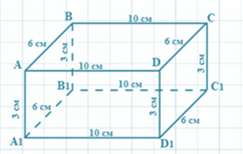
Решение:
![]()
Т.к. прямоугольный параллелепипед имеет 6 граней – прямоугольников, причем противоположные грани его попарно равны, то площадь поверхности прямоугольного параллелепипеда будет равна сумме площадей его 6 граней, при этом площади противоположных друг другу граней будут равны.
Поэтому найдем сначала площади граней, начнем с прямоугольника, у которого стороны равны 3 см и 6 см (помним, что таких граней в параллелепипеде две).
![]()

Для этого 3 умножим на 6, получим 18 квадратных сантиметров. Теперь перейдем к двум другим одинаковым граням – прямоугольникам, со сторонами 3 см и 10 см. Площадь каждой из них равна 3 умножить на 10, будет 30 квадратных сантиметров. Теперь осталось найти площадь каждой из двух последних одинаковых граней со сторонами 6 см и 10 см. Умножим 6 на 10, получим 60 квадратных сантиметров. Значит, площадь всей поверхности прямоугольного параллелепипеда равна 2 умножить на 18 плюс 2 умноженное на 30 плюс 2 умноженное на 60, равно 36 + 60 + 120, получится 216.
Ответ: площадь поверхности прямоугольного параллелепипеда равна двести шестнадцать квадратных сантиметров.
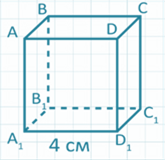
Выполним следующее задание: найти площадь поверхности куба с ребром 4 см.
![]()
Решение: так как у куба 6 граней, каждая из которых является квадратом со стороной 4 см, значит, найдем сначала площадь одной грани. Для этого 4 умножим на 4, или 4 возведем в квадрат, получим 16.
![]()
А затем 16 умножим на 6, будет 96. Ответ: площадь поверхности куба 96 квадратных сантиметров.
Таким образом, на этом уроке Вы познакомились с таким понятием как прямоугольный параллелепипед, его элементами – гранями, ребрами, вершинами. Узнали, что куб – это прямоугольный параллелепипед, у которого все измерения равны. А также научились находить площади поверхностей прямоугольного параллелепипеда и куба.
Список использованной литературы:
- Математика 5 класс. Виленкин Н.Я., Жохов В.И. и др. 31-е изд., стер. – М: 2013.
- Дидактические материалы по математике 5 класс. Автор – Попов М.А. – 2013г.
- Вычисляем без ошибок. Работы с самопроверкой по математике 5-6 классы. Автор – Минаева С.С. – 2014г.
- Дидактические материалы по математике 5 класс. Авторы: Дорофеев Г.В., Кузнецова Л.В. – 2010г.
- Контрольные и самостоятельные работы по математике 5 класс. Авторы – Попов М.А. – 2012г.
- Математика. 5 класс: учеб. для учащихся общеобразоват. учреждений / И. И. Зубарева, А. Г. Мордкович. — 9-е изд., стер. — М.: Мнемозина, 2009. — 270 с.:
Напомним,
что призма, в основании которой лежит параллелограмм, называется параллелепипедом.
Стороны
параллелограммов называются рёбрами параллелепипеда, а их вершины – вершинами
параллелепипеда. Две грани параллелепипеда называются противолежащими,
если они не имеют общего ребра.
Например,
грани и
–
противолежащие.
Грани,
имеющие общее ребро, называются смежными. Например, грани и
–
смежные, ребро у
них общее.
Иногда
какие-нибудь две противолежащие грани параллелепипеда выделяются и называются основаниями,
тогда остальные грани – боковыми гранями, а их стороны, соединяющие
вершины оснований параллелепипеда, – его боковыми рёбрами.
В
нашем случае у параллелепипеда грани
и
–
его основания. Остальные же грани являются боковыми гранями.
Две
вершины параллелепипеда, не принадлежащие одной грани, называются противолежащими.
Отрезок, соединяющий, противолежащие вершины, называется диагональю
параллелепипеда. У параллелепипеда всего четыре диагонали.
Объединение
боковых граней называется боковой поверхностью параллелепипеда, а
объединение всех граней называется полной поверхностью параллелепипеда.
Тогда площадью боковой поверхности параллелепипеда называется сумма
площадей его боковых граней.
А
площадью полной поверхности параллелепипеда называется сумма площадей
всех его граней.
Параллелепипед
обладает следующими свойствами:
1.
Противолежащие грани параллелепипеда равны и лежат в параллельных плоскостях.
2.
Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой
пополам.
3.
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его
измерений.
Объём
параллелепипеда равен произведению площади основания на
высоту.
Объём
прямоугольного параллелепипеда равен произведению трёх
его измерений.
Куб
– это прямоугольный параллелепипед, все рёбра которого равны, то есть все грани
которого – равные квадраты.
Диагональ
куба с ребром равна
.
Объём
куба
равен ,
где –
ребро куба.
Основные
моменты мы с вами повторили, а теперь давайте перейдём к практической части
занятия.
Задача
первая. В основании прямого параллелепипеда лежит параллелограмм
с основаниями см
и см
и острым углом .
Боковое ребро параллелепипеда равно см.
Найдите площадь полной поверхности параллелепипеда.
Решение.
Задача
вторая. Все грани параллелепипеда – ромбы с диагоналями см
и см.
Найдите площадь полной поверхности параллелепипеда.
Решение.
Задача
третья. Найдите меньшую диагональ прямого параллелепипеда
высотой см
со сторонами основания см
и см
и углом между ними .
Решение.
Задача
четвёртая. В прямоугольном параллелепипеде ребро
см,
см.
Найдите расстояние между диагональю параллелепипеда и
ребром .
Решение.
Задача
пятая. Две стороны основания параллелепипеда равны см
и см,
угол между ними .
Боковое ребро равно см
и наклонено к основанию под углом .
Найдите объём параллелепипеда.
Решение.
Задача
шестая. Все грани параллелепипеда – ромбы с периметром
равным и
острым углом .
Найдите объём параллелепипеда.
В ответ запишите значение .
Решение.
Войдите в ОК
Войдите в ОК, чтобы видеть больше.
или
Войти через
Войти через VK ID
Войти через Почту
Войти с помощью Google
Войти через Яндекс
Войти через Apple
Популярные видео
11:25
- Скопировать ссылку
23. Прямоугольный параллелепипед. Площадь поверхности прямоугольного параллелепипеда
2 986 просмотров
Математика. 5-й класс
Виртуальная школа «InternetUrok.ru»
Видео канала
Все »
- Скопировать ссылку
12:20
01. Позиционная система счисления
396 просмотров
- Скопировать ссылку
10:58
02. Понятие числа
160 просмотров
- Скопировать ссылку
09:09
03. Отрезок. Длина отрезка. Треугольник
553 просмотра
Похожие видео
- Скопировать ссылку
21:01
13. Уравнения. Решение задач с помощью уравнений
9 737 просмотров
- Скопировать ссылку
15:53
45. Среднее арифметическое
159 просмотров
- Скопировать ссылку
11:20
19. Решение задач на движение
185 просмотров
- Скопировать ссылку
09:45
29. Сравнение обыкновенных дробей
218 просмотров
- Скопировать ссылку
10:54
06. Сравнение натуральных чисел (Богданович Е.М.)
267 просмотров
- Скопировать ссылку
08:20
07. Сравнение натуральных чисел (Терентьева И.Г.)
330 просмотров
- Скопировать ссылку
13:58
36. Сложение и вычитание десятичных дробей
333 просмотра
- Скопировать ссылку
15:57
15. Деление. Деление с остатком
365 просмотров
- Скопировать ссылку
10:18
17. Порядок выполнения действий
371 просмотр
- Скопировать ссылку
12:20
01. Позиционная система счисления
396 просмотров
- Скопировать ссылку
01:39
Площадь Революции-15июня2018
52 314 просмотров
- Скопировать ссылку
04:25
23 апреля 2018
93 544 просмотра
- Скопировать ссылку
00:17
Площадь
13 156 просмотров
Содержание
- § 1 Понятие прямоугольного параллелепипеда
- § 2 Площадь прямоугольного параллелепипеда
- Список использованной литературы:
§ 1 Понятие прямоугольного параллелепипеда
В этом уроке Вы познакомитесь с новым понятием – прямоугольный параллелепипед, кроме того научитесь вычислять площадь его поверхности.

Итак, что же такое прямоугольный параллелепипед? Это такая объемная фигура, которая состоит из 6 прямоугольников, каждый из которых называют гранью прямоугольного параллелепипеда.

Многие предметы окружающие нас в повседневной жизни имеют форму параллелепипеда. Например, кирпич, спичечный коробок, дом – небоскреб прямоугольной формы, коробка из-под телевизора или системный блок компьютера, все они служат примерами прямоугольного параллелепипеда.
Таким образом:
1.Прямоугольный параллелепипед имеет 6 граней – прямоугольников.
2.Противоположные грани его попарно равны.
3.стороны граней называют ребрами параллелепипеда, а вершины граней – вершинами параллелепипеда. Всего у параллелепипеда имеется 12 ребер и 8 вершин.
4.Любой прямоугольный параллелепипед имеет три измерения – длину, ширину, высоту. Обычно за них принимают длины трех рёбер прямоугольного параллелепипеда, имеющих общий конец, то есть выходящих из одной вершины.

Так вот, если все три измерения равны, то такой прямоугольный параллелепипед называют кубом. Поэтому, не трудно догадаться, что поверхность куба состоит из 6 равных квадратов, кроме того все 12 рёбер куба также равны.
§ 2 Площадь прямоугольного параллелепипеда
Давайте решим такую задачу. Найдите площадь поверхности прямоугольного параллелепипеда, если его измерения равны 3 см, 6 см и 10 см.

Решение:
![]()
Т.к. прямоугольный параллелепипед имеет 6 граней – прямоугольников, причем противоположные грани его попарно равны, то площадь поверхности прямоугольного параллелепипеда будет равна сумме площадей его 6 граней, при этом площади противоположных друг другу граней будут равны.
Поэтому найдем сначала площади граней, начнем с прямоугольника, у которого стороны равны 3 см и 6 см (помним, что таких граней в параллелепипеде две).
![]()

Для этого 3 умножим на 6, получим 18 квадратных сантиметров. Теперь перейдем к двум другим одинаковым граням – прямоугольникам, со сторонами 3 см и 10 см. Площадь каждой из них равна 3 умножить на 10, будет 30 квадратных сантиметров. Теперь осталось найти площадь каждой из двух последних одинаковых граней со сторонами 6 см и 10 см. Умножим 6 на 10, получим 60 квадратных сантиметров. Значит, площадь всей поверхности прямоугольного параллелепипеда равна 2 умножить на 18 плюс 2 умноженное на 30 плюс 2 умноженное на 60, равно 36 + 60 + 120, получится 216.
Ответ: площадь поверхности прямоугольного параллелепипеда равна двести шестнадцать квадратных сантиметров.
Выполним следующее задание: найти площадь поверхности куба с ребром 4 см.

![]()
Решение: так как у куба 6 граней, каждая из которых является квадратом со стороной 4 см, значит, найдем сначала площадь одной грани. Для этого 4 умножим на 4, или 4 возведем в квадрат, получим 16.
![]()
А затем 16 умножим на 6, будет 96. Ответ: площадь поверхности куба 96 квадратных сантиметров.
Таким образом, на этом уроке Вы познакомились с таким понятием как прямоугольный параллелепипед, его элементами – гранями, ребрами, вершинами. Узнали, что куб – это прямоугольный параллелепипед, у которого все измерения равны. А также научились находить площади поверхностей прямоугольного параллелепипеда и куба.
Список использованной литературы:
Предыдущая
5 классВидеоурок «Площадь. Формулы площади прямоугольника и квадрата»
Следующая
5 классВидеоурок «Измерение углов. Транспортир.»
В данной публикации мы рассмотрим, как можно вычислить площадь поверхности прямоугольного параллелепипеда и разберем пример решения задачи для закрепления материала.
- Формула вычисления площади
- Пример задачи
Формула вычисления площади
Площадь (S) поверхности прямоугольного параллелепипеда вычисляется следующим образом:
S = 2 (ab + bc + ac)

Формула получена следующим образом:
- Гранями прямоугольного параллелепипеда являются прямоугольники, причем противоположные грани равны между собой:
- два основания: со сторонами a и b;
- четыре боковые грани: со стороной a/b и высотой c.
- Сложив площади всех граней, каждая из которых равна произведению сторон разной длины, получаем: S = ab + ab + bc + bc + ac + ac = 2 (ab + bc + ac).
Пример задачи
Вычислите площадь поверхности прямоугольного параллелепипеда, если известно, что его длина равна 6 см, ширина – 4 см, а высота – 7 см.
Решение:
Воспользуемся формулой выше, подставив в нее известные значения:
S = 2 ⋅ (6 см ⋅ 4 см + 6 см ⋅ 7 см + 4 см ⋅ 7 см) = 188 см2.
