Видеоурок как найти площадь трапеции

Содержание:

§ 1 Площадь трапеции
§ 2 Решение задачи по теме урока

§ 1 Площадь трапеции

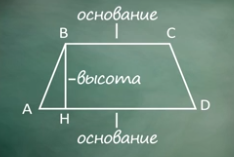
Начертим трапецию АВСD, АD и ВС – основания трапеции, проведем перпендикуляр ВН к основанию АD.

Перпендикуляр, проведенный из любой точки одного из оснований трапеции к прямой, содержащей другое основание, называют высотой трапеции.

ВН – это высота трапеции.

Рассмотрим теорему о площади трапеции.

Теорема:Площадь трапеции равна произведению полусуммы её оснований на высоту.

Докажем это утверждение.

Дано: трапеция АВСD, АD и ВС – основания, ВН – высота.

Доказать: площадь трапеции АВСD будет равна S = ½ (АD + ВС) · ВН.

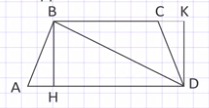
Доказательство: проведем диагональ ВD, она делит трапецию на два треугольника АВD и ВСD. Значит, площадь трапеции АВСD будет равна сумме площадей этих треугольников.

В треугольнике АВD: АD является основанием, а ВH – высотой; в треугольнике ВСD: ВС – основание, проведем высоту DК. Площадь S треугольника АВD = 1/2 АD · ВН; площадь S треугольника ВСD = 1/2 ВС · DК. Так как ВН = DК, то площадь S треугольника ВСD = 1/2 ВС · ВН. Таким образом, площадь S трапеции АВСD = 1/2 АD · ВН + 1/2 ВС · ВН = 1/2 (АD + ВС) · ВН.

Что и требовалось доказать.

§ 2 Решение задачи по теме урока

Решим задачу.

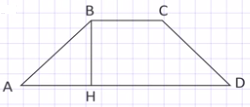
Задача:в равнобедренной трапеции АВСD∠В равен 135°, а высота ВH делит основание АD на отрезки АН = 3 см и НD= 9 см. Найдите площадь трапеции.

Решение: Так как ВН высота трапеции, то ∠В, равный 135°, делится на ∠АВН = 45° и ∠НВС = 90°. ∠А = 45°=∠АВН (т.к. в прямоугольном треугольнике АВН ∠А = 180° – (90° + 45°) = 45°). Следовательно, треугольник АВН равнобедренный и АН = ВН = 3 см. Проведем еще одну высоту нашей трапеции СК, которая разделит отрезок НDна два отрезка НК и КD, НК= НD – КD.

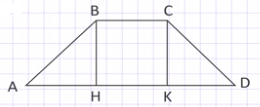
Отрезки АН и КD равные, т.к. по условию трапеция равнобедренная, и равны 3 см. Тогда отрезок НК = 9 – 3 = 6см. Отрезки НК и ВС равны, как противоположные стороны прямоугольника. Таким образом, получаем нижнее основание АD = АН + НD = 3 + 9 = 12 см, а верхнее основание ВС = НК = 6 см, высота же ВН = 3 см. Подставим в формулу для вычисления площади трапеции все эти данные и получим S = ½ (6 + 12)·3 = 27 см2.

Список использованной литературы:

Геометрия. 7-9 классы: учеб. для общеобразоват. организаций / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М.: Просвещение, 2013. – 383 с. : ил.
Н.Ф.Гаврилова. Поурочные разработки по геометрии. 8 класс. – Москва, «Вако», 2005.
Л.С.Атанасян и др. Методические рекомендации к учебнику. – Москва, «Просвещение», 2001.
Д.А.Мальцева. Математика. 9 класс ГИА 2014. – Москва, Народное образование, 2013.
О.В.Белицкая. Геометрия. 8 класс. Тесты. – Саратов, «Лицей», 2009.
С.П.Бабенко, И.С.Маркова. Геометрия 8. Комплексная тетрадь для контроля знаний. – Москва, «Аркти», 2014.

Источник

На этом уроке мы рассмотрим вопрос о вычислении
площади трапеции.

Давайте вспомним одно из свойств площадей: если
многоугольник составлен из нескольких многоугольников, то его площадь равна
сумме площадей этих многоугольников.

Также вспомним, что высотой трапеции
называется перпендикуляр, проведённый из любой точки одного из оснований на
другое основание или его продолжение.

А теперь докажем, что площадь трапеции равна
произведению полусуммы длин её оснований на высоту.

Доказательство

Рассмотрим трапецию .

–
высота.

Докажем, что .

Так как ,

то .

Что и требовалось доказать.

Для закрепления решим несколько задач.

Задача. Найдите площадь
трапеции ,
если см,
см,
см,
а .

Решение

Рассмотрим прямоугольный .

(см).

(см²).

Ответ: см².

Задача. Градусная мера
острого угла прямоугольной трапеции равна ,
а высота, проведённая из вершины тупого угла, делит трапецию на треугольник и
квадрат, площадь которого равна см².
Вычислите площадь трапеции.

Решение.

Пусть ABCD
– прямоугольная трапеция. Градусная мера острого угла C
равна 45º. Высота BE,
проведённая из тупого угла B
делит трапецию на квадрат ABED
и треугольник BCE.

Из условия задачи известно, что см²,
значит, (см).

–
прямоугольный, так как –
высота.

–
равнобедренный.

(см).

,
(см).

(см²).

Ответ: см².

Итак, на этом уроке мы доказали, что площадь
трапеции равна произведению полусуммы длин её оснований на высоту. А также
закрепили это на практике.

Источник

Цифровая библиотека

Интернет-библиотека по школьным предметам от «Онлайн-школы». Библиотека поможет решить домашнее задание, подготовиться к контрольной и вспомнить прошлые темы.

Например: формулы сокращенного умножения

Как поступить
в Онлайн-школу и получить аттестат?

Подробно расскажем о том, как перевестись на дистанционный формат обучения, как устроены онлайн-уроки и учебный процесс, как улучшить успеваемость и повысить мотивацию!

Нажимая на кнопку, я соглашаюсь на обработку

персональных данных