Как можно определить длину высоты ромба

Ромб – это тип многоугольника, у которого все стороны равны между собой. В этом контексте считается важной задачей определение высоты ромба, которая указывает на расстояние между противоположными сторонами многоугольника в случае их параллельности. Чтобы начертить высоту ромба, важно понять и разобраться в теории высоты и смежных сторон, определенных в геометрии. Случайная попытка начертить высоту ромба может привести к неправильным результатам, поэтому важно знать основы теории.

Учитывая различные методы вычисления высоты ромба, мы предоставляем вам возможность легко проработаться с ними и применить их в реальной жизни, на практике. Это пригодится, когда вам нужно будет провести анализ не только ромба, но и других геометрических фигур, таких как треугольник или квадрат.

Конечно, математики уже столетия изучают геометрические фигуры и их свойства, что делает предмет и задачи, связанные с геометрией, матерью всех наук. В этой статье мы попытаемся представить вам один из фундаментальных доступных базовых подходов к определению высоты ромба – и это только кусочек теории, который можно применять и развивать дальше в обучении.

На протяжении статьи мы проделаем путешествие по методам исследования высоты ромба, а также рассмотрим варианты, связанные с разнообразными аспектами геометрии. Вы узнаете, как использовать геометрические свойства и соотношения для вычисления высоты ромба. К концу статьи вы будете в состоянии неоднократно и успешно решать подобные задачи и с большим удовлетворением применять полученные знания и подходы в решении геометрических задач.

Основные понятия в работе с ромбами

Работая с ромбами, важно знать основные понятия и свойства, которые определяют их характеристики и взаимосвязи среди объектов. Это поможет вам легче разрабатывать алгоритмы, решать задачи и подобрать подходящий подход для решения проблемы. Давайте рассмотрим основные понятия и их свойства.

Понятие ромба

Ромб – это четырехугольник с параллельными сторонами одинаковой длины. Важно заметить, что противоположные стороны ромба также являются параллельными, но этим свойством они не обладают только у квадрата и прямоугольника, имеющих разновеликие стороны.

Основные свойства ромбов

• Параллельность сторон: Ромб имеет две пары параллельных сторон.
• Одинаковая длина сторон: Угол между любой парой противоположных сторон ромба равны по длине, что отличает их от прямоугольников.
• Острые углы: Углы при вершинах ромба являются прямыми.

Формулы для вычисления ромбов

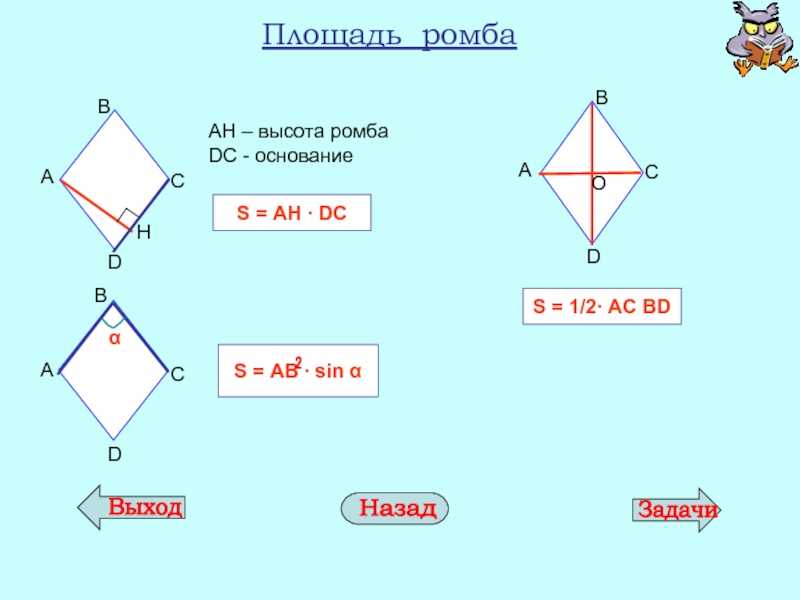
1. Площадь ромба через длину диагонали: d1 и d2 представляют две диагонали ромба, площадь ромба равна половине их произведения: S = 0.5 · d1 · d2.
2. Площадь ромба через стороны: Подобрать два соответствующих угла под arctangent: S = 1/2 · a_1 · a_2·arctg(a_1/a_2)
3. Площадь ромба через длину диагонали и угол: Увеличить ромб до равнобедренного треугольника и применить формулу площади треугольника: S = 1/2 · d · s·sin(2A).

Зная об этих свойствах и используя соответствующие формулы, вы сможете легко работать с ромбами при решении различных задач в математике.

Определение ромба в геометрии

Свойства ромба

1. Все четыре стороны ромба имеют равную длину.
2. Ромб является параллелограмом, ибо пары противоположных сторон являются параллельными.
3. Ромб является равнолобным четырехугольником, поскольку у него все четыре стороны равносторонние.
4. Ромб может быть неравнобедренным, если у него два угла равны, и неравнобедренным, если у него все углы отличаются.
5. Ромб является преобразованием правильного четырехугольника при однозначном вращении любого угла.

Приложения ромба

• Ромбы часто используются в декоративно-прикладном искусстве, архитектуре для украшения объектов.
• Ромбы встречаются в геометрических расчетах, что облегчает решения задач по планиметрии.
• Ромбы играют важную роль в рисовании, дизайн, графика.

Таким образом, вопрос о том, что такое ромб, имеет под собой массу уникальных научных свойств и своих возможностей, активно используемых в разных областях наука и искусства.

Типы ромбов и их отличительные особенности

Прямоугольный ромб

Прямоугольный ромб, также известный как ромб с углами прямыми, обладает двумя уникальными свойствами. Во-первых, все его углы измеряются 90 градусов, поэтому он выглядит как квадрат “на боку”. Во-вторых, попарно противоположные стороны прямоугольного ромба являются взаимно перпендикулярными. Чтобы отличить прямоугольный ромб от других типов ромбов, обратите внимание на углы, которые у него всегда прямые.

Квадрат

Квадрат в геометрии может также быть рассмотрен как ромб с соответствующими свойствами. Квадрат отличается тем, что его все четыре стороны равны по длине и все углы прямые. Чтобы отличить квадрат от других ромбов, обратите внимание на равные стороны и прямые углы в каждом углу квадрата.

Важно отметить, что квадрат является частным случаем прямоугольного ромба и тоже направленных ромбов. Таким образом, если говорить о своеобразном “потоке отцовских ромбов”, то квадрат попадает в эту череду ромбов, наследуя их свойства через свой прямоугольный ромбовидной формы.

Саммы (оскорбительный жест) ромб

Саммы ромб является другим типом ромба, о котором мы должны поговорить. Данный ромб получил своё название в Интернете благодаря своей форме, которая напоминает популярный оскорбительный жест “сукой нач”, широко используемый на Украине. В отличие от предыдущих типов ромбов, у зиксоидного ромба все стороны являются параллельными, и углы также параллельны. Таким образом, все стороны и углы ромба имеют одинаковую длину. Если хотите отличить зиксоид от других ромбов, обратите внимание на соотношение сторон ромба.

Существуют также другие типы ромбов, такие как овальный ромб, параболический ромб и эллиптический ромб. Однако они редко рассматриваются, поскольку их формы исторически представляют поверхность невозможности размышлений поверхностного анализа выделений ромбом формы. Всё-таки, узнав о характеристиках трёх основных ромбов, будет проще понять другие иногда встречающиеся формы ромбов, которые встречаются на нашем пути изучения геометрии и представленных форм ромбом напоминаний.

Связь между стороной и диагональю ромба

Описание стороны и диагонали ромба

Среди всех четырех четвертей ромба, диагонали являются особенно важная характеристику требуются, так как они разделяют его на треугольники со своими сторонами равной длины и своей должен быть прямой. Ромб имеет две диагонали, которые пересекают друг друга в середине ромба и делят его на четыре треугольники равных размеров.

• Сторона: сторона ромба является расстояние между двумя диагональными противоположными точками на границе. Эти стороны должны быть равны длине до порядка.
• Диагональ: диагонали ромба – это линии, соединяющие две не соседние вершины. Вы должны быть одновременно установлены на диагонали ромба ростка размера уменьшенного в два раза со стороны, отрезок ростка полный диагональ ромба.

Формула для связи стороны и диагонали ромба

Длина стороны, ‘a’, ромбы в связи стороны и диагонали ромба может быть вычислена по следующей формуле:

Площадь ромба = 1/2 * a * d1 (или d2)

где d1 и d2 – длины первого и второго диагонали ромба. Площадь ромба оказывается одинаковой, независимо от того, применяется длина первой (d1) или второй (d 2) диагонали

1. Если известно расстояние стороны и первая диагональ, то длина второй диагонали может быть найдена расчетвлера
2. Если известно расстояние стороны и вторая диагональ, то плоскость расчетвлера между первого и второго диагонали используется для нахождения длины первой диагонали.

Данный признак позволяет вычислить длины стороны и диагонали ромба друг от друга, и это очень важно при решении геометрических задач. Связь между стороной и диагонали имеет важное значение также при анализе триангуляции, проектирования и другого, где ромб может быть использована.

Методы определения высоты ромба

Метод 1: Нахождение площади ромба

Один из способов определить высоту ромба – это найти площадь ромба, используя формулу:

Площадь ромба = (половина от деления произведения диагоналей на 2)

Если известны длины двух диагоналей ромба d1 и d2, то высота может быть найдена как половина произведения их длин, делённое на сторону ромба a:

Высота = (1/2 * (d1 * d2)) / a

Метод 2: Использование сторон и углов ромба

Если известны длины сторон и один угол ромба, составляющего, то высоту можно найти с помощью теоремы тотальности углов:

Сумма углов в ромба равна 2*180 = 360. Таким образом, можно использовать эту теорему для нахождения угла между сторонами, и затем использовать теорему косинусов для нахождения высоты.

Если известен один угол нахождения и одна сторона (например, сторона a и u), то высота может быть определена как:

Высота = a*cos(u)

Метод 3: Использование медиан ромба

Если известны длины сторон ромба, то высоту можно найти с использованием формулы для расчёта длины медианы: медиана – это основание высоты ромба.

Длина медианы в ромба – это среднее арифметическое длины двух соседних сторон ромба:

Длина медианы = (a+b)/2

Данную формулу можно использовать для нахождения высоты ромба, умножив полученное значение на 2.

Метод 4: Использование диагоналей ромба

Если известны длины двух диагоналей ромба, используя теорему Пифагора, можно найти высоту ромба.

Перпендикулярная высота к стороне ромба является прямым углом в девяти прямоугольниках: квадрат, в котором стороны это половина диагонали, а диагональ – высота ромба.

По теореме Пифагора, квадрат на высоте равен сумме квадратов на стороне и диагонали ромба, уменьшенном на квадрат на прощадь двух противоположных углов косинус:

Высота = sqrt(d2+a2+b2- 2*a*b*cos(C))

Использование любых из этих методов может достойно помочь вам в определении высоты ромба, основанных на данных, которые у вас есть.

Алгебраические методы

Основной алгебраический приём:

Для нахождения высоты ромба можно воспользоваться следующей формулой:

высота ромба = (площадь ромба) / (длина диагонали ромба)

Используя эту формулу, вы можете легко найти высоту ромба, если известны площадь и длина одной диагонали ромба.

Геометрические сведения:

Ромб – это четырёхугольник с четырьмя равными сторонами. Каждая сторона прилежащей диагонали равняется диагонали, проведенной к противоположному углу.

Таким образом, высота ромба является участком диагонали, проведенной к противоположному углу. Заметим, что площадь ромба равна половине произведения длин диагоналей: площадь ромба = 1/2 * длина диагонали * длина диагонали.

Построение ромба:

Чтобы построить ромб, начните с квадрата. Затем поверните квадрат на 45 градусов, и вы получите ромб с теми же сторонами. Заметим, что в ромбе все углы равны.

Пример:

Пусть у нас имеется ромб со сторонами равной 10 см, площадь которого равна 80 кв. см. Наш первый шаг – использовать формулу для площади ромба. Изначально площадь ромба 1/2хплощадь квадрата = 80 кв. см, очевидно, что площадь квадрата 160 кв. см. Другими словами, площадь одной диагонали ромба равна площади квадрата с стороной 10 см.

Теперь мы можем основываться на основном методе вычисления высоты ромба: высота ромба = (площадь ромба) / (длина диагонали ромба). Таким образом, высота ромба будет равна (80 кв. см) / (10 см) ≈ 8 см.

В итоге, узнав используемые шаги и алгебраические знания, вы можно легко найти высоту ромба.

Геометрические методы

В геометрии существуют разные методы нахождения высоты ромба, позволяющие решить эту задачу с разной степени формализации. Вот некоторые из них:

Использование теоремы Пифагора

Теорема Пифагора основана на свойстве прямоугольного треугольника, согласно которому квадрат на гипотенузе равен сумме квадратов на катетах. В случае ромба, если известен один из углов и длина противоположной стороны, используется следующая формула:

1. Определим прямоугольный треугольник, лежащий на диагонали ромба, и имеющий прямой угол в вершине, лежащей на этой диагонали.

2. Подставляем в теорему Пифагора длину диагонали ромба, которую вычислили ранее, и одну из его сторон.

3. Решаем полученную квадратную уравнение.

Использование построчной модели ромба

Другой метод основан на пошаговом построении ромба и подсчете высоты по линиям, на которые он разбивает пространство. В большинстве случаев этот подход дает корректный результат.

1. Построим вертикальную прямую, пересекающую оба основания ромба.

2. Определим прямоугольные треугольники на этой прямой и подсчитаем их площадь.

3. Поделим накопленную площадь ромба на количество треугольников, тем самым вычислив высоту каждого.

4. Подсчитаем сумму высот треугольников, что даст нам высоту ромба.

Использование абакуса

Абакус представляет собой древний математический инструмент, аналогичный современной компьютерной памяти. Используя его в геометрии, можно упростить вычисления высоты ромба или других фигур.

1. Определите отрезки на абакусе таким образом, чтобы они представляли стороны ромба.

2. Установить на каждом отрезке кол-во камушков, равное их длинам (1 камушок на единицу длины).

3. Перенесение камушков с одного отрезка на другой создает таблицу сумм площадей треугольников на этих отрезках.

4. Потом перенесение камушков на один отрезок, и добавление к ним один на одном, даёт сумму площадей треугольников и высоту ромба.

Итак, геометрическими методами осуществляется поиск высоты ромба на основе треугольников, угла, размеров и построения предварительных последовательностей. Во многих случаях такое подходу даёт эффективное и быстрое решение задачи.

Практический подход к вычислению высоты

Рассмотрим основные приёмы вычисления высоты ромба:

1. По двум сторонам и углу между ними:

   Высота ромба может быть найдена по известной паре сторон и углу между ними:

   1. Разделим угол на две половинки и найдём синус каждой половинки

      sin(угол/2) (при условии, что оба угла малые, иначе придётся брать косинус и корни со знаком минус).

   2. Возьмём абсциссу (значение вдоль оси X) или ординату (значение вдоль оси Y) точки пересечения медианы и стороны ромба.
   3. Умножьте полученное значение на 2 (если использовали ординату) или на √2 / 2 (если использовали абсциссу).
   4. Умножьте полученный результат на длину соответствующей стороны ромба.
   5. Произведя эти вычисления для двух сторон и двух половин угла, получим нужную высоту.
2. По двум сторонам и диагонали:

   Для вычисления высоты рассмотрим случай, когда известны две стороны ромба и его диагональ.

   1. Найдём как векторы разность двух векторов смежных сторон ромба, затем их скалярное произведение.
   2. Умножим полученное значение на 1/2.
   3. Вычислим квадратичный корень из полученного значения.
   4. Окончательный результат: полученный квадратный корень (вектор) плюс квадратный корень из дистанции между центроидами двух сторон.
3. По стороне и углу при вершине:

   Высоту ромба можно найти если известна сторона ромба и угол при вершине.

   1. Углы можно найти используя формулу синуса или косинуса.
   2. Произведя вычисления, получим расстояние от вершины до линии параллельной стороне.
   3. Повторив процедуру для двух сторон параллельных ключевой стороне, получим необходимый результат.

При создании программного решения следует оптимизировать алгоритм вычисления высот ромба, с учетом точности вычислений и используемой формулы.

Вопрос-ответ:

Как определить высоту ромба, используя длину сторон и углы?

Чтобы найти высоту ромба, вам потребуется использовать формулу, основанную на теореме Пифагора. Вам нужно найти длину диагонали ромба. Затем разделите длину каждой диагонали на квадратный корень из 2. Высоту вы получите таким образом: V = да/корень_из_2, где да – это длина диагонали ромба.

Можно ли найти высоту ромба, зная только одну сторону?

Нет, нельзя. Высоту ромба можно найти только при условии, что вы знаете длину двух сторон ромба и знание угла между ними. Или если у вас есть диагонали ромба, вы можете использовать теорему Пифагора и найти высоту ромба.

Как нарисовать ромб с известной высотой и двумя разными длинами сторон?

Чтобы нарисовать ромб, известными свойствами которого являются высота и две разные длины сторон, необходимо учитывать, что высота ромба всегда параллельна более короткой стороне. Поэтому, чтобы отобразить ромб, следует отрисовать линии соответствующих длин и четыре угла, образующие квадрат. Затем отметить на каждой стороне пол длины высоты ромба. Если разница между длинами сторон ромба небольшая, то это будет выглядеть как флажок, а если разница значительная, то более большой флажок будет “опираться” на меньший. В том случае, если разница между длинами сторон ромба будет очень значительной, нарисовано будет близко к равнобедренному прямоугольнику.

Видео:

Найдите площадь ромба, если его высота равна 2, а острый угол 30°