-
Магнитное поле кругового витка с током.
Согласно
закону Био-Савара-Лапласа, индукция
магнитного поля, создаваемого элементом
тока dl на расстоянии r от него есть
![]()
где
α – угол между элементом тока
![]()
и
радиус-вектором
![]()
,
проведенным из этого элемента в точку
наблюдения; r – расстояние от элемента
тока до точки наблюдения.
В
нашем случае α = π/2, sinα = 1;
![]()
, где а – расстояние, отсчитываемое от
центра витка до рассматриваемой точки
на оси витка. Векторы
![]()
образуют
в этой точке конус с углом раствора при
вершине 2
![]()
=
π – 2β, где β – угол между отрезками а и
r.
Из
соображений симметрии ясно, что
результирующее магнитное поле на оси
витка будет направлено вдоль этой оси,
то есть вклад в него дают только те
составляющие, которые параллельны оси
витка:
![]()
Результирующую
величину индукции магнитного поля B на
оси витка получим, проинтегрировав это
выражение по длине контура от 0 до 2πR:
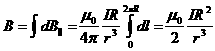
или,
подставив значение r:
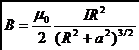
В
частности, при а = 0 находим индукцию
магнитного поля в центре кругового
витка с током:
![]()
Этой
формуле можно придать другой вид,
воспользовавшись определением магнитного
момента витка с током:
![]()
Последнюю
формулу можно записать в векторном виде
(см. рис.9.1):
![]()
.
-
Действие магнитного поля на проводник с током. Закон Ампера.
Магнитное
поле действует с некоторой силой на
любой проводник с током, находящийся
в нем.
Если
проводник, по которому протекает
электрический ток подвесить в магнитном
поле, например, между полюсами магнита,
то магнитное поле будет действовать на
проводник с некоторой силой и отклонять
его.
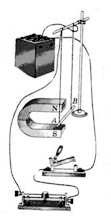
Направление
движения проводника зависит от
направления тока в проводнике и от
расположения полюсов магнита.
Сила,
с которой магнитное поле действует на
проводник с током, называется силой
Ампера.
Французский
физик А. М. Ампер был первым, кто обнаружил
действие магнитного поля на проводник
с током. Правда, источником магнитного
поля в его опытах был не магнит, а другой
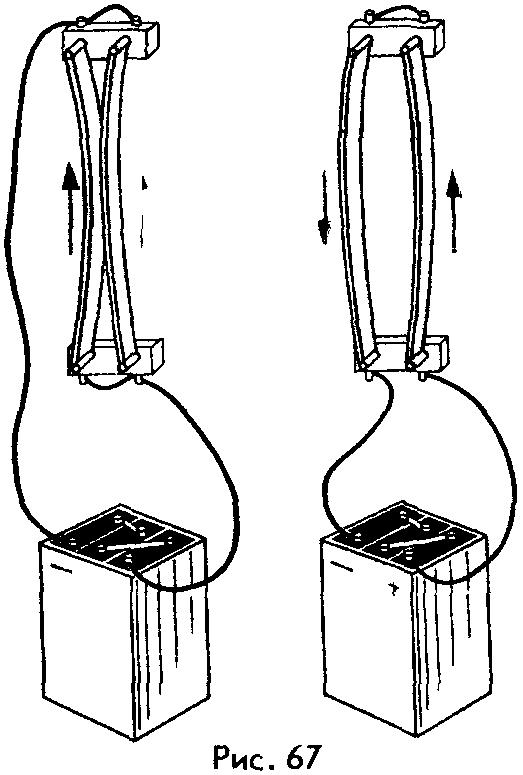
проводник с током. Помещая проводники
с током рядом друг с другом, он обнаружил
магнитное взаимодействие токов (рис.
67) – притяжение параллельных токов и
отталкивание антипараллельных (т. е.
текущих в противоположных направлениях).
В опытах Ампера магнитное поле первого
проводника действовало на второй
проводник, а магнитное поле второго
проводника – на первый. В случае
параллельных токов силы Ампера оказывались
направленными навстречу друг другу и
проводники притягивались; в случае
антипараллельных токов силы Ампера
изменяли свое направление и проводники
отталкивались друг от друга.
Направление
силы Ампера можно определить с помощью
правила левой руки:
если
расположить левую ладонь руки так, чтобы
четыре вытянутых пальца указывали
направление тока в проводнике, а силовые
линии магнитного поля входили в ладонь,
то отставленный большой палец укажет
направление силы, действующей на
проводник с током (рис. 68).
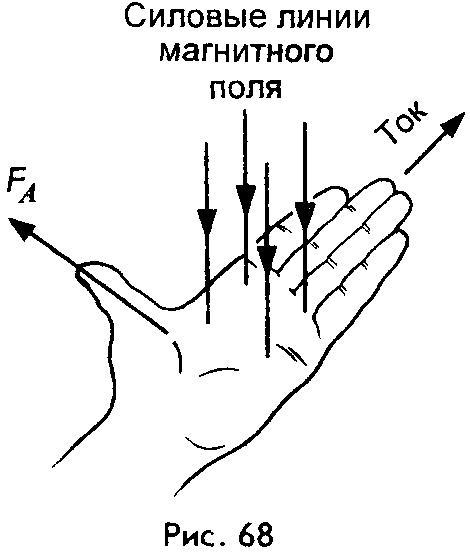
Эта
сила (сила Ампера) всегда перпендикулярна
проводнику, а также силовым линиям
магнитного поля, в котором этот проводник
находится.
Сила
Ампера действует не при любой ориентации
проводника. Если проводник с током
расположить вдоль си
Зако́н
Ампе́ра — закон взаимодействия
электрических токов. Впервые был
установлен Андре Мари Ампером в 1820 для
постоянного тока. Из закона Ампера
следует, что параллельные проводники
с электрическими токами, текущими в
одном направлении, притягиваются, а в
противоположных — отталкиваются.
Законом Ампера называется также закон,
определяющий силу, с которой магнитное
поле действует на малый отрезок проводника
с током. Сила
![]()
,
с которой магнитное поле действует на
элемент объёма
![]()
проводника с током плотности
![]()
,
находящегося в магнитном поле с индукцией
:
![]()
.
![]()
Если
ток течёт по тонкому проводнику, то
![]()
,
где —
![]()
«элемент длины» проводника — вектор,
по модулю равный и совпадающий по
направлению с током. Тогда предыдущее
равенство можно переписать следующим
образом:
Сила
,
с которой магнитное поле действует на
элемент
проводника
с током, находящегося в магнитном поле,
прямо пропорциональна силе тока
![]()
в проводнике и векторному произведению
элемента длины
проводника на магнитную индукцию :
.
![]()
Направление
силы
определяется по правилу вычисления
векторного произведения, которое удобно
запомнить при помощи правила правой
руки.
Модуль
силы Ампера можно найти по формуле:
,
![]()
где
![]()
—
угол между векторами магнитной индукции
и тока.
Сила
![]()
максимальна когда элемент проводника
с током расположен перпендикулярно
линиям магнитной индукции
![]()
![]()
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В школьной физике в качестве источников магнитного поля рассматриваются постоянные магниты и проводники с током. Если постоянные магниты мы уже рассмотрели, то с проводниками давайте разберёмся в данном разделе. Простейшие формы проводников для расчёта магнитных полей:
- бесконечный прямолинейный проводник с током
- круговой виток с током (проводник в форме окружности)
Для каждого из этих проводников можно рассчитать напряжённость магнитного поля в точке.
Итак, движущийся заряд создаёт вокруг себя магнитное поле. Самый простой тип движущегося заряда — это обычный электрический ток. Вопрос только в том, как согнуть проводник:
- бесконечный прямолинейный проводник с током

Рис. 1. Магнитное поле бесконечного проводника
Итак, возьмём бесконечный прямолинейный проводник с током. Слово «бесконечный» в данном случае небольшое приближение. Так для любой точки, находящейся непосредственно вблизи любого линейного проводника, сам проводник «кажется» бесконечным. Пусть по нашему проводнику течёт ток (рис. 1). Прямолинейный проводник с током создаёт вихревое (круговое) магнитное поле вокруг себя. Направление вектора магнитной индукции задаётся правилом буравчика (правилом правой руки). Исходя из этого правила, найдём направление вектора (рис. 2).

Рис. 2. Магнитное поле бесконечного проводника (магнитная индукция)
Для подсчёта модуля вектора магнитной индукции поля вне прямолинейного бесконечного проводника с током можно использовать соотношение (рис. 3):
(1)
- где

Рис. 3. Модуль вектора магнитной индукции бесконечного линейного проводника
3D модели рисунков достаточно сложны для рассмотрения, поэтому введены условные обозначения для направлений векторов/токов в трёхмерном пространстве (рис. 4).

Рис. 4. Схематические отображения векторов
Тогда перерисуем рисунок 3, в случае, если мы смотрим сверху провода (рис. 5.1). В этом случае ток течёт на нас, т.е. из рисунка. И в случае, когда мы смотрим на провод снизу вверх (рис. 5.2). В этом случае ток течёт от нас, т.е. внутрь рисунка.

Рис. 5. Поле проводника (вид сверху)
На рисунке 5 точечной линией обозначено магнитное поле прямолинейного тока (оно круговое). Направление вектора магнитной индукции () определяется правилом буравчика (правилом правой руки).
Правило буравчика для прямолинейного тока: правой рукой обхватываем проводник с током, отогнутый большой палец сонаправляем с током, тогда согнутые 4 пальца показывают направление вектора магнитной индукции.
- круговой виток с током (проводник в форме окружности)
Второй вариант системы, в которой достаточно просто рассчитать модуль вектора магнитной индукции, — это круговой виток с током. Т.е. сам проводник с током представляет собой окружность. По данному проводнику ток может течь как по часовой стрелке (рис. 6.1), так и против часовой (рис. 6.2).

Рис. 6. Круговой виток с током
В целом, магнитное поле такого проводника достаточно сложное, однако для центра витка нахождение модуля вектора магнитной индукции не представляет проблем:
(2)
- где
Немного о — относительной магнитной проницаемости среды. Это параметр, который описывает насколько сама среда воспринимает магнитное поле источника. В целом, это табличная величина.
Правило буравчика для кругового тока: обнимаем правой рукой провод, большой отогнутый палец правой руки направляем по току, тогда загнутые 4 пальца будут указывать направление вектора магнитной индукции.
Важно: для наших систем можно запомнить, что прямолинейный ток создаёт круговое магнитное поле (рис.5), а круговой ток создаёт прямолинейное магнитное поле (рис.6).
Вывод: для поиска модуля вектора магнитной индукции достаточно проанализировать систему в задаче и описать её через модель бесконечного прямолинейного или кругового проводника с током.
Магнитное поле — особая форма материи, посредством которой осуществляется взаимодействие между движущимися электрическими частицами.
Основные свойства магнитного поля
- Магнитное поле порождается электрическим током (движущимися зарядами).
- Магнитное поле обнаруживается по действию на электрический ток (движущиеся заряды).
- Магнитное поле существует независимо от нас, от наших знаний о нем.
Вектор магнитной индукции
Определение
Вектор магнитной индукции — силовая характеристика магнитного поля. Она определяет, с какой силой магнитное поле действует на заряд, движущийся в поле с определенной скоростью. Обозначается как→B. Единица измерения — Тесла (Тл).
За единицу магнитной индукции можно принять магнитную индукцию однородного поля, котором на участок проводника длиной 1 м при силе тока в нем 1 А действует со стороны поля максимальная сила, равна 1 Н. 1 Н/(А∙м) = 1 Тл.
Модуль вектора магнитной индукции — физическая величина, равная отношению максимальной силы, действующей со стороны магнитного поля на отрезок проводника с током, к произведению силы тока и длины проводника:
B=FAmaxIl
За направление вектора магнитной индукции принимается направление от южного полюса S к северному N магнитной стрелки, свободно устанавливающейся в магнитном поле.
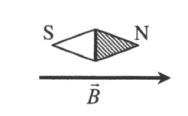
Наглядную картину магнитного поля можно получить, если построить так называемые линии магнитной индукции. Линиями магнитной индукции называют линии, касательные к которым направлены так же, как и вектор магнитной индукции в данной точке поля.
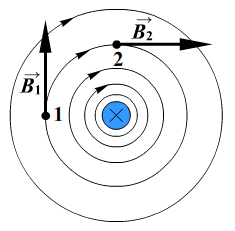
Особенность линий магнитной индукции состоит в том, что они не имеют ни начала, ни конца. Они всегда замкнуты. Поля с замкнутыми силовыми линиями называют вихревыми. Поэтому магнитное поле — вихревое поле.
Замкнутость линий магнитной индукции представляет собой фундаментальное свойство магнитного поля. Оно заключается в том, что магнитное поле не имеет источников. Магнитных зарядов, подобным электрическим, в природе нет.
Напряженность магнитного поля
Определение
Вектор напряженности магнитного поля — характеристика магнитного поля, определяющая густоту силовых линий (линий магнитной индукции). Обозначается как →H. Единица измерения — А/м.
→H=→Bμμ0
μ — магнитная проницаемость среды (у воздуха она равна 1), μ0 — магнитная постоянная, равная 4π·10−7 Гн/м.
Внимание! Направление напряженности всегда совпадает с направлением вектора магнитной индукции: →H↑↑→B.
Направление вектора магнитной индукции и способы его определения
Чтобы определить направление вектора магнитной индукции, нужно:
- Расположить в магнитном поле компас.
- Дождаться, когда магнитная стрелка займет устойчивое положение.
- Принять за направление вектора магнитной индукции направление стрелки компаса «север».
В пространстве между полюсами постоянного магнита вектор магнитной индукции выходит из северного полюса:
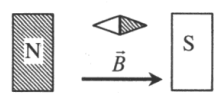
При определении направления вектора магнитной индукции с помощью витка с током следует применять правило буравчика:
При вкручивании острия буравчика вдоль направления тока рукоятка будет вращаться по направлению вектора →B магнитной индукции.
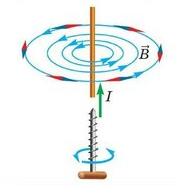
Отсюда следует, что:
- Если по витку ток идет против часовой стрелки, то вектор магнитной индукции →B направлен вверх.
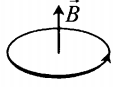
- Если по витку ток идет по часовой стрелке, то вектор магнитной индукции →B направлен вниз.
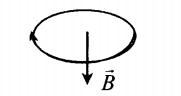
Способы обозначения направлений векторов:
| Вверх | |
| Вниз | |
| Влево | |
| Вправо | |
| На нас перпендикулярно плоскости чертежа |  |
| От нас перпендикулярно плоскости чертежа |  |
Пример №1. На рисунке изображен проводник, по которому течет электрический ток. Направление тока указано стрелкой. Как направлен (вверх, вниз, влево, вправо, от наблюдателя, к наблюдателю) вектор магнитной индукции в точке С?

Если мысленно начать вкручивать острие буравчика по направлению тока, то окажется, что вектор магнитной индукции в точке С будет направлен к нам — к наблюдателю.
Магнитное поле прямолинейного тока
Линии магнитной индукции представляют собой концентрические окружности, лежащие в плоскости, перпендикулярной проводнику. Центр окружностей совпадает с осью проводника.
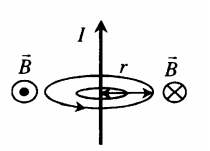
Вид сверху:
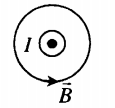
Если ток идет вверх, то силовые линии направлены против часовой стрелки. Если вниз, то они направлены по часовой стрелке. Их направление можно определить с помощью правила буравчика или правила правой руки:
Правило буравчика (правой руки)
Если большой палец правой руки, отклоненный на 90 градусов, направить в сторону тока в проводнике, то остальные 4 пальца покажут направление линий магнитной индукции.
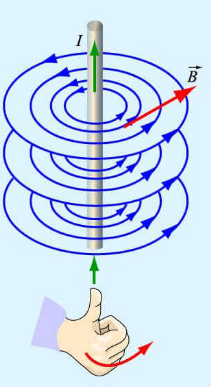
Модуль вектора магнитной индукции на расстоянии r от оси проводника:
B=μμ0I2πr
Модуль напряженности:
H=I2πr
Магнитное поле кругового тока
Силовые линии представляют собой окружности, опоясывающие круговой ток. Вектор магнитной индукции в центре витка направлен вверх, если ток идет против часовой стрелки, и вниз, если по часовой стрелке.
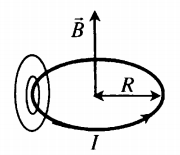
Определить направление силовых линий магнитного поля витка с током можно также с помощью правила правой руки:
Если расположить четыре пальца правой руки по направлению тока в витке, то отклоненный на 90 градусов большой палец, покажет направление вектора магнитной индукции.
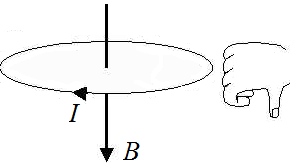
Модуль вектора магнитной индукции в центре витка, радиус которого равен R:
B=μμ0I2R
Модуль напряженности в центре витка:
H=I2R
Пример №2. На рисунке изображен проволочный виток, по которому течет электрический ток в направлении, указанном стрелкой. Виток расположен в вертикальной плоскости. Точка А находится на горизонтальной прямой, проходящей через центр витка. Как направлен (вверх, вниз, влево, вправо) вектор магнитной индукции магнитного поля в точке А?
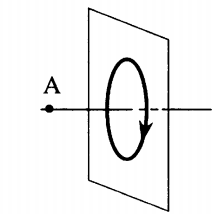
Если мысленно обхватить виток так, чтобы четыре пальца правой руки были бы направлены в сторону тока, то отклоненный на 90 градусов большой палец правой руки показал бы, что вектор магнитной индукции в точке А направлен вправо.
Магнитное поле электромагнита (соленоида)
Определение
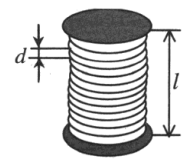
Соленоид — это катушка цилиндрической формы, витки которой намотаны вплотную, а длина значительно больше диаметра.
Число витков в соленоиде N определяется формулой:
N=ld
l — длина соленоида, d — диаметр проволоки.
Линии магнитной индукции являются замкнутыми, причем внутри соленоида они располагаются параллельно друг другу. Поле внутри соленоида однородно.
Если ток по виткам соленоида идет против часовой стрелки, то вектор магнитной индукции →B внутри соленоида направлен вверх, если по часовой стрелке, то вниз. Для определения направления линий магнитной индукции можно воспользоваться правилом правой руки для витка с током.
Модуль вектора магнитной индукции в центральной области соленоида:
B=μμ0INl=μμ0Id
Модуль напряженности магнитного поля в центральной части соленоида:
H=INl=Id
Алгоритм определения полярности электромагнита
- Определить полярность источника.
- Указать на витках электромагнита условное направление тока (от «+» источника к «–»).
- Определить направление вектора магнитной индукции.
- Определить полюса электромагнита. Там, откуда выходят линии магнитной индукции, располагается северный полюс электромагнита (N, или «–». С противоположной стороны — южный (S, или «+»).
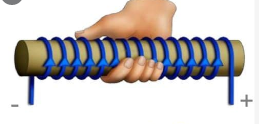
Пример №3. Через соленоид пропускают ток. Определите полюсы катушки.
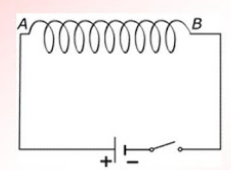
Ток условно течет от положительного полюса источника тока к отрицательному. Следовательно, ток течет по виткам от точки А к точке В. Мысленно обхватив соленоид пальцами правой руки так, чтобы четыре пальца совпадали с направлением тока в витках соленоида, отставим большой палец на угол 90 градусов. Он покажет направление линий магнитной индукции внутри соленоида. Проделав это, увидим, что линии магнитной индукции направлены вправо. Следовательно, они выходят из В, который будет являться северным полюсом. Тогда А будет являться южным полюсом.
Задание EF17530
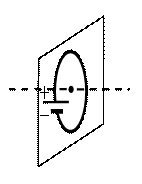 На рисунке изображён круглый проволочный виток, по которому течёт электрический ток. Виток расположен в вертикальной плоскости. В центре витка вектор индукции магнитного поля тока направлен
На рисунке изображён круглый проволочный виток, по которому течёт электрический ток. Виток расположен в вертикальной плоскости. В центре витка вектор индукции магнитного поля тока направлен
Ответ:
а) вертикально вверх в плоскости витка
б) вертикально вниз в плоскости витка
в) вправо перпендикулярно плоскости витка
г) влево перпендикулярно плоскости витка
Алгоритм решения
1.Определить правило, по которому можно определить направление вектора магнитной индукции в данном случае.
2.Применить выбранное правило и определить направление вектора магнитной индукции относительно рисунка.
Решение
По условию задачи мы имеем дело с круглым проволочным витком. Поэтому для определения вектора →B магнитной индукции мы будем использовать правило правой руки.
Чтобы применить это правило, нам нужно знать направление течение тока в проводнике. Условно ток течет от положительного полюса источника к отрицательному. Следовательно, на рисунке ток течет по витку в направлении хода часовой стрелки.
Теперь можем применить правило правой руки. Для этого мысленно направим четыре пальца правой руки в направлении тока в проволочном витке. Теперь отставим на 90 градусов большой палец. Он показывает относительно рисунка влево. Это и есть направление вектора магнитной индукции.
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18109
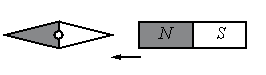 Магнитная стрелка компаса зафиксирована на оси (северный полюс затемнён, см. рисунок). К компасу поднесли сильный постоянный полосовой магнит и освободили стрелку. В каком положении установится стрелка?
Магнитная стрелка компаса зафиксирована на оси (северный полюс затемнён, см. рисунок). К компасу поднесли сильный постоянный полосовой магнит и освободили стрелку. В каком положении установится стрелка?
Ответ:
а) повернётся на 180°
б) повернётся на 90° по часовой стрелке
в) повернётся на 90° против часовой стрелки
г) останется в прежнем положении
Алгоритм решения
- Вспомнить, как взаимодействуют магниты.
- Определить исходное положение полюсов.
- Определить конечное положение полюсов и установить, как изменится положение магнитной стрелки.
Решение
Одноименные полюсы магнитов отталкиваются, а разноименные притягиваются. Изначально южный полюс магнитной стрелки находится справа, а северный — слева. Полосовой магнит подносят к ее южному полюсу северной стороной. Поскольку это разноименные полюса, положение магнитной стрелки не изменится.
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18266
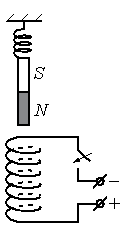 Непосредственно над неподвижно закреплённой проволочной катушкой вдоль её оси на пружине подвешен полосовой магнит (см. рисунок). Куда начнёт двигаться магнит сразу после замыкания ключа? Ответ поясните, указав, какие физические явления и законы Вы использовали для объяснения.
Непосредственно над неподвижно закреплённой проволочной катушкой вдоль её оси на пружине подвешен полосовой магнит (см. рисунок). Куда начнёт двигаться магнит сразу после замыкания ключа? Ответ поясните, указав, какие физические явления и законы Вы использовали для объяснения.
Алгоритм решения
- Определить направление тока в соленоиде.
- Определить полюса соленоида.
- Установить, как будет взаимодействовать соленоид с магнитом.
- Установить, как будет себя вести магнит после замыкания электрической цепи.
Решение
Чтобы определить направление тока в соленоиде, посмотрим на расположение полюсов источника тока. Ток условно направлен от положительного полюса к отрицательному. Следовательно, относительно рисунка ток в витках соленоида направлен по часовой стрелке.
Зная направление тока в соленоиде, можно определить его полюса. Северным будет тот полюс, из которого выходят линии магнитной индукции. Определить их направление поможет правило правой руки для соленоида. Мысленно обхватим соленоид так, чтобы направление четырех пальцев правой руки совпадало с направлением тока в витках соленоида. Теперь отставленный на 90 градусов большой палец покажет направление вектора магнитной индукции. Проделав все манипуляции, получим, что вектор магнитной индукции направлен вниз. Следовательно, внизу соленоида расположен северный полюс, а вверху — южный.
Известно, что одноименные полюса магнитов отталкиваются, а разноименные — притягиваются. Подвешенный полосовой магнит обращен к южному полюсу соленоида северным полюсом. А это значит, что при замыкании электрической цепи он будет растягивать пружину, притягиваясь к соленоиду (двигаться вниз).
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 22.2k
Всем доброго времени суток. В прошлой статье я рассказал о магнитном поле и немного остановился на его параметрах. Данная статья продолжает тему магнитного поля и посвящена такому параметру как магнитная индукция. Для упрощения темы я буду рассказывать о магнитном поле в вакууме, так как различные вещества имеют разные магнитные свойства, и как следствие необходимо учитывать их свойства.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Закон Био – Савара – Лапласа
В результате исследования магнитных полей создаваемых электрическим током, исследователи пришли к таким выводам:
- магнитная индукция, создаваемая электрическим током пропорциональна силе тока;
- магнитная индукция имеет зависимость от формы и размеров проводника, по которому протекает электрический ток;
- магнитная индукция в любой точке магнитного поля зависит от расположения данной точки по отношению к проводнику с током.
Французские учёные Био и Савар, которые пришли к таким выводам обратились к великому математику П. Лапласу для обобщения и вывода основного закона магнитной индукции. Он высказал гипотезу, что индукция в любой точке магнитного поля, создаваемое проводником с током можно представить в виде суммы магнитных индукций элементарных магнитных полей, которые создаются элементарным участком проводника с током. Данная гипотеза и стала законом магнитной индукции, называемого законом Био – Савара – Лапласа. Для рассмотрения данного закона изобразим проводник с током и создаваемую им магнитную индукцию
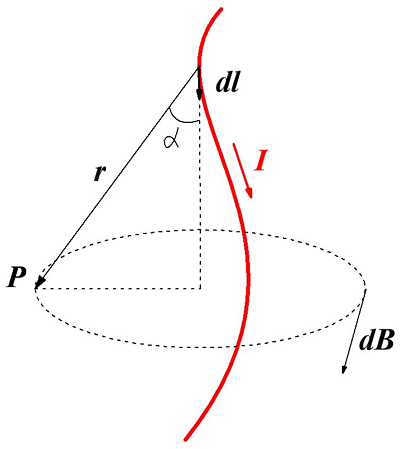
Магнитная индукция dB, создаваемая элементарным участком проводника dl.
Тогда магнитная индукция dB элементарного магнитного поля, которое создается участком проводника dl, с током I в произвольной точке Р будет определяться следующим выражением
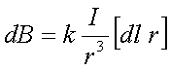
где I – сила тока, протекающая по проводнику,
r – радиус-вектор, проведённый от элемента проводника к точке магнитного поля,
dl – минимальный элемент проводника, который создает индукцию dB,
k – коэффициент пропорциональности, зависящий от системы отсчёта, в СИ k = μ0/(4π)
Так как [dl r] является векторным произведением, тогда итоговое выражение для элементарной магнитной индукции будет выглядеть следующим образом
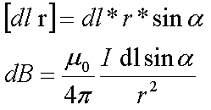
Таким образом, данное выражение позволяет найти магнитную индукцию магнитного поля, которое создается проводником с током произвольной формы и размеров при помощи интегрирования правой части выражения
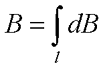
где символ l обозначает, что интегрирование происходит по всей длине проводника.
Магнитная индукция прямолинейного проводника
Как известно простейшее магнитное поле создает прямолинейный проводник, по которому протекает электрический ток. Как я уже говорил в предыдущей статье, силовые линии данного магнитного поля представляют собой концентрические окружности расположенные вокруг проводника.
Магнитная индукция магнитного поля создаваемого прямолинейным проводником с током.
Для определения магнитной индукции В прямого провода в точке Р введем некоторые обозначения. Так как точка Р находится на расстоянии b от провода, то расстояние от любой точки провода до точки Р определяется как r = b/sinα. Тогда наименьшую длину проводника dl можно вычислить из следующего выражения
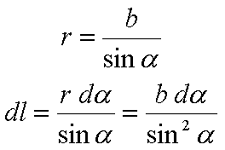
В итоге закон Био – Савара – Лапласа для прямолинейного провода бесконечной длины будет иметь вид
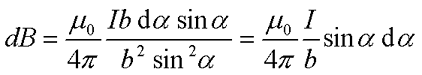
где I – ток, протекающий по проводу,
b – расстояние от центра провода до точки, в которой рассчитывается магнитная индукция.
Теперь просто проинтегрируем получившееся выражение по dα в пределах от 0 до π.
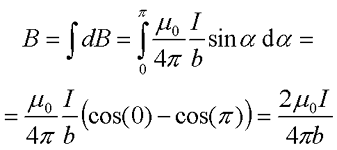
Таким образом, итоговое выражение для магнитной индукции прямолинейного провода бесконечной длины будет иметь вид
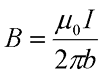
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м,
I – ток, протекающий по проводу,
b – расстояние от центра проводника до точки, в которой измеряется индукция.
Магнитная индукция кольца
Индукция прямого провода имеет небольшое значение и уменьшается при удалении от проводника, поэтому в практических устройствах практически не применяется. Наиболее широко используются магнитные поля созданные проводом, намотанным на какой либо каркас. Поэтому такие поля называются магнитными полями кругового тока. Простейшим таким магнитным поле обладает электрический ток, протекающий по проводнику, который имеет форму окружности радиуса R.
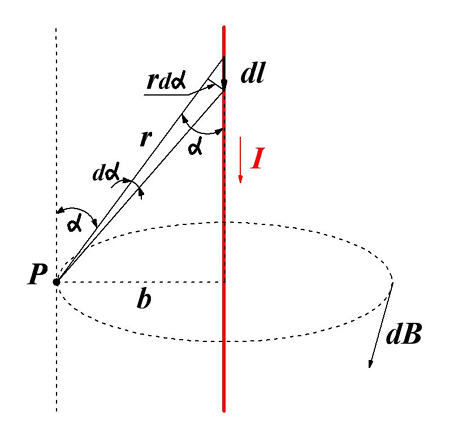
В данном случае практический интерес представляет два случая: магнитное поле в центре окружности и магнитное поле в точке Р, которое лежит на оси окружности. Рассмотрим первый случай.
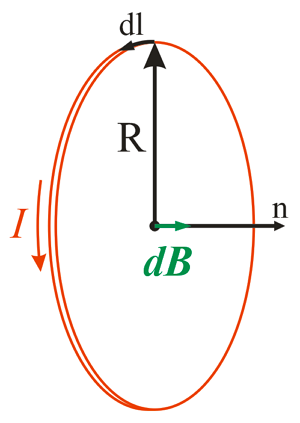
Магнитная индукция в центре кругового тока.
В данном случае каждый элемент тока dl создаёт в центре окружности элементарную магнитную индукцию dB, которая перпендикулярна к плоскости контура, тогда закон Био-Савара-Лапласа будет иметь вид
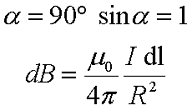
Остается только проинтегрировать полученное выражение по всей длине окружности
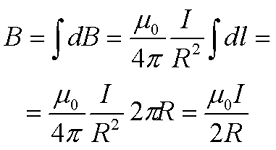
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м,
I – сила тока в проводнике,
R – радиус окружности, в которое свернут проводник.
Рассмотрим второй случай, когда точка, в которой вычисляется магнитная индукция, лежит на прямой х, которая перпендикулярна плоскости ограниченной круговым током.
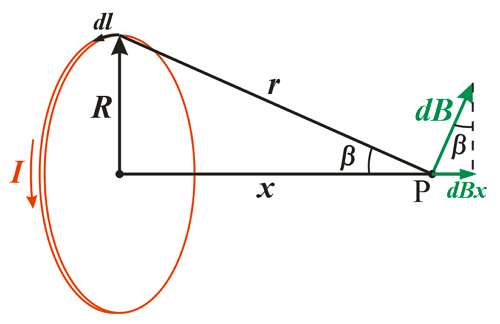
Магнитная индукция в точке, лежащей на оси окружности.
В данном случае индукция в точке Р будет представлять собой сумму элементарных индукций dBX, которые в свою очередь представляет собой проекцию на ось х элементарной индукции dB
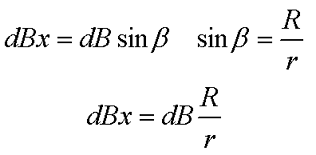
Применив закон Био-Савара-Лапласа вычислим величину магнитной индукции
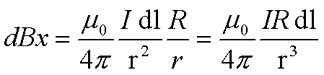
Теперь проинтегрируем данное выражение по всей длине окружности
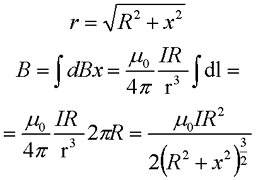
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м,
I – сила тока в проводнике,
R – радиус окружности, в которое свернут проводник,
х – расстояние от точки, в которой вычисляется магнитная индукция, до центра окружности.
Как видно из формулы при х = 0, получившееся выражение переходит в формулу для магнитной индукции в центре кругового тока.
Циркуляция вектора магнитной индукции
Для расчёта магнитной индукции простых магнитных полей достаточно закона Био-Савара-Лапласа. Однако при более сложных магнитных полях, например, магнитное поле соленоида или тороида, количество расчётов и громоздкость формул значительно увеличится. Для упрощения расчётов вводится понятие циркуляции вектора магнитной индукции.
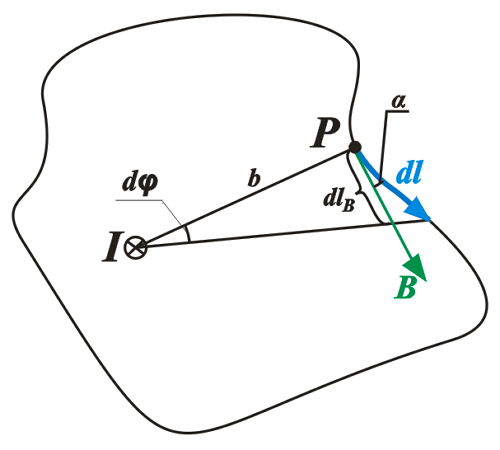
Циркуляция вектора магнитной индукции по произвольному контуру.
Представим некоторый контур l, который перпендикулярный току I. В любой точке Р данного контура, магнитная индукция В направлена по касательной к данному контуру. Тогда произведение векторов dl и В описывается следующим выражением
![]()
Так как угол dφ достаточно мал, то векторов dlВ определяется, как длина дуги
![]()
Таким образом, зная магнитную индукцию прямолинейного проводника в данной точке, можно вывести выражение для циркуляции вектора магнитной индукции
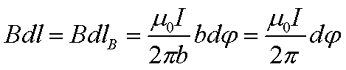
Теперь остаётся проинтегрировать получившееся выражение по всей длине контура
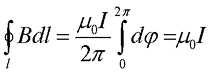
В нашем случае вектор магнитной индукции циркулирует вокруг одного тока, в случае же нескольких токов выражение циркуляции магнитной индукции переходит в закон полного тока, который гласит:
Циркуляция вектора магнитной индукции по замкнутому контуру пропорциональна алгебраической сумме токов, которые охватывает данный контур.
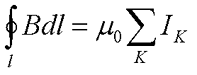
Магнитное поле соленоида и тороида
С помощью закона полного тока и циркуляции вектора магнитной индукции достаточно легко определить магнитную индукцию таких сложных магнитных полей как у соленоида и тороида.
Соленоидом называется цилиндрическая катушка, которая состоит из множества витков проводника, намотанных виток к витку на цилиндрический каркас. Магнитное поле соленоида фактически состоит из множества магнитных полей кругового тока с общей осью, перпендикулярной к плоскости каждого кругового тока.
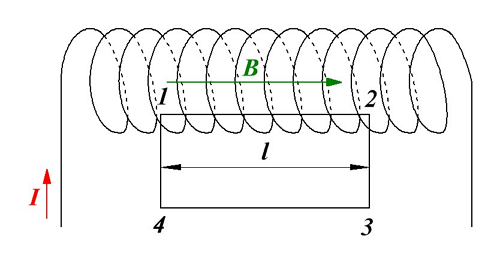
Магнитная индукция соленоида.
Воспользуемся циркуляцией вектора магнитной индукции и представим циркуляцию по прямоугольному контуру 1-2-3-4. Тогда циркуляция вектора магнитной индукции для данного контура будет иметь вид
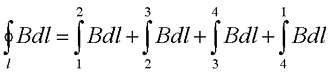
Так как на участках 2-3 и 4-1 вектор магнитной индукции перпендикулярен к контуру, то циркуляция равна нулю. На участке 3-4, который значительно удалён от соленоида, то его так же можно не учитывать. Тогда с учётом закона полного тока магнитная индукция в соленоиде достаточно большой длины будет иметь вид
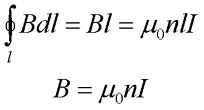
где n – число витков проводника соленоида, которое приходится на единицу длины,
I – ток, протекающий по соленоиду.
Тороид образуется путём намотки проводника на кольцевой каркас. Данная конструкция эквивалентна системе из множества одинаковых круговых токов, центры которых расположены на окружности.
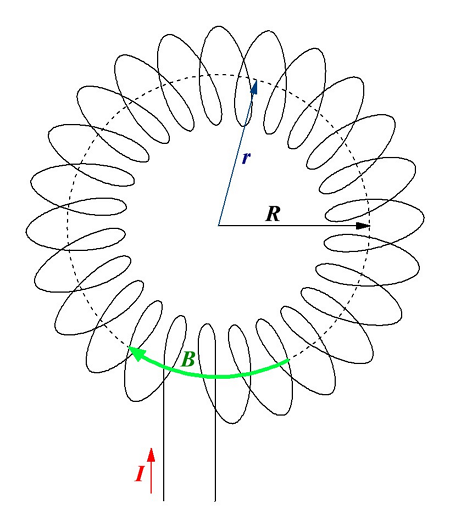
Магнитная индукция тороида.
В качестве примера рассмотрим тороид радиуса R, на который намотано N витков провода. Вокруг каждого витка провода возьмём контур радиуса r, центр данного контура совпадает в центром тороида. Так как вектор магнитной индукции B направлен по касательной к контуру в каждой точке контура, то циркуляция вектора магнитной индукции будет иметь вид
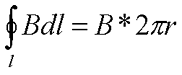
где r – радиус контура магнитной индукции.
Контур проходя внутри тороида охватывает N витков провода с током I, тогда закон полного тока для тороида будет иметь вид
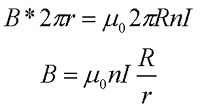
где n – число витков проводника, которое приходится на единицу длины,
r – радиус контура магнитной индукции,
R – радиус тороида.
Таким образом, используя закон полного тока и циркуляцию вектора магнитной индукции можно рассчитать сколь угодно сложное магнитное поле. Однако закон полного тока дает правильные результаты только лишь в вакууме. В случае расчёта магнитной индукции в веществе необходимо учитывать так называемые молекулярные токи. Об этом пойдёт речь в следующей статье.
Индукция магнитного поля в центре и на оси кругового витка с током
Вначале решим более общую задачу нахождения магнитной индукции на оси витка с током. Для этого сделаем рисунок 3.8, на котором изобразим элемент тока 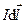 и вектор магнитной индукции
и вектор магнитной индукции  , который он создает на оси кругового контура в некоторой точке
, который он создает на оси кругового контура в некоторой точке  .
.
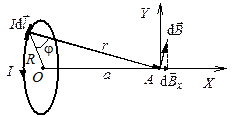
Рис. 3.8 Определение магнитной индукции
на оси кругового витка с током
Вектор магнитной индукции  , создаваемый бесконечно малым элементом контура
, создаваемый бесконечно малым элементом контура 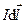 может быть определен с помощью закона Био-Савара-Лапласа (3.10).
может быть определен с помощью закона Био-Савара-Лапласа (3.10).
Как следует из правил векторного произведения, магнитная индукция  будет перпендикулярна плоскости, в которой лежат вектора
будет перпендикулярна плоскости, в которой лежат вектора 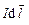 и
и 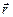 , поэтому модуль вектора
, поэтому модуль вектора  будет равен
будет равен
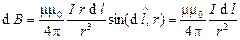 .
.
Для нахождения полной магнитной индукции  от всего контура необходимо векторно сложить
от всего контура необходимо векторно сложить  от всех элементов контура, т. е. фактически сосчитать интеграл по длине кольца
от всех элементов контура, т. е. фактически сосчитать интеграл по длине кольца 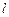
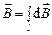 .
.
Данный интеграл можно упростить, если представить  в виде суммы двух составляющих
в виде суммы двух составляющих 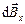 и
и 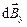
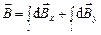
При этом в силу симметрии 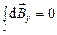 , поэтому результирующий вектор магнитной индукции будет лежать на оси
, поэтому результирующий вектор магнитной индукции будет лежать на оси 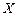 . Следовательно, для нахождения модуля вектора
. Следовательно, для нахождения модуля вектора  нужно сложить проекции всех векторов
нужно сложить проекции всех векторов 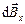 , каждая из которых равна
, каждая из которых равна
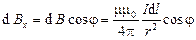 .
.
Учитывая, что 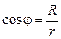 и
и 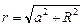 , получим для интеграла следующее выражение
, получим для интеграла следующее выражение
 . (3.18)
. (3.18)
Нетрудно заметить, что вычисление получившегося интеграла даст длину контура, т. е. 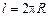 . В итоге суммарная магнитная индукция, создаваемая круговым контуром на оси в точке
. В итоге суммарная магнитная индукция, создаваемая круговым контуром на оси в точке  , равна
, равна
 . (3.19)
. (3.19)
Используя магнитный момент контура, формулу (3.19) можно переписать следующим образом
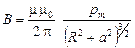 .
.
Теперь отметим, что полученное в общем виде решение (3.19) позволяет проанализировать предельный случай, когда точка  помещена в центре витка. В этом случае
помещена в центре витка. В этом случае 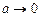 и решение для магнитной индукции поля в центре кольца с током примет вид
и решение для магнитной индукции поля в центре кольца с током примет вид
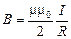 . (3.20)
. (3.20)
Результирующий вектор магнитной индукции (3.19) направлен вдоль оси тока, а его направление связано с направлением тока правилом правого винта (рис. 3.9).
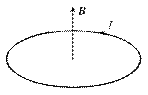
Рис. 3.9 Определение магнитной индукции
в центре кругового витка с током
Индукция магнитного поля в центре дуги окружности
Данная задача может быть решена как частный случай рассмотренной в предыдущем пункте задачи. В этом случае интеграл в формуле (3.18) следует брать не по всей длине окружности, а только по ее дуге l. А также учесть то, что индукция ищется в центре дуги, поэтому 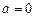 . В результате получим
. В результате получим
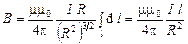 , (3.21)
, (3.21)
где 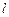 – длина дуги;
– длина дуги;  – радиус дуги.
– радиус дуги.
5 Вектор индукции магнитного поля движущегося в вакууме точечного заряда (без вывода формулы)
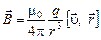 ,
,
где 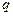 – электрический заряд;
– электрический заряд; 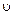 – постоянная нерелятивистская скорость;
– постоянная нерелятивистская скорость; 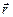 – радиус-вектор, проведенный от заряда к точке наблюдения.
– радиус-вектор, проведенный от заряда к точке наблюдения.
Силы Ампера и Лоренца
Опыты по отклонению рамки с током в магнитном поле показывают, что на всякий проводник с током, помещенный в магнитное поле, действует механическая сила, называемая силой Ампера.
Закон Ампера определяет силу, действующую на проводник с током, помещенный в магнитное поле:
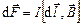 ;
; 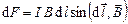 , (3.22)
, (3.22)
где 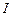 – сила тока;
– сила тока;  – элемент длины провода (вектор
– элемент длины провода (вектор 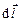 совпадает по направлению с током
совпадает по направлению с током 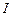 );
); 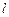 – длина проводника. Сила Ампера перпендикулярна направлению тока и направлению вектора магнитной индукции.
– длина проводника. Сила Ампера перпендикулярна направлению тока и направлению вектора магнитной индукции.
Если прямолинейный проводник длиной 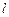 находится в однородном поле, то модуль силы Ампера определяется выражением (рис. 3.10):
находится в однородном поле, то модуль силы Ампера определяется выражением (рис. 3.10):
 . (3.23)
. (3.23)
Сила Ампера всегда направлена перпендикулярно плоскости, содержащей векторы 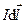 и
и  , а ее направление как результат векторного произведения определяется правилом правого винта: если смотреть вдоль вектора
, а ее направление как результат векторного произведения определяется правилом правого винта: если смотреть вдоль вектора 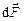 , то поворот от
, то поворот от 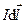 к
к  по кратчайшему пути должен происходить по часовой стрелке.
по кратчайшему пути должен происходить по часовой стрелке.
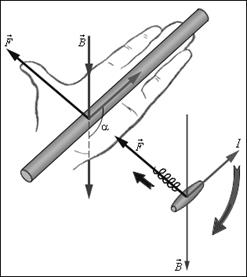
Рис. 3.10 Правило левой руки и правило буравчика для силы Ампера
С другой стороны, для определения направления силы Ампера можно также применить мнемоническоеправило левой руки (рис. 3.10): нужно поместить ладонь так, чтобы силовые линии магнитной индукции  входили в нее, вытянутые пальцы показывали направление тока, тогда отогнутый большой палец укажет направление силы Ампера.
входили в нее, вытянутые пальцы показывали направление тока, тогда отогнутый большой палец укажет направление силы Ампера.
Исходя из формулы (3.22), найдем выражение для силы взаимодействия двух бесконечно длинных, прямых, параллельных друг другу проводников, по которым текут токи I1 и I2 (рис. 3.11) (опыт Ампера). Расстояние между проводами равно a.
Определим силу Ампера dF21, действующую со стороны магнитного поля первого тока I1 на элемент l2dl второго тока.
Величина магнитной индукции этого поля B1 в точке расположения элемента второго проводника с током равна
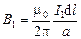 .
.
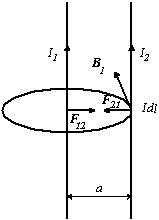
Рис. 3.11 Опыт Ампера по определению силы взаимодействия
двух прямолинейных токов
Тогда с учетом (3.22) получим
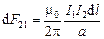 . (3.24)
. (3.24)
Рассуждая точно так же, можно показать, что сила Ампера, действующая со стороны магнитного поля, создаваемого вторым проводником с током, на элемент первого проводника I1dl , равна
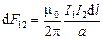 ,
,
т. e. dF12 = dF21. Таким образом, мы вывели формулу (3.1), которая была получена Ампером экспериментальным путем.
На рис. 3.11 показано направление сил Ампера. В случае, когда токи направлены в одну и ту же сторону, то это ‑ силы притяжения, а в случае токов разного направления ‑ силы отталкивания.
Из формулы (3.24), можно получить силу Ампера, действующую на единицу длины проводника
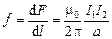 . (3.25)
. (3.25)
Таким образом, сила взаимодействия двух параллельных прямых проводников с токами прямо пропорциональна произведению величин токов и обратно пропорциональна расстоянию между ними.
Закон Ампера утверждает, что на элемент с током, помещенный в магнитное поле, действует сила. Но всякий ток есть перемещение заряженных частиц. Естественно предположить, что силы, действующие на проводник с током в магнитном поле, обусловлены силами, действующими на отдельные движущиеся заряды. Этот вывод подтверждается рядом опытов (например, электронный пучок в магнитном поле отклоняется).
Найдем выражение для силы, действующей на заряд, движущийся в магнитном поле, исходя из закона Ампера. Для этого в формулу, определяющую элементарную силу Ампера
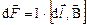 ,
,
подставим выражение для силы электрического тока

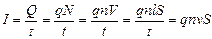 ,
,
где I – сила тока, протекающего через проводник; Q – величина полного заряда протекшего за время t; q – величина заряда одной частицы; N – общее число заряженных частиц, прошедших через проводник объемом V, длиной l и сечением S; n – число частиц в единице объема (концентрация); v – скорость частицы.
В результате получим:
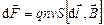 . (3.26)
. (3.26)
Направление вектора  совпадаёт с направлением скорости v, поэтому их можно поменять местами.
совпадаёт с направлением скорости v, поэтому их можно поменять местами.
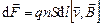 . (3.27)
. (3.27)
Эта сила действует на все движущиеся заряды в проводнике длиной  и сечением S, число таких зарядов:
и сечением S, число таких зарядов:
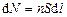 .
.
Следовательно, сила, действующая на один заряд, будет равна:
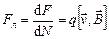 . (3.28)
. (3.28)
Формула (3.28) определяет силу Лоренца, величина которой
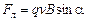 , (3.29)
, (3.29)
где a – угол между векторами скорости частицы и магнитной индукции.
В экспериментальной физике часто встречается ситуация, когда заряженная частица движется одновременно и в магнитном и электрическом поле. В этом случае рассматривают полную силу Лоренца в виде
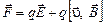 ,
,
где 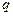 – электрический заряд;
– электрический заряд; 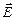 – напряженность электрического поля;
– напряженность электрического поля;  – скорость частицы;
– скорость частицы;  – индукция магнитного поля.
– индукция магнитного поля.
Только в магнитном поле на движущуюся заряженную частицу действует магнитная составляющая силы Лоренца (рис. 3.12)
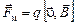 . (3.30)
. (3.30)
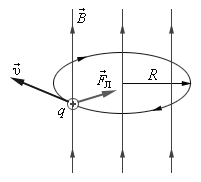
Рис. 3.12 Сила Лоренца
Магнитная составляющая силы Лоренца перпендикулярна вектору скорости и вектору магнитной индукции. Она не изменяет величины скорости, а изменяет только ее направление, следовательно, работы не совершает.
Взаимная ориентация трех векторов ‑ 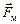 ,
, 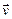 и
и  , входящих в (3.30), показана на рис. 313 для положительно заряженной частицы.
, входящих в (3.30), показана на рис. 313 для положительно заряженной частицы.
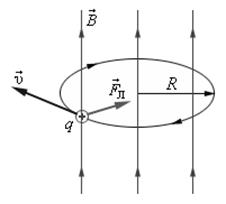
Рис. 3.13 Сила Лоренца, действующая на положительный заряд
Как видно из рис. 3.13, если частица влетает в магнитное поле под углом 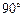 к силовым линиям
к силовым линиям  , то она равномерно движется в магнитном поле по окружности радиусом и периодом обращения:
, то она равномерно движется в магнитном поле по окружности радиусом и периодом обращения:
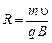 ;
; 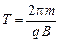 ,
,
где 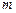 – масса частицы.
– масса частицы.
Отношение магнитного момента 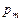 к механическому L (моменту импульса) заряженной частицы, движущейся по круговой орбите,
к механическому L (моменту импульса) заряженной частицы, движущейся по круговой орбите,
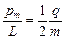 ,
,
где 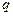 ‑ заряд частицы; т ‑ масса частицы.
‑ заряд частицы; т ‑ масса частицы.
Рассмотрим общий случай движения заряженной частицы в однородном магнитном поле, когда ее скорость направлена под произвольным углом a к вектору магнитной индукции (рис. 3.14). Если заряженная частица влетает в однородное магнитное поле под углом 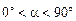 , то она движется по винтовой линии.
, то она движется по винтовой линии.
Разложим вектор скорости на составляющие v|| (параллельную вектору  ) и v^(перпендикулярную вектору
) и v^(перпендикулярную вектору  ):
):
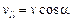
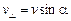 .
.
Наличие v^ приводит к тому, что на частицу будет действовать сила Лоренца и она будет двигаться по окружности радиусом R в плоскости перпендикулярной вектору  :
:
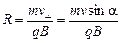 .
.
Период такого движения (время одного витка частицы по окружности) равен
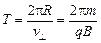 .
.
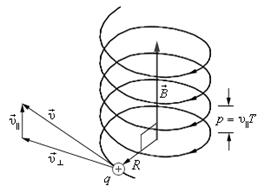
Рис. 3.14 Движение по винтовой линии заряженной частицы
в магнитном поле
За счет наличия v|| частица будет двигаться равномерно вдоль  , так как на v|| магнитное поле не действует.
, так как на v|| магнитное поле не действует.
Таким образом, частица участвует одновременно в двух движениях. Результирующая траектория движения представляет собой винтовую линию, ось которой совпадает с направлением индукции магнитного поля. Расстояние h между соседними витками называется шагом винтовой линии и равно:
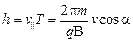 .
.
Действие магнитного поля на движущийся заряд находит большое практическое применение, в частности, в работе электронно-лучевой трубки, где используется явление отклонения заряженных частиц электрическим и магнитным полями, а также в работе масс-спектрографов, позволяющих определить удельный заряд частиц (q/m) и ускорителей заряженных частиц (циклотронов).
Рассмотрим один такой пример, назыаемый «магнитной бутылкой» (рис. 3.15). Пусть неоднородное магнитное поле создано двумя витками с токами, протекающими в одном направлении. Сгущение линий индукции в какой-либо пространнственной области означает большее значение величины магнитной индукции в этой области. Индукция магнитного поля вблизи витков с током больше, чем в пространстве между ними. По этой причине радиус винтовой линии траектории частицы, обратно пропорциональный модулю индукции, меньше вблизи витков, чем в пространстве между ними. После того, как частица, двигаясь вправо по винтовой линии, пройдет среднюю точку, сила Лоренца, действующая на чатицу, приобретает компоненту 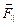 , тормозящую ее движение вправо. В определенный момент эта компонента силы останавливает движение частицы в этом направлении и отталкивает ее влево к витку 1. При приближении заряженной частицы к витку 1 она также тормозится и начинает циркулировать между витками, оказавшись в магнитной ловушке, или между «магнитными зеркалами». Магнитные ловушки используются для удержания в определенной области пространства высокотемпературной плазмы (
, тормозящую ее движение вправо. В определенный момент эта компонента силы останавливает движение частицы в этом направлении и отталкивает ее влево к витку 1. При приближении заряженной частицы к витку 1 она также тормозится и начинает циркулировать между витками, оказавшись в магнитной ловушке, или между «магнитными зеркалами». Магнитные ловушки используются для удержания в определенной области пространства высокотемпературной плазмы ( 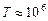 К) при управляемом термоядерном синтезе.
К) при управляемом термоядерном синтезе.
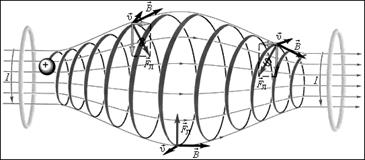
Рис. 3.15 Магнитная «бутылка»
Закономерностями движения заряженных частиц в магнитном поле можно объяснить особенности движения космических лучей вблизи Земли. Космические лучи – это потоки заряженных частиц большой энергии. При приближении к поверхности Земли эти частицы начинают испытывать действие магнитного поля Земли. Те из них, которые направляются к магнитным полюсам, будут двигаться почти вдоль линий земного магнитного поля и навиваться на них. Заряженные частицы, подлетающие к Земле вблизи экватора, направлены почти перпендикулярно к линиям магнитного поля, их траектория будет искривляться. и лишь самые быстрые из них достигнут поверхности Земли (рис. 3.16).
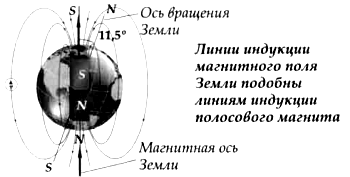
Рис. 3.16 Образование Полярного сияния
Поэтому интенсивность космических лучей доходящих до Земли вблизи экватора, заметно меньше, чем вблизи полюсов. С этим связан тот факт что, Полярное сияние наблюдается главным образом в приполярных областях Земли.
Эффект Холла
В 1880г. американский физик Холл провел следующий опыт: он пропускал постоянный электрический ток I через пластинку из золота и измерял разность потенциалов 
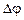 между противолежащими точками A и C на верхней и нижней гранях (рис. 3.17).
между противолежащими точками A и C на верхней и нижней гранях (рис. 3.17).
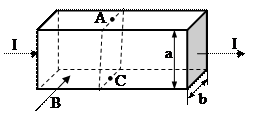
Рис. 3.17 Эффект Холла
В отсутствии магнитного поля 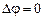 , т. к. для однородной пластины поперечное сечение является эквипотенциальной поверхностью. Когда пластины помещаются в однородное магнитное поле с индукцией
, т. к. для однородной пластины поперечное сечение является эквипотенциальной поверхностью. Когда пластины помещаются в однородное магнитное поле с индукцией  , перпендикулярное к ее боковым граням ‑ между точками A и C возникала разность потенциалов. Это явление было позднее названо эффектом Холла.
, перпендикулярное к ее боковым граням ‑ между точками A и C возникала разность потенциалов. Это явление было позднее названо эффектом Холла.
Экспериментально было обнаружено, что
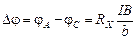 , (3.31)
, (3.31)
где I ‑ сила тока; B ‑ индукция магнитного поля; b ‑ ширина пластины; 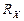 ‑ постоянная Холла.
‑ постоянная Холла.
Дальнейшее исследование показало, что эффект Холла наблюдается во всех проводниках и полупроводниках. Величина константы Холла зависит от материала пластины, причем этот коэффициент для одних веществ положителен, а для других ‑ отрицателен.
Явление Холла можно объяснить, исходя из силы Лоренца. На заряд, движущийся в магнитном поле с индукцией B, действует сила Лоренца
 .
.
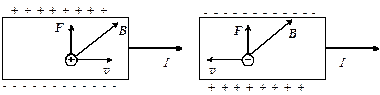
Рис. 3.18 Знак эффекта Холла
Если носителями тока в веществе являются положительные заряды то под действием силы Лоренца эти заряды q отклоняются к верхней грани (при выбранных направлениях  и
и 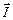 ). Следовательно, вблизи верхней грани возникнет избыток зарядов, а вблизи нижней грани – недостаток зарядов, т. е. возникает разность потенциалов. В случае отрицательных зарядов, как видно из рисунка 3.18, знак разности потенциалов будет противоположым.
). Следовательно, вблизи верхней грани возникнет избыток зарядов, а вблизи нижней грани – недостаток зарядов, т. е. возникает разность потенциалов. В случае отрицательных зарядов, как видно из рисунка 3.18, знак разности потенциалов будет противоположым.
Найдем теперь выражение для 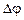 . При возникновении разности потенциалов в пластине возникает электрическое поле в вертикальном направлении. Со стороны этого электрического поля на заряд q будет действовать сила
. При возникновении разности потенциалов в пластине возникает электрическое поле в вертикальном направлении. Со стороны этого электрического поля на заряд q будет действовать сила 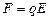 , направленная против силы Лоренца. При некотором значении
, направленная против силы Лоренца. При некотором значении 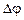 эти силы уравновесят друг друга, и установится равновесный процесс прохождения тока
эти силы уравновесят друг друга, и установится равновесный процесс прохождения тока
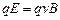 ,
,
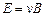 .(3.32)
.(3.32)
Если пластина достаточно длинная и широкая, то поперечное электрическое поле можно считать однородным. Для однородного поля можно написать связь между E и 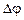 в виде:
в виде:
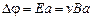 . (3.33)
. (3.33)
Силу тока I можно выразить следующим образом:
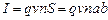 , (3.34)
, (3.34)
где v ‑ скорость упорядоченного движения зарядов; n ‑ число зарядов в единице объема; 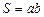 – площадь поперечного сечения пластины.
– площадь поперечного сечения пластины.
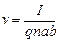 , (3.35)
, (3.35)
подставляя (3.35) в (3.33) получим
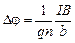 . (3.36)
. (3.36)
Сравнивая эту формулу с экспериментальной (3.31), имеем
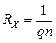 . (3.37)
. (3.37)
Отсюда видно, что, знак константы Холла совпадает со знаком заряда q носителей тока. В полупроводниках носителями тока могут быть электроны ( 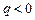 ) и положительные дырки (
) и положительные дырки ( 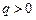 ). На основании измерения константы Холла для полупроводников можно судить о природе его проводимости. При электронной проводимости
). На основании измерения константы Холла для полупроводников можно судить о природе его проводимости. При электронной проводимости 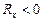 , при дырочной проводимости
, при дырочной проводимости 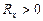 .
.
С помощью константы Холла можно также определить концентрацию носителей тока, если характер проводимости и заряд носителей тока известны (например, для металлов):
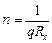 .
.
На принципе, похожем на эффект Холла, основана работа МГД- генераторов (магнитогидродинамических генераторов). В эффекте Холла используется ток проводимости, а можно использовать конвекционный ток. Например, по трубе продувается поток раскаленных газов (следовательно, ионизированных) в магнитном поле. В трубу вводятся электроды, на них возникает разность потенциалов. Величина 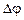 оказывается пропорциональной скорости движения газа. Для увеличения электропроводимости должна быть велика концентрация ионов n, что можно достигнуть повышением температуры газа. Кроме того, в поток газа вводятся специальные присадки ‑ элементы с малой энергией ионизации.
оказывается пропорциональной скорости движения газа. Для увеличения электропроводимости должна быть велика концентрация ионов n, что можно достигнуть повышением температуры газа. Кроме того, в поток газа вводятся специальные присадки ‑ элементы с малой энергией ионизации.
К.П.Д. МГД-генераторов может достигать 50…60%, в то время, как у тепловых электростанций 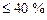 . Также преимуществом МГД-генераторов является то, что в них нет никаких механических движущихся частей и, следовательно, потерь на преодоление трения.
. Также преимуществом МГД-генераторов является то, что в них нет никаких механических движущихся частей и, следовательно, потерь на преодоление трения.
Магнитное поле кругового тока
Рассмотрим магнитное поле постоянного тока /, текущего по проводу в форме окружности С радиуса а. Применим закон Био – Савара – Лапласа для определения магнитной индукции в центре кругового тока.
К расчету магнитного по^хя кругового тока
На рис. 6.2 изображены вектор dl, характеризующий произвольный малый
участок проводника с током, и вектор R , соединяющий этот участок с точкой О, в которой требуется определить магнитную инндукцию В . По определению векторного произведения из формулы (6.1)
следует, что вектор dB магнитной индукции поля, создаваемого рассматриваемым участком тока, перпендикулярен и
вектору dl , и вектору R . Таким образом, начало вектора dB находится в точке О, а сам вектор перпендикулярен плоскости контура С.
Так как векторы dl и R образуют прямой угол, модуль вектора dB согласно формуле (6.3) будет
Векторы dB магнитной индукции полей, создаваемых различными участками контура в точке О, совпадают по направлению. В таком случае их векторная сумма будет представлять собой вектор В , который имеет то же направление. При этом модуль этого вектора будет равен
сумме модулей векторов dB :
Интеграл от dl равен длине окружности:
Таким образом, придем к следующей формуле для магнитной индукции поля, создаваемого круговым током в центре окружности:
Модуль рт вектора магнитного момента кругового тока равен произведению силы тока на площадь круга:
Используя это соотношение, выражение (6.5) можно записать так:
В центре кругового витка с током вектор магнитной индукции направлен так же, как вектор магнитного момента рт. При этом справедливо соотношение
Отметим, что направление вектора магнитной индукции в центре кругового тока связано с направлением электрического тока правилом правого винта.
Линии в пространстве, к которым вектор В в любой точке является касательным, называются силовыми линиями магнитного поля. На рис. б.З изображены силовые линии магнитного поля кругового тока.
Рис. 6.8. Силовые линии магнитного поля кругового тока
Магнитная индукция в центре окружности
Магнитное поле постоянных токов различной конфигурации изучалось экспериментально французскими учеными Ж. Био и Ф. Саваром (1820 г.). Они пришли к выводу, что индукция магнитного поля токов, текущих по проводнику, определяется совместным действием всех отдельных участков проводника. Магнитное поле подчиняется принципу суперпозиции :
Если магнитное поле создается несколькими проводниками с током, то индукция результирующего поля есть векторная сумма индукций полей, создаваемых каждым проводником в отдельности.
Индукцию проводника с током можно представить как векторную сумму элементарных индукций создаваемых отдельными участками проводника. На опыте невозможно выделить отдельный участок проводника с током, так как постоянные токи всегда замкнуты. Можно измерить только суммарную индукцию магнитного поля, создаваемого всеми элементами тока. Закон Био–Савара определяет вклад в магнитную индукцию результирующего магнитного поля, создаваемый малым участком Δ проводника с током .
Здесь – расстояние от данного участка Δ до точки наблюдения, α – угол между направлением на точку наблюдения и направлением тока на данном участке, μ0 – магнитная постоянная. Направление вектора определяется правилом буравчика: оно совпадает с направлением вращения рукоятки буравчика при его поступательном перемещении вдоль тока. Рис. 1.17.1 иллюстрирует закон Био–Савара на примере магнитного поля прямолинейного проводника с током. Если просуммировать (проинтегрировать) вклады в магнитное поле всех отдельных участков прямолинейного проводника с током, то получится формула для магнитной индукции поля прямого тока:
которая уже приводилась в § 1.16.
| Рисунок 1.17.1.
Закон Био–Савара позволяет рассчитывать магнитные поля токов различных конфигураций. Нетрудно, например, выполнить расчет магнитного поля в центре кругового витка с током. Этот расчет приводит к формуле где – радиус кругового проводника. Для определения направления вектора также можно использовать правило буравчика, только теперь его рукоятку нужно вращать в направлении кругового тока, а поступательное перемещение буравчика укажет направление вектора магнитной индукции. Расчеты магнитного поля часто упрощаются при учете симметрии в конфигурации токов, создающих поле. В этом случае можно пользаоваться теоремой о циркуляции вектора магнитной индукции , которая в теории магнитного поля токов играет ту же роль, что и теорема Гаусса в электростатике. Поясним понятие циркуляции вектора Пусть в пространстве, где создано магнитное поле, выбран некоторый условный замкнутый контур (не обязательно плоский) и указано положительное направление его обхода. На каждом отдельном малом участке Δ этого контура можно определить касательную составляющую вектора в данном месте, то есть определить проекцию вектора на направление касательной к данному участку контура (рис. 1.17.2).
|
