Внешний угол треугольника как найти рисунок

Углы треугольника бывают внутренние и внешние. Что такое внешний угол треугольника? Как его найти?

Определение.

Внешний угол треугольника при данной вершине — это угол, смежный с внутренним углом треугольника при этой вершине.

Как построить внешний угол треугольника? Нужно продлить сторону треугольника.

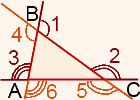
На рисунке:

∠3 — внешний угол при вершине А,

∠2 — внешний угол при вершине С,

∠1 — внешний угол при вершине В.

Сколько внешних углов у треугольника?

При каждой вершине треугольника есть два внешних угла. Чтобы построить внешний угол при вершине треугольника, можно продлить любую из двух сторон, на которых лежит данная вершина. Таким образом получаем 6 внешних углов.

Внешние углы каждой пары при данной вершины равны между собой (как вертикальные):

∠1=∠4,  ∠2=∠5,  ∠3=∠6.

Поэтому, когда говорят о внешнем угле треугольника, не важно, какую из сторон треугольника продлили.

Чему равен внешний угол?

Теорема (о внешнем угле треугольника)

Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

Дано: ∆АВС, ∠1 — внешний угол при вершине С.

Доказать: ∠1=∠А+∠В.

Доказательство:

Так как сумма углов треугольника равна 180º, ∠А+∠В+∠С=180º.

Следовательно, ∠С=180º-(∠А+∠В).

∠1 и ∠С (∠АСВ) — смежные, поэтому их сумма равна 180º, значит, ∠1=180º-∠С=180º-(180º-(∠А+∠В))=180º-180º+(∠А+∠В)=∠А+∠В.

Что и требовалось доказать.

Внешний угол треугольника

• Сумма внешних углов

Внешний угол треугольника — это угол, смежный с любым из внутренних углов треугольника.

При каждой вершине треугольника может быть построено по два равных внешних угла. Например, если продолжить все стороны треугольника  ABC,  то при каждой его вершине получится по два внешних угла, которые равны между собой, как вертикальные углы:

Из данного примера можно сделать вывод, что внешние углы, построенные при одной вершине, будут равны.

Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

Так как внешний угол (∠1) дополняет внутренний угол (∠4) до развёрнутого угла, то их сумма равна  180°:

∠1 + ∠4 = 180°.

Сумма внутренних углов углов любого треугольника тоже равна  180°, значит:

∠2 + ∠3 + ∠4 = 180°.

Из этого следует, что

∠1 + ∠4 = ∠2 + ∠3 + ∠4.

Сократив обе части полученного равенства на одно и тоже число (∠4), получим:

∠1 = ∠2 + ∠3.

Из этого можно сделать вывод, что внешний угол треугольника всегда больше любого внутреннего угла, не смежного с ним.

Сумма внешних углов

Сумма трёх внешних углов треугольника, построенных при разных вершинах, равна  360°

Рассмотрим треугольник  ABC:

Каждая пара углов (внутренний и смежный с ним внешний) в сумме равны  180°.  Все шесть углов (3 внутренних и 3 внешних) вместе равны  540°:

(∠1 + ∠4) + (∠2 + ∠5) + (∠3 + ∠6) = 180° + 180° + 180° = 540°.

Значит чтобы найти сумму внешних углов, надо из общей суммы вычесть сумму внутренних углов:

∠1 + ∠2 + ∠3 = 540° – (∠4 + ∠5 + ∠6) = 540° – 180° = 360°.

Основные определения

Прежде чем рассмотреть определение внешнего угла треугольника, напомним несколько основных определений из начального курса геометрии, а именно:

• угла и треугольника;
• смежных углов;
• параллельных прямых.

Угол и треугольник являются геометрическими фигурами. Угол состоит из точки (вершины) и двух лучей (сторон угла), которые исходят из данной точки. Треугольник представляет собой три точки (вершины), соединённые отрезками (сторонами). Треугольник имеет три угла.

На рисунке ниже смежными углами являются углы $ADB$ и $BDC$. $angle ADB + angle BDC = angle ADC = 180^{circ}$.

Параллельными называются две непересекающиеся прямые на одной плоскости. Секущей по отношению к двум прямым называется прямая, которая пересекает две прямые в двух точках. Если две прямые параллельны, то в случае пересечения пары этих прямых секущей, получившиеся в результате этого действа накрест лежащие углы равны, а сумма односторонних углов равна $180^{circ}$.

Теорема о сумме углов треугольника

Понятие внешнего угла треугольника встречается в теореме о сумме углов треугольника, которая звучит следующим образом:

Приведём её доказательство.

Пусть дан произвольный $triangle ABC$. Нужно доказать, что $angle A + angle B + angle C=180^{circ}$.

Проведём прямую $b$ через вершину $B$, которая будет параллельна стороне $AC$.

Видим, что углы 1 и 5 – накрест лежащие углы при пересечении параллельных прямых $b$ и $AC$ секущей $AB$. Углы 3 и 4 также являются накрест лежащими углами при пересечении тех же параллельных прмяых секущей $BC$. Делаем вывод, что: $angle 5 = angle 1, angle 4 = angle 3$.

Очевидно, глядя на рисунок, что сумма углов 2, 4 и 5 равна $180^{circ}$. Отсюда следует, что $angle 1 +angle 2 +angle 3 = 180^{circ}$ или $angle A + angle B + angle C=180^{circ}$. Ч.т.д.

Внешний угол треугольника

В доказательстве теоремы о сумме углов треугольника есть два примера внешнего угла треугольника. Это углы 4 и 5. Дадим определение:

Имеем теорему:

Докажем эту теорему.

Рассмотрим следующий рисунок:

Мы видим, что угол 4 является внешним углом, смежным с 2 углом треугольника. Очевидно, что $angle 4 +angle 2 = 180^{circ}$. По теореме о сумме углов:

$(angle 1 +angle 3)+angle 2=180^{circ}$. Отсюда следует, $angle 4 = angle 1 +angle 3$. Ч.т.д.

Рассмотрим пример задачи на данную тему.

Таким образом, в данной статье мы получили полное представление о том, что такое внешний угол треугольника и разобрали сопутствующие теоремы.

Внешний угол треугольника

Определение. Внешним углом треугольника называется угол, смежный к любому углу этого треугольника.

На Рис.1 угол 4 внешний так как углы 2 и 4 смежные.

Теорема. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

Доказательство. Докажем, что ( small angle 4=angle 1+ angle 3. ) Поскольку сумма углов треугольника равна 180°, то имеем:

.

(1)

Так как углы 2 и 4 смежные, то:

.

(2)

Вычитая (1) из (2) получим:

,

,

.