Внутренние касательные к двум окружностям как найти

Две окружности на плоскости.
Общие касательные к двум окружностям

Взаимное расположение двух окружностей

Взаимное расположение на плоскости двух окружностей радиусов r₁ и r₂ с центрами O₁ и O₂ определяется расстоянием d между центрами этих окружностей

Расстояние между центрами окружностей больше суммы их радиусов

Расстояние между центрами окружностей равно сумме их радиусов

Расстояние между центрами окружностей равно разности их радиусов

Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов

r₁ – r₂ лежит внутри другой

Расстояние между центрами окружностей меньше разности их радиусов

d r₁ и r₂ с центрами O₁ и O₂ определяется расстоянием d между центрами этих окружностей

Расстояние между центрами окружностей больше суммы их радиусов

Расстояние между центрами окружностей равно сумме их радиусов

Расстояние между центрами окружностей равно разности их радиусов

Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов

r₁ – r₂ лежит внутри другой

Расстояние между центрами окружностей меньше разности их радиусов

d r₁ и r₂ с центрами O₁ и O₂ определяется расстоянием d между центрами этих окружностей

Расстояние между центрами окружностей равно разности их радиусов

Расстояние между центрами окружностей меньше разности их радиусов

d внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.

Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.

Существует единственная общая внешняя касательная. Других общих касательных нет.

Существуют две общих внешних касательных. Других общих касательных нет.

Существует единственная общая внутренняя касательная, а также
две общих внешних касательных. Других общих касательных нет.

Каждая из окружностей лежит вне другой

Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет

Фигура	Рисунок	Свойства
Две окружности на плоскости
Каждая из окружностей лежит вне другой
Внешнее касание двух окружностей
Внутреннее касание двух окружностей
Окружности пересекаются в двух точках
Каждая из окружностей лежит вне другой
Внешнее касание двух окружностей
Внутреннее касание двух окружностей
Окружности пересекаются в двух точках
Каждая из окружностей лежит вне другой
Расстояние между центрами окружностей больше суммы их радиусов
Внешнее касание двух окружностей
Расстояние между центрами окружностей равно сумме их радиусов
Внутреннее касание двух окружностей
Окружности пересекаются в двух точках
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r1 – r2 лежит внутри другой
Внутренняя касательная к двум окружностям
Внутреннее касание двух окружностей
Окружности пересекаются в двух точках
Внешнее касание двух окружностей

Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.

Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.

Существует единственная общая внешняя касательная. Других общих касательных нет.

Существуют две общих внешних касательных. Других общих касательных нет.

Существует единственная общая внутренняя касательная, а также две общих внешних касательных. Других общих касательных нет.

Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет

Внешняя касательная к двум окружностям

Внутренняя касательная к двум окружностям

Внутреннее касание двух окружностей

Окружности пересекаются в двух точках

Внешнее касание двух окружностей

Каждая из окружностей лежит вне другой

Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.

Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.

Существует единственная общая внешняя касательная. Других общих касательных нет.

Существуют две общих внешних касательных. Других общих касательных нет.

Существует единственная общая внутренняя касательная, а также две общих внешних касательных. Других общих касательных нет.

Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет

Формулы для длин общих касательных и общей хорды двух окружностей

Внешняя касательная к двум окружностям

Внутренняя касательная к двум окружностям

Внутреннее касание двух окружностей

Окружности пересекаются в двух точках

Внешнее касание двух окружностей

Каждая из окружностей лежит вне другой

Длина общей внешней касательной к двум окружностям вычисляется по формуле

Длина общей внутренней касательной к двум окружностям вычисляется по формуле

Длина общей хорды двух окружностей вычисляется по формуле

Фигура	Рисунок	Формула
Внешняя касательная к двум окружностям
Внутренняя касательная к двум окружностям
Общая хорда двух пересекающихся окружностей

Длина общей внешней касательной к двум окружностям вычисляется по формуле

Длина общей внутренней касательной к двум окружностям вычисляется по формуле

Длина общей хорды двух окружностей вычисляется по формуле

Внешняя касательная к двум окружностям

Внутренняя касательная к двум окружностям

Общая хорда двух пересекающихся окружностей

Длина общей внешней касательной к двум окружностям вычисляется по формуле

Длина общей внутренней касательной к двум окружностям вычисляется по формуле

Внешняя касательная к двум окружностям

Внутренняя касательная к двум окружностям

Общая хорда двух пересекающихся окружностей

Длина общей хорды двух окружностей вычисляется по формуле Доказательства формул для длин общих касательных и общей хорды двух окружностей Утверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3, Построение общей внутренней касательной к двум окружностям Даны две окружности (а это значит, что даны и их центры O1 и O2). Требуется провести общую внутреннюю касательную к ним, то есть такую касательную, от которой данные окружности лежат по разные стороны. Радиус большей окружности называем R, радиус меньшей окружности — r. Сначала вокруг меньшей окружности построим вспомогательную окружность с тем же центром и с радиусом, равным сумме радиусов двух данных окружностей (R + r). Затем построим из центра большей окружности вспомогательную касательную к вспомогательной окружности. Требуемая внутренняя касательная будет параллельна вспомогательной касательной. Отложим первый вспомогательный луч с началом в точке A. Замерим циркулем радиус большей окружности, и тем же раствором циркуля от начала первого луча отложим отрезок AB, равный R. Теперь циркулем замерим радиус меньшей окружности, и тем же раствором циркуля от точки B отложим отрезок BC, равный r. Получился отрезок AC, равный сумме радиусов двух данных окружностей (R + r). Замерим AC циркулем, и тем же раствором циркуля построим первую вспомогательную окружность с центром в O1. Теперь соединим отрезком центры O1 и O2. Произвольным раствором циркуля строим вторую вспомогательную дугу окружности с центром O1. И тем же раствором циркуля строим третью вспомогательную дугу окружности с центром O2 — так, чтобы третья дуга пересекала вторую в двух точках (называем их D и E). Соединяем D и E отрезком, который пересекает O1O2 в середине — эту точку называем F. Теперь замерим циркулем FO1 и этим раствором циркуля строим четвёртую вспомогательную окружность с центром в F на отрезке O1O2, как на диаметре. Эта четвёртая окружность пересекает первую вспомогательную окружность в двух точках (называем их G и H). Выбираем из этих двух точек ту, которая нам больше нравится (в данном построении это точка H), и соединяем прямой с точкой O2. Прямая HO2 — это касательная к первой вспомогательной окружности, проходящая через центр большой данной окружности. Прямая HO2 пересекла большую окружность в двух точках (называем их K и L). Эти точки равно отстоят от O2 и помогут нам построить перпендикуляр к HO2. Произвольным раствором циркуля проводим пятую вспомогательную дугу окружности с центром в K. Тем же раствором циркуля проводим шестую вспомогательную дугу окружности с центром в L — так, чтоб шестая дуга пересекала пятую в некоторой точке (называем точку M). Соединяем O2 и M прямой — эта прямая (перпендикуляр к HO2) пересекает большую данную окружность в некоторой точке (называем её N). Теперь через N проведём прямую, параллельную вспомогательной касательной HO2. Произвольным раствором циркуля строим седьмую вспомогательную окружность с центром в точке N — так, чтоб седьмая окружность пересекала HO2 в двух точках (точки называем P и Q). Тем же раствором циркуля строим восьмую вспомогательную окружность с центром в Q, и восьмая окружность пересекает вспомогательную касательную HO2 в двух точках (точки называем Z и S). Тем же раствором циркуля проводим девятую вспомогательную дугу окружности с центром в S — так, чтобы девятая дуга пересекала седьмую окружность в некоторой точке (точку называем T). Соединяем N и Т прямой — эта прямая NT и будет требуемой общей внутренней касательной к двум данным окружностям. И вот почему. NT проходит через конец радиуса O2N, лежащий на окружности. Также по построению NT параллельна HO2 и перпендикулярна радиусу O2N — следовательно, NT — касательная к большой данной окружности. Теперь проведём радиус O1H и точку его пересечения с прямой TN называем U. Радиус O1H перпендикулярен касательной O2H — значит, угол O2HU — прямой. Получилось, что в четырёхугольнике UHO2N есть три прямых угла — значит, и четвёртый угол HUN прямой, и UHO2N — прямоугольник, в котором сторона HU равна противоположной стороне O2N, то есть радиусу R. Теперь можем найти длину отрезка O1U (составляющего вместе с UH отрезок O1H). Длина равна разности длин O1H и HU, то есть (r + R) — R = r. Выходит, что U отстоит от O1 на r, то есть U лежит на меньшей данной окружности, а это значит, что TN, проходящая через U — проходит через конец радиуса O1U, лежащий на окружности, и перпендикулярна радиусу, то есть TN — касательная к меньшей данной окружности. Построение закончено. Общие касательные Выясним сколько общих касательных имеют две окружности и как эти общие касательные могут быть расположены. Если две окружности не пересекаются и окружность меньшего радиуса лежит внутри окружности большего радиуса, то они не имеют общих касательных. В другом случае не пересекающиеся окружности имеют четыре общие касательные. внешние общие касательные При этом, если обе окружности лежат по одну сторону от касательной (в одной полуплоскости), то такая касательная называется внешней. внутренние общие касательные Если окружности лежат по разные стороны от общей касательной (в разных полуплоскостях), то такая касательная называется внутренней. Если две окружности имеют внутреннее касание, то у них есть одна общая касательная. При внешнем касании две окружности имеют три общие касательные. Две пересекающиеся окружности имеют две общие касательные. [spoiler title=”источники:”] http://blitztest.ru/geometriya/svojstva-vpisannogo-ugla-kasatelnaya-k-okruzhnosti/postroenie-obshchey-vnutrenney-kasatelnoy-k-dvum Общие касательные [/spoiler]

Касание окружностей

• Внутреннее касание
• Внешнее касание

Говорят, что две окружности касаются, если они имеют единственную общую точку. Эта точка называется точкой касания окружностей. Касание окружностей бывает внутренним и внешним.

Внутреннее касание

Касание называется внутренним, если центры окружностей лежат по одну сторону от точки касания окружностей. Построим две окружности, первая с центром  A  и радиусом  AC,  отметим на радиусе  AC  точку  B,  это будет центр второй окружности с радиусом  BC:

Построенные окружности имеют только одну общую точку  C.  Говорят, что они касаются внутренним образом.

При внутреннем касании двух окружностей, расстояние между их центрами равно разности их радиусов.

Внешнее касание

Касание называется внешним, если центры окружностей лежат по разные стороны от точки касания. Построим две окружности, первая с центром  A  и радиусом  AC,  вторая с центром  B  и радиусом  BC:

Построенные окружности имеют только одну общую точку  C.  Говорят, что они касаются внешним образом.

При внешнем касании двух окружностей, расстояние между их центрами равно сумме их радиусов.

При
вычерчивании контуров предметов
сравнительно часто приходится строить
общие касательные к двум дугам окружностей.
Общая касательная к двум окружностям
может быть внешней, если обе окружности
расположены с одной стороны от нее, и
внутренней, если окружности расположены
с разных сторон касательной.

Построение
общей внешней касательной к двум
окружностям радиусами R и r (рисунок
47). Из центра окружности большего радиуса
– точкиO₁
описывают окружность радиусомR
– r(рисунок
47, а). Находят середину отрезкаO₂O₁
– точкуO₃и из нее проводят вспомогательную
окружность радиусомO₃O₂
илиO₃O_1.Обе проведенные окружности пересекаются
в точкахA иВ. ТочкиO₁
иB соединяют
прямой и в пересечении ее с окружностью
радиусомR
определяют точку касанияD
(рисунок 47, б). Из точкиO₂параллельно прямойO₁D
проводят линию до пересечения с
окружностью радиусомrи получают
вторую точку касанияC.
ПрямаяCDявляется
искомой касательной. Так же строится
вторая общая внешняя касательная к этим
окружностям (прямаяEF).

а
б

Рисунок
47

Построение
общей внутренней касательной к двум
окружностями радиусов R и r (рисунок
48). Из центра любой окружности, например:
точкиO₁,
описывают окружность радиусомR
+r (рисунок
48, а). Разделив отрезокO₂O₁
пополам, получают точкуO₃.
Из точкиO₃как из центра описывают вторую
вспомогательную окружность радиусомO₃O₂
= O₃О₁
и отмечают точки A
и
В
пересечения вспомогательных окружностей.
Соединив прямой точки A
и
O₁
(рисунок
48, б), в пересечении ее с окружностью
радиуса R
получают
точку касания D.
Через центр окружности радиуса r
проводят
прямую, параллельную прямой O₁D,
и
в пересечении ее с заданной окружностью
определяют вторую точку касания С.
Прямая CD
– внутренняя
касательная к заданным окружностям.
Аналогично строится и вторая касательная
EF.

а
б

Рисунок
48

3.3 Сопряжения с помощью дуги окружности

3.3.1 Сопряжение двух прямых дугой окружности

Все
задачи на сопряжение дугой могут быть
сведены к двум видам. Сопряжение
осуществляется либо заданным радиусом
сопрягающей дуги, либо через точку,
заданную на одной из сопрягаемых линий.
В том и другом случаях необходимо
построить центр сопрягающей дуги.

Сопряжение
двух пересекающихся прямых дугой
заданным радиусом R_c
(рисунок 49, а). Так как сопрягающая
дуга должна касаться заданных прямых,
то центр ее должен быть удален от каждой
прямой на величину равную радиусуR_c.
Сопряжение строят так. Проводят две
прямые, параллельные заданным и удаленные
от них на величину радиусаR_cи в пересечении этих прямых отмечают
точкуO – центр
сопрягающей дуги. Из точкиОопускают перпендикуляр на каждую из
заданных прямых. Основания перпендикуляров
– точкиA иB – являются
точками касания сопрягающей дуги. Такое
построение сопряжения справедливо для
двух пересекающихся прямых, составляющих
любой угол. Для сопряжения сторон прямого
угла можно воспользоваться также
способом, указанным на рисунке 49, б.

а
б

Рисунок
49

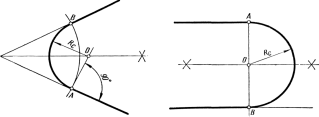
Сопряжение
двух пересекающихся прямых, на одной
из которых задана точка касания А
сопрягающей дуги (рисунок 50).
Известно, что геометрическим местом
центров дуг, сопрягающих две пересекающиеся
прямые, является биссектриса угла,
образованного этими прямыми. Поэтому,
построив биссектрису угла, из точки
касанияA
восстанавливают
перпендикуляр к прямой до пересечения
его с биссектрисой и отмечают точку O
– центр
сопрягающей дуги. Опустив из точки О
перпендикуляр на другую прямую, получают
вторую точку касания В и радиусом R_c=
OA = OB
осуществляют сопряжение двух прямых,
на одной из которых была задана точка
касания.

Сопряжение
двух параллельных прямых дугой, проходящей
через заданную точку касания А (рисунок
51). Из точкиA
восставляют перпендикуляр к заданным
прямым и на пересечении его со второй
прямой отмечают точкуB.
ОтрезокAB делят
пополам и получают точкуО–
центр сопрягающей дуги радиусом.

Рисунок
50 Рисунок 51

Определение

Две окружности, имеющие общую точку, касаются в этой точке, если они имеют в ней общую касательную.

Общая точка двух окружностей называется точкой касания окружностей.

Касание окружностей может быть внешним и внутренним.

Внешнее касание окружностей — это касание, при котором центры окружностей лежат по разные стороны от общей касательной.

Внутреннее касание окружностей — касание, при котором центры окружностей лежат по одну сторону от общей касательной.

Касающиеся окружности имеют только одну общую точку — точку касания.

Утверждение

Центры касающихся окружностей и их общая точка касания лежат на одной прямой.

Доказательство:

При любом виде касания по свойству касательной касательная перпендикулярна радиусам, проведённым в точку касания:

   

По теореме о существовании и единственности прямой, перпендикулярной данной,через точку A можно провести только одну прямую, перпендикулярную данной прямой k.

Следовательно, все три точки: центры окружностей O1, O2 и A лежат на одной прямой.

Что и требовалось доказать.

При внешнем касании расстояние между центрами окружностей равно сумме их радиусов:

   

При внутреннем касании расстояние между центрами окружностей  равно разности радиусов: