Внутренняя реакция как найти ее момент

Привет! В этой статье предлагаю поговорить о реакциях опор, еще известных как опорные реакции. Для успешного освоения курса – «сопротивление материалов», каждый студент должен уметь определять реакции опор, чему учат еще в рамках дисциплины — «теоретическая механика». Но для тех, кто проспал механику на первом курсе, я подготовил данную статью, чтобы каждый желающий мог приобрести навыки по расчету опорных реакций.

Так как этот урок для чайников, я многие моменты буду упрощать и рассказывать только самое основное, чтобы написанное здесь, было понятно даже самому неподготовленному студенту — заочнику.

В рамках статьи рассмотрим 4 примера: двухопорная балка, загруженная посередине пролёта сосредоточенной силой, такая же балка, но загруженная распределённой нагрузкой, консольная балка и плоская рама.

Что такое реакция опоры?

Чтобы лучше понять, что такое реакция опоры (опорная реакция), давай рассмотрим следующий пример — балку (стержень) лежащую на опорах:

На балку давит нагрузка – сила, в свою очередь, балка давит на опоры. И чтобы балка лежала на опорах (никуда не проваливалась), опоры выполняют свою основную функцию — удерживают балку. А чтобы удерживать балку, опоры должны компенсировать тот вес, с которым балка давит на них. Соответственно, действие опор можно представить в виде некоторых сил, так называемых — реакций опор.

Для балки, и нагрузка, и реакции опор, будут являться внешними силами, которые нужно обязательно учитывать при расчёте балки. А чтобы учесть опорные реакции, сначала нужно научиться определять их, чем, собственно, и займёмся на этом уроке.

Виды связей и их реакции

Связи – это способы закрепления элементов конструкций. Опоры, которые я уже показывал ранее – это тоже связи.

 В этой статье будем рассматривать три вида связей: жёсткая заделка, шарнирно-подвижная и шарнирно-неподвижная опора.

Жёсткая заделка

Жёсткая заделка — это один из вариантов закрепления элементов конструкций. Этот тип связи препятствует любым перемещениям, тем самым для плоской задачи, может возникать три реакции: вертикальная (R_A), горизонтальная (H_A) и момент (M_A).

Шарнирно-подвижная и шарнирно-неподвижная опора

В этой статье будем работать с двумя типами опор: шарнирно-подвижной и шарнирно-неподвижной.

В шарнирно-неподвижной опоре возникает две реакции: вертикальная и горизонтальная. Так как опора препятствует перемещению в этих двух направлениях. В шарнирно-подвижной опоре возникает только вертикальная реакция.

Однако, видов связей и их условных обозначений достаточно много, но в рамках этой статьи их все рассматривать не будем. Так как, изученные ранее виды связей, являются основными и практически всегда, при решении задач по сопромату, ты будешь сталкиваться именно с ними.

Что такое момент силы?

Также необходимо разобраться с понятием момент силы.

Момент силы — это произведение силы на плечо. Где плечо — это кратчайшее расстояние от точки до силы, то есть перпендикуляр.

Проиллюстрирую написанное:

Правило знаков для моментов

Также для моментов, нужно задаться каким-то правилом знаков. Я в своих уроках буду придерживаться такого правила:

• если сила относительно точки стремится повернуть ПРОТИВ часовой стрелки, то момент положительный;

• если она стремится повернуть ПО часовой стрелке, то момент отрицательный.

Всю подготовительную информацию дал, теперь будем рассматривать конкретные примеры. И начнём с простейшей расчётной схемы балки.

Определение реакций для двухопорной балки

Возьмём балку, загруженную посередине сосредоточенной силой и опирающейся на шарнирно-неподвижную и шарнирно-подвижную опору:

Введём систему координат: направим ось x вдоль балки, а ось y вертикально. Обозначим реакции в опорах как H_A, R_A и R_B:

Для тех, кто пришёл сюда, ещё будучи на этапе изучения теоретической механики, а я знаю, таких будет много, важно отметить, что в сопромате не принято указывать знаки векторов над силами.

В термехе же, в обязательном порядке, преподаватель от тебя настойчиво будет требовать указывать знак вектора над всеми силами, вот так:

Условия равновесия системы

Чтобы найти все реакции, нужно составить и решить три уравнения — уравнения равновесия:

Данные уравнения являются условиями равновесия системы. А так как мы предполагаем, что опоры обеспечивают это состояние равновесия (удерживают балку). То составив и решив уравнения равновесия — найдём значения опорных реакций.

Первое уравнение называется уравнением проекций — суммой проекций всех сил на координатную ось, которая должна быть равна нулю. Два других уравнения называются уравнениями моментов — суммами моментов всех сил относительно точек, которые должны быть равны нулю.

Уравнения равновесия

Как видишь, чтобы научиться находить реакции опор, главное — научиться правильно составлять уравнения равновесия.

Уравнение проекций

Запишем первое уравнение — уравнение проекций для оси x.

В уравнении будут участвовать только те силы, которые параллельны оси x. Такая сила у нас только одна — H_A. Так как H_A направлена против положительного направления оси x, в уравнение её нужно записать с минусом:

Тогда H_A будет равна:

Поздравляю, первая реакция найдена!

Уравнения моментов

А теперь самое интересное…запишем уравнение моментов, относительно точки A, с учётом ранее рассмотренного правила знаков для моментов.

Так как сила F поворачивает ПО часовой стрелке, записываем её со знаком «МИНУС» и умножаем на плечо.

Так как сила R_B поворачивает ПРОТИВ часовой стрелки, пишем её со знаком «ПЛЮС» и умножаем на плечо. И, наконец, всё это приравниваем к нулю:

Из полученного уравнения выражаем реакцию R_B:

Вторая реакция найдена! Третья реакция находится аналогично, но только теперь уравнение моментов записываем относительно другой точки:

Проверка правильности найденных опорных реакций

Чем хороши задачи на определение реакций, так это тем, что правильность расчёта реакций легко проверить. Для этого достаточно составить дополнительное уравнение равновесия, подставить все численные значения и если сумма проекций сил или сумма моментов будет равна нулю, то и реакции, значит, найдены — верно, а если нет, то ищем ошибку.

Составим дополнительное уравнение проекций для оси y и подставим все численные значения:

Как видишь, реакции опор найдены правильно.

Определение реакций опор для балки с распределенной нагрузкой

Теперь рассмотрим балку, загруженную распределенной нагрузкой:

Перед тем как посчитать реакции опор, распределенную нагрузку нужно «свернуть» до сосредоточенной силы. Если умножить интенсивность q на длину участка, на которой действует нагрузка, получим силу Q. Сила Q будет находиться ровно посередине балки, как и сила F в нашем первом примере:

Подробно комментировать нахождение реакций в опорах здесь, не буду. Просто приведу решение:

Расчёт реакций для консольной балки

Давай рассмотрим теперь пример с жёсткой заделкой – консольную балку. Заодно посмотрим, как учесть силу, приложенную под углом (α = 30^°).

Силу, направленную под определённым углом, нужно разложить на две составляющие – горизонтальную и вертикальную. А их значения найти из силового треугольника:

Покажем реакции в заделке и выполним расчёт:

Для этой задачи выгоднее использовать другую форму условий равновесия:

А выгодна она тем, что из каждого записанного уравнения будем сразу находить реакцию:

Не пугайся отрицательного значения реакции! Это значит, что при указании реакции, мы не угадали с её направлением. Расчёт же показал, что M_A, направлена не по часовой стрелке, а против.

В теоретической механике, когда реакции получают с «минусом» обычно не заморачиваются и не меняют их направление на схеме, так и оставляют в ответе отрицательное значение, оговаривая, что да реакция найдена, но с учётом знака, на самом деле направлена в другую сторону. Потому что найденные реакции в задачах на статику, являются конечной точкой расчёта.

У нас же, в сопромате после нахождения опорных реакций, всё только начинается. Найдя реакции, мы всего лишь находим ВСЕ силы действующие на элемент конструкции, а дальше по сценарию стоит задача определить внутренние усилия, возникающие в этом элементе, расчёты на прочность и т. д. Поэтому на схеме, обязательно следует указывать истинное направление реакций. Чтобы потом, когда будут рассчитываться внутренние усилия ничего не напутать со знаками.

Если получили отрицательное значение, нужно отразить это на схеме:

С учётом изменений на схеме реакция будет равна:

Сделаем проверку, составив уравнение равновесие, ещё не использованное – сумму моментов относительно, скажем, точки B, которая, при правильном расчёте, конечно, должна быть равна нулю:

Если не менять направление реакции, то в проверочном уравнении нужно учесть этот «минус»:

Можешь посмотреть еще один пример, с похожей схемой, для закрепления материала, так сказать.

Реакции опор для плоской рамы

Теперь предлагаю выполнить расчёт плоской рамы. Для примера возьмём расчётную схему, загруженную всевозможными видами нагрузок:

Проводим ряд действий с расчетной схемой рамы:

• заменяем опоры на реакции;
• сворачиваем распределенную нагрузку до сосредоточенной силы;
• вводим систему координат x и y.

Выполняем расчёт реакций опор:

Меняем направление реакции R_A:

В итоге получили следующие реакции в опорах рамы:

Осталось проверить наши расчеты! Для этого предлагаю записать уравнение моментов, относительно точки B. И если, эта сумма будет равна нулю, то расчет выполнен верно:

Как видим, расчет реакций выполнен правильно!

Главный вектор и главный момент сил.

Связи и реакции связей.

Связь осуществляется при помощи гибкого тела, нити, каната или троса. Реакция такой связи приложена к телу в точке прикрепленной к нему нити. Перечислим некоторые типы связей, предполагая, что они изготовлены из абсолютно твердых материалов и трение в местах их соприкосновения с рассматриваемыми телами отсутствует.

2)Шарнирное соединение тел (сферический шарнир, шарнирная опора неподвижная).

Система сходящихся сил.

Системой сходящихся сил наз-ют такую систему сил, линии действия которых пересекаются в одной точке. Сходящиеся системы сил могут быть пространственными или плоскими, расположенные в одной плоскости.

Сходящиеся системы сил могут быть пространственными и плоскими, т.е. расположенными в одной плоскости.

Предположим сначала, что на тело действуют две силы и , приложенные в одной точке A и образующие между собой угол . Равнодействующая этих двух сил, согласно аксиоме о параллелограмме сил, равна сумме этих сил, т.е. (рис.2.1,б)

. Модуль равнодействующей можно определить из треугольника ABC , заметив, что ?ABC=180. по теореме косинусов:

Момент силы относительно точки и оси.

Моментом силы относительно точки называется алгебраическая величина, равная произведению модуля силы на кратчайшее расстояние от точки до линии действия силы.Численное значение момента силы F относительно точки О будем обозначать mo(F). Тогдаmo(F) = ±Fh.Моментом силы относительно оси называется алгебраическая величина момента проекции этой силы на плоскость, перпендикулярную к данной оси, относительно точки пересечения этой плоскости с осью. Момент силы F относительно оси считается положительным, если наблюдатель, смотрящий с положительного направления оси, видит поворот, совершаемый составляющей Fxy силы F, происходящим против хода часовой стрелки.Из определения момента силы относительно оси следует

Момент силы относительно оси равен нулю, если сила параллельна оси или пересекает ее. В обоих случаях сила и ось лежат в одной плоскости. Момент имеет знак +, если сила стремится повернуть тело вокруг центра О против хода часовой стрелки. Знак -, если сила стремится повернуть тело по часовой стрелке. Отметим след. св-во момента сил: момент силы не изм-ся пори переносе точки приложения силы вдоль ее действия. Момент силы относительно центра равен 0 только тогда, когда сила равна 0 или когда линия действия силы проходит через центр О. Момент силы численно равен удвоенной площади треугольника.

9Приведение к равнодействующей силе сходящихся сил.

Сложить 2 силы или неск. сил – это значит найти их равнодействующую. Задача о сложении 2х сил, приложенных к тв. телу в одной точке решается на основании правила параллелограмма.

Системой сходящихся сил называют такую систему сил, линии действия которых пересекаются в одной точке

Сходящиеся системы сил могут быть пространственными и плоскими, т.е. расположенными в одной плоскости.

Предположим сначала, что на тело действуют две силы и , приложенные в одной точке A и образующие между собой угол . Равнодействующая этих двух сил, согласно аксиоме о параллелограмме сил, равна сумме этих сил, т.е.

.величина равнодействующей определится следующей формулой:

Для определения направления равнодействующей к воспользуемся обычными выражениями для направляющих косинусов:

Пара сил и ее момент.

Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на тело. Действие пары сил на тело сводится к вращательному эффекту. Для характеристики этого эффекта вводится понятие момента пары.:Моментом пары называется величина, равная взятому с соответствующим знаком произведению модуля одной из сил пары на ее плечо. Для равновесия пар сил, действующих на твердое тело, необходимо и достаточно, чтобы модуль векторного момента эквивалентной пары сил был равен нулю или чтобы векторный многоугольник, построенный на векторных моментах заданных пар сил, был замкнут.Момент пары считается положительным, если пара стремится повернуть тело против хода часовой стрелки, и отрицательным – если по ходу часовой стрелки.

Главный вектор и главный момент сил.

Главным вектором системы сил называют вектор, равный векторной сумме этих сил.

Главным моментом системы сил относительно точки O тела называют сумму векторных моментов всех сил системы относительно этой точки. Таким образом, основную теорему статики (теорему Пуансо) в краткой форме можно выразить так: Каждую систему сил можно привести к главному вектору и главному моменту относительно произвольного центра.

Система сил на плоскости в теоретической механике

Содержание:

Различные случаи приведения плоской системы сил:

Плоской системой сил называют совокупность сил, расположенных в одной плоскости

Приведение плоской системы сил к точке. Для изучения плоской системы сил, т. е. совокупности сил, приложенных к твердому телу и расположенных в одной плоскости, приведем все силы к центру приведения, выбрав его где-либо в той же плоскости. Тогда мы получим в центре приведения плоский пучок сил, геометрически сложив которые, мы найдем главный вектор системы. Кроме того, при приведении всех сил к точке мы получим пары, расположенные в одной плоскости. Как уже было сказано, в плоской системе моменты сил относительно точки и моменты пар направлены перпендикулярно к плоскости системы в ту или другую сторону. Эти моменты вполне характеризуются величиной и знаком, а потому для вычисления главного момента плоской системы относительно центра приведения, лежащего в плоскости системы, нужно взять алгебраическую сумму моментов всех сил системы относительно центра приведения. Следовательно, система сил, произвольно расположенных на плоскости, эквивалентна главному вектору, равному геометрической сумме всех сил и приложенному к твердому телу в любой точке этой плоскости, и главному моменту, равному алгебраической сумме моментов всех сил относительно той же точки: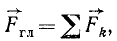

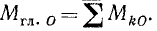
Величину главного вектора удобно вычислить по его проекциям на координатные оси, равным суммам проекций на эти оси всех сил плоской системы:

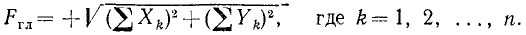(5)

Направление главного вектора можно определить по направляющим косинусам (6′).

Если за центр приведения принято начало координат, то, выражая момент каждой силы плоской системы по (16) и суммируя, получим следующее выражение для главного момента плоской системы сил относительно начала координат:
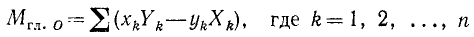(29′)

Задача №1

К твердому телу в точке A (x₁=+10, у =+4) приложена сила F₁ = 3, направленная вниз по вертикали; сила F₂ = 4 направлена по оси Ox в положительную сторону и приложена к тому же телу. Длины выражены в метрах и силы — в ньютонах. Направление осей координат обычное (Ох горизонтально вправо, Oy вертикально вверх). Привести обе силы к началу координат и заменить данную систему сил главным вектором и главным моментом (см. рис. 52).

Решение. Определив сумму проекций данных сил на оси координат, величину главного вектора вычислим по формуле (5), а его направление—по (6′): F_гл=5; cos а=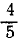=0,800; cosβ = —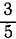=—0,600. Главный момент относительно начала координат вычислим по формуле (29′) или (29): М_{гл. о} = —30.

Ответ. Главный вектор равен 5 н, приложен в начале координат и направлен вправо и вниз под углом 36 о 52′ к оси Ox и 126 о 52′ к оси Оу, главный момент равен —30 н∙м.

Если главный вектор плоской системы сил не равен нулю, то система приводится к одной равнодействующей

Случай приведения к равнодействующей

Величину и направление главного вектора произвольной системы сил определяют по формулам, аналогичным тем, по которым определяют равнодействующую системы сходящихся сил. Между тем главный вектор произвольной системы сил не является равнодействующей этой системы. В самом деле, равнодействующей называют силу, которая одна эквивалентна системе сил, а главный вектор сам по себе не эквивалентен данной системе сил, но эквивалентен ей только в совокупности с главным моментом.

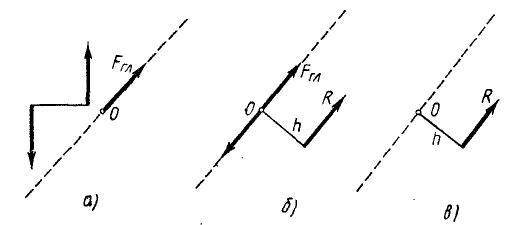
Рис. 51

Главный вектор может быть равнодействующей плоской системы сил лишь в случае, если главный момент системы относительно центра приведения равен нулю. Тогда главный вектор один, без главного момента, эквивалентен данной системе сил.

Следовательно: если главный вектор не равен нулю, а главный момент относительно центра приведения равен нулю, то система приводится к равнодействующей, линия действия которой проходит через центр приведения.

Если же главный момент не равен нулю, то мы можем представить его в виде пары сил, которые мы выберем равными главному вектору, а плечо h—равным отношению величин главного момента и главного вектора (рис. 51,а):

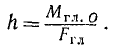(30)

Действие пары на тело не зависит от положения этой пары в ее плоскости, и мы вправе расположить ее так, чтобы одна из сил этой пары была направлена по линии действия главного вектора в сторону, ему противоположную (рис. 51,6). Тогда, отбрасывая эту силу вместе с главным вектором, как взаимно уравновешенные, мы получим только одну силу (рис. 51, в), эквивалентную данной системе; эта сила является равнодействующей данной системы. Мы видим, что равнодействующая по модулю равна главному вектору, параллельна ему по направлению, но отличается от него линией действия.

Следовательно: если главный вектор и главный момент плоской системы сил не равны пулю, то система приводится к равнодействующей, линия действия которой не проходит через центр приведения.

Учитывая, что главный вектор 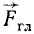по величине и направлению равен равнодействующей 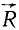(рис. 51), а также учитывая (29), можно равенство (30) переписать так:

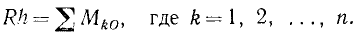(18)

Мы получили теорему Вариньона: момент равнодействующей плоской системы сил относительно какой-либо точки, лежащей в этой плоскости, равен алгебраической сумме моментов составляющих относительно той же точки.

Задача №2

Найти равнодействующую системы сил, заданных в условии задачи №1.

Решение. При решении задачи № 15 данная система приведена к главному вектору 5 н и главному моменту —30 н . м. Представим этот главный момент в виде пары, силы которой по модулю равны главному вектору, а плечо равно отношению величии главного момента и главного вектора, т. е. F= 5 и h=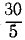=6. Момент пары отрицательный — вращение по стрелке часов. Расположим пару так (рис. 52), чтобы одна из ее сил уравновесила главный вектор. Система приведена к одной силе, равной и параллельной главному вектору, но линия действия этой силы отстоит от начала координат на 6 м. Нетрудно из (29′) получить уравнение линии действия равнодействующей, т. е. —хЗ—у4 — —30.

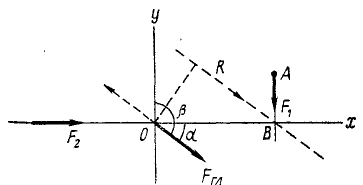
Рис. 52

К тому же результату можно прийти (и в данном случае проще), если заданные силы F1 и Ft перенести в точку В пересечения их линий действия и там сложить.

Ответ. Равнодействующая равна 5 я и лежит на прямой 3x+4y = 30.

Если главный вектор системы сил равен нулю, а главный момент нулю не равен, то система приводится к паре сил

Случай приведения к паре

Исследуем случай, когда главный вектор системы равен нулю, но главный момент системы относительно центра приведения нулю не равен. Если главный вектор системы равен нулю, то, следовательно, нет и равнодействующей. Главный момент мы всегда можем представить в виде пары. Следовательно, если главный вектор равен нулю, а главный момент не равен нулю, то система приводится к паре сил.

Заметим, что главный момент не зависит от центра приведения в том случае, когда главный вектор системы равен нулю. В самом деле, если система сил эквивалентна паре сил с моментом, равным главному моменту системы, а момент пары, как известно (см. § 10), не зависит от центра моментов, то, следовательно, и главный момент (в этом случае) не зависит от центра приведения. Это ясно и из логических соображений: правильно (без ошибок) полученный результат приведения системы сил зависит только от данной системы, но не может зависеть от нашего подсчета. Он существует объективно, независимо от нас. Если система сил эквивалентна паре, то ясно, что, какую бы точку мы ни принимали за центр приведения, мы всякий раз должны получать одну и ту же пару и один и тот же главный момент.

Задача №3

В точках Л, В и C к твердому телу приложены силы 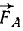, 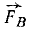и 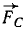. В некотором масштабе (например, 1 н = 1 см) эти силы изображаются направленными отрезками: 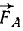=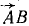, 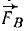=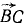, 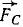= 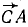(рис. 53, а). Исследовать систему сил.

Решение. Выбрав за центр приведения какую-либо точку, например точку О, и перенеся по методу Пуансо в эту точку все силы, убедимся, что силовой многоугольник замкнут, а следовательно, главный вектор равен нулю. Главный момент системы относительно точки О равен алгебраической сумме моментов трех сил, изображаемых удвоенными площадями треугольников (рис. 53, б):

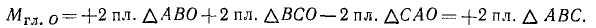
Рис. 53

Независимо от центра приведения О главный момент системы равен удвоенной площади треугольника АВС, т. е. система сил эквивалентна паре.

К такому же результату мы придем путем следующих рассуждений. Главный вектор системы (а следовательно, и равнодействующая) равен нулю, так как силовой многоугольник замкнут. Вместе с тем система данных трех сил не может находиться в равновесии, так как не удовлетворено необходимое условие равновесия трех сил: линии их действия не пересекаются в одной точке. Перенеся силу 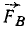(рис. 53, в) по ее линии действия в точку C и сложив ее с силой 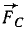, получим равнодействующую этих двух сил, равную и противоположную третьей силе 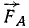и составляющую вместе с ней пару сил.

Ответ. Данная система трех сил эквивалентна паре сил.

Если главный вектор и главный момент системы сил равны нулю, то система сил находится в равновесии

Случай равновесия

Если дана система сил и, приведя ее к какому-либо центру, мы убеждаемся, что и главный вектор и главный момент системы равны нулю, то наличие этой системы эквивалентно ее отсутствию, т. е. система находится в равновесии.

Справедливо и обратное заключение: если данная система сил находится в равновесии, то главный вектор системы и главный момент системы относительно центра приведения равняются нулю. Следовательно, условия
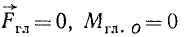(31)

являются необходимыми и достаточными условиями равновесия плоской системы сил. И в этом случае главный момент не зависит от центра приведения. В самом деле, если система сил находится в равновесии, то равновесие не может нарушиться от того, выберем ли мы за центр приведения ту или иную точку плоскости.

Все возможные частные случаи приведения плоской системы сил к данной точке представлены в следующей таблице:

Fгл	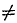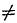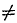0	0	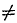0	0
Мгл	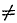0	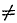=0	0	=0
Равнодействующая не проходит | проходит через центр приведения	Пара сил	Равновесие

Таблица систематизирует возможные случаи приведения плоской системы сил и не нуждается в пояснениях.

Равновесие плоской системы сил

Для равновесия плоской системы сил необходимо и достаточно, чтобы равнялись нулю суммы проекций всех сил на оси координат и сумма моментов всех сил относительно какой-либо точки плоскости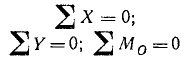

Первая форма уравнений равновесия

Условия равновесия (31) плоской системы сил можно переписать так:
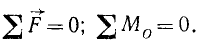(32)

Первое из этих равенств является геометрическим. Мы можем заменить это геометрическое равенство двумя аналитическими, как это было сделано при отыскании аналитической формы условий равновесия плоского пучка сил. Оставляя второе из равенств (32) без изменений, мы получим условия равновесия плоской системы сил в следующем виде:

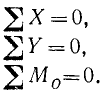(33)

Таким образом, для равновесия системы сил, произвольно расположенных на плоскости, необходимо и достаточно, чтобы равнялись нулю суммы проекций всех сил на оси координат и сумма моментов всех сил относительно какой-либо точки плоскости.

Заметим, что оси координат не обязательно должны быть между собой перпендикулярны, а могут составлять любой отличный от нуля угол, если по условию задачи целесообразно дать им такие направления. Сумму моментов можно взять относительно любой точки плоскости системы сил, поскольку при равновесии системы главный момент ее не зависит от центра приведения.

Соотношения (33) называют условиями равновесия системы сил, произвольно расположенных на плоскости. Если эти соотношения содержат неизвестные величины, то их называют уравнениями равновесия.

Задача №4

Однородная балка AB весом P = 20κΓ опирается на гладкий горизонтальный пол в точке В под углом 60° и, кроме того, поддерживается двумя опорами C и D. Определить реакции опор в точках В, C и D, если длина AB=3м, CB=0,5 м , BD= 1 м (рис. 54).

Решение. Порядок решения задач на равновесие плоской системы сил такой же, как и при решении задач на равновесие плоской системы сходящихся сил, только в данном случае мы имеем три, а не два уравнения равновесия.

Все искомые и известные силы в этой задаче действуют на балку АВ, поэтому рассмотрим равновесие балки АВ.

На балку действуют одна активная сила (собственный вес) и три реакции в трех точках опоры. Реакции, как всегда, направлены перпендикулярно виртуальным перемещениям. Таким перемещением балки АВ, не нарушающим ее связи с полом, является горизонтальное перемещение, и реакцию R_В мы направим вертикально вверх. Давая балке AB мысленные малые перемещения, не нарушающие ее связи с полом, мы не должны беспокоиться о том, чтобы эти перемещения не нарушили связи в других местах, например в точке С. Аналогично, определяя виртуальные перемещения в точке С, мы не заботимся о том, что при этом нарушается связь в точке В. Перемещениями, не нарушающими связи в точках C и D, являются перемещения вдоль балки (подобно смычку по струне), поэтому реакции в точках C и D направим перпендикулярно балке.

Строим оси координат:

Удачный выбор системы координат может упростить уравнения равновесия. Можно пользоваться и косоугольной системой координат, например, направив одну ось горизонтально, а другую—под углом 60° по BA. Мы направим оси, как указано на чертеже. Тогда

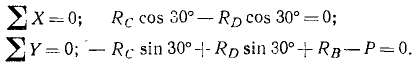
За центр моментов удобнее принимать точку, в которой пересекаются линии действия неизвестных по величине реакций. Так, в данном случае удобно принять точку, в которой пересекаются линии действия реакций R_B и R_C. В результате такого выбора обе эти реакции не войдут в уравнение моментов. Чтобы определить плечо реакции R_D, опустим перпендикуляр из центра моментов на линию действия этой реакции. Нетрудно видеть, что плечо CD = 0,5 м. Чтобы определить плечо силы тяжести, опустим перпендикуляр из центра моментов на линию действия этой силы. Получим 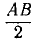cos 60° = 0,75 м. Реакция R_D относительно центра моментов направлена против хода часов (момент положителен), а сила тяжести — по ходу часов (момент отрицателен). Уравнение моментов имеет вид

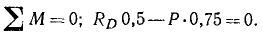
Решая совместно все три уравнения равновесия, получаем ответ.

Для равновесия плоской системы сил необходимо н достаточно, чтобы равнялись нулю суммы моментов всех сил относительно трех каких-либо точек плоскости, не лежащих на одной прямой: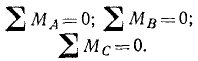

Система сил, действующих на балку АВ, состоит из двух пар сил. Рекомендуем решить эту задачу при помощи уравнения (26′) равновесия системы пар на плоскости, по примеру задачи № 13. Вторая форма уравнений равновесия. Необходимые и достаточные условия равновесия плоской системы сил можно выразить не только равенствами (33). К одному из других видов условий равновесия плоской системы сил приводит теорема, обычно называемая теоремой о трех моментах: для равновесия системы сил, произвольно расположенных на плоскости, необходимо и достаточно, чтобы равнялись нулю суммы моментов всех сил системы относительно каждой из трех точек, произвольно взятых на плоскости, но не лежащих на одной прямой. Докажем эту теорему.

Пусть дана плоская система сил. Возьмем в плоскости произвольную точку А и определим сумму моментов всех сил относительно этой точки. Если бы сумма моментов не равнялась нулю, то система, конечно, не была бы в равновесии. Если же 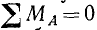, то система может либо находиться в равновесии, либо быть приведенной к равнодействующей, проходящей через точку А (см. таблицу на стр. 79). Следовательно, написанное условие хотя и необходимо, но не достаточно для равновесия системы. Возьмем в той же плоскости другую произвольную точку В и определим сумму моментов всех сил системы относительно точки В. Если 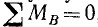, то это равенство вместе с предыдущим все же не может быть достаточным условием равновесия системы, поскольку равнодействующая системы (если она существует) может проходить через обе эти точки, тогда моменты равнодействующей относительно каждой из этих точек, а следовательно, и суммы моментов составляющих (теорема Вариньона) равны нулю, но система не в равновесии, а приводится к равнодействующей, проходящей через точки А и В.

Возьмем сумму моментов всех сил относительно третьей точки, выбрав эту точку C где-либо не на прямой АВ. Если сумма моментов всех сил системы относительно точки C равна нулю, то система находится в равновесии, так как равнодействующая не может проходить через точки А, В и С, не лежащие на одной прямой. Следовательно, три равенства
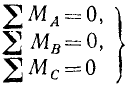(34)

выражают, так же как и равенства (33), необходимые и достаточные условия равновесия системы сил, произвольно расположенных на плоскости.

Если равенства (34) являются уравнениями равновесия, т. е. содержат неизвестные величины, которые нужно определить, то соответствующим выбором центров моментов A, B и C можно составить уравнения так, чтобы каждое из них содержало только одну неизвестную величину, и вместо системы трех уравнений с тремя неизвестными получить три уравнения, каждое из которых содержит только по одной неизвестной.

Задача №5

Однородный стержень длиной 2l и весом P прикреплен в точке В при помощи шарнира к стене (рис. 55), а в точке D опирается на угол другой стены. Найти все реакции, если известно, что точка D отстоит от первой стены на расстоянии а и находится на высоте b над шарниром В.

Решение. Равновесие какого тела надо рассматривать? Ответ на этот вопрос в данной задаче очевиден: равновесие стержня. Какие силы действуют на это тело? На него действуют вес Р, приложенный в середине стержня; реакция R_D в точке D, направленная перпендикулярно виртуальному перемещению, т. е. перпендикулярно стержню; реакция в шарнире В, которую мы раскладываем на две составляющие X_B н Y_B, поскольку направление реакции в шарнире обычно бывает неизвестно, хотя в данном случае это направление можно было бы определить по необходимому условию равновесия трех непараллельных сил . Теперь составляем уравнения равновесия, для чего воспользуемся равенствами (34).

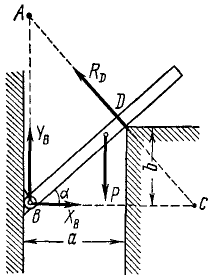
Рис. 55

За центры моментов выберем точки пересечения линий действия искомых сил Эти точки обычно называют точками Риттера. Уравнения равновесия принимают вид:

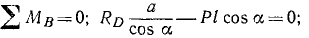
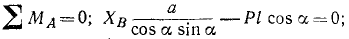
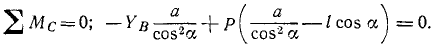
Остается решить эти уравнения, содержащие по одной неизвестной.

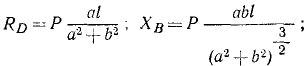
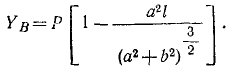
Для равновесия плоской системы сил необходимо и достаточно, чтобы равнялись нулю суммы моментов всех сил относительно двух каких-либо точек плоскости и сумма проекций всех сил на любую ось, не перпендикулярную к прямой, проходящей через эти две точки:

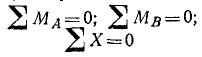
Третья форма уравнений равновесия

Если две из неизвестных сил параллельны друг другу и точка пересечения их, следовательно, уходит в бесконечность, то для решения задачи удобно воспользоваться третьим видом уравнений равновесия. Пусть суммы моментов плоской системы сил относительно произвольно выбранных точек А и В равняются нулю: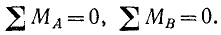

В таком случае, как только что было показано, система сил или находится в равновесии, или приводится к равнодействующей, проходящей через точки А и В. Спроецируем все силы на какую-либо ось, не перпендикулярную к прямой, проходящей через точки А и В. Если система сил . приводится к равнодействующей, лежащей на прямой АВ, то сумма проекций всех сил на g выбранную нами ось должна равняться модулю | этой равнодействующей, помноженному на коси- | нус утла между осью и прямой АВ. Если же система находится в равновесии, то сумма проекций всех сил равняется нулю. Обратно, если сумма | проекций всех сил на эту ось равна нулю, то, следовательно, равна нулю равнодействующая, т. е. эта система находится в равновесии.

Таким образом, для равновесия системы сил, расположенных на плоскости, необходимо и достаточно, чтобы равнялись нулю суммы моментов всех сил системы относительно двух произвольно
выбранных точек плоскости и сумма проекций всех сил системы на какую-либо ось Ох, не перпендикулярную к прямой, проходящей через выбранные центры моментов:
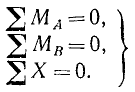(35)

Задача №6

Между двумя вертикальными стенами, находящимися на расстоянии а друг от друга (рис. 56), помещен стержень весом P и длиной 21, который может вращаться вокруг шарнира А. прикрепляющего конец его к одной из стен. Найти реакции опор.

Решение. 1. Равновесие какого тела надо рассмотреть? Равновесие стержня.
2. Какие силы на это тело действуют? Вес Р; реакция в точке D, направленная перпендикулярно виртуальному перемещению стержня (стержень, не нарушая связи, можно перемещать вдоль стены, поэтому реакция Rq направлена перпендикулярно стене DC); реакция в шарнире А, которую мы разложим на X_А и Y_А.
3. Составим уравнения равновесия в третьей форме, выбрав за центры моментов точки А и В, в которых пересекаются линии действия искомых реакций. Точка пересечения Rq и Xa находится в бесконечности, поэтому в качестве третьего уравнения возьмем сумму проекций всех сил на какую-либо ось, лишь бы эта ось не была перпендикулярна к АВ. Имеем

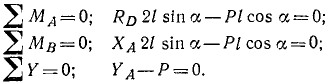
Определив из чертежа sin а и cos а и решая эти уравнения, содержащие по одной неизвестной, найдем ответ.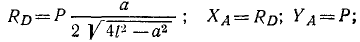

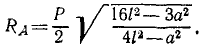
Для равновесия плоской системы параллельных сил необходимо и достаточно, чтобы равнялись нулю суммы проекций всех сил на какую-либо ось, не перпендикулярную линиям действия сил, и сумма моментов относительно какой-либо точки: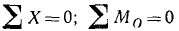

Условия равновесия плоской системы параллельных сил

Если все силы системы параллельны друг другу, то одно из трех уравнений становится следствием двух Других.

В самом деле, в этом случае линия действия главного вектора (если он не равен нулю) параллельна линиям действия всех сил и для его определения достаточно взять сумму проекций всех сил на ось, параллельную их лилиям действия. Если сумма проекций всех сил равна нулю, то и главный вектор равен нулю. Если же, кроме того, равен нулю и главный момент, то система находится в равновесии. Справедливо и обратное заключение: если система параллельных сил, расположенных на плоскости, находится в равновесии, то равняются нулю сумма проекций сил на любую ось и сумма моментов сил относительной любой точки плоскости:

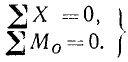(36)

Ось Ox может быть и не параллельной линиям действия сил, а составлять с ними какой-либо угол, кроме прямого.

Для равновесия плоской системы параллельных сил необходимо и достаточно, чтобы равнялись нулю суммы моментов всех сил относительно двух точек плоскости, не лежащих на прямой, параллельной линиям действия сил: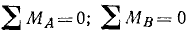

Пусть дана система сил, расположенных в одной плоскости и параллельных друг другу. Возьмем на этой плоскости произвольную точку А. Если 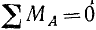, то система может либо находиться в равновесии, либо быть приведенной к равнодействующей, проходящей через точку А параллельно линиям действия составляющих сил. Возьмем сумму моментов всех сил относительно какой-либо точки В, выбрав эту точку так, чтобы прямая AB не была параллельна силам системы. Если сумма моментов относительно этой точки равна нулю, то система находится в равновесии, потому что равнодействующая не может проходить через точки А и В, так как должна быть параллельной силам системы. Поэтому равенства

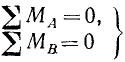(37)

являются необходимыми и достаточными условиями равновесия плоской системы параллельных сил.

Задача №7

На двухконсольную горизонтальную балку действует пара сил (PP), на левую консоль —равномерно распределенная нагрузка интенсивности р, а в точке D правой консоли — вертикальная нагрузка Q. Определить реакции опор, если P=1Т, Q=2Т, p=2T∕м, а =0,8 м (рис. 57).

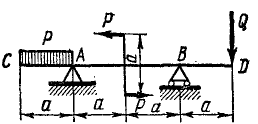
Рис. 57

Решение. Иногда (как в данной задаче), кроме сил, действующих на тело, имеется пара, заданная моментом. Силы пары равны и противоположны, поэтому пара сил не входит в уравнения проекций, но входит в уравнения моментов.

Рассмотрим равновесие балки CD. На балку действуют: 1) пара сил (PP) с моментом +P∙a= 0,8 T∙m∙, 2) вертикальная сосредоточенная нагрузка Q = 2T, приложенная в точке О; 3) равномерно распределенная нагрузка, которую заменяем одной вертикальной силой (равнодействующей) p∙α=1,6T, приложенной в середине CA; 4) реакция R_В в подвижной опоре В, направленная перпендикулярно виртуальным перемещениям, т. е. вертикально; 5) реакция R_А в неподвижном шарнире А. Направление реакции в неподвижном шарнире, вообще говоря, неизвестно. Если повернем пару, изображенную на чертеже, на 90°, отчего, как известно, действие пары на балку не изменится, то все силы, действующие на балку, станут вертикальными, следовательно, и реакция R_А вертикальна. Для решения задачи составим уравнение равновесия в форме (36):

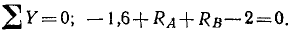
Пара сил в это уравнение не входит, но обязательно должна войти в уравнение моментов: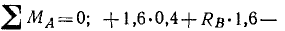

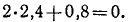
Решая совместно два этих уравнения, получим ответ.
Можно воспользоваться также и уравнениями (37). Тогда вместо уравнения проекций надо составить второе уравнение моментов: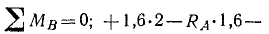

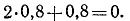
Решая первое уравнение, найдем R_В, решая второе, найдем R_А.
Ответ. R_А=1,5Т, R_В = 2,1Т.

Задача №8

Балка AB длиной 4 м, весом 200 кГ может вращаться вокруг горизонтальной оси А и опирается концом В на другую балку CD длиной 3 м, весом 160 кГ, которая подперта в точκe E и соединена со стеной шарниром D. В точках M и N помещены грузы по 80кГ каждый. Расстояния: AM=3м, ED = 2м, ND=1м. Определить опорные реакции (рис. 58, а).

Решение. Балки AB и CD не являются одним твердым телом, а представляют собой систему сочлененных тел. Рассмотрим отдельно равновесие каждого тела под действием всех приложенных к этому телу сил.

1-й вопрос: равновесие какого тела рассматривать?
Ответ: равновесие балки АВ.

2-й вопрос: какие силы действуют на это тело?
Ответ: на балку AB действуют (рис. 58, б):

Рис. 58

а) собственный вес балки 200 кГ, приложенный к середине балки н направленный по вертикали вниз;
б) вес 80кГ груза М, направленный по вертикали вниз;
в) реакция R_В со стороны балки CD, поддерживающей балку АВ. Эта реакция приложена к балке AB в точке В и направлена по вертикали вверх;
г) реакция R_А в шарнире А. Эта реакция вертикальна, так как балка находится в равновесии, а все остальные действующие на балку силы направлены по вертикали. Нетрудно сообразить, что R_А направлена вверх.
Уравнения равновесия можно составить в форме (36) или в форме (37) по нашему желанию. Составим их в форме (37), приравняв нулю суммы моментов относительно точки А и относительно точки В:

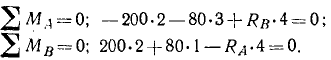
Решая эти уравнения, находим R_А= 120 кГ, R_В = 160 кГ.

Теперь приступаем ко второй части задачи и опять задаем себе тот же вопрос: равновесие какого тела рассматривать? На этот раз рассмотрим равновесие балки CD. Какие силы на нее действуют? На нее действуют (рис. 58, в):
а) собственный вес балки 160 кГ, приложенный в середине балки;
б) вес 80 кГ груза N, приложенный между опорами E и D;
в) давление балки АВ, приложенное к балке CD в точке С, направленное по вертикали вниз и (по закону равенства действия и противодействия) равное реакции R_В, а следовательно, равное 160 кГ;
г) реакция R_Е, прило/кенная в точке E и направленная вверх;
д) реакция RD. Эта реакция должна быть вертикальной, так как вертикальны все остальные действующие на балку силы, а балка находится в равновесии. Однако трудно сказать (без предварительных вычислений), направлена ли эта реакция вверх или вниз. При составлении уравнений равновесия примем условно, что RD направлена вверх, но если в результате решения уравнений мы получим отрицательную величину реакции RD, то это будет означать, что мы реакцию направили неверно, и тогда изменим ее направление на обратное. При правильном направлении сил значения их из уравнений равновесия должны всегда получаться положительными.

Возьмем сумму проекций всех сил на вертикальную ось и сумму моментов всех сил относительно точки D:

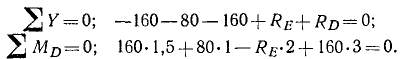
Решая эти уравнения, находим ответ.
Ответ. R_А= 120 кГ, R_В =160 кГ, R_Е= 400 кГ, RD = 0.

Статически определенной задачей называют задачу о равновесии, в которой число неизвестных равно числу уравнений равновесия

Итак, имеется только два уравнения равновесия системы параллельных сил, расположенных в одной плоскости, вместо трех уравнений равновесия системы сил, расположенных на плоскости произвольно. Равновесие плоского пучка сил определяется двумя уравнениями, если же силы пучка не лежат в одной плоскости, то появляется третье уравнение равновесия, как это показано в гл. III.

В системе уравнений число неизвестных не должно превышать числа уравнений, иначе система уравнений не имеет однозначных решений.

Статически определенными задачами называют задачи о равновесии твердого тела, в которых число неизвестных равно числу уравнений равновесия. В противном случае задачи не могут быть решены методами статики и являются статически неопределенными.

Равновесием системы тел называют такое состояние, при котором каждое из тел находится в равновесии

Равновесие системы сил. Часто встречается необходимость в статическом расчете системы тел, так или иначе соединенных («сочлененных») между собой.

Силы, действующие на тела такой системы, можно подразделить на две категории: внешние – силы, приложенные к телам данной системы, но обусловленные наличием других тел, не входящих в эту систему, и внутренние – силы взаимодействия между телами одной и той же системы. Такое подразделение относится как к активным силам, так и к реакциям связей.

Если система находится в равновесии, то в равновесии находится каждое тело, входящее в состав этой системы. Мы можем рассматривать каждое тело отдельно от других тел системы и составить уравнения равновесия всех сил, приложенных к этому телу, не исключая и сил, обусловленных действием на это тело соседних тел системы, т. е. внутренних сил системы, приложенных к этому телу. Так было сделано, например, при решении задачи № 22 о равновесии двух балок.

Вместе с тем, пользуясь аксиомой затвердения, мы можем всю систему рассматривать как одно абсолютно твердое тело и составить уравнения равновесия всех внешних сил системы. Внутренние же силы в эти уравнения равновесия всей системы не входят, так как они взаимно уравновешиваются по принципу равенства действия и противодействия, поскольку взаимодействия каждых двух тел «затвердевшей» системы оказываются приложенными к частям одного абсолютно твердого тела.

Задача №9

На невесомую трехшарнирную арку ABC (рис. 59, а)

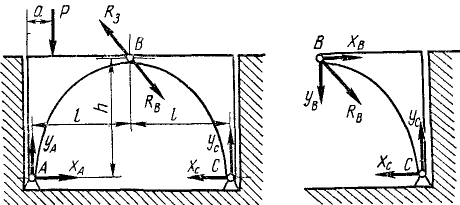
Рис. 59

действует вертикальная сила Р. Определить реакции шарниров А, В и С. Размеры указаны на чертеже.

Решение. Конструкция состоит из двух полуарок AB и ВС, сочлененных шарниром В. Собственным весом полуарок пренебрегаем, поэтому на арку ABC действуют следующие внешние силы: вертикальная сила P и реакции в шарнирах А и С.

Между полуарками имеется взаимодействие в точке В их сочленения. Одна нз этих внутренних сил системы приложена к полуарке АВ, другая равна ей по величине, обратна по направлению, но приложена к полуарке ВС. Если всю арку рассматривать как твердое тело, то эти две силы учитывать не надо, так как они оказываются приложенными к одному твердому телу и, следовательно, взаимно уравновешивают друг друга. В уравнения равновесия всей арки войдут только внешние силы системы: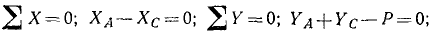

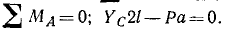
Имеем три уравнения с четырьмя неизвестными.
Для определения горизонтальной реакции в шарнире С, а также R_В, рассмотрим равновесие всех сил, действующих на полуарку ВС. На эту полуарку действуют (рис. 59, б): реакции X_С и Y_С в шарнире C (внешние реакции системы) и реакция в шарнире В (внутренняя реакция для всей системы, но внешняя для полуарки ВС) со стороны полуарки АВ. Эту реакцию мы тоже разложим по осям координат на X_В и Y_В- Составим уравнения равновесия для полуарки ВС: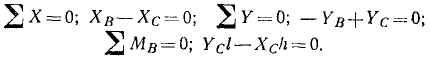

Мы получили три уравнения, содержащие четыре неизвестных, но две из этих неизвестных входят также и в предыдущие три уравнения. Всего мы имеем шесть уравнений с шестью неизвестными. Решая уравнения, получим ответ.

Ответ.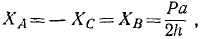

Жесткая заделка

Задачи на тему: жёсткая заделка

Задача №10

Брус, вес которого Р= 100 кГ, приложен в точке С, жестко заделан в стену, образуя с ней угол а =60° (рис. 60, а). Внутри угла DAВ лежит цилиндр весом Q = 180 кГ, касающийся бруса в точке Е, причем АЕ=0,3 м и AC = 0,4 м. Определить реакцию заделки.

Решение. Если балка заделана в стену, то на заделанный конец балки действует система распределенных сил (реакций). Приведем их по методу Пуансо к точке А, заменим одной неизвестной реакцией заделки (с проекциями X_А и Y_А) и одним неизвестным моментом заделки М. Эти три неизвестные определим из уравнений равновесия сил, действующих па балку.

Чтобы определить реакцию заделки (X_А, Y_А и М), надо составить три уравнения равновесия сил, действующих на брус, и, решив их, найти три неизвестные величины. Однако среди сил, действующих на брус, имеется еще одна неизвестная (четвертая)—сила давления F цилиндра, приложенная к брусу в точке Е.

Для определения этой силы предварительно рассмотрим равновесие цилиндра (рис. 60, б), на который действуют вес Q = 180 кГ, реакция R’ стены, направленная горизонтально вправо (перпендикулярно виртуальным перемещениям цилиндра вдоль стены), и реакция R” бруса, направленная влево вверх, перпендикулярно брусу (перпендикулярно виртуальным перемещениям цилиндра по брусу). По принципу равенства действия и противодействия эта реакция R” по величине равна, а по направлению противоположна силе F давления цилиндра на брус.

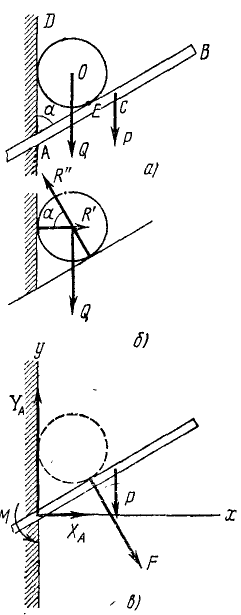
Рис. 60

Из системы сил, действующих на цилиндр, надо определить лишь одну (R” ), а потому достаточно одного уравнения равновесия, если составить его так, чтобы в него не входила другая неизвестная (R”)> Таким уравнением может быть уравнение 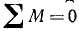относительно какой-либо точки, лежащей на линии действия R’ (кроме точки 0), или 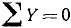. Сумма проекций на вертикальную ось всех сил, приложенных к цилиндру, имеет вид

откуда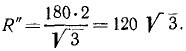

Сила F давления цилиндра на брусок равна 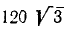, но направлена в противоположную сторону (рис. 60, в).

Кроме силы F, на брусок действуют его вес Р = 100 кГ и реакция в заделке, которую мы представили проекциями X_А и Y_А, а также моментом М.

Уравнения проекций и моментов всех сил, приложенных к бруску, напишем, приняв за центр моментов точку А:

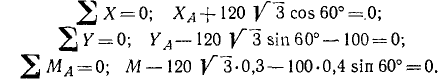
Решая эти уравнения, находим неизвестные величины.

Ответ. X_А =—103,8 кГ; Y_А = +280 кГ . M = +96,9 кГ . м.

Знак минус перед реакцией X_A показывает, что направление реакции противоположно принятому на рис. 60, в. Это и очевидно, так как давление цилиндра стремится выдернуть брусок из заделки.

Определение внутренних усилий в стержнях фермы

Задачи на тему: Определение внутренних усилий в стержнях фермы

Задача №11

Определить опорные реакции и усилия в стержнях фермы крана (рис. 61, а) при нагрузке G = 8 Т. Весом стержней пренебречь.

Решение. В задаче требуется определить опорные реакции и внутренние усилия в стержнях фермы. Под фермой понимают жесткое сооружение, состоящее из стержней, соединенных шарнирами.

Для определения опорных реакций рассмотрим равновесие крана. На кран действуют три внешние силы: 1) вес груза G = 8T; 2) реакция R₂ в опоре O₂, направленная вертикально вверх, перпендикулярно виртуальным перемещениям, и 3) реакция R₁ в шарнире O₁. Реакции в шарнирах мы обычно раскладывали по координатным осям и определяли проекции из уравнений равновесия. Очевидно, что в данном случае проекция R₁ на горизонтальную ось равна нулю, потому что все остальные действующие на кран внешние силы вертикальны, следовательно, вертикальна и реакция R₁. Эта реакция направлена вниз, так как груз стремится повернуть кран вокруг опоры O₂.

Определим плечо силы G относительно O₂. Треугольник O₁AO₂ равносторонний и AO₂ = 3 л. В прямоугольном треугольнике ABO2 катет AO2 равен половине гипотенузы, следовательно, угол AO₂В = 60°. Таков же угол, составляемый BO₂ с горизонтальной прямой, и искомое расстояние h = 6 cos 60° = 3. Итак,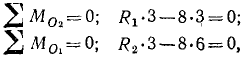

откуда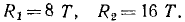

Переходим к определению внутренних усилий в стержнях фермы. Как уже было сказано (см. задачу № 8), усилием в стержне называют силу, действующую вдоль стержня, растягивающую или сжимающую его; если стержень растянут, то на шарнир действует сила, направленная к стержню, а если сжат, то от него. В уравнения равновесия, выводимые в статике твердого тела, входят только внешние силы, потому что внутренние силы согласно принципу равенства действия и противодействия попарно равны и противоположны.

Для определения внутренних усилий в стержнях фермы надо рассмотреть равновесие не всей фермы, а лишь части ее, мысленно разрезав ферму, отбросив одну из отрезанных частей и заменив отброшенную часть силами, направленными вдоль разрезанных стержней. Этот метод определения внутренних усилий 1 называют методом РОЗ по первым буквам слов, определяющих те операции, которые надо проделать (разрежем, отбросим, заменим).

Итак, для определения внутренних усилий в стержнях фермы надо сначала определить реакции, а потом:
1) разрежем мысленно ферму на две части, но так, чтобы разрезано было не более трех стержней с неизвестными усилиями, потому что мы имеем всего три уравнения равновесия. При этом нельзя разрезать ферму так, чтобы все три разрезанных стержня с неизвестными усилиями были между собой параллельны или же все три сходились в одной точке, потому что для этих случаев мы имеем всего по два уравнения. Например, если усилия в стержнях AO₁, AO₂ и AB неизвестны, то не следует мысленно отрезать узел А. Можно сначала отрезать узел В, определить усилие в стержне АВ, а затем уж отрезать узел А, тогда из двух уравнений равновесия сил, приложенных к шарниру А, определим усилия в стержнях AO₁ и AO₂. C этим ограничением можно не только разрезать ферму, но и вырезать из фермы отдельные шарниры. Разрежем ферму крана, как показано на чертеже (рис. 61, б);

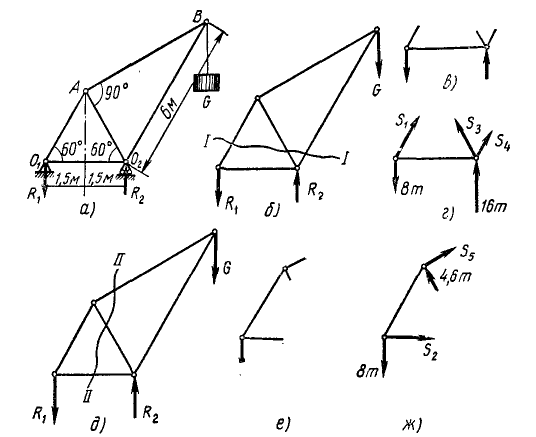
Рис. 61

2) отбросим мысленно одну из частей, на которые разрезана ферма. Принципиально говоря, безразлично, которую из частей отбросить. Отбросим верхнюю часть (рис. 61, в). В результате этих действий жесткость фермы нарушилась бы и, чтобы сохранить равновесие оставленной части фермы, необходимо к ней приложить внешние силы, в точности такие же, как внутренние усилия в соответствующих стержнях неразрезанной фермы. Поэтому мы
3) заменим отброшенную часть фермы неизвестными по величине силами, направив их по разрезанным стержням в сторону от оставленной части, т. е. наружу (рис. 61, г). Если среди разрезанных стержней имеются такие стержни, усилия в которых известны, то наружу мы их направляем только в том случае, если стержень растянут; когда стержень сжат, мы направляем вектор, изображающий это усилие внутрь, к шарниру. Эти силы, равные внутренним усилиям в стержнях, обозначают буквой S с индексом, соответствующим номеру стержня. Теперь составим уравнения равновесия оставленной части фермы. Здесь удобно применить третий вид (35) уравнений равновесия: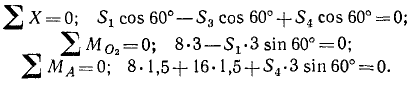

Решая эти уравнения, находим

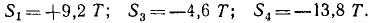
Знаки минус при полученных из уравнений значениях усилий в третьем и в четвертом стержнях показывают, что направления сил на рис. 60, г нужно изменить на противоположные, так как эти стержни не растянуты, а сжаты.
Чтобы определить усилия в других стержнях, надо снова применить метод РОЗ, разрезав ферму по другим стержням;
4) разрежем ферму, как показано на чертеже (рис. 60,д);
5) отбросим одну часть, например правую (рис. 60, е);
6) заменим отброшенную часть силами, направленными по стержням.
Если усилие в стержне неизвестно, то условно считаем, что стержень растянут, и направляем силу от шарнира: S₅ и S₂ (рис. 60, ж). Если же усилие в разрезанном стержне уже известно, то направляем его от шарнира, когда стержень растянут, и к шарниру, когда стержень сжат (усилие в третьем стержне, равное 4,6 T на рис. 60, ж). Затем составляем и решаем уравнения равновесия:

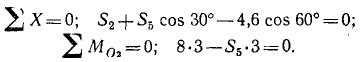
Из этих двух уравнений находим S₂ и S₅.

Заметим, что ферму (и вообще всякую неизменяемую механическую систему) называют статически определимой, если внутренние усилия ее элементов при любой нагрузке могут быть найдены из уравнений статики. В противном случае систему называют статически неопределимой.

Силы трения

Максимальное значение силы трения скольжения равно произведению нормального давления и коэффициента трения: F_мaκc = fN

Кулоново трение

Трение материальных тел связано с явлениями не только механического, но и электрического, термического, внутримолекулярного и пр. характера, и изучение трения относится к области физики. Трудами советских и зарубежных ученых открыты законы и выведены формулы, определяющие силы трения. Точные формулы очень сложны, но в технике обычно пользуются для приближенного определения трения простыми соотношениями, установленными еще в XVIII в. Ш. Кулоном опытным путем. Для вывода закона трения по Кулону проделаем опыт, обычно называемый опытом Морена, по имени одного из основателей научной практической механики. Однако этот же опыт еще задолго до Морена проделал Amohtoh — один из первых серьезных исследователей трения.

К телу (рис. 62), лежащему на горизонтальной негладкой плоскости, прикреплена перекинутая через блок нить, к другому концу которой привязана чашка с грузом. На тело действуют следующие силы: вес G, реакция R плоскости, натяжение Q нити, равное весу груза, приложенного к концу нити, сила трения F_тр направленная против натяжения нити. Из условия равновесия тела следует, что при покое тела сила трения равна и противоположна той силе Q, которая стремится вывести это тело из состояния покоя.

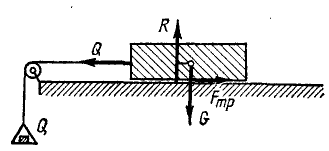
Рис. 62

Постепенно увеличивая груз Q, а следовательно, и натяжение нити, мы убедимся, что тело начнет двигаться, как только это натяжение достигнет определеной величины. До тех пор, пока натяжение нити меньше этой величины, оно уравновешивается силой трения, и тело находится в покое. Отсюда можно сделать заключение: при покое тела увеличение силы, стремящейся привести тело в движение, вызывает увеличение силы трения от нуля до известного предела F_мaκc, больше которого сила трения быть не может. Этот предел называют силой трения скольжения при начале движения:

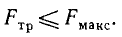(38)

Как показывает опыт, максимальное значение силы трения пропорционально нормальному давлению:

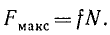(39)

Под нормальным давлением мы понимаем составляющую полного давления, перпендикулярную к соприкасающимся плоскостям. Так, если тело веса G лежит на плоскости, составляющей угол а с плоскостью горизонта (см. рис. 63). то нормальное давление N = Gcos а.

Безразмерный коэффициент пропорциональности

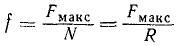
называют статическим коэффициентом трения скольжения.
Сопоставляя равенства (38) и (39), находим, что во время покоя тела действующая на тело сила трения

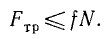(38 / )

После начала движения коэффициент трения скольжения несколько уменьшается и принимает значение динамического коэффициента трения скольжения:

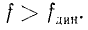
Согласно приближенным кулоновым законам трения коэффициенты трения скольжения не зависят ни от давления, ни от величины трущихся поверхностей, ни от скорости. Они зависят от физической природы трущихся тел, от шлифовки поверхностей, от расположения волокон и, конечно, от смазки. Числовые значения статического и динамического коэффициента трения имеются в любом техническом справочнике.

Статический коэффициент трения скольжения равен тангенсу угла трения.

Угол трения, тангенс трения, конус трения

Коэффициенты трения легко можно определить экспериментальным путем. Пусть тело (рис. 63) лежит на наклонной плоскости OA, угол наклона которой мы можем изменять по нашему желанию. На тело действуют три силы: вес G, сила трения скольжения F_тр, направленная вдоль плоскости соприкосновения тел, и реакция R плоскости, перпендикулярная к этой плоскости, по величине равная нормальному давлению N.

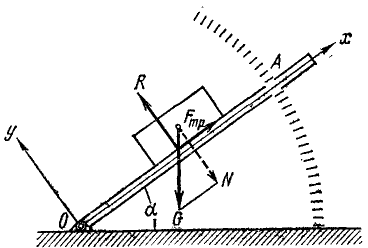
Рис. 63

Будем постепенно увеличивать угол наклона до тех пор, пока тело не начнет двигаться вниз по плоскости. Угол наклона плоскости, при котором начинается скольжение, называют углом трения α_тр для данной пары трущихся материалов. Если, например, тело сделано из бронзы, а плоскость стальная, то α_тр есть угол трения бронзы по стали.

Построим оси координат, как показана на чертеже, и составим уравнения равновесия:

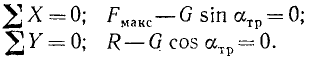
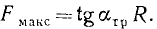
Сравнивая это равенство с (39), находим, что статический коэффициент трения скольжения равен тангенсу угла трения. Тангенс угла трения иногда коротко называют тангенсом трения.

Реакцию, перпендикулярную к опорной поверхности (рис. 64, а), называют идеальной реакцией в отличие от полной реакции, выражающейся геометрической суммой идеальной реакции и силы трения.

Таким образом, сила трения является касательной составляющей полной реакции, идеальная реакция — нормальной составляющей полной реакции, а угол трения — углом максимального возможного отклонения полной реакции Pτp опорной поверхности от нормали к ней.

Если мы будем поворачивать силу P вокруг этой нормали, то также будут поворачиваться сила трения и полная реакция. При этом полная реакция опишет конус с осью, нормальной к поверхности соприкосновения тел, и с углом при вершине, равным удвоенному углу трения. Этот конус, называемый конусом трения, является геометрическим местом всевозможных направлений полной реакции R_тр.

Пусть к телу, лежащему на негладкой поверхности, весом которого можно пренебречь (рис. 64, б), приложена сила Р, составляющая угол β с нормалью к этой поверхности, как показано на чертеже. Убедимся, что сила P не может привести тело в движение, если угол β меньше угла трения α_тр. Разложим силу P на две составляющие:

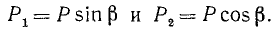
Составляющая P₁ стремится привести тело в движение, a P₂ давит на поверхность, вследствие чего возникает сила трения F_тр, направленная против составляющей P₁. Движение тела под действием силы P произойдет лишь в том случае, если составляющая P₁ будет больше максимально возможного значения силы трения:

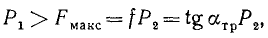
или, принимая во внимание предыдущие равенства,

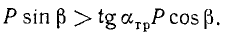
Деля обе части неравенства на P cos β, получим следующее необходимое условие движения тела:

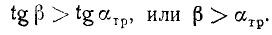
В это условие не входит значение силы P и надо сделать такое заключение: если на тело, лежащее на негладкой плоскости, оказывает давление сила, линия действия которой лежит внутри конуса трения, то, сколь бы велика ни была такая сила, она не приведет тело в движение.

Этим правилом широко пользуются в технике, на нем построены теория клина, теория самоторможения и др.

Рис. 65

Задача №12

Идеально сыпучее тело, лежащее на горизонтальной плоскости, принимает форму конуса. Определить угол наклона образующей к горизонтальной плоскости (угол естественного откоса).

Решение. Рассмотрим равновесие какой-либо частицы M (рис. 65), находящейся на поверхности конуса. На частицу действуют

1) вес G, направленный по вертикали вниз;
2) реакция/? соседних частиц сыпучего тела, направленная перпендикулярно возможному перемещению частицы и равная нормально му давлению частицы на поверхность конуса;
3) сила трения Fтр=fN, направленная по образующей вверх. Многоугольник (треугольник) сил, действующих на частицу, должен быть замкнут, так как она находится в равновесии и

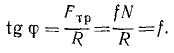
Но коэффициент трения, как известно, равен тангенсу угла трения, следовательно, угол естественного откоса равен углу трения:

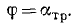
Угол естественного откоса, называемый также углом ската, имеет большое значение при проектировании различных насыпей, элеваторов, овощехранилищ и пр.

Задача №13

Сколько яровой пшеницы можно насыпать на круглую площадку диаметром 10 м, если вес 1 л яровой пшеницы равен 750 Г, а f =0,75?

Решение. Умножив насыпной вес яровой пшеницы 0,75 Т/м3 на объем конуса 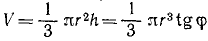, где φ—угол естественного откоса, получим ответ.
Ответ. 98 T.

Задача №14

Лестница AB (рис. 66) прислонена к стене под углом 30°. По лестнице поднимается человек весом P. Пренебрегая весом лестницы, определить наибольшее расстояние ВС, на которое может подняться человек, не уронив лестницы, если коэффициент трения лестницы о пол и о стену f = tg 15°.

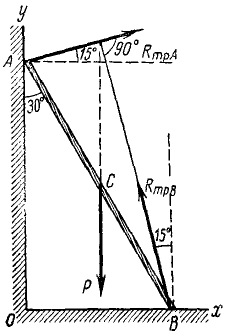
Рис. 66

Решение. Рассмотрим равновесие лестницы в предельном положении. На лестницу действуют: 1) вес P человека, приложенный в точке С; 2) полная реакция Rтр.А в точке А, направленная вправо н вверх под углом 90° —15° = 75° к стене, так как в предельном положении она составляет с идеальной реакцией угол, равный углу трения; 3) полная реакция R_тр.B в точке В, направленная вверх и влево под углом 75° к полу. Уравнения равновесия имеют вид:

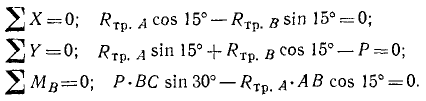
Определив R_тр.B из первого уравнения, подставим во второе:

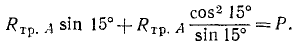
Умножив это уравнение на sin 15°, найдем, что R_тр.А = P sin 15°, и, подставляя это значение в третье уравнение равновесия, получим

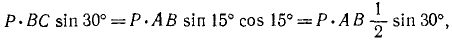
откуда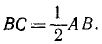

Если человек поднимается по лестнице выше AB/2, то три силы, действующие на лестницу, не пересекутся в одной точке, и необходимое условие равновесия трех непараллельных сил (см. § 3) будет нарушено. Если же человек будет находиться на лестнице ниже, то равновесие сохранится, так как угол трения является максимальным углом, который может составлять полная реакция с идеальной реакцией. В этом случае сила трения будет меньше произведения коэффициента трения на нормальное давление, и три приложенные к лестнице силы пересекутся в одной точке.

Момент пары, противодействующей качению тела по опорной поверхности, называют моментом трения качения.

Трение качения

В различных задачах механики надо учитывать трение, возникающее при качении тел. Оно не может быть объяснено в механике абсолютно твердого тела, а потому мы коснемся его лишь в общих чертах.

Пусть перпендикулярно к оси цилиндрического катка (рис. 67) веса G и радиуса r, лежащего на негладкой горизонтальной поверхности, приложена горизонтальная сила 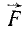. Вследствие деформаций катка и опорной поверхности их касание происходит не в одной точке, а по некоторой площадке, и нормальная реакция 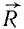бывает смещена относительно вертикальной плоскости симметрии катка на некоторое расстояние δ. В направлении, обратном силе 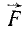, в том месте, где каток касается опорной поверхности, возникает сила 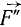, которую называют силой трения качения. Во время равновесия катка эта сила по модулю равна F и составляет с ней пару 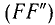, уравновешиваемую парой (GR), момент которой называют моментом трения качения. Плечо δ этой пары при предельном равновесии называют коэффициентом трения качения. Отметим, что в отличие от безразмерного коэффициента трения скольжения коэффициент трения качения имеет размерность длины и его выражают в миллиметрах, поэтому оба эти коэффициента — величины несравнимые. Неправильно было бы считать, что трение качения всегда меньше, чем трение скольжения. Они зависят от свойства трущихся тел. Летом ездят на колесах, а зимой на санях.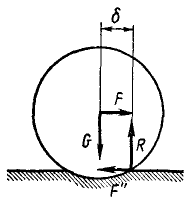

Рис. 67

Момент трения качения вполне это трение характеризует, но иногда бывает удобно пользоваться силой трения качения, величину которой

(40)

легко получить из равенств моментов двух пар.

Рекомендую подробно изучить предмет:

Теоретическая механика

Ещё лекции с примерами решения и объяснением:

• Естественный и векторный способы определения движения точки
• Координатный способ определения движения точки
• Касательное и нормальное ускорения точки
• Основные законы динамики
• Условия равновесия системы сходящихся сил в аналитической форме
• Приведение двух параллельных сил к равнодействующей
• Пара сил в теоретической механике
• Приведение системы сил к данной точке

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Теорема о параллельном переносе силы. Главный вектор и главный момент произвольной системы сил

Теорема о параллельном переносе силы. Главный вектор и главный момент произвольной системы сил

Теорема. Не изменяя действия силы на абсолютно твердое тело, ее можно перенести параллельно начальному положению в любую точку тела, прилагая при этом пару, момент которой равен моменту переносимой силы относительно той точки, куда сила переносится.

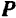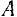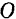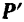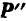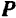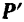Доказательство. Пусть мы имеем силу , приложенную в точке тела (рис. 46). Возьмем произвольную точку тела и приложим к ней две противоположно направленные силы и , параллельные и равные по модулю силе . Так как силы и взаимно уравновешиваются, то полученная система трех сил , и 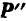эквивалентна одной силе 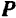. Сила 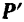может рассматриваться как сила 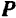, перенесенная параллельно ее начальному положению, а силы 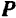и образуют пару. Момент этой пары (рис. 46) равен моменту силы 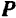относительно той точки 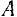, в которую сила переносится. Теорема доказана.

Рассмотрим примеры, иллюстрирующие эту теорему.

действию на него силы , растягивающей брус, и пары , изгибающей брус. Модуль момента этой пары равен .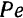

Теорема о параллельном переносе силы лежит в основе весьма плодотворного метода Пуансо, позволяющего приводить к одной точке (с добавлением соответствующих пар) любую систему произвольно расположенных сил. Пусть на твердое тело действует система нескольких, например, трех, сил 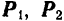и 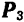, расположенных как угодно в пространстве. Возьмем произвольную точку 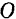и перенесем в нее, пользуясь теоремой Пуансо, все силы системы. В результате мы получим (рис. 48, о) пространственную систему сил и , приложенных

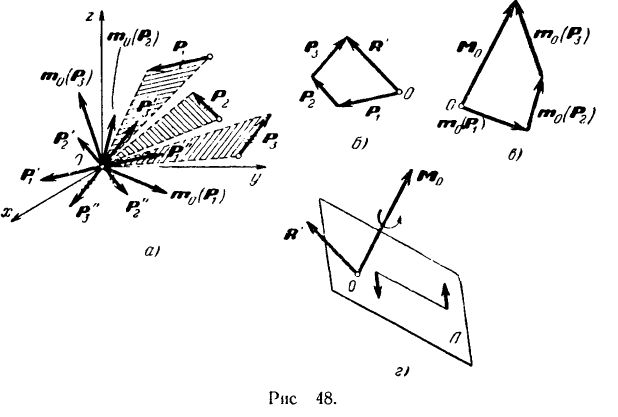
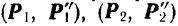к одной точке , и пространственную систему присоединенных пар и 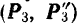. Для наглядности на рис. 48, а векторы сил присоединенных пар перечеркнуты соответственно одной, двумя и тремя черточками.

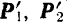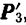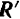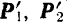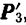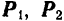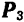Приложенные к одной точке силы и мы можем сложить по правилу векторного многоугольника (рис. 48,6) и, следовательно, заменить одной, эквивалентной им, силой . Так как силы и соответственно равны силам и , то

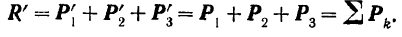
Как мы уже говорили ранее (стр. 38), вектор 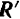, равный геометрической сумме всех сил данной системы, называется главным вектором этой системы.

Пары, расположенные как угодно в пространстве, также можно сложить и заменить одной результирующей парой, момент которой равен геометрической сумме моментов составляющих пар. Момент каждой из пар, присоединяемой при переносе сил в одну точку, равен моменту соответствующей силы относительно этой точки.

Произвольная гонка тела, в которую мы переносим параллельно самим себе все силы системы, называется центром приведения. Можно, следовательно, сказать, что момент результирующей пары равен геометрической сумме моментов всех сил системы относительно центра приведения.

Геометрическая сумма моментов всех сил системы относительно какой-либо точки называется главным моментом данной системы сил относительно этой точки.

Обозначая главный момент системы сил относительно какой-либо точки 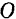символом 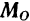, будем иметь:

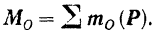
Изображая (рис. 48,о) моменты сил системы относительно выбранного центра 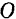приведения векторами и 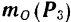, построенными в соответствии с установленным в предыдущем параграфе правилом, мы можем затем сложить их по способу векторного многоугольника (рис. 48, б) и тем самым найти главный момент 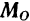данной системы сил относительно точки 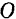, т. е. момент результирующей пары.

Таким образом, мы приходим к следующему выводу: любая система сил эквивалентна по своему действию на абсолютно твердое тело совокупности: одной силы 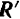, равной главному вектору данной системы и приложенной в произвольной точке тела (в центре приведения), и одной пары, момент которой равен главному моменту 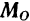данной системы сил относительно выбранного центра приведения (рис. 48,г).

Модуль и направление главного вектора системы не зависит от выбора центра приведения, так как все силы переносятся в центр приведения параллельно самим себе, и силовой многоугольник во всех случаях будет одним и тем же. Наоборот, модуль и направление главного момента зависят, вообще говоря, от выбора центра приведения, так как с изменением центра приведения изменяются модули и направления моментов сил

системы относительно этого центра, а следовательно, и их геометрическая сумма. Поэтому когда говорят о главном моменте данной системы сил, то всегда указывают, относительно какой точки он определяется.

Установив общие понятия момента пары и момента силы относительно точки, а также способ приведения произвольной системы сил к одному центру, мы перейдем сейчас к рассмотрению частного случая, когда все силы системы лежат в одной плоскости.

По чисто методическим соображениям, более детальное рассмотрение общего случая произвольной пространственной системы сил будет сделано в главе VII.

Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:

Возможно вам будут полезны эти дополнительные темы:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

[spoiler title=”источники:”]

http://www.evkova.org/sistema-sil-na-ploskosti-v-teoreticheskoj-mehanike

http://lfirmal.com/teorema-o-parallelnom-perenose-silyi-glavnyij-vektor-i-glavnyij-moment-proizvolnoj-sistemyi-sil/

[/spoiler]

В число сил и моментов, входящих в уравнения (12.1), включаются реакции и моменты реакций в кинематических парах группы.  [c.104]

Составляем и решаем уравнения равновесия отдельных звеньев. Уравнения равновесия колеса / (рис. 62. б). К колесу приложены уравновешивающий момент Му = 4 нм, направленный в сторону, противоположную моменту реакция Pji стороны колеса 2 на колесо 1, направленная под углом а = 20 к касательной к начальной окружности колеса 1, и реакция в шарнире А, приложенная к его оси. Уравнением равновесия колеса 1 будет  [c.109]

Реакции опор определяют из уравнения равновесия, сумма моментов внешних сил относительно рассматриваемой опоры и момента реакции в другой опоре равна нулю.  [c.101]

Момент реакции нити 5 относительно оси Оуу  [c.151]

На волчок действуют внешние силы сила тяжести G и реакция опоры О. Так как момент реакции опоры относительно точки О равен нулю, то главный момент внешних сил относительно  [c.249]

Ц Ti X / ,= S Мш = Мо — главный момент реакций связей относительно центра О  [c.284]

Вал I с колесом 1 (рис. 213,6). На этот вал действуют вес “Pi, пара сил с моментом реакция подшипника 7 и реакция колеса 2. Реакция подшипника, если пренебречь его раз-  [c.110]

Однородный брус АВ длины I и веса Р шарнирно крепится на конце А и свободно опирается на цилиндр радиусом г в точке К, образуя угол а с горизонтом. Пренебрегая трением, указать, чему равен момент реакции Ra относительно точки D пересечения линии действия силы тяжести Р и радиальной прямой ОК, Трением пренебречь.  [c.7]

Невесомая трехшарнирная арка нагружена горизонтальной силой f =10 кН. Определить момент реакции  [c.8]

Момент реакции N можно находить или как произведение N на плечо h = 2l os а, или же можно представить силу N разложенной вдоль АВ и по нормали к АВ на составляющие Vi, и искать mom N по теореме Вариньона mom N = mom + mom N . При этом mom N = 0 и мы получим mom /if = mom iVj = 2/ Л/ os а. Такой прием бывает особенно удобен в случаях, когда возникают затруднения с подсчетом плеча.  [c.250]

Момент реакции опоры N относительно точки О равен нулю. Следовательно, скорость конца вектора кинетического момента будет всегда перпендикулярна векторам (Oi и о>2.  [c.195]

Момент, реакции. .. заделки. Момент пары сил. .. в заделке. Освобождение. .. от заделки.  [c.24]

Однородный стержень массой 8 кг колеблется в вертикальной плоскости. В некоторый момент времени его точки А и В имеют ускорения ai = 3 м/с , Д2 = 6 м/с . Определить в этот момент реакцию правой пружины. Размеры /, = 1 м, /2 = 0,3 м. (84,6)  [c.295]

В этих уравнениях отдельно выписаны проекции и моменты реакций и активных сил. Рассматривая уравнения (111.43), заключаем, что первые пять уравнений устанавливают зависимость между реакциями связей в точках Л и В и активными силами. В шестое уравнение входят лишь активные силы. Следовательно, это уравнение и есть искомое условие равновесия. Формулируется это условие равновесия так несвободное твердое тело с двумя закрепленными точками или неподвижной осью) находится в равновесии, если алгебраическая сумма моментов активных сил относительно неподвижной оси равна нулю.  [c.293]

Замечания о главном моменте реакций внутренних связей  [c.64]

Можно доказать, что главный момент реакций идеальных внутренних связей относительно произвольной точки равен нулю. Действительно, из условия (1.21) для возможных перемещений, которые оставляют точки системы на связях, имеем  [c.64]

Если пренебречь силами сопротивления воздуха и моментом трения в оси, то внешними силами, приложенными к телу, будут реакция оси и сила тяжести G. Но момент реакции относительно оси подвеса равен нулю, момент же силы тяжести равен — Gs sin ф. Дифференциальное уравнение вращения тела принимает вид  [c.179]

Последнее соотношение показывает, что в настоящем случае множитель к пропорционален составляющей момента М реакций шарниров ио оси веду-щего вала. Сам же момент М, так же как и моменты реакций подшипников Л1( и М2, остается пока неопределенным.  [c.335]

При ф = О, Я.. .. имеем М = —М,и = —Л1,, т. е. момент реакций равен по величине и противоположен по направлению задаваемому моменту Л1, при (j) = я/2, Зя/2,. .., согласно (83), момент пары реакций, приложенной к вилке ведомого вала, будет равен —М = (M,/ os а) = МгК, т. е. одинаков по величине и противоположен по направлению моменту полезного сопротивле-  [c.336]

Таким образом, все моменты реакций определены как по величине, так и по направлению. Легко проверить, что условия ортогональности моментов М , Л1[, Л12 соответствующим осям ОЛ, и ОВи 0,0 и ОО2 выполняются.  [c.336]

Ось Су совпадает с осью вращения наружного кольца пренебрегая трением, имеем поэтому = и наоборот, /п< с) 0 уак как к внутреннему кольцу должен быть приложен некоторый момент реакций относительно оси Сх, чтобы предотвратить вращение кольца вокруг этой оси. Величина этого момента (здесь и далее массами колец пренебрегаем) определяется по первому уравнению (44)  [c.618]

Угловая скорость собственного вращения не вошла в это уравнение она войдет в первое уравнение (104), в правую часть которого следует внести добавочное слагаемое, выражающее момент реакции паза, который из этого уравнения и определится.  [c.626]

Так как моменты реакций и подпятника А и подшипника В относительно оси 2 также равны нулю.  [c.612]

Здесь L, М, N обозначают проекции результирующего момента системы заданных сил Fv относительно начала координат проекции момента реакции вычислялись по известному правилу из матрицы  [c.59]

Моменты реакций подшипника и подпятника, а также сил Р относительно оси 2 равны нулю, так как линии действия этих сил пересекают ось сумма моментов внешних сил относительно оси вращения называется вращающим моментом. Тогда  [c.158]

Прикладываем в сечении А пару сил с моментом, равным единице (единичный момент). Реакции опор от этого момента показаны на рис. 7-5, д. Уравнения единичного момента на первом и втором участках  [c.143]

Условие для определения наивыгоднейшей длины консоли записывается так Мо 1 = Л тах-Найдем эти моменты. Реакции опор будут  [c.99]

При этом все материальные точки тела Т создают моменты реакций, действующие вокруг осей х я у  [c.23]

Уравнения (VI.11) полностью совпадают с уравнениями (VI.4), полученными с использованием обобщенных уравнений Эйлера. При составлении уравнений движения сложных гироскопических систем при помощи обобщенных уравнений Эйлера оказывается необходимым для согласования дифференциальных уравнений движения отдельных элементов системы определять моменты реакций связей между элементами с использованием принципа Д Аламбера (такие примеры даются в гл. VII).  [c.126]

В ряде случаев нахождение моментов реакций связей может оказаться достаточно сложным, так как требует глубокого проникновения в физику явлений, происходящих при движении всех элементов системы.  [c.126]

Выполняют расчеты валов на статическую прочность и на сопротивление усталости. Расчет проводят в такой последовательности по чертежу сборочной единицы вала составляют расчетную схему, на которую наносят все внешние силы, нагружающие вал, приводя плоскости их действия к двум взаимно перпендикулярным плоскостям (горизонтальной X и вертикальной У). Затем определяют реакции опор в гбризонтальной и вертикальной плоскостях. В этих же плоскостях строят эпюры изгибающих моментов Мх Му, отдельно эпюру крутящего момента Предположительно устанавливают опасные сечения исходя из эпюр моментов, размеров сечений вала и концентраторов напряжений (обьршо сечения, в которых приложены внешние силы, моменты, реакции опор или места изменений сечения вала, нагруженные моментами). Проверяют прочность вала в опасных сечениях.  [c.165]

Нагрузки от момента (реакции Fri, Ft2, , гг) распределяются по болтам пропорционально их деформациям при повороте кронштей-  [c.38]

Определим, какие внешние силы действуют на раму при этом вращении По теореме Резаля главный момент внеиншх сил Л с относительно точки С геометрически равен скорости и. На раму с укрепленным в ней маховиком действуют внешние силы сила тяжести G гироскопа и реакции подшипников Л и S, в которых находится ось рамы. Сила тяжести G, приложенная в точке С, не имеет относительно нее момента, и, следовательно, главный момент внешних сил Мс представляет собой суммарный момент реакций ПОДИ]КИННКОВ.  [c.251]

Невесомая плоская конструкция находится в равновесии под действием пары сил с моментом М. Определить момент реакции Re относительно точки А, если AB = B = D=DE,AB ,B , DA DE.  [c.11]

Реакции в заделке. Заделкой называется жесткое (неподвижное) соединение звеньев. Их взаимодействие сводится к силе и моменту реакции. На рис. 5.4,5 показана заделка в неподвижной стенке стержня, на который действует плоская система сил / 1 и РРеакцию удобно представить в виде двух составляющих и силы и реактивного момента М.  [c.56]

На поворачиваемый вокруг ребра D массив действуют вес и реакция в ребре D. Момент реакции относительно оси вращения равен нулю, следовательно, равна нулю и работа реакции. Момент веса — величина переменная — равен произведе-дению силы 4 7″ на плечо D os ф, где ф (см. рис. 211, б) —угол, составляемый D с горизонтальной плоскостью  [c.372]

Теорема 5.1.5. Пусть после освобоок.дения от некоторых связей оставшиеся связи идеальны и допускают дифференциал вращения вокруг произвольной оси. Тогда производная по времени от вектора кинетического момента равна сумме моментов внешних активных сил, включая моменты реакций удаленных связей  [c.386]

НИИ звена 2 относительно звена / линия действия реакций и смещается относительно центра пары на Д. Она должна быть касательной к кругу трения чтобы определить ее направление, пользуются следующим правилом направление момента реакции (Нц) относительно центра О должно совпадать с направлениеТи относительной угловой скорости с тем же индексом ( oji). Использование угла трения и круга трения часто облегчает силовой анализ механизмов.  [c.45]

Составлениё дифференциальных уравнений движения сложной гироскопической системы с помощью второго метода Лагранжа не требует отыскания моментов реакций связей и, следовательно, глубокого анализа физики явлений, происходящих при движении системы, а сводится к выполнению ряда формальных математических преобразований.  [c.126]

Отклонение оси z ротора гироскопа в результате его прецессии вокруг оси наружной рамки карданова подвеса, порождаемой моментом реакций в опорах карданова подвеса, оказывается ограниченным и достигает величины о t M. (VI.52 а)]. При этом направление отклонения aS гироскопа не зависит от знака момента Му внешних сил и при периодическом действии моментов Муу внешних сил разного знака отклонение оси z ротора гироскопа неизменно нарастает. Если диссипативными моментами  [c.147]

---

Правила знаков для внешних сил, моментов, внутренних силовых факторов, напряжений и перемещений принятые в сопромате, теоретической и технической механике при решении задач.

Правила знаков для внутренних силовых факторов

При растяжении-сжатии

Внутренняя продольная сила N, которая стремится растянуть рассматриваемую часть бруса, считается положительной. Сжимающая продольная сила имеет отрицательный знак.

Положительное направление внутренней продольной силы N

Видео по правилам знаков:

Другие видео

При кручении

Внутренний скручивающий момент T считается положительным, если он стремится повернуть рассматриваемую часть бруса против хода часовой стрелки, при взгляде на него со стороны внешней нормали.

Положительное направление внутреннего скручивающего момента T

При изгибе

Внутренняя поперечная сила Q считается положительной, в случае, когда она стремится повернуть рассматриваемую часть бруса по ходу часовой стрелки.

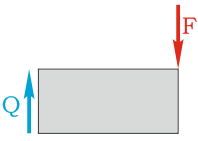
Положительное направление внутренней поперечной силы Q

Внутренний изгибающий момент M положителен, когда он стремится сжать верхние волокна бруса.

Положительное направление внутреннего изгибающего момента M

Примечание: Величина и знак внутренних сил и моментов зависит от вызывающих их внешних усилий, поэтому указанные правила знаков в том же виде справедливы и для внешних нагрузок.

Правило знаков при внецентренном нагружении

Положительными принимаются внешние усилия стремящиеся вызвать растяжение первой четверти сечения.

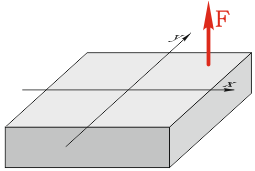
Положительное направление действия внешних нагрузок

Правила знаков для напряжений

Нормальные напряжения σ положительны, если они растягивают выделенный элемент бруса.

Положительные нормальные напряжения

Касательные напряжения τ будут положительными, если они стремятся повернуть рассматриваемый элемент бруса по ходу часовой стрелки.

Положительные касательные напряжения

Правило знаков для деформаций и перемещений

Деформация при растяжении-сжатии Δl считается положительной, если длина стержня при этом увеличивается.

Положительная деформация при продольном нагружении

При плоском поперечном изгибе

Вертикальное перемещение сечения бруса принимается положительным, если оно направлено вверх от начального положения.

Положительные перемещения сечений балки при изгибе

Правило знаков при составлении уравнений равновесия

Для проекций сил на оси системы координат

Проекции внешних сил на оси системы координат принимаются положительными, если их направление совпадает с положительным направлением соответствующей оси.

Для моментов

Сосредоточенные моменты и моменты сил в уравнениях статики записываются с положительным знаком, если они стремятся повернуть рассматриваемую систему против хода часовой стрелки.

Правило знаков при составлении уравнений статики для неподвижных систем

При составлении уравнений равновесия статичных (неподвижных) систем (например, при определении опорных реакций), последние два правила упрощаются до вида:

Проекции сил и моменты, имеющие одинаковое направление записываются с одинаковыми знаками, соответственно проекции сил и моменты обратного направления – с противоположными.

Метод сечений >
Примеры решения задач >

Энергетика химических процессов

Общая химия. Учебное пособие — Таирова А.Р., Кузнецов А.И. — 2005

• 5.1. Общие понятия
• 5.2. Внутренняя энергия. Первый закон термодинамики
• 5.3. Энтальпия системы. Тепловые эффекты химических реакций
• 5.4. Термохимические расчеты
• 5.5. Химическое сродство. Энтропия химических реакций. Энергия Гиббса
• 5.6. Второй и третий законы термодинамики

Глава 5 . Энергетика химических процессов

Науку о взаимных превращениях различных видов энергии называют термодинамикой. Термодинамика устанавливает законы этих превращений, а также направление самопроизвольного тече­ния различных процессов в данных условиях.

5.1. Общие понятия. При протекании химических реакций изменяет­ся энергетическое состояние системы, в которой идет эта реакция. Состояние системы характеризуется термодинамическими парамет­рами (р, Т, с и др.). При изменении параметров меняется и состояние системы. В термодинамике свойст­ва системы рассматриваются при ее равновесном состоянии. Термодинамическое состояние системы называют равновесным в том случае, когда его термодинамические параметры одинаковы во всех точках системы и не изменяются самопроизвольно (без затраты работы) во времени. Термодинамика изучает переходы системы из одного состояния в другое. Но переходы должны осуществляться при термодинамическом равновесии с окружающей средой, т.е. очень медленно, а в идеале — бесконечно медленно. При этом могут изменяться все параметры состояния системы, либо некоторые параметры остаются без изменения. Если процессы перехода системы происходят при постоянстве каких-то параметров системы, то они называются:

а) изобарическими (р = const);

б) изохорическими (Т= const);

в) изотермическими (Т = const);

г) изобарно-изотермическими (р,T — const) и т.д.

Термодинамика изучает возможность или невозможность самопроизвольного перехода системы из одного состояния в другое и энергетические эффекты этих переходов. Скорость и механизм про­цессов перехода — это области химической кинетики.

5.2. Внутренняя энергия. Первый закон термодинамики. При химических реакциях происходят глубокие качественные изменения в системе, рвутся связи в исходных веществах и возникают новые связи в конечных продуктах. Эти изменения сопровождаются поглощением или выделением энергии. В большинстве случаев этой энергией является теплота. Раздел термодинамики, изучающий тепловые эффекты химических реакций, называют термохимией. Реакции, которые сопровож­даются выделением теплоты, называют экзотермическими, а те, которые сопровождаются поглощением теплоты, — эндотер­мическими. Теплота реакции является, таким образом, мерой изменения свойств системы, и знание ее может иметь большое значение при определении условий протекания той или иной реакции.

При любом процессе соблюдается закон сохранения энергии как проявление более общего закона природы — закона сохранения материи. Теплота Q, поглощенная системой, идет на изменение ее внутренней энергии и на совершение работы А:

Q = ∆U + A

Количественное соотношение между изменением внутренней энергии, теплотой и работой устанавливает первый закон термодинамики:

Q = ∆U + W

Уравнение означает, что теплота, подведенная к системе, расходуется на приращение внутренней энергии системы и на работу системы над окружающей средой.

Внутренняя энергия системы U — это общий ее запас, включающий энергию поступательного и вращательного движений молекул, энергию внутримолекулярных колебаний атомов и атомных групп, энергию движения электронов, внутриядерную энергию и т.д. Внутренняя энергия — полная энергия системы без потенциальной энергии, обусловленной положением системы в пространстве, и без кинетической энергии системы как целого. Абсолютное значение внутренней энергии U веществ неизвестно, так как нельзя привести систему в состояние, лишенное энергии. Внутренняя энергия, как и любой вид энергии, является функцией состояния, т.е. ее изменение одно­значно определяется начальным и конечным состояниями системы и не зависит от пути перехода, по которому протекает процесс:

U=U₂-U₁,

где: U — изменение внутренней энергии системы при переходе из начального состояния U₁ в конечное U₂. Если U₂ > U₁, то U> 0.

Если U₂< U₁, то U< 0.

5.3. Энтальпия системы. Тепловые эффекты химических реакций. Теплота Q и работа A функциями состояния не являются, ибо они служат формами передачи энергии и связаны с процессом, а не с состоянием системы. При химических реакциях А — это работа против внешнего давления, т.е. в первом приближении

А = рV,

где V — изменение объема системы (V₂ – V₁).

Так как большинство химических реакций проходит при постоянном давлении, то для изобарно-изотермического процесса (р = const, Т= const) теплота Q_p будет равна:

Qp = ∆U + p∆V,

Qp= (U₂ – U₁) + p(V₂ – V₁)

Qp = (U₂ + pV₂) – (U₁ + pV₁)

Сумму U+ pV обозначим через Н, тогда

Qp = H₂ – H₁ = ∆H

Величину Н называют энтальпией. Таким образом, теплота при р=const и Т=const приобретает свойство функции состояния и не зависит от пути, по которому протекает процесс. Отсюда теплота реакции Q_p в изобарно-изотермическом процессе равна изменению энтальпии системы Н (если единственным видом работы является работа расширения):

Qp = ∆H

Энтальпия, как и внутренняя энергия, является функцией состояния: ее изменение (H) определяется только начальным и конечным состояниями системы и не зависит от пути перехода. Нетрудно видеть, что теплота реакции в изохорно-изотермическом процессе (V= const; Т = const), при котором V=0, равна изменению внутренней энергии системы:

Qv = ∆U

Теплоты химических процессов, протекающих при р, Т=const и V, Т=const, называют тепловыми эффектами.

При экзотермических реакциях энтальпия системы умень­шается и Н < 0 (Н₂ < H₁), а при эндотермических энтальпия системы увеличивается и Н > 0 (Н₂ > Н₁). В дальнейшем теп­ловые эффекты всюду выражаются через H.

5.4. Термохимические расчеты. Термохимические расчеты основаны на законе Гесса, позволяющее рассчитать энтальпию химической реакции: тепловой эффект реакции зависит только от природы и физического состояния исходных веществ и конечных продуктов, но не зависит от пути перехода.

Часто в термохимических расчетах применяют следствие из закона Гесса: тепловой эффект реакции (Н_x.p.) равен сумме теплот образования Н_обр продуктов реакции за вычетом суммы теплот образования исходных веществ с учетом коэффициентов перед формулами этих веществ в уравнении реакции:

∆Hx.p. = ∑∆H_обр^прод — ∑∆H_обр^исх (1)

Пример 1. При взаимодействии кристаллов хлорида фосфора (V) с парами воды образуется жидкий РОС1₃ и хлороводород. Реакция сопровождается выделением 111,4 кДж теплоты. Напи­шите термохимическое уравнение этой реакции.

Решение. Уравнения реакций, в которых около символов химических соединений указываются их агрегатные состояния или кристаллическая модификация, а также числовое значение тепло­вых эффектов, называют термохимическими. В термохимических уравнениях, если это специально не оговорено, указываются значения тепловых эффектов при постоянном давлении Qp, равные изменению энтальпии системы Н. Значение Н приводят обычно в правой части уравнения, отделяя его запятой или точкой с запятой. Приняты следующие сокращенные обозначения агрегат­ного состояния вещества: г — газообразное, ж — жидкое, к — крис­таллическое. Эти символы опускаются, если агрегатное состояние веществ очевидно.

Если в результате реакции выделяется теплота, то Н < 0. Учитывая сказанное, составляем термохимическое уравнение данной в примере реакции:

PCl₅(к) + H₂O(г) = POCl₃(ж) + 2HCl(г); ∆Hx.p.= -111,4 кДж

Таблица 15.

Стандартные теплоты (энтальпии) образования

некоторых веществ

Вещество	Состояние	кДж/моль	Вещество	Состояние	кДж/моль
С2Н2	г	+226,75	СО	г	-110,52
CS2	г	+115,28	СН3ОН	г	-201,17
NO	г	+90,37	С2Н5OН	г	-235,31
С6Н6	г	+82,93	H2O	г	-241,83
С2Н4	г	+52,28	Н2О	ж	-285,84
H2S	г	-20,15	NH4C1	к	-315,39
NН3	г	-46,19	СО2	г	-393,51
СН4	г	-74,85	Fе2О3	к	-822,10
С2Н6	г	-84,67	TiO2	к	-943,90
НС1	г	-92,31	Са(ОН)2	к	-986,50
			А12O3	к	-1669,80

Пример 2. Реакция горения этана выражается уравнением:

С₂Н₆(г) + 3¹/₂О₂= 2СО₂(г)+3Н₂О(ж); ∆Hх.р.= -1559,87 кДж

Вычислите теплоту образования этана, если известны теплоты образования СO₂(г) и Н₂O(ж) (см. табл. 15).

Решение. Теплотой образования (энтальпией) данного соединения называют тепловой эффект реакции образования 1 моль этого соединения из простых веществ, взятых в их устойчивом состоянии при данных условиях.

Обычно теплоту образования относят к стандартному состоянию, т.е. 25° С (298 К) и 1,01310⁵ Па и обозначают через.Так как тепловой эффект с температурой изменяется незначительно, то в дальнейшем индексы опускаются и тепловой эффект обозначается через Н. Следовательно, нужно вычислить тепловой эффект реакции, термохимическое уравнение которой имеет вид

2С(графит)+3Н₂(г) = С₂Н₆(г); ∆H = ?

исходя из следующих данных:

а) С₂Н₆(г) + 3¹/₂О₂(г)=2СО₂(г)+3Н₂О(ж); ∆H =-1559,87 кДж

б) 2С(графит)+О₂(г)= СО₂(г); ∆H =-393,51 кДж

в) Н₂(г)+ ¹/₂О₂=Н₂О(ж); ∆H =-285,84 кДж

На основании закона Гесса с термохимическими уравнениями можно оперировать так же, как и с алгебраическими. Для получения искомого результата следует уравнение (б) умножить на 2, уравнение (в) — на 3, а затем сумму этих уравнений вычитают из уравнения (а):

С₂Н₆ + 3¹/₂О₂-2С-2О₂-3Н₂—³/₂О₂=2СО₂+3Н₂О-2СО₂-3Н₂О

∆H =-1559,87-2(-393,51)-3(-285,84)= +84,67 кДж;

∆H =-1559,87+787,02+857,52;

С₂Н₆=2С+3Н₂; ∆H = +84,67 кДж

Так как теплота образования равна теплоте разложения с обратным знаком, то .

К тому же результату придем, если для решения задачи применить вывод из закона Гесса:

∆Hх.р. =2∆Hсо₂+3∆Hн₂о-∆Hс₂н₆-31/2∆Hо₂

Учитывая, что теплоты образования простых веществ условно приняты равными нулю

∆Hс₂н₆=2∆Hсо₂+3∆Hн₂о-∆Hх.р.

∆Hс₂н₆=2(-393,51)+3(-258,84)+1559,87=-84,67;

∆H^обрс₂н_6(г)=-84,67 кДж

Пример 3. Реакция горения этилового спирта выражается термохимическим уравнением

С₂Н₅ОН(ж)+3О₂(г)=2СО₂(г)+3Н₂О(ж); ∆H=?

Вычислите тепловой эффект реакции, если известно, что молярная теплота парообразования С₂Н₅OН(ж) равна +42,36 кДж, а теплоты образования С₂Н₅OН(г), СO₂(г), Н₂O(ж) см. табл. 15.

Решение. Для определения Н реакции необходимо знать теплоту образования С₂Н₅OН(ж). Последнюю находим из данных:

С₂Н₅ОН(ж) = С₂Н₅ОН(г); ∆H = + 42,36 кДж

+42,36 = — 235,31- ∆Hс₂н₅он (ж);

∆Hс₂н₅он (ж) = — 235,31-42,36 = -277,67 кДж

Вычисляем H реакции, применяя следствие из закона Гесса:

∆Hх.р.=2(-393,51)+3(-285,84)+277,67=-1366,87 кДж

5.5. Химическое сродство. Энтропия химических реакций. Энергия Гиббса. Самопроизвольно могут протекать реакции, сопровождаю­щиеся не только выделением, но и поглощением теплоты.

Реакция, идущая при данной температуре с выделением теплоты, при другой температуре проходит с поглощением теплоты. Здесь проявляется диалектический закон единства и борьбы противоположностей. С одной стороны, система стремится к упорядочению (агрегации), к уменьшению Н; с другой стороны, система стремится к беспорядку (дезагрегации). Первая тенденция растет с понижением, а вторая — с повышением температуры. Тенденцию к беспорядку характеризует величина, которую называют энтропией.

Энтропия S, так же как внутренняя энергия U, энтальпия Н, объем V и др., является свойством вещества, пропорциональным его количеству. S, U, H, V обладают аддитивными свойствами, т.е. при соприкосновении системы суммируются. Энтропия отражает движение частиц вещества и является мерой неупорядоченности системы. Она возрастает с увеличением движения частиц: при нагревании, испарении, плавлении, расширении газа, при ослаблении или разрыве связей между атомами и т.п. Процессы, связанные с упорядоченностью системы: конденсация, кристаллизация, сжатие, упрочнение связей, полимеризация и т.п.— ведут к уменьшению энтропии. Энтропия является функцией состояния, т.е. ее изменение зависит только от начального (S₁) и конечного (S₂) состояний и не зависит от пути процесса:

Так как энтропия увеличивается с повышением температуры, то можно считать, что мера беспорядка равна TS. Энтропия выражается в Дж/(моль.К).

Таким образом, движущая сила процесса складывается из двух сил: стремления к упорядочению (Н) и стремления к беспорядку (TS). При р = const и Т = const общую движущую силу процесса, которую обозначают G, можно найти из соотношения

∆G=(H₂-H₁)-(TS₂-TS₁); ∆G=∆H-T∆S

где: величина G называется изобарно-изотермическим потенци­алом или энергией Гиббса.

Мерой химического сродства является убыль энергии Гиббса (G), которая зависит от природы вещества, его количества и температуры.

Энергия Гиббса является функцией состояния, поэтому

∆Gx.p.=∑ ∆G_oбp^прод-∑∆G_oбp^исх (3)

Самопроизвольно протекающие процессы идут в сторону уменьшения потенциала и, в частности, в сторону уменьшения G. Если G < 0, процесс принципиально осуществим; если G>0, процесс самопроизвольно проходить не может. Чем меньше G, тем сильнее стремление к протеканию данного процесса и тем дальше он от состояния равновесия, при котором G = 0 и H= TS.

Из соотношения G = H – TS видно, что самопроизвольно могут протекать и процессы, для которых H>0 (эндотерми­ческие). Это возможно, когда S>0, но |TS| > |H| и тогда G<0. С другой стороны, экзотермические реакции (H<0) самопроиз­вольно не протекают, если при S<0 окажется, что G>0.

5.6. Второй и третий законы термодинамики. Для систем, которые не обмениваются с окружающей средой ни энергией, ни веществом (изолированные системы), второй закон термодинамики имеет следующую формулировку: в изолированных системах са­мопроизвольно идут только такие процессы, которые сопровождаются возрастанием энтропии: AS > 0.

Второй закон термодинамики имеет статистический характер, т.е.
справедлив лишь для систем, состоящих из очень большого числа
частиц.

Однако, если в системе протекает химическая реакция, то система обменивается энергией с окружающей средой, т.е. не является изоли­рованной. Химические реакции обычно сопровождаются изменением как энтропии, так и энтальпии.

В отличие от других термодинамических функций, можно определить не только изменение, но абсолютное значение энтропии. Это вытекает из высказанного в 1911 г. М. Планком постулата, согласно которому «при абсолютном нуле энтропия идеального кристалла равна нулю». Этот постулат получил название третьего закона термодинамики.

Пример 1. В каком состоянии энтропия 1 моль вещества больше при одинаковой температуре: в кристаллическом или парообразном?

Решение. Энтропия есть мера неупорядоченности состояния вещества. В кристалле частицы (атомы, ионы) расположены упорядоченно и могут находиться лишь в определенных точках пространства, а для газа таких ограничений нет. Объем 1 моль газа гораздо больше объема 1 моль кристаллического вещества; возможность хаотичного движения молекул газа больше. А так как энтропию можно рассматривать как количественную меру хаотичности атомно-молекулярной структуры вещества, то энтропия 1 моль паров вещества больше энтропии 1 моль его кристаллов при одинаковой температуре.

Пример 2. Прямая или обратная реакция будет протекать при стандартных условиях в системе

СН₄(г)+СО₂ ↔ 2СО(г)+2Н₂(г)

Решение. ВычислимΔG⁰₂₉₈ прямой реакции. Значения ΔG⁰₂₉₈соответствующих веществ приведены в табл. 16. Зная, что ΔG есть функция состояния и что ΔG для простых веществ, находящихся в устойчивых при стандартных условиях агрегатных состояниях, равны нулю, находим ΔG⁰₂₉₈процесса:

∆G⁰₂₉₈ = 2 (-137,27) +2 (0) — (-50,79-394,38) = +170,63 кДж

То, что ΔG⁰₂₉₈> 0, указывает на невозможность самопроиз­вольного протекания прямой реакции при Т = 298К и давлении взятых газов равном 1,013 ∙ 10⁵ Па (760 мм рт. ст. = 1 атм).

Таблица 16

Стандартная энергия Гиббса образования ΔG⁰₂₉₈некоторых веществ

Вещество	Состояние	ΔG0298, кДж/моль	Вещество	Состояние	ΔG0298, кДж/моль
ВаСО3	к	-1138,8	FeO	к	-244,3
СаСО3	к	-1128,75	Н2О	ж	-237,19
Fе3O4	к	-1014,2	Н2O	г	-228,59
ВеСО3	к	-944,75	PbO2	к	-219,0
СаО	к	-604,2	СО	г	-137,27
ВеО	к	-581,61	СН4	г	-50,79
NaF	к	-541,0	NO2	г	+51,84
ВаО	к	-528,4	NO	г	+86,69
СО2	г	-394,38	C2H2	г	+209,20
NaCl	к	-384,03
ZnO	к	-318,2

Таблица17

Стандартные абсолютные энтропии ΔS⁰₂₉₈ некоторых веществ

Вещество	Состояние	ΔS0298, Дж/(моль.К)	вещество	Состояние	ΔS0298,Дж/(моль.К)
С	Алмаз	2,44	Н2O	г	188,72
С	Графит	5,69	N2	г	191,49
Fe	к	27,2	NН3	г	192,50
Ti	к	30,7	СО	г	197,91
S	Ромб	31,9	с2H2	г	200,82
TiO2	к	50,3	O2	г	205,03
FeO	к	54,0	H2S	г	205,64
H2O	ж	69,94	NO	г	210,20
Fе2О3	к	89,96	CO2	г	213,65
NH4C1	к	94,5	C2H4	г	219,45
СН3ОН	ж	126,8	Cl2	г	222,95
Н2	г	130,59	NO2	г	240,46
Fе3O4	к	146,4	РС13	г	311,66
СН4	г	186,19	PCl5	г	352,71
НС1	г	186,68

Пример 3. На основании стандартных теплот образования (см. табл. 15) и абсолютных стандартных энтропий веществ (табл.17) вычислите ΔS⁰₂₉₈ реакции, протекающей по уравнению

СО(г)+Н₂О(ж)=СО₂(г)+Н₂(г)

Решение. ∆G⁰ = ∆H⁰ — TS⁰; ∆H и ∆S – функции состояния, поэтому

∆Н⁰х.р.=∑ ∆Н⁰_прод — ∑ ∆Н⁰_исх ; ∆S⁰x.p.= ∑S⁰_прод — ∑ S⁰ _исх

∆Н⁰х.р.=(-393,51+0) – (110,52 – 285,84) = +2,85 кДж

∆S⁰x.p.=(213,65+130,59)-(197,91+69,94) = +76,39 = 0,07639 кДж/(моль∙К);

∆G⁰= +2,85 – 298 ∙ 0,07639 = — 19,91 кДж

Пример 4. Реакция восстановления Fе₂О₃ водородом протекает по уравнению

Fe₂O₃(к)+3H₂(г) = 2Fe(к)+3H₂O(г) ; ∆Н=+96,61 кДж

Возможна ли эта реакция при стандартных условиях, если изменение энтропии S=0,1387 кДж/(мольК)? При какой температуре начнется восстановление Fе₂О₃?

Решение. Вычисляем ∆G⁰ реакции:

∆G = ∆Н-Т∆S = 96,61 – 298 ∙ 0,1387 = +55,28 кДж

Так как ∆G > 0, то реакция при стандартных условиях невоз­можна; наоборот, при этих условиях идет обратная реакция окисления железа (коррозия). Найдем температуру, при которой∆G=0:

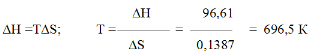
Следовательно, при температуре 696,5 К начнется реакция восстановления Fе₂О₃ Иногда эту температуру называют температурой начала реакции.

Пример 5. Вычислите ∆H⁰, ∆S и ∆G⁰ реакции, протекающей по уравнению

Fe₂O₃(к) + 3C = 2Fe + 3CO

Возможна ли реакция восстановления Fе₂О₃ углеродом при 500 и 1000 К?

Решение. ∆H⁰_xp и ∆S⁰_xp находим из соотношений (1) и (2) (см. разделы «Энергетика химических процессов. Термохимические расчеты» и «Химическое сродство»):

∆Н⁰x.p.= [3(-110,52)+2 ∙ 0] – [- 822,10 + 3 ∙ 0] = -331,56+822,10 = +490,54 кДж

∆S⁰x.p.=(2 ∙ 27,2+3 ∙ 197,91) – (89,96+3 ∙ 5,69) = 541,1 Дж/(моль ∙ К)

Энергию Гиббса при соответствующих температурах находим из соотношения

Так как ∆G₅₀₀>0, a ∆G₁₀₀₀<0, то восстановление Fе₂О₃ возможно при 1000 К и невозможно при 500 К.