Solve integrals with Wolfram|Alpha
More than just an online integral solver
Wolfram|Alpha is a great tool for calculating antiderivatives and definite integrals, double and triple integrals, and improper integrals. The Wolfram|Alpha Integral Calculator also shows plots, alternate forms and other relevant information to enhance your mathematical intuition.
Learn more about:
- Integrals »
Tips for entering queries
Use Math Input above or enter your integral calculator queries using plain English. To avoid ambiguous queries, make sure to use parentheses where necessary. Here are some examples illustrating how to ask for an integral using plain English.
- integrate x/(x-1)
- integrate x sin(x^2)
- integrate x sqrt(1-sqrt(x))
- integrate x/(x+1)^3 from 0 to infinity
- integrate 1/(cos(x)+2) from 0 to 2pi
- integrate x^2 sin y dx dy, x=0 to 1, y=0 to pi
- View more examples »
Access instant learning tools
Get immediate feedback and guidance with step-by-step solutions for integrals and Wolfram Problem Generator
Learn more about:
- Step-by-step solutions »
- Wolfram Problem Generator »
What are integrals?
Integration is an important tool in calculus that can give an antiderivative or represent area under a curve.
The indefinite integral of , denoted , is defined to be the antiderivative of . In other words, the derivative of is . Since the derivative of a constant is 0, indefinite integrals are defined only up to an arbitrary constant. For example,, since the derivative of is . The definite integral of from to , denoted , is defined to be the signed area between and the axis, from to .
Both types of integrals are tied together by the fundamental theorem of calculus. This states that if is continuous on and is its continuous indefinite integral, then . This means . Sometimes an approximation to a definite integral is desired. A common way to do so is to place thin rectangles under the curve and add the signed areas together. Wolfram|Alpha can solve a broad range of integrals
How Wolfram|Alpha calculates integrals
Wolfram|Alpha computes integrals differently than people. It calls Mathematica’s Integrate function, which represents a huge amount of mathematical and computational research. Integrate does not do integrals the way people do. Instead, it uses powerful, general algorithms that often involve very sophisticated math. There are a couple of approaches that it most commonly takes. One involves working out the general form for an integral, then differentiating this form and solving equations to match undetermined symbolic parameters. Even for quite simple integrands, the equations generated in this way can be highly complex and require Mathematica’s strong algebraic computation capabilities to solve. Another approach that Mathematica uses in working out integrals is to convert them to generalized hypergeometric functions, then use collections of relations about these highly general mathematical functions.
While these powerful algorithms give Wolfram|Alpha the ability to compute integrals very quickly and handle a wide array of special functions, understanding how a human would integrate is important too. As a result, Wolfram|Alpha also has algorithms to perform integrations step by step. These use completely different integration techniques that mimic the way humans would approach an integral. This includes integration by substitution, integration by parts, trigonometric substitution and integration by partial fractions.
Интегралы
Вычислим интеграл с использованием функции Integrate:
| In[1]:= |
|
| Out[1]= |
Или набрав ESCinttESC для создания заполняемого математического шаблона:
(Подробная информация о заполняемых шаблонах представлена в разделе Математическая нотация.)
| In[2]:= |
⨯ [Integral]8 x^4 [DifferentialD]x |
| Out[2]= |
Для задания определенного интеграла наберем ESCdinttESC и укажем нижний и верхний пределы интегрирования:
| In[1]:= |
⨯ !( *SubsuperscriptBox[([Integral]), (0), ([Pi])](Sin[ x] [DifferentialD]x)) |
| Out[1]= |
Используем функцию NIntegrate для получения численного решения:
| In[2]:= |
⨯ NIntegrate[x^3 Sin[x] + 2 Log[3 x]^2, {x, 0, Pi}]
|
| Out[2]= |
Справочная информация: Математический анализ »
Вычисление интегралов и их применение — самая популярная на сегодня тема в блоге ”Wolfram|Alpha по-русски”.
В блоге ”Wolfram|Alpha по-русски” на тему интегралов существует отдельный раздел, который называется Интегральное исчисление.
Кроме теоретических аспектов интегрального исчисления, то есть собственно вычисления интегралов, существуют еще и практические, прикладные аспекты применения интегралов. Например, это вычисление площади фигуры, приближеннное вычисление «неберущихся» интегралов и другие, которые отнесены в раздел Прикладная математика.
Далее приводится список основных публикаций блога ”Wolfram|Alpha по-русски” на тему интегралов и их применения. А также на связанную с этим тему решения дифференциальных уравнений из раздела Дифференциальные уравнения.
Вот те публикации, на которые я хочу обратить ваше особое внимание. Здесь они расположены не в хронологическом порядке, а так, как я рекомендую их прочитать. Каждая из них заслуживает вашего внимания, поскольку раскрывает определенный аспект применения Wolfram|Alpha, как инструмента интегрирования:
- Неопределенный интеграл в Wolfram|Alpha
- Определенный интеграл в Wolfram|Alpha
- Несобственные интегралы в Wolfram|Alpha
- Численное интегрирование в Wolfram|Alpha
- Калькулятор интегралов в Wolfram|Alpha
- Как найти площадь плоской фигуры в Wolfram|Alpha
- Как найти площадь фигуры ограниченной кривыми линиями
- Как найти длину дуги кривой линии в Wolfram|Alpha
- Двойной интеграл в Wolfram|Alpha
- Калькулятор двойных интегралов в Wolfram|Alpha
- Тройной интеграл в Wolfram|Alpha
- Решение обыкновенных дифференциальных уравнений в Wolfram|Alpha
Вопросам решения дифференциальных уравнений и их систем, а также прикладным вопросам применения дифференциальных уравнений, в частности, вопросам математического моделирования, о которых также идет речь в блоге ”Wolfram|Alpha по-русски” в разделе Математическое моделирование, со временем будет посвящен отдельный пост.
Как найти производную в вольфраме?
Проще всего найти обычную производную функции f(x) в Wolfram|Alpha можно с помощью запроса-префикса d/dx. Чтобы получить пошаговое решение с пояснениями каждого шага, достаточно нажать «Show steps». Конечно, навряд ли можно научиться дифференцировать функции, используя исключительно Wolfram|Alpha.
Как посчитать двойной интеграл в вольфраме?
Для вычисления определенных двойных интегралов нужно просто указать пределы интегрирования. В простейшем случае, вычисление двойного интеграла в Wolfram|Alpha выполняется по запросу следующего вида: integrate x^2y+xy^2-x+y+5 dxdy, x=0..1, y=-1..2.
Чему равно значение определенного интеграла?
Определённый интеграл равен произведению длины отрезка интегрирования на значение подынтегральной функции в некоторой точке внутри его, т. е.
Как найти предел в вольфраме?
Для вычисления пределов Wolfram|Alpha использует запрос limit или lim. Вот так Wolfram|Alpha вычисляет первый замечательный предел: limit sin(x)/x, x->0.
Как найти производную n го порядка?
Производная n—го порядка является производной (n-1) порядка: y n = y n − 1 ′ . (Сама функция иногда считается производной 0-го порядка.)
Чему равна производная от тангенса?
Производная от тангенса равна единице, деленной на косинус в квадрате.
Что означает знак DX Под интегралом?
Определение. Если функция F (x) является первообразной для f (x), то выражение F (x) + С называется неопределённым интегралом от функции f (x) и обозначается символом ∫ f (x) dx.
Что такое интеграл с переменным верхним пределом?
Определенный интеграл с переменным верхним пределом является одной из первообразных для непрерывной подынтегральной функции. Другими словами, для любой непрерывной функции существует первообразная.
Чему равен неопределенный интеграл от 0?
Неопределенный интеграл есть множество всех первообразных функций. Именно поэтому к нему +C дописывают после взятия. Интеграл нуля отсюда в первом случае равен 0+C, а во втором C+C = C.
Как записать бесконечность в вольфрам?
Найдем предел на бесконечности: (Наберите ESCinfESC для ввода символа ∞ .)
Как скачать Wolfram Mathematica?
На странице продукта Mathematica на вашем пользовательском портале User Portal нажмите на ссылку Windows в строке “Mathematica + Documentation” и столбце “Standard Download”. Это загрузит менеджер загрузок Wolfram для Windows как для основного продукта Mathematica, так и для документации продукта.
Как найти формулу производной?
Чтобы найти производную, надо выражение под знаком штриха разобрать на составляющие простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции.
Как найти производную второго порядка?
Производной второго порядка от функции y=f(x) называется производная от ее первой производной, то есть y″(x)=(y′(x))′. Производной n−го порядка (или n−й производной) называется производной от производной n−1−го порядка т.
Как найти частные производные функции?
Частные производные функции нескольких переменных – это частная производная функции z по аргументу у . Чтобы вычислить частную производную ФНП по одному из её аргументов, нужно все другие её аргументы считать постоянными и проводить дифференцирование по правилам дифференцирования функции одного аргумента.
Что такое TG A?
Тангенс острого угла в прямоугольном треугольнике – это отношение противолежащего катета к прилежащему.
Чему равен тангенс в?
ТАНГЕНС (Tg α) острого угла в прямоугольном треугольнике равняется отношение противолежащего катета к прилежащему катету.
Чему равна Производная от CTG?
Производная котангенса равна минус единица, деленная на синус в квадрате.
Как правильно вводить формулы на вольфрам альфа
Основные операции
- Сложение
: a+b
- Вычитание
: a-b
- Умножение
: a*b
- Деление
: a/b
- Возведение в степень
: a^b
- Примеры
- 314+278; 314—278; 314*278; 314^278;
- (a^2+b^2)+(a^2-b^2); (a^2+b^2)/(a^2-b^2); (a+b)^(2+2/3).
Знаки сравнения
- Меньше
: <
- Больше
: >
- Равно
: = или ==
- Меньше или равно
: <=
- Больше или равно
: >=
Логические символы
- И
: &&
- ИЛИ
: ||
- НЕ
: !
Основные константы
- Число
: Pi
- Число
: E
- Бесконечность
: Infinity или inf
Основные функции
: x^a
модуль x: abs(x)
Решение уравнений
Чтобы получить решение уравнения вида 
- Примеры
- Solve[Cos[x]+Cos[2x]+Sin[4x]=0,x] или Cos[x]+Cos[2x]+Sin[4x]=0;
- Solve[x^5+x^4+x+1=0,x] или x^5+x^4+x+1=0;
- Solve[Log[3,x^2+x+1]-Log[9,x^2]=0,x] или Log[3,x^2+x+1]-Log[9,x^2]=0.
Если Ваше уравнение содержит несколько переменных, то запись: f[x, y,…,z]=0 даст весьма разнообразный набор сведений, таких как решение в целых числах, частные производные функции 
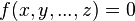

- Примеры
- Cos[x+y]=0 или Solve[Cos[x+y]=0,x] или Solve[Cos[x+y]=0,y];
- x^2+y^2-5=0 или Solve[x^2+y^2-5=0,x] или Solve[x^2+y^2-5=0,y];
- x+y+z+t+p+q=9.
Решение неравенств
Решение в Wolfram Alpha неравенств типа 
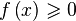

- Примеры
- Cos[10x]-1/2>0 или Solve[Cos[10x]-1/2>0,x];
- x^2+5x+10>=0 или Solve[x^2+5x+10>=0,x].
Если Ваше неравенство содержит несколько переменных, то запись: f[x, y,…,z]>0 или f[x, y,…,z]>=0 даст весьма разнообразный набор сведений, как и в случае соответствующих уравнений. Чтобы получить решение такого неравенства по какой-либо одной из переменных нужно написать в строке: Solve[f[x, y,…,z]>0,j] или Solve[f[x, y,…,z]>=0,j], где 
- Примеры
- Cos[x+y]>0 или Solve[Cos[x+y]>0,x] или Solve[Cos[x+y]>0,y];
- x^2+y^3-5<0 или Solve[x^2+y^3-5<0,x] или Solve[x^2+y^3-5<0,y];
- x+y+z+t+p+q>=9.
Решение различных систем уравнений, неравенств и уравнений
Решение систем различного вида в Wolfram Alpha крайне просто. Достаточно набрать уравнения и неравенства Вашей системы, точно так, как это описано выше в пунктах 7. и 8., соединяя их союзом «И», который в Wolfram Alpha имеет вид &&.
- Примеры
- x^3+y^3==9&&x+y=1;
- x+y+z+p==1&&x+y-2z+3p=2&&x+y-p=-3;
- Sin[x+y]+Cos[x+y]==Sqrt[3]/4&&x+y²=1;
- Log[x+5]=0&&x+y+z<1.
Построение графиков функций
Сервис Wolfram Alpha поддерживает возможность построения графиков функций как вида 


![x in left[ {a,b} right]](https://upload.wikimedia.org/math/7/4/2/742cbcce0d00d20060f55c3603104e64.png)

![y in left[ {c,d} right]](https://upload.wikimedia.org/math/5/3/0/530e43b31b783941629e7b4a8d2c8866.png)
- Примеры
- Plot[x^2+x+2, {x,-1,1}];
- Plot[x^2+x+2, {x,-1,1},{y,-1,5}];
- Plot[Sin[x]^x, {x,-Pi,E}];
- Plot[Sin[x]^x, {x,-Pi,E},{y,0,1}].
Если Вам требуется построить сразу несколько графиков на одном рисунке, то перечислите их, используя союз «И»:Plot[f[x]&&g[x]&&h[x]&&…&&t[x],{x, a, b}].
- Примеры
- Plot[x&&x^2&&x^3, {x,-1,1},{y,-1,1}];
- Plot[Sin[x]&&Sin[5x]&&Sin[10x]&&Sin[15x], {x,-5,5}].
Для того, чтобы построить график функции 
![x in left[ {a,b} right],y in left[ {c,d} right]](https://upload.wikimedia.org/math/8/2/b/82b905749a5dce2a347335bbfa1eb8f1.png)


- Примеры
- Plot[Sin[x^2+y^2],{x,-1,-0.5},{y,-2,2}];
- Plot[xy,{x,-4,4},{y,-4,4}].
Математический анализ
Wolfram Alpha способен находить пределы функций, последовательностей, различные производные, определенные и неопределенные интегралы, решать дифференциальные уравнения и их системы и многое многое другое.
Пределы
Для того, чтобы найти предел последовательности 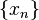
- Примеры
- Limit[n^3/(n^4 + 2*n), n -> Infinity];
- Limit[(1+1/n)^n, n -> Infinity].
Найти предел функции 

- Примеры
- Limit[Sin[x]/x, x -> 0];
- Limit[(1-x)/(1+x), x -> −1].
Производные
Для того, чтобы найти производную функции 



Важно подчеркнуть, что Wolfram Alpha выдает пошаговое нахождение производной при нажатии на «Show Steps» в правом верхнем углу выдаваемого ей ответа.
- Примеры
- D[x*E^x, x];
- D[x^3*E^x, {x,17}];
- D[x^3*y^2*Sin[x+y], x];
- D[x^3*y^2*Sin[x+y], y],
- D[x/(x+y^4), {x,6}].
Интегралы
Для того, чтобы найти неопределенный интеграл от функции 
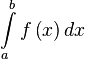
Важно подчеркнуть, что Wolfram Alpha выдает пошаговое нахождение интеграла при нажатии на «Show Steps» в правом верхнем углу выдаваемого ей ответа.
- Примеры
- Integrate[Sin[x]/x², x];
- Integrate[x^10*ArcSin[x], x];
- Integrate[(x+Sin[x])/x, {x,1,100}];
- Integrate[Log[x^3+1]/x^5, {x,1,Infinity}].
Дифференциальные уравнения и их системы
Чтобы найти общее решение дифференциального уравнения 
Если Вам требуется решить задачу Коши, то впишите: F[x, y, y’,y”,…], y[s]==A,y'[s]==B, …. Если нужно получить решение краевой задачи, что краевые условия, так же перечисляются через запятую, причем они должны иметь вид y[s]==S.
Решение систем дифференциальных уравнений также просто, достаточно вписать: {f_1,f_2,…,f_n}, где f_1, f_2, …, f_n — дифференциальные уравнения, входящие в систему. К сожалению, решение задач Коши и краевых задач для систем дифференциальных уравнений пока-что не поддерживается.
- Примеры
- y”’+y”+y=Sin[x];
- y”+y’+y=ArcSin[x];
- y”+y+y^2=0;
- y”=y, y[0]==0, y'[0]=4;
- y+x*y’=x, y[6]=2;
- y”'[x]+2y”[x]-3y'[x]+y=x, y[0]=1, y[1]=2, y'[1]=2;
- {x’+y’=2, x’-2y’=4}.
Ошибки при работе с системой
Система может допускать некоторые ошибки при решении сложных задач. К примеру, если попытаться решить неравенство 
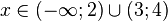
Разложение на множители
Например, разложить на множители
x2/3 – 3x + 12
Запишем как
factor x^2/3 – 3x + 12
и нажимаем равно (=).
Например, разложить на слагаемые
Запишем как
Partial fraction expansion(1-x^2)/(x^3+x)
используются формулы разложения функций в ряд Тейлора (Taylor series) и ряд Маклорена (Maclaurin series) или
Series expansion at x=0
Разложить в ряд Лорана:
Laurent expansion z*cos(1/z) at z =0
Чтобы упростить выражение f[x], наберите команду Simplify[f[x]]
Комплексно сопряженное z*
Египетская дробь:
Egyptian fraction expansion:
11/30=1/3+1/30
parametric plot (3*cos t, sin t, 2t), t=0..2pi
interpolation polynomial {1,4,9,16}
Транспонировать матрицу: transpose {{8,2,-3,2},{-6,3,-2,1},{3,8,4,-8},{2,1,-6,2}}
Обратная матрица inverse {{a, b}, {c, d}}
Собственные числа (вектора) матрицы: eigenvalues( ( transpose{{1,0,0,0},{0,1,0,0},{0,0,1,0},{0,0,0,1}})-1/67.42598*({{8,2,-3,2},{-6,3,-2,1},{3,8,4,-8},{2,1,-6,2}}*{{8,2,-3,2},{-6,3,-2,1},{3,8,4,-8},{2,1,-6,2}}))
Решение СЛАУ : {{8,2,-3,2},{-6,3,-2,1},{3,8,4,-8},{2,1,-6,2}}*{{x_1},{x_2},{x_3},{x_4}}={{102},{-47},{-122},{-24}}
{{-9,5,2},{5,-6,3},{4,1,-5}}*{{x},{y},{z}}={{0},{0},{0}}
Интегральное преобразование Лапласа —- LT
Обратное преобразование Лапласа — ILT
 : a+b
: a+b : a-b
: a-b : a*b
: a*b : a/b
: a/b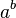 : a^b
: a^b : <
: <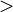 : >
: > : = или ==
: = или == : <=
: <=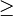 : >=
: >= : &&
: && : ||
: || : !
: ! : Pi
: Pi : E
: E : Infinity или inf
: Infinity или inf
 : x^a
: x^a