Вращающий момент как найти направление

Вращение является типичным видом механического движения, которое часто встречается в природе и технике. Любое вращение возникает в результате воздействия некоторой внешней силы на рассматриваемую систему. Эта сила создает так называемый вращающий момент. Что он собой представляет, от чего зависит, рассматривается в статье.

Процесс вращения

Прежде чем рассматривать концепцию вращающего момента, дадим характеристику систем, к которым может быть применена эта концепция. Система вращения предполагает наличие в ней оси, вокруг которой осуществляется круговое движение или поворот. Расстояние от этой оси до материальных точек системы называется радиусом вращения.

С точки зрения кинематики, процесс характеризуется тремя угловыми величинами:

• углом поворота θ (измеряется в радианах);
• угловой скоростью ω (измеряется в радианах в секунду);
• ускорением угловым α (измеряется в радианах в секунду квадратную).

Эти величины связаны друг с другом следующими равенствами:

ω = dθ/dt;

α = dω/dt.

Примерами вращения в природе являются движения планет по своим орбитам и вокруг своих осей, движения смерчей. В быту и технике рассматриваемое движение характерно для моторов двигателей, гаечных ключей, строительных кранов, открывания дверей и так далее.

Определение момента силы

Теперь перейдем к непосредственной теме статьи. Согласно физическому определению, момент силы представляет собой векторное произведение вектора приложения силы относительно оси вращения на вектор самой силы. Соответствующее математическое выражение можно записать так:

M¯ = [r¯*F¯].

Здесь вектор r¯ направлен от оси вращения к точке приложения силы F¯.

В этой формуле вращающего момента M¯ сила F¯ может быть направлена как угодно относительно направления оси. Тем не менее параллельная оси компонента силы не будет создавать вращения, если ось жестко закреплена. В большинстве задач по физике приходится рассматривать силы F¯, которые лежат в плоскостях перпендикулярных оси вращения. В этих случаях абсолютное значение вращающего момента можно определить по следующей формуле:

|M¯| = |r¯|*|F¯|*sin(β).

Где β является углом между векторами r¯ и F¯.

Что такое рычаг силы?

Рычаг силы играет важную роль при определении величины момента силы. Чтобы понять, о чем идет речь, рассмотрим следующий рисунок.

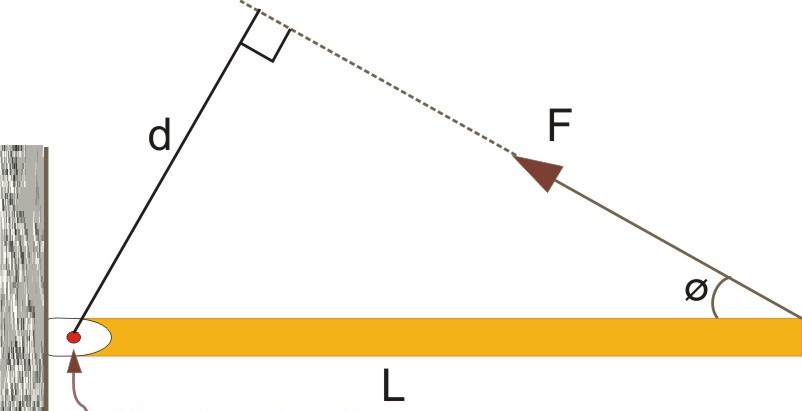
Здесь показан некоторый стержень длиною L, который закреплен в точке вращения одним из своих концов. На другой конец действует сила F, направленная под острым углом φ. Согласно определению момента силы, можно записать:

M = F*L*sin(180^o-φ).

Угол (180^o-φ) появился потому, что вектор L¯ направлен от закрепленного конца к свободному. Учитывая периодичность тригонометрической функции синуса, можно переписать это равенство в таком виде:

M = F*L*sin(φ).

Теперь обратим внимание на прямоугольный треугольник, построенный на сторонах L, d и F. По определению функции синуса, произведение гипотенузы L на синус угла φ дает значение катета d. Тогда приходим к равенству:

M = F*d.

Линейная величина d называется рычагом силы. Он равен расстоянию от вектора силы F¯ до оси вращения. Как видно из формулы, понятием рычага силы удобно пользоваться при вычислении момента M. Полученная формула говорит о том, что вращающий момент максимальный для некоторой силы F будет возникать только тогда, когда длина радиус-вектора r¯ (L¯ на рисунке выше) будет равна рычагу силы, то есть r¯ и F¯ будут взаимно перпендикулярны.

Направление действия величины M¯

Выше было показано, что вращающий момент – это векторная характеристика для данной системы. Куда направлен этот вектор? Ответить на этот вопрос не представляет особого труда, если вспомнить, что результатом произведения двух векторов является третий вектор, который лежит на оси, перпендикулярной плоскости расположения исходных векторов.

Остается решить, будет ли направлен момент силы вверх или вниз (на читателя или от него) относительно упомянутой плоскости. Определить это можно или по правилу буравчика, или с помощью правила правой руки. Приведем оба правила:

• Правило правой руки. Если расположить правую кисть таким образом, чтобы четыре ее пальца двигались от начала вектора r¯ к его концу, а затем от начала вектора F¯ к его концу, то большой палец, оттопыренный, укажет на направление момента M¯.
• Правило буравчика. Если направление вращения воображаемого буравчика совпадает с направлением вращательного движения системы, то поступательное движение буравчика укажет на направление вектора M¯. Напомним, что он вращается только по часовой стрелке.

Оба правила являются равноправными, поэтому каждый может использовать то, которое является для него более удобным.

При решении практических задач разное направление вращающего момента (вверх – вниз, влево – вправо) учитывается с помощью знаков “+” или “-“. Следует запомнить, что за положительное направление момента M¯ принято считать такое, которое приводит к вращению системы против часовой стрелки. Соответственно, если некоторая сила приводит к вращению системы по ходу стрелки часов, то создаваемый ее момент будет иметь отрицательную величину.

Физический смысл величины M¯

В физике и механике вращения величина M¯ определяет способность силы или суммы сил совершать вращение. Поскольку в математическом определении величины M¯ стоит не только сила, но и радиус-вектор ее приложения, то именно последний во многом определяет отмеченную вращательную способность. Чтобы понятнее было, о какой способности идет речь, приведем несколько примеров:

• Каждый человек, хотя бы один раз в жизни пытался открыть дверь, взявшись не за ручку, а толкнув ее недалеко от петель. В последнем случае приходится прилагать значительное усилие, чтобы добиться желаемого результата.
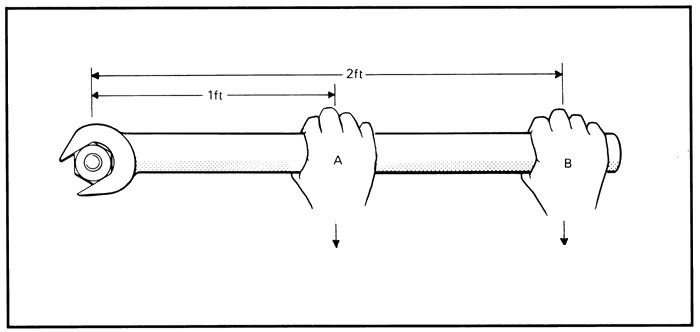
• Чтобы открутить гайку с болта, используют специальные гаечные ключи. Чем длиннее ключ, тем легче открутить гайку.
• Чтобы ощутить важность рычага силы, предлагаем читателям проделать следующий эксперимент: взять стул и попытаться удержать его одной рукой на весу, в одном случае руку прислонить к телу, в другом – выполнить задачу на прямой руке. Последнее для многих окажется непосильной задачей, хотя вес стула остался тем же самым.

Единицы измерения момента силы

Несколько слов также следует сказать о том, в каких единицах в СИ измеряется вращающий момент. Согласно записанной для него формуле, он измеряется в ньютонах на метр (Н*м). Однако в этих единицах также измеряется работа и энергия в физике (1 Н*м = 1 джоуль). Джоуль для момента M¯ не применяется, поскольку работа является скалярной величиной, M¯ же – это вектор.

Тем не менее совпадение единиц момента силы с единицами энергии не является случайным. Работа по вращению системы, совершенная моментом M, рассчитывается по формуле:

A = M*θ.

Откуда получаем, что M также может быть выражен в джоулях на радиан (Дж/рад).

Динамика вращения

В начале статьи мы записали кинематические характеристики, которые используются для описания движения вращения. В динамике вращения главным уравнением, которое использует эти характеристики, является следующее:

M = I*α.

Действие момента M на систему, имеющую момент инерции I, приводит к появлению углового ускорения α.

Данную формулу применяют, для определения угловых частот вращения в технике. Например, зная вращающий момент асинхронного двигателя, который зависит от частоты тока в катушке статора и от величины изменяющегося магнитного поля, а также зная инерционные свойства вращающегося ротора, можно определить, до какой скорости вращения ω раскручивается ротор двигателя за известное время t.

Пример решения задачи

Невесомый рычаг, длина которого составляет 2 метра, посередине имеет опору. Какой вес следует положить на один конец рычага, чтобы он находился в состоянии равновесия, если с другой стороны опоры на расстоянии 0,5 метра от нее лежит груз массой 10 кг?

Очевидно, что равновесие рычага наступит, если моменты сил, создаваемые грузами, будут равны по модулю. Сила, создающая момент в данной задаче, представляет собой вес тела. Рычаги силы равны расстояниям от грузов до опоры. Запишем соответствующее равенство:

M₁ = M₂ =>

m₁*g*d₁ = m₂*g*d₂ =>

P₂ = m₂*g = m₁*g*d₁/d₂.

Вес P₂ получим, если подставим из условия задачи значения m₁ = 10 кг, d₁ = 0,5 м, d₂ = 1 м. Записанное равенство дает ответ: P₂ = 49,05 ньютона.

Для
описания динамики вращательного движения
твердого тела необходимо ввести понятие
момента силы.
Момент силы
относительно некоторой точки — это
векторное произведение силы
на кратчайшее
расстояние
от этой точки до линии действия силы.
Момент силы
— аксиальный
вектор. Он
направлен вдоль оси вращения. Направление
вектора момента силы определяется
правилом буравчика, а величина его равна
M.
При этом надо различать понятия момента
силы относительно
точки и относительно оси. Если сила f
приложена к материальной точке А, то
моментом силы М относительно произвольной
точки О называется векторное произведение
радиуса-вектора r, проведенного из точки
О к точке А, и вектора силы:  М = [ r f ]
.  Модуль векторного произведения
 = r f sin a, а  направление вектора М
определяется правилом правого буравчика:
направление первого вектора r по
кратчайшему пути вращается к направлению
второго вектора f, а движение оси буравчика
при этом вращении показывает направление
вектора М. Моментом силы относительно
произвольной оси z называется векторное
произведение радиуса-вектора r и
составляющей f  силы f , приложенной
в точке А:  М = [ r  f  ] где составляющая
f   представляет собой проекцию
силы f на плоскость, перпендикулярную
оси z  и проходящую через точку А , а
r – радиус- вектор точки А, лежащий в этой
плоскости. M=Fd, т. е. момент силы равен
произведению силы F на длину перпендикуляра
d, опущенного из оси на направление силы.
Длину перпендикуляра, опущенного из
оси на направление силы, называют плечом
силы. Значит, момент силы равен произведению
величины силы на плечо силы. Ясно, что
перенесение точки приложения силы вдоль
ее направления не меняет ее момента
(рис. 120). Если направление силы проходит
через ось вращения, то плечо силы равно
нулю; следовательно, равен нулю и момент
силы этом случае сила не вызывает
вращения тела: сила, момент которой
относительно данной оси равен нулю, не
вызывает вращения вокруг этой оси.
Пользуясь понятием момента силы, мы
можем по-новому сформулировать условия
равновесия тела, закрепленного на оси
и находящегося под действием двух сил.
Как мы видели, для равновесия необходимо,
чтобы силы стремились вращать тело в
противоположных направлениях и чтобы
произведения сил на их расстояния до
оси были равны. Значит, при равновесии
моменты обеих сил должны быть равны по
величине и противоположны по знаку.
Таким образом, для равновесия тела,
закрепленного на оси, алгебраическая
сумма моментов действующих на него сил
должна быть равна нулю. Так как момент
силы определяется произведением величины
силы на плечо, то единицу момента мы
получим, взяв силу, равную единице, плечо
которой также равно единице. Значит, в
системе СИ единицей момента силы является
момент силы в 1 н, действующей на плече
в 1 м, т. е. 1 н*м, в системе СГС —1 дин*см,
в системе МКСС— 1 кГ*м. Пользуясь данными
§ 45, найдем соотношения между этими
единицами:1 дин*см = 10^-7
н*м;   1 кГ*м = 9,8 н*м.

42. Как определить направление угловой скорости?

Углова́я
ско́рость —
векторная
физическая величина, характеризующая
скорость вращения тела. Вектор угловой
скорости по величине равен углу
поворота тела в единицу времени:

,

а
направлен по оси
вращения
согласно правилу
буравчика,
то есть, в ту сторону, в которую ввинчивался
бы буравчик
с правой резьбой, если бы вращался в ту
же сторону. Единица
измерения
угловой скорости, принятая в системах
СИ
и СГС) —
радианы
в секунду.
(Примечание: радиан,
как и любые единицы измерения угла, —
физически безразмерен, поэтому физическая
размерность угловой скорости —
просто [1/секунда]).Определим угловую
скорость как вектор, величина которого
численно равна угловой скорости, b
направленный вдоль оси вращения, причем,
если смотреть с конца этого вектора, то
вращение направлено против часовой
стрелки.
Исторически сложилось, что положительным
направлением вращения считается вращение
«против часовой стрелки», хотя, конечно,
выбор этого направления абсолютно
условен. Для определения направления
вектора угловой скорости можно также
воспользоваться «правилом буравчика»
(которое также называется «правилом
правого винта») – если направление
движения ручки буравчика (или штопора)
совместить с направлением вращения, то
направление движения всего буравчика
совпадет с направлением вектора угловой
скорости.

43.
Как
определить направление углового
ускарения? Угловое
ускорение
– векторная физическая величина,
характеризующая быстроту изменения
угловой скорости твёрдого тела.Угловое
ускорение
равно первой производной от угловой
скорости по времени.Формула угловой
скорости:

Единица
углового ускорения – радиан в секунду
в квадрате.

Углово́е
ускоре́ние —
псевдовекторная
физическая
величина,
характеризующая быстроту изменения
угловой
скорости
твёрдого
тела.

При
вращении
тела вокруг неподвижной оси,
угловое ускорение по модулю равно^[1]:

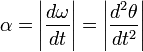
Вектор
углового ускорения α
направлен вдоль оси вращения (в сторону

при
ускоренном вращении и противоположно

 —
при замедленном).

При
вращении вокруг неподвижной точки
вектор углового ускорения определяется
как первая производная от вектора
угловой скорости ω
по времени^[2],
то есть

,

и
направлен по касательной к годографу
вектора
в
соответствующей его точке.

44.
При
каком условии мы имеем право считать в
лабораторной работе №4 «Изучение
основного закона динамики вращательного
движения» линейное ускорение точек на
ободе щкива равным ускорению поступательного
движения груза?

Момент
сил создается грузом m, привязанным к
нити Н, ко­торая навита на один из
шкивов. Если момент сил трения M_тр,
при­ложенный к оси маятника, мал по
сравнению с моментом силы натяжения
нити, то проверка уравнения

не представляет труда. Действи­тельно,
измеряя время t,
в течение которого груз из состояния
покоя опустится на расстояние h,
можно легко найти ускорение груза а,
в проекции на координатную ось,
совпадающую с направлением движения:

, которое
связано с угловым ускорением 
(при отсутствии проскальзывания нити
относительно обода шкива) очевидным
соотношением

, где
r
– радиус шкива.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

В этой главе…

• Переходим от поступательного движения к вращательному движению
• Вычисляем тангенциальную скорость и тангенциальное ускорение
• Выясняем связь между угловым ускорением и угловой скоростью
• Разбираемся с моментом силы
• Поддерживаем вращательное движение

Эта и следующая главы посвящены вращательному движению объектов самой разной природы: от космических станций до пращи. Именно такое движение стало причиной того, что наша планета имеет круглую форму. Если вам известны основные свойства прямолинейного движения и законы Ньютона (они подробно описываются в двух первых частях этой книги), то вы сможете быстро овладеть основами вращательного движения. Даже если вы позабыли некоторые сведения из прежних глав, не беда, ведь к ним всегда можно вернуться в случае необходимости. В этой главе представлены основные понятия вращательного движения: угловая скорость угловое ускорение, тангенциальное ускорение, момент силы и т.п. Однако довольно слов, приступим к делу!

Переходим от прямолинейного движения  к вращательному

Для такого перехода нужно изменить уравнения, которые использовались ранее для описания прямолинейного движения. В главе 7 уже упоминались некоторые эквиваленты (или аналоги) из мира прямолинейного и вращательного движения.

Вот как выглядят основные формулы прямолинейного движения, которые подробно описываются в главе 3:

• ​( v=Delta{s}/Delta{t} )​, где ​( v )​ — это скорость, ​( Delta{s} )​ — перемещение, a ( Delta{t} ) — время перемещения;
• ( a=Delta{v}/Delta{t} ), где ( a ) — это ускорение, ( Delta{v} ) — изменение скорости, a ( Delta{t} ) — время изменения скорости;
• ​( Delta{s}=v_0(t_1-t_0)+{}^1!/!_2a(t_1-t_0)^2 )​, где ​( v_0 )​ — это начальная скорость, ​( t_0 )​ — это начальный момент времени, a ​( t_1 )​ — это конечный момент времени;
• ​( v^2_1-v^2_0=2aDelta{s} )​, где ​( v_1 )​ — это конечная скорость.

По аналогии можно легко вывести основные формулы вращательного движения:

• ​( omega=Delta{theta}/Delta{t} )​, где ​( omega )​ — угловая скорость, ​( Delta{theta} )​ — угол поворота, ( Delta{t} ) — время поворота на угол ( Delta{theta} );
• ​( alpha=Delta{omega}/Delta{t} )​, где ​( alpha )​ — угловое ускорение, ​( Delta{omega} )​ — изменение угловой скорости, ​( Delta{t} )​ — время изменения угловой скорости;
• ​( theta=omega_0(t_1-t_0)+{}^1!/!_2a(t_1-t_0)^2 )​, где ​( omega_0 )​ — это начальная скорость;
• ​( omega^2_1-w^2_0=2as )​, где ​( omega_1 )​ — это конечная скорость.

Разбираемся с параметрами вращательного движения

В физике движение принято разделять на поступательное и вращательное. При поступательном движении любая прямая, связанная с движущимся объектом, остается параллельной самой себе. При вращательном движении все точки тела движутся по окружностям. Тангенциальным движением называется часть вращательного движения, происходящего по касательной к окружности вращения, а радиальным (или нормальным) движением — часть вращательного движения, происходящего перпендикулярно (по нормали) к касательной, т.е. вдоль радиуса окружности.

Параметры прямолинейного поступательного и вращательного движений можно связать следующими формулами:

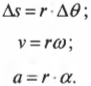
Допустим, колеса мотоцикла вращаются с угловой скоростью ​( omega )​, равной 21,5( 21,5pi )​ радиан в секунду. С какой скоростью едет мотоцикл? Чтобы дать ответ на этот вопрос, достаточно воспользоваться простой формулой связи линейной и угловой скорости.

Вычисляем линейную скорость вращательного движения

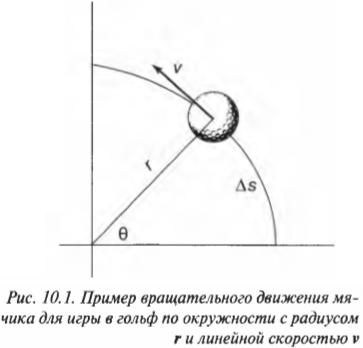
Скорость тангенциального движения материальной точки принято называть линейной скоростью вращательного движения. На рис. 10.1 приведен пример вращения мячика для игры в гольф по окружности с радиусом ​( mathbf{r} )​ и линейной скоростью ( mathbf{v} ). Скорость ( mathbf{v} ) является векторной величиной, т.е. обладает величиной и направлением (подробнее о векторах рассказывается в главе 4), перпендикулярным радиус-вектору ( mathbf{r} ).

Угловая скорость связана с линейной скоростью соотношением ​( v=romega )​, которое легко интуитивно понять. При одинаковой угловой скорости, чем дальше материальная точка от центра окружности вращения, тем больше ее линейная скорость.

Попробуем получить уже упомянутую выше формулу связи линейной и угловой скорости ( v=romega ). Длина окружности ​( L )​ радиуса ​( r )​ выражается известной формулой ​( L=2pi r )​, а полный угол, который охватывает окружность, равен ​( 2pi )​ радиан. Соответственно, длина дуги окружности длиной ​( Delta s )​, охватывающая угол ​( Deltatheta )​, равна:

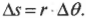
Из формулы прямолинейного движения

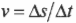
путем подстановки выражения для ​( Delta s )​ получим:

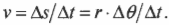
Поскольку:

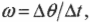
где ​( omega )​ — угловая скорость, ​( Delta{theta} )​— угол поворота, ​( Delta{t} )​ — время поворота на угол ( Delta{theta} ), то:

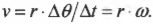
Теперь можно легко и просто дать ответ на вопрос, поставленный в конце предыдущего раздела, т.е. определить скорость мотоцикла по угловой скорости вращения его колес. Итак, колеса мотоцикла вращаются с угловой скоростью ( omega ), равной 21,5​( pi ) радиан в секунду. Пусть радиус колеса ​( r )​ равен 40 см, тогда достаточно использовать следующую формулу:

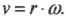
Подставляя в нее значения, получим:

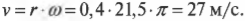
Итак, скорость мотоцикла равна 27 м/с или 97 км/ч.

Вычисляем тангенциальное ускорение

Тангенциальным ускорением называется скорость изменения величины линейной скорости вращательного движения. Эта характеристика вращательного движения очень похожа на линейное ускорение прямолинейного движения (см. главу 3). Например, точки на колесе мотоцикла в момент старта имеют нулевую линейную скорость, а спустя некоторое время после разгона ускоряются до некоторой ненулевой линейной скорости. Как определить это тангенциальное ускорение точки колеса? Переформулируем вопрос: как связать линейное ускорение

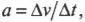
где ​( a )​ — это ускорение, ​( Delta v )​ — изменение скорости, a ​( Delta t )​ — время изменения скорости, с угловым ускорением

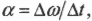
где ( Deltaomega ) — изменение угловой скорости, ( Delta t ) — время изменения угловой скорости?

Как мы уже знаем, линейная и угловая скорости связаны равенством

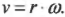
Подставим это выражение в предыдущую формулу линейного ускорения:

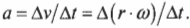
Поскольку радиус остается постоянным, то его можно вынести за скобки:

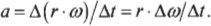
Поскольку угловое ускорение ​( alpha=Deltaomega/Delta t )​, то:

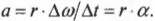
Итак, получаем следующую формулу связи между линейным и угловым ускорением:

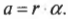
Иначе говоря, тангенциальное ускорение равно произведению радиуса на угловое ускорение.

Вычисляем центростремительное ускорение

Центростремительнным ускорением называется ускорение, необходимое для удержания объекта на круговой орбите вращательного движения. Как связаны угловая скорость и центростремительное ускорение? Формула для центростремительного ускорения уже приводилась ранее (см. главу 7):

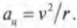
Теперь, используя известную формулу связи линейной и угловой скорости ​( v=romega )​, получим:

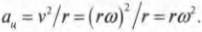
По этой формуле можно определить величину центростремительного ускорения по известной угловой скорости и радиусу. Например, для вычисления центростремительного ускорения Луны, вращающейся вокруг Земли, удобно использовать именно эту формулу.

Луна делает полный оборот вокруг Земли за 28 дней, т.е. за 28 дней Луна проходит ​( 2pi )​ радиан. Отсюда получаем угловую скорость Луны:

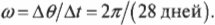
Чтобы получить значение угловой скорости в привычных единицах, следует преобразовать дни в секунды:

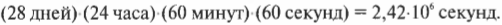
После подстановки этого значения в предыдущую формулу получим:

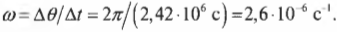
Средний радиус орбиты Луны равен 3,85·10⁸ м. Подставляя эти значения угловой скорости и радиуса в формулу центростремительного ускорения, получим:

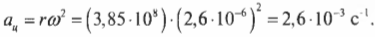
Зная это ускорение и массу Луны, которая равна 7,35·10²² кг, можно определить центростремительную силу, необходимую для удержания Луны на ее орбите:

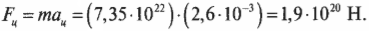
Используем векторы для изучения вращательного движения

В предыдущих разделах этой главы угловая скорость и угловое ускорение рассматривались как скаляры, т.е. как параметры, характеризующиеся только величиной. Однако эти параметры вращательного движения, на самом деле, являются векторами, т.е. они обладают величиной и направлением (см. главу 4). В этом разделе рассматривается величина и направление некоторых параметров вращательного движения.

Определяем направление угловой скорости

Как нам уже известно, вращающееся колесо мотоцикла имеет не только угловую скорость, но и угловое ускорение. Что можно сказать о направлении вектора угловой скорости? Оно не совпадает с направлением линейной тангенциальной скорости, а… перпендикулярно плоскости колеса!

Эта новость всегда приводит к некоторому замешательству среди новичков: угловая скорость ​( omega )​, оказывается, направлена вдоль оси вращающегося колеса (рис. 10.2). Во вращающемся колесе единственной неподвижной точкой является его центр. Поэтому начало вектора угловой скорости принято располагать в центре окружности вращения.

Для определения направления вектора угловой скорости ( omega ) часто используют правило правой руки. Если охватить ладонью ось вращения, а пальцы свернуть так, чтобы они указывали на направление тангенциальной скорости, то вытянутый большой палец укажет направление вектора угловой скорости ( omega ).

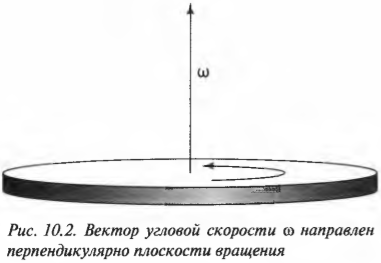
Теперь угловую скорость можно использовать так же, как и остальные векторные характеристики движения. Направление вектора угловой скорости можно найти по правилу правой руки, а величину — по приведенной ранее формуле. То, что вектор угловой скорости направлен перпендикулярно плоскости вращательного движения, часто вызывает некоторые трудности у начинающих, но к этому можно быстро привыкнуть.

Определяем направление углового ускорения

Если вектор угловой скорости направлен перпендикулярно плоскости вращательного движения, то куда направлен вектор углового ускорения в случае замедления или ускорения вращения объекта? Как известно (см. предыдущие разделы), угловое ускорение определяется формулой:

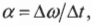
где ​( alpha )​ — угловое ускорение, ​( Deltaomega )​ — изменение угловой скорости, ​( Delta t )​— время изменения угловой скорости.

В векторной форме оно имеет следующий вид:

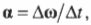
где ​( mathbf{alpha} )​ — вектор углового ускорения, а ​( Deltamathbf{omega} )​ — изменение вектора угловой скорости. Отсюда ясно, что направление вектора углового ускорения совпадает с направлением изменения вектора угловой скорости.

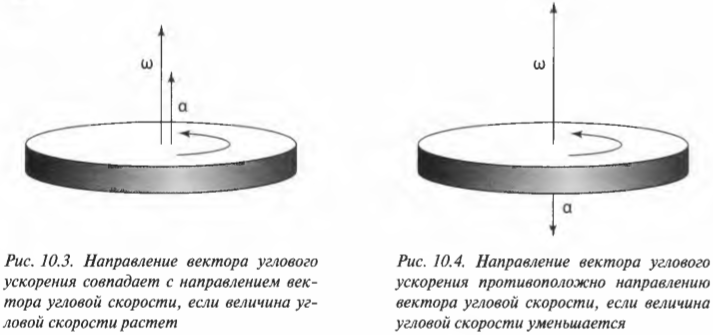
Если вектор угловой скорости меняется только по величине, то направление вектора углового ускорения параллельно направлению вектора угловой скорости. Если величина угловой скорости растет, то направление вектора углового ускорения совпадает с направлением вектора угловой скорости, как показано на рис. 10.3.

А если величина угловой скорости падает, то направление вектора углового ускорения противоположно направлению вектора угловой скорости, как показано на рис. 10.4.

Поднимаем грузы: момент силы

В физике большое значение имеет не только время, но и место приложения силы. Всем когда-либо приходилось пользоваться рычагом для перемещения тяжелых грузов. Чем длиннее рычаг, тем легче сдвинуть груз. На языке физики применение силы с помощью рычага характеризуется понятием момент силы.

Приложение момента силы неразрывно связано с вращательным движением объектов. Если приложить силу к краю карусели, то карусель начнет вращательное движение. Чем дальше точка приложения силы, тем легче раскрутить карусель до заданной угловой скорости (параметры вращательного движения описываются в главе 1 1 ).

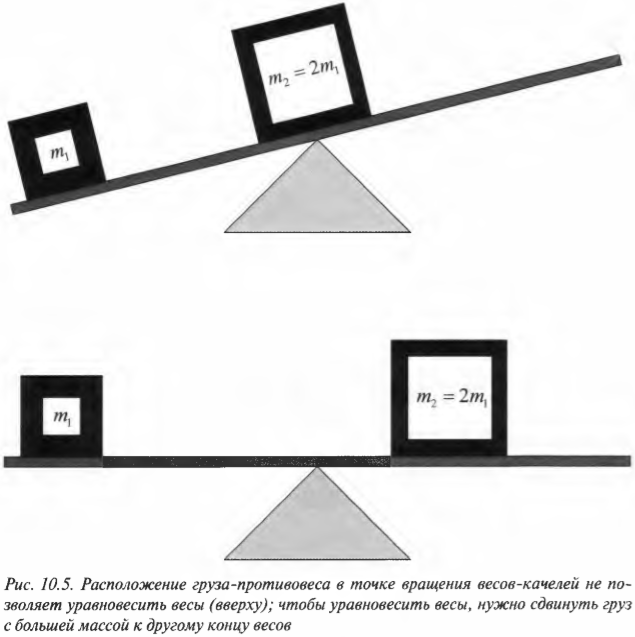
В верхней части рис. 10.5 показаны весы-качели с грузом массы ​( m_1 )​ на одном конце и грузом большей массы ​( m_2=2m_1 )​ посередине. Чтобы уравновесить весы-качели, нужно сместить груз с большей массой ​( m_2 )​ к другому концу весов, как показано в нижней части рис. 10.5. Как известно из опыта, размещение груза в точке вращения весов не приводит к уравновешиванию весов. Чтобы уравновесить весы, нужно сдвинуть груз с большей массой ( m_2=2m_1 ) к другому концу весов на расстояние вдвое меньшее, чем расстояние от точки вращения до второго груза с массой ​( m_1 )​.

Знакомимся с формулой момента силы

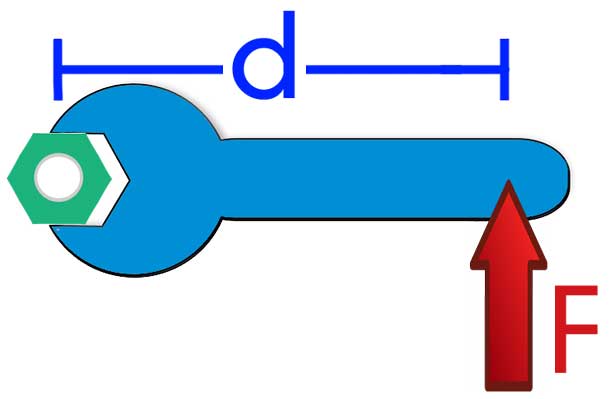
Для уравновешивания весов важно не только, какая сила используется, но и где она прикладывается. Расстояние от точки приложения силы до точки вращения называется плечом силы.

Предположим, что нам нужно открыть дверь, схематически показанную на рис. 10.6. Как известно из опыта, дверь практически невозможно открыть, если прилагать силу вблизи петель (см. схему А на рис. 10.6). Однако, если приложить силу посередине двери, то открыть ее будет гораздо проще (см. схему Б на рис. 10.6). Наконец, прилагая силу у противоположного края двери по отношению к расположению петель, ее можно открыть с еще меньшим усилием (см. схему В на рис. 10.6).

На рис. 10.6 расстояние от мест расположения петель до точки приложения силы и есть плечо силы. Моментом силы называется произведение прилагаемой силы ​( F )​ на плечо силы ​( l )​:

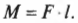
Момент силы в системе СИ измеряется в Н·м, а в системе СГС — в дин·см (подробнее эти системы единиц измерения описываются в главе 2).

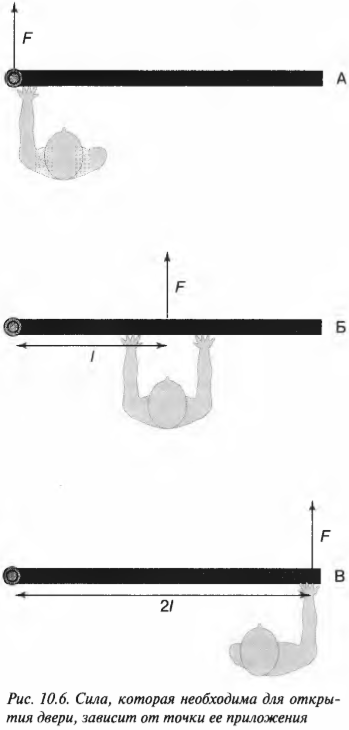
Вернемся к примеру на рис. 10.6, где требуется открыть дверь шириной 1 м с помощью силы величиной 200 Н. В случае А (см. рис. 10.6) плечо силы равно нулю и произведение этого плеча на силу любой величины (включая и силу 200 Н) даст нулевой момент силы. В случае Б (см. рис. 10.6) плечо силы равно половине ширины двери, т.е. плечо силы ​( l )​ равно 0,5 м и момент силы будет равен:

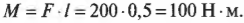
В случае В (см. рис. 10.6) плечо силы равно ширине двери, т.е. плечо силы ( l ) равно 1 м и момент силы будет равен:

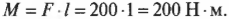
Итак, увеличение вдвое длины плеча при той же силе дает нам такое же увеличение момента силы. До сих пор сила прилагалась перпендикулярно к линии, соединяющей точку приложения силы и точку вращения. А что будет с моментом силы, если дверь будет немного приоткрыта и направление силы уже будет не перпендикулярным?

Разбираемся с направлением приложенной силы и плечом силы

Допустим, что сила приложена не перпендикулярно к поверхности двери, а параллельно, как показано на схеме А на рис. 10.7. Как известно из опыта, таким образом дверь открыть невозможно. Дело в том, что у такой силы нет проекции, которая бы могла вызвать вращательное движение. Точнее говоря, у такой силы нет ненулевого плеча для создания вращательного момента силы.

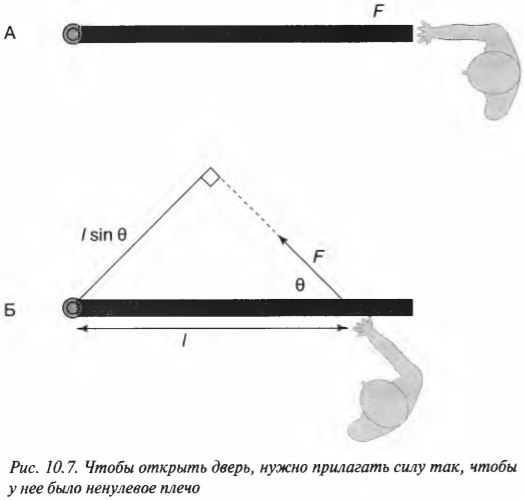
Размышляем над тем, как создается момент силы

Момент силы из предыдущего примера требуется создавать всегда для открытия двери независимо от того, какую дверь приходится открывать: легкую калитку изгороди или массивную дверь банковского сейфа. Как вычислить необходимый момент силы? Сначала нужно определить плечо сил, а потом умножить его на величину силы.

Однако не всегда все так просто. Посмотрите на схему Б на рис. 10.7. Как видите, сила прилагается под некоторым углом ​( theta )​. Как в таком случае определить плечо силы? Если бы угол ( theta ) был прямым, то мы могли бы воспользоваться уже известно нам формулой:

Однако в данном случае угол ( theta ) не является прямым.

В таком случае нужно просто помнить следующее правило: плечом силы называется длина перпендикуляра, опущенного из предполагаемой точки вращения на прямую, относительно которой действует сила.

Попробуем применить это правило определения плеча силы для схемы Б на рис. 10.7. Нужно продлить линию, вдоль которой действует сила, а потом опустить на нее перпендикуляр из точки вращения двери. Из полученного прямоугольного треугольника легко определить искомое плечо силы:

Если угол ( theta ) равен нулю, то никакого момента силы не возникает (см. схему А на рис. 10.7).

Итак, получаем для момента силы для схемы Б на рис. 10.7:

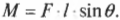
Например, если требуется открыть дверь шириной 1 м с помощью силы величиной 200 Н, приложенной под углом ( theta ) = 45°, то создаваемый момент этой силы будет равен:

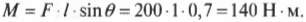
Как видите, этот момент силы 140 Н·м меньше, чем момент силы 200 Н·м, созданный под прямым углом на схеме В на рис. 10.6.

Определяем направление момента силы

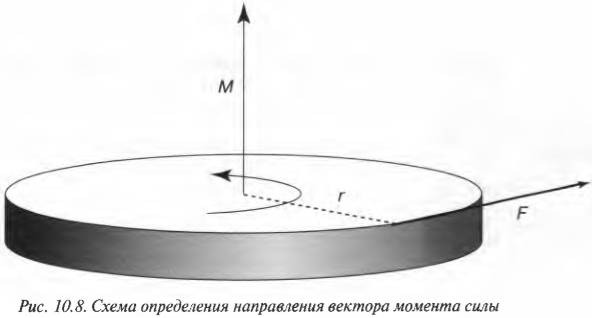
Учитывая все приведенные выше сведения о моменте силы, у читателя вполне может возникнуть подозрение, что момент силы обладает направлением. И это действительно так. Момент силы является векторной величиной, направление которой определяется по правилу правой руки. Если охватить ладонью ось вращения, а пальцы свернуть так, чтобы они указывали на направление силы, то вытянутый большой палец укажет направление вектора момента силы.

На рис. 10.8 показан пример силы ​( mathbf{F} )​ с плечом ( mathbf{l} ) и соответствующего вектора момента сил ( mathbf{M} ).

Уравновешиваем моменты сил

В жизни нам часто приходится сталкиваться с равновесными состояниями. Как равновесное механическое состояние определяется с точки зрения физики? Обычно физики подразумевают под равновесным состоянием объекта то, что он не испытывает никакого ускорения (но может двигаться с постоянной скоростью).

Для поступательного движения равновесное состояние означает, что сумма всех сил, действующих на объект равна нулю:

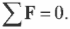
Иначе говоря, результирующая действующая сила равна нулю.

Вращательное движение также может быть равновесным, если такое движение происходит без углового ускорения, т.е. с постоянной угловой скоростью.

Для вращательного движения равновесное состояние означает, что сумма всех моментов сил, действующих на объект, равна нулю:

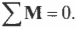
Как видите, это условие равновесного вращательного движения аналогично условию равновесного поступательного движения. Условия равновесного вращательного движения удобно использовать для определения момента силы, необходимого для уравновешивания неравномерно вращающегося объекта.

Простой пример: вешаем рекламный плакат

Предположим, что у входа в магазин нужно повесить большой и тяжелый рекламный плакат, как показано на рис. 10.9. Хозяин магазина пытался сделать это и раньше, но у него ничего не выходило, поскольку он использовал очень непрочный болт.

Попробуем определить силу, с которой болт должен удерживать всю конструкцию, показанную на рис. 10.9. Пусть плакат имеет массу 50 кг и висит на шесте 3 м от точки опоры шеста, а массу шеста в данном примере будем считать пренебрежимо малой. Болт находится в 10 см от точки опоры шеста.

Согласно условиям равновесия, сумма всех моментов сил должна быть равна нулю:

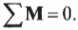
Иначе говоря:

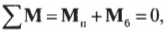
где ​( mathbf{M_п} )​ — это момент силы со стороны плаката, а ( mathbf{M_б} ) — это момент силы со стороны болта.

Чему равны упомянутые моменты? Момент силы со стороны плаката можно легко определить по формуле:

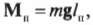
где ​( m )​ = 50 кг — это масса плаката, ​( mathbf{g} )​ — ускорение свободного падения под действием силы гравитационного притяжения (силы тяжести), ​( mmathbf{g} )​ — сила тяжести плаката, а ​( l_п )​ = 3 м — это плечо силы тяжести плаката.

Подставляя значения, получим:

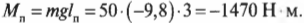
Обратите внимание, что здесь перед ускорением свободного падения под действием силы гравитационного притяжения стоит знак “минус”. Это значит, что вектор ускорения свободного падения направлен вниз, т.е. в сторону, противоположную выбранному направлению оси координат.

Момент силы со стороны болта определяется формулой:

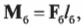
где ( mathbf{F_б} ) — это искомая сила, с которой болт должен удерживать всю конструкцию, а ( l_б ) = 0,1 м — это ее плечо.

Подставляя полученные выражения для моментов сил в формулу:

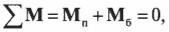
получим, что:

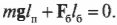
Отсюда с помощью простых алгебраических преобразований получим искомую силу:

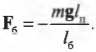
Как видите сила, с которой болт должен удерживать всю конструкцию, направлена противоположно вектору ускорения свободного падения, т.е. вверх.

Подставляя значения, получим искомый ответ:

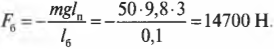
Более сложный пример: учитываем силу трения при расчете равновесия

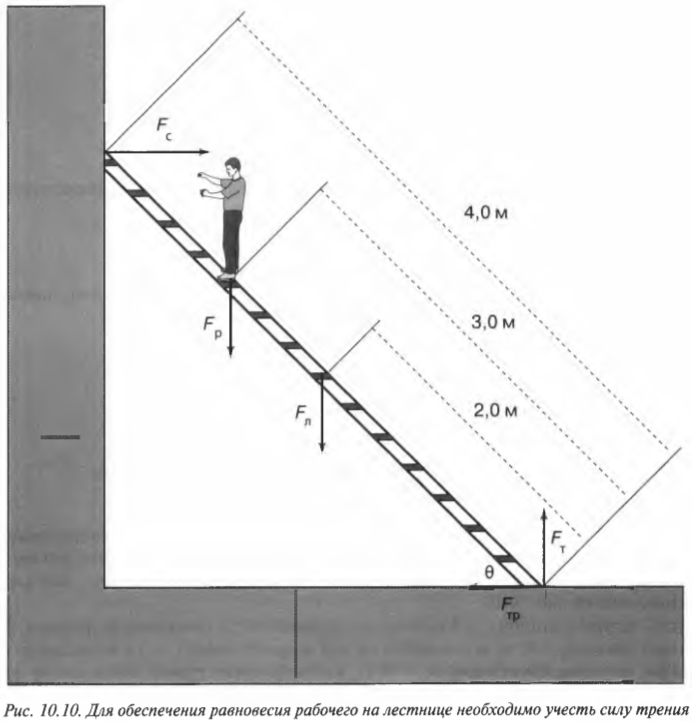
Рассмотрим теперь другую более сложную задачу, в которой для расчета равновесия системы объектов нужно учесть силу трения. Предположим, что работник магазина решил использовать переносную лестницу для монтажа рекламного плаката, как схематически показано на рис. 10.10.

Пусть лестница длиной ​( l_л )​ = 4 м стоит под углом ​( theta )​ = 45° к поверхности тротуара, работник имеет массу ​( m_р )​ = 45 кг и находится на ней на расстоянии ( l_р ) = 3 м от нижнего конца лестницы, лестница имеет массу (m_л ) = 20 кг, а коэффициент трения покоя между поверхностью тротуара и концами лестницы равен ​( mu_п )​ = 0,7. Вопрос: будет ли такая система объектов находиться в состоянии равновесия? Попросту говоря, достаточной ли будет сила трения, чтобы лестница вместе с рабочим не соскользнула и упала?

Итак, для ответа на этот вопрос нам нужно учесть следующие силы, действующие на лестницу:

• ​( mathbf{F_с} )​ — нормальная сила со стороны стены;
• ( mathbf{F_р} ) — вес рабочего;
• ( mathbf{F_л} ) — вес лестницы;
• ( mathbf{F_{тр}} ) — сила трения между поверхностью тротуара и концами лестницы;
• ( mathbf{F_т} ) — нормальная сила со стороны тротуара.

Согласно условиям равновесного поступательного движения, сумма всех сил, действующих на лестницу, должна быть равна нулю:

Это значит, что сумма всех сил вдоль горизонтальной оси, а именно нормальной силы со стороны стены ( mathbf{F_с} ) и силы трения между поверхностью тротуара и концами лестницы ( mathbf{F_{тр}} ), должна быть равна нулю, то есть:

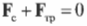
или

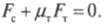
Перефразируя поставленный выше вопрос о достаточности силы трения, получим: выполняется ли условие

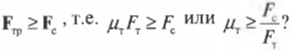
Кроме того, сумма всех сил вдоль вертикальной оси, а именно веса рабочего ( mathbf{F_р} ), веса лестницы ( mathbf{F_л} ) и нормальной силы со стороны тротуара ( mathbf{F_т} ), должна быть равна нулю, то есть:

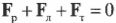
или

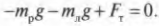
Согласно условиям равновесного вращательного движения, также необходимо равенство нулю всех моментов сил, действующих на лестницу:

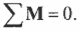
Пусть предполагаемой точкой вращения является нижний конец лестницы, тогда должна быть равна нулю сумма моментов сил, создаваемых весом рабочего ​( mathbf{M_р=[L_р!times! F_р]} )​, весом лестницы ( mathbf{M_л=[L_л!times!F_л]} ) и нормальной силой со стороны стены ( mathbf{M_с=[L_с!times! F_с]} ):

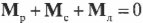
или

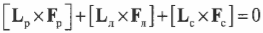
или

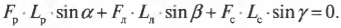
Поскольку ​( L_р=l_р )​, ​( L_л=l_л/2 )​ (центр тяжести лестницы находится посередине лестницы), ( L_с=l_л ), ​( alpha=360^{circ}-theta )​, ( beta=360^{circ}-theta ) и ​( gamma=theta )​, то получим:

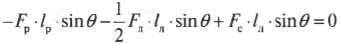
или

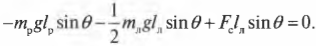
Таким образом, мы получили систему из двух уравнений с двумя неизвестными сил ( mathbf{F_с} ) и ( mathbf{F_т} ):

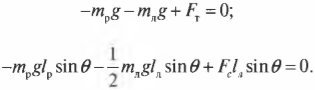
Зададимся вопросом: соблюдается ли условие

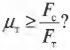
Из системы двух уравнений получим:

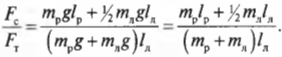
Итак, остается выяснить, соблюдается ли условие:

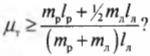
После подстановки значений получим:

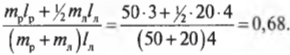
Поскольку ​( mu_т )​ = 0,7, то упомянутое условие соблюдается, и лестница с рабочим не упадет.

Момент силы

Это мера силы, которая может заставить объект вращаться вокруг оси.

Так же, как сила – это то, что заставляет объект ускоряться в линейной кинематике, так и крутящий момент – это то, что заставляет объект приобретать угловое ускорение.

Момент силы является векторной величиной. Направление вектора крутящего момента зависит от направления действия силы на ось.

Любой, кто когда-либо открывал дверь, обладает интуитивным пониманием крутящего момента. Когда человек открывает дверь, он толкает ту сторону двери, которая находится дальше всего от петель. Нажатие на сторону, ближайшую к петлям, требует значительно большего усилия. Хотя проделанная работа одинакова в обоих случаях (большее усилие будет применено на меньшем расстоянии).

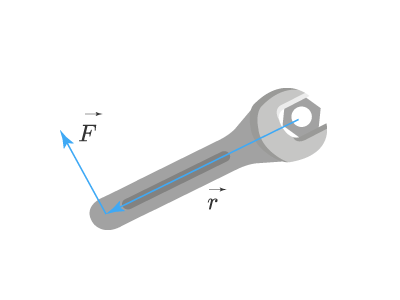
Виды моментов сил

Моменты сил могут быть статическими или динамическими.

Статический момент

Момент, который не производит угловое ускорение.

Кто-то, толкающий закрытую дверь, прикладывает статический момент к двери, потому что дверь не вращается вокруг своих петель, несмотря на прилагаемое усилие. Кто-то, крутящий велосипед на постоянной скорости, также прикладывает статический крутящий момент, потому что он не ускоряется.
Ведущий вал в гоночном автомобиле, ускоряющийся от линии старта, несет динамический крутящий момент, потому что он должен вызывать угловое ускорение колес, учитывая, что автомобиль ускоряется по трассе.

Как рассчитывается момент сил

Величина вектора момента сил (обозначается M→overrightarrow M), создаваемого данной силой FF является:

M  →=  [F→×r→]overrightarrow{M;}=;left[overrightarrow Ftimesoverrightarrow rright]

или, если раскрыть векторное уравнение, получится:

M  →=F→⋅r→sin⁡θoverrightarrow{M;}=overrightarrow Fcdotoverrightarrow rsintheta,

где rr – расстояние от оси вращение, до точки действия силы, θθ — угол, между векторами rr и FF.
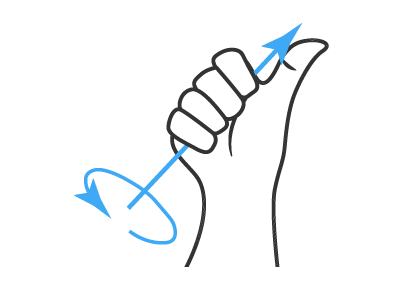
Направление вектора момента сил определяется с использованием правила правого захвата. Если рука вращается вокруг оси вращения пальцами, указывающими в направлении силы, то вектор момента сил указывает в направлении большого пальца, как показано на рисунке ниже.

Единица СИ для момента сил является Ньютон-метр.

Роль момента сил во вращательной кинематике

Во вращательной кинематике крутящий момент занимает место силы в линейной кинематике. Существует прямой эквивалент закона Ньютона второй (F=m⋅a)(F = m·a),

M=I⋅αM = I·α,

где αα – угловое ускорение. II – момент инерции, свойство вращающейся системы, которое зависит от распределения массы системы.

Чем больше II, тем сложнее для объекта получить угловое ускорение.

Тест по теме «Момент силы»