«Формула времени. Решение задач»
Скорость, время и расстояние — физические величины, взаимосвязаны процессом движения. Виды движений: 1) равномерное (прямолинейное, криволинейное и по окружности), 2) равноускоренное (с постоянным ускорением), 3) гармоническое. Для каждого вида движения своя формула времени.
Время обозначается как t. Единица измерения времени – с (секунды).
Самая простая формула при равномерном прямолинейном движении. Время, необходимое для прохождения пути равняется частному от деления пути на скорость равномерного прямолинейного движения: t = S / v.
При равноускоренном движении время равняется частному от деления разницы конечной и начальной скорости на ускорение: t = (v — v0) / a или частному от деления пути на разность конечной и начальной скорости: t = S / (v — v0).
Решение задач через формулу времени
Задача № 1.
Конькобежец может развивать скорость до 13 м/с. За какое время он пробежит дистанцию длиной 2,6 км?

Задача № 2.
Двигаясь с ускорением 5 м/с2 скорость космической ракеты увеличилась на 100 м/с. За какое время произошло такое изменение скорости?
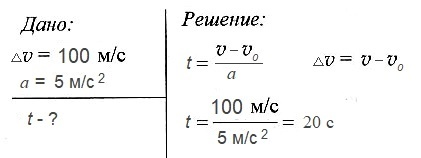
Задача № 3.
Пункты А и В находятся на берегу реки на некотором расстоянии друг от друга. Моторная лодка проходит расстояние АВ вниз по течению реки за время t1 = 3 ч, а плот то же расстояние – за время t0 =12 ч. Какое время t2 затратит моторная лодка на обратный путь?
Решение. Обозначим расстояние между пунктами А и В через L, скорость моторной лодки относительно воды через vл , а скорость течения через vт. Тогда t0 = L / vт , t1 = L / (vл + vт) , t2 = L / (vл — vт) . Исключая из записанной системы уравнений L, vл и vт
находим
Ответ: 6 ч.
Конспект урока «Формула времени. Решение задач».
Следующая тема: «».
Содержание:
- Определение и формула времени
- Особенности времени как физической величины
- Особенности времени как физической величины
- Единицы измерения времени
- Примеры решения задач
Определение и формула времени
В понятие времени отражаются такие свойства мира как постоянное развитие, изменение его в сознании человека. Процессы идут в определенной последовательности, при этом имеют определённую продолжительность.
Определение
Время – физическая величина, отражающая свойство материальных процессов иметь определенную продолжительность,
следовать друг за другом в установленной последовательности и развиваться этапно. Обозначают время буквой t.
Особенности времени как физической величины
Время неотделимо от материи и ее движения, так как является ее формой существования. Нет смысла говорить о времени самом по себе, так как в отрыве от материальных процессов течение времени становится бессодержательным. Только исследование процессов, происходящих в материальном мире и их взаимосвязей, делает понятие времени физически содержательным.
В череде процессов, происходящих в природе, особенное место занимают повторяющиеся процессы (повторение дней и ночей, дыхание, перемещение звезд по небосводу и т. д). Исследование и сравнение подобных процессов между собой ведет к идее о длительности материальных процессов, сравнение их длительности приводит к идее об их измерении.
Эталоном измерения является периодический процесс, который называют часами. Существуют системы отсчета, в которых возможно введение единого времени с достаточной для практики точностью. Введение единого времени хорошо подтверждается экспериментом. Теория дает возможность предсказать отклонения единого времени, что можно проверить эмпирически.
Длительность физического процесса, который происходит в некоторой точке, определяют при помощи часов, которые располагают в той же точке. При этом применяется прямое сравнение, сравниваются длительности процессов, которые текут в одной точке. Измерение длительности сводят к фиксации начала и окончания рассматриваемого процесса на шкале процесса, который принимают за эталонный. При этом говорят как о фиксации показаний часов в момент начала и окончания процесса, и это не имеет отношения к фактическому месту нахождения часов (процесса) в точке рассмотрения.
Синхронизация часов и изучения законов распространения физических сигналов развивались параллельно, при этом происходили взаимные уточнения и дополнения. Синхронизацию проводят при помощи сигналов, которые распространяются с конечной скоростью. Этот метод использует определение постоянной скорости: если из точки, в которой часы показывают t0, исходит сигнал, перемещающийся со скоростью v=const, то тогда, когда сигнал придет в точку на расстоянии s, часы в этой точке должны показать время:
$$t=t_{0}+frac{s}{v}(1)$$
Такая синхронизация согласуется с синхронизацией с использованием световых сигналов. Тогда часы синхронизируются по формуле:
$$t=t_{0}+frac{s}{c}(2)$$
где c=299792,4562 км/с – скорость света, которая не зависит от скорости источника и приемника по всем направлениям пространства одинакова.
Особенности времени как физической величины
Перемещение ($bar{s}$), равно:
$$bar{s}left(t_{2}, t_{1}right)=bar{s}left(t_{2}right)-bar{s}left(t_{1}right)(3)$$
где $bar{s}(t_2)$ – радиус-вектор в момент времени
$t_2, bar{s}(t_1)$ – радиус-вектор в момент времени
$t_1$ .
Мгновенная скорость ($bar{v}$):
$$bar{v}=frac{d bar{s}}{d t}(4)$$
Мгновенное ускорение ($bar{a}$):
$$bar{a}=frac{d bar{v}}{d t}(5)$$
Единицы измерения времени
Основной единицей измерения момента силы в системах СИ и СГС является: [t]=c
Единицы измерения времени основываются на периоде вращения Земли около своей
оси и вокруг Солнца, Луни вокруг Земли. Внесистемные единицы измерения времени: час, минута, сутки и т.д.
Примеры решения задач
Пример
Задание. Движения двух тел заданы уравнениями: и s1(t)=5t и s2(t)=150-10t. Найдите время встречи.
Решение. В точке встречи s1(t)=s2(t). Приравняем правые части функцийx(t), имеем:
$$5 t=150-10 t rightarrow 15 t=150 rightarrow t=10$$
Ответ. t=10 c

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Движение материальной точки, задано уравнением: x=4t-0,05t2 .
В какой момент времени, скорость точки равна нулю? Коэффициенты имеют размерности: 4 м/с, 0,05м/с2 .
Изобразите графики зависимости модуля ускорения от времени.
Решение. В условиях задачи задана функция x(t), скорость можно найти как:
$$v=frac{d x}{d t}=4-0,1 t(2.1)$$
Приравняем скорость к нулю, найдем время:
$$4-0,1 t=0 rightarrow t=frac{4}{0,1}=40(c)$$
Определим, какова зависимость модуля ускорения от времени, для этого возьмем производную по времени от функции v(t) (2.1):
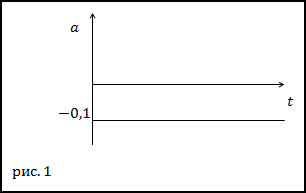
$$a(t)=frac{d v}{d t}=-0,1(2.2)$$
Тогда график зависимости a(t) имеет вид:
Ответ. t=40 c
Читать дальше: Формула длины волны.
Формулы скорости, времени, расстояния?
Как выразить эти понятия друг одно через другие?
Анонимный вопрос
2 ноября 2018 · 236,8 K
Если вам известна скорость v и время t, то вы сможете найти расстояние S по формуле S=vt.
Обратите внимание на единицы измерения! Если вам дана скорость в километрах в час, то и время должно быть выражено в часах (или в метрах в секунду и секундах соответственно).
Выразить скорость из этой формулы можно следующим образом: v=S/t
А если вы хотите посчитать время, то воспользуйтесь формулой t=S/v
204,1 K
Комментировать ответ…Комментировать…
V = S : t
t = S : V
S = V * t
S = расстояние
V = скорость
t = время
: = деление
* = умножение
Пример :
Решил найти расстояние ( S)
Для этого скорость ( V) которая равна 4км/ч *время ( t) 4 часа
Ответ : 16 км Читать далее
21,3 K
Подскажите а как посчитать, за если я прохожу допустим растояние 9 метров за 7 минут, то за сколько я пройду 300 метров?
Комментировать ответ…Комментировать…
Учусь в гимназии №17. Увлекаюсь математикой, русским языком, родным языком, литературой и… · 20 мая 2021
(Обратите внимание, что для записи формулы пути используются строчные буквы s, v и t. Это сделано, чтобы не путать их с обозначением площади — S и объёма — V.) Читать далее
20,1 K
Комментировать ответ…Комментировать…
Чтобы найти скорость, нужно расстояние разделить на время движения: v = S: t. Время – это продолжительность каких-то действий, событий. Время движения обозначается маленькой латинской буквой t. Чтобы найти время, нужно расстояние разделить на скорость движения: t = S: v. Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
5,7 K
Комментировать ответ…Комментировать…
Короче!
Если у вас расстояние нужно найти то:
S=t*v, S=50*20(пример)
Если нужно найти время то:
t=S:V
Если нужно найти скорость то :
V=S:T.
Это все формулы. Читать далее
59,9 K
спасибо, Warrior! Было не понятно, но
ты помог мне выровнять математику!
Комментировать ответ…Комментировать…
На прошлых уроках мы познакомились с определением механического движения, узнали, каким бывает движение, изучили его свойства и характеристики. Теперь нам известны формулы для расчета скорости при равномерном движении ($upsilon = frac{S}{t}$) и средней скорости при неравномерном ($upsilon_{ср} = frac{S}{t}$).
На данном уроке мы посмотрим на эти формулы с другой стороны — научимся использовать их для расчета пути и времени движения, а также рассмотрим графики скорости и пути для равномерного движения.
Формулы для расчета пути и времени движения при равномерном движении тела
Скорость тела при равномерном движении вычисляется по формуле $upsilon = frac{S}{t}$. Отсюда, если мы знаем скорость и время, то можем найти пройденный путь:
$S = upsilon t$.
Чтобы определить путь, пройденный телом при равномерном движении, нужно скорость тела умножить на время его движения.
Выразим время:
$t = frac{S}{upsilon}$.
Чтобы рассчитать время при равномерном движении, нужно путь, пройденный телом, разделить на скорость его движения.
Формулы для расчета пути и времени движения при неравномерном движении тела
При неравномерном движении мы используем определение средней скорости, которую можем найти по формуле:
$upsilon_{ср} = frac{S}{t}$.
Чтобы определить путь при неравномерном движении, нужно среднюю скорость движения умножить на время:
$large S = upsilon_{ср} t$.
Также мы можем рассчитать время, разделив путь, пройденный телом, на среднюю скорость его движения:
$t = frac{s}{upsilon_{ср}}$.
График скорости равномерного движения
Так как скорость – это векторная величина, она характеризуется и модулем, и направлением. В зависимости от выбранного направления скорость по знаку может быть как положительной, так и отрицательной.
На рисунке 1 изображен динозавр, автомобиль и дом. Зададим ось координат $x$.
Если динозавр начнет двигаться к дому, то его скорость будет положительной, так как направление движения совпадает с направлением оси $x$. Если же динозавр направится к автомобилю, то его скорость будет отрицательной, так как направление движения противоположно направлению оси $x$.
Итак, график скорости равномерного движения имеет вид, представленный на рисунке 2.
Из графика видно, что скорости с течением времени не изменяется – они постоянны в любой выбранный момент времени. Если мы посмотрим на график положительной скорости, то увидим, что $upsilon = 6 frac{м}{с}$, на график отрицательной — $upsilon = -4 frac{м}{с}$.
Зная скорость и время, мы можем рассчитать пройденный путь за определенный промежуток времени. Рассчитаем какой путь пройдет тело с положительной скоростью за $4 space с$.
$S = upsilon t = 6 frac{м}{с} cdot space 4 c = 24 space м$.
График пути равномерного движения
Пример графика зависимости пути равномерного движения представлен на рисунке 3.
Здесь $S$ — ось пройденных путей, $t$ — ось времени. По этому графику мы можем найти путь, пройденный телом за определенный промежуток времени. Например, за 1 с тело проходит путь длиной 2 м, за 2 с – 4 м, за 3 с – 6 м.
Зная путь и время, мы можем рассчитать скорость. Для удобства расчета возьмем самый первый отрезок пути: $t = 1 space с$, $S = 2 space м$. Тогда,
$upsilon = frac{S}{t} = frac{2 space м}{1 space с} = 2 frac{м}{с}$.
Задачи
Задача №1
Самым быстрым животным на Земле считается гепард. Он способен развивать скорость до $120 frac{км}{ч}$, но сохранять ее способен в течение короткого промежутка времени. Если за несколько секунд он не настигнет добычу, то, вероятнее всего, уже не сможет ее догнать. Найдите путь, который пробежит гепард на максимальной скорости за $3$ секунды.
Переведем единицы измерения скорость в СИ и решим задачу.
$120 frac{км}{ч} = 120 cdot frac{1000 space м}{3600 space с} approx 33 frac{м}{с}$.
Дано:
$upsilon = 120 frac{км}{ч}$
$t = 3 space c$
СИ:
$upsilon = 33 frac{м}{с}$
$S — ?$
Показать решение и ответ
Скрыть
Решение:
Гепард двигается равномерно в течение 3 с.
Путь, который он проходит за это время:
$S = upsilon t$,
$S = 33 frac{м}{с} cdot 3 с approx 100 space м$
Ответ: $S = 100 space м$.
Задача №2
Колибри – самые маленькие птицы на нашей планете. При полете они совершают около 4000 взмахов в минуту. Тем не менее, они способны пролетать очень большие расстояния. Например, некоторые виды данной птицы перелетают Мексиканский залив длиной $900 км$ со средней скоростью $40 frac{км}{ч}$. Сколько времени у них занимает такой полет?
Переведем единицы измерения скорость в СИ и решим задачу.
$40 frac{км}{ч} = 40 cdot frac{1000 м}{3600 с} approx 11 frac{м}{с}$,
$900 space км = 900 space 000 м$.
Дано:
$upsilon_{ср} = 40 frac{км}{ч}$
$S = 900 space км$
CИ:
$upsilon_{ср} = 11 frac{м}{с}$
$S = 900 space 000 space м$
$t-?$
Показать решение и ответ
Скрыть
Решение:
Полет колибри будет примером неравномерного движения. Зная среднюю скорость и путь, рассчитаем время перелета:
$t = frac{s}{upsilon_{ср}}$,
$t = frac{900 space 000 space м}{11 frac{м}{с}} approx 82 space 000 space с$.
Переведем время в часы:
$1 space ч = 60 space мин = 60 cdot 60 space c = 3600 space c$.
Тогда:
$t = frac{82 space 000 space c}{3600 space c} approx 23 space ч$.
Ответ: $t = 23 space ч$.
Больше задач на расчет пути и времени движения с подробными решениями смотрите в отдельном уроке.
Упражнения
Упражнение №1
Пользуясь таблицей 1 из прошлого урока, найдите скорости страуса, автомобиля, искусственного спутника Земли. Определите пути, пройденные ими за $5 space с$.
Дано:
$upsilon_1 = 22 frac{м}{с}$
$upsilon_2 = 20 frac{м}{с}$
$upsilon_3 = 8000 frac{м}{с}$
$t = 5 space с$
$S_1 — ?$
$S_2 — ?$
$S_3 — ?$
Показать решение и ответ
Скрыть
Решение:
Путь, пройденный страусом:
$S_1 = upsilon_1 t$,
$S_1 = 22 frac{м}{с} cdot 5 space с = 110 space м$.
Путь, пройденный автомобилем:
$S_2 = upsilon_2 t$,
$S_2 = 20 frac{м}{с} cdot 5 space с = 100 space м$.
Путь, пройденный искусственным спутником Земли:
$S_3 = upsilon_3 t$,
$S_3 = 8000 frac{м}{с} cdot 5 space с = 40 space 000 space м = 40 space км$.
Ответ: $S_1 = 110 space м$, $S_2 = 100 space м$, $S_3 = 40 space км$.
Упражнение №2
На велосипеде можно без особого напряжения ехать со скоростью $3 frac{м}{с}$. На какое расстояние можно уехать за $1.5 space ч$?
Дано:
$t = 1.5 space ч$
$upsilon = 3 frac{м}{с}$
СИ:
$t = 5400 space с$
$S — ?$
Показать решение и ответ
Скрыть
Решение:
Рассчитаем путь, который можно проехать на велосипеде с указанной скоростью:
$S = upsilon t$,
$S = 3 frac{м}{с} cdot 5400 space с = 16 space 200 space м = 16.2 space км$.
Ответ: $S = 16.2 space км$.
Упражнение №3
На рисунке 4 показан график зависимости пути равномерного движения тела от времени ($S$ — ось пройденного пути, $t$ — ось времени). По этому графику найдите, чему равен путь, пройденный телом за $2 space ч$. Затем рассчитайте скорость тела.
Определим из графика путь, пройденный телом за $2 space ч$. Этому времени на графике соответствует значение пути, равное $200 space км$. Запишем условие задачи и решим ее.
Дано:
$S = 200 space км$
$t = 2 space ч$
$upsilon — ?$
Показать решение и ответ
Скрыть
Решение:
Скорость равномерного движения рассчитываем по формуле:
$upsilon = frac{S}{t}$.
$upsilon = frac{200 space км}{2 space ч} = 100 frac{км}{ч}$.
Ответ: $upsilon = 100 frac{км}{ч}$.
Упражнение №4
График зависимости скорости равномерного движения тела от времени представлен на рисунке 5. По этому графику определите скорость движения тела. Рассчитайте путь, который пройдет тело за $2 space ч$, $4 space ч$.
Из графика видно, что скорость тела равна $8 frac{м}{с}$. Этот график представляет собой прямую, параллельную оси времени, потому что движение равномерное, и скорость тела не изменяется с течением времени. Запишем условие задачи и решим ее.
Дано:
$t_1 = 2 space ч$
$t_2 = 4 space ч$
$upsilon = 8 frac{м}{с}$
СИ:
$t_1 = 7200 space с$
$t_2 = 14 space 400 space с$
$S_1 — ?$
$S_2 — ?$
Показать решение и ответ
Скрыть
Решение:
Путь рассчитаем по формуле: $S = upsilon t$.
За $2 space ч$ тело пройдет путь:
$S_1 = upsilon t_1$,
$S_1 = 8 frac{м}{с} cdot 7200 space с = 57 space 600 space м = 57.6 space км$.
За $4 space ч$ тело пройдет путь:
$S_2 = upsilon t_2$,
$S_2 = 8 frac{м}{с} cdot 14 space 400 space с = 115 space 200 space м = 115.2 space км$.
Ответ: $S_1 = 57.6 space км$, $S_2 = 115.2 space км$.
Упражнения №5
По графикам зависимости путей от времени (рисунок 6) двух тел, движущихся равномерно, определите скорости этих тел. Скорость какого тела больше?
Для того, чтобы рассчитать скорость тела, нам нужно знать путь и время, за которое этот путь был пройден. Возьмем эти значения для двух тел из их графиков. Первое тело (I) проходит путь, равный $4 space м$, за $2 space с$. Второе тело (II) проходит путь, равный $4 space м$, за $4 space с$. Запишем условие задачи и решим ее.
Дано:
$S = 4 space м$
$t_1 = 2 space с$
$t_2 = 4 space с$
$upsilon_1 — ?$
$upsilon_2 — ?$
Показать решение и ответ
Скрыть
Решение:
Рассчитаем скорость первого тела:
$upsilon_1 = frac{S}{t_1}$,
$upsilon_1 = frac{4 space м}{2 space с} = 2 frac{м}{с}$.
Рассчитаем скорость второго тела:
$upsilon_2 = frac{S}{t_2}$,
$upsilon_2 = frac{4 space м}{4 space с} = 1 frac{м}{с}$.
Получается, что скорость первого тела больше скорости второго.
Ответ: $upsilon_1 = 2 frac{м}{с}$, $upsilon_2 = 1 frac{м}{с}$, $upsilon_1 > upsilon_2$.