Памятка
«Учимся решать задач на движение»
В
задачах на движение рассматриваются
три взаимосвязанные величины:
S
– расстояние (пройденный путь),
t
– время движения и
V
– скорость – расстояние, пройденное за
единицу времени.
Расстояние – это
произведение скорости на время движения
S
= V ● t
Скорость – это
частное от деления расстояния на время
движения
V
= S : t
Время – это частное
от деления расстояния на скорость
движения
t
= S
: V
Задачи
на встречное движение
Если два тела
одновременно движутся навстречу друг
другу, то расстояние между ними постоянно
изменяется на одно и то же число, равное
сумме расстояний, которые проходят тела
за единицу времени.
Скорость сближения –
это сумма скоростей, движущихся навстречу
друг другу тел.
V сближ.
= 1V + 2V
Пример
1.
Два велосипедиста одновременно выехали
навстречу друг другу из двух посёлков
и встретились через 3 часа. Первый
велосипедист ехал со скоростью 12 км/ч,
а второй – 14 км/ч. На каком расстоянии
находятся посёлки?
Схема к задаче:

Решение:
S
= V ● t
V
сближ. = 1V + 2V
1
способ:
1)
12 • 3 = 36 (км) – проехал первый велосипедист
до встречи
2)
14 • 3 = 42 (км) – проехал второй велосипедист
до встречи
3)
36 + 42 = 78 (км)
2
способ:
1)
12 + 14 = 26 (км/ч) – скорость сближения
2)
26 • 3 = 78 (км)
Ответ:
расстояние между посёлками 78 км.
Пример
2.
Из двух городов навстречу друг другу
выехали две машины. Скорость первой –
80 км/ч, скорость второй – 60 км/ч. Через,
сколько часов машины встретятся, если
расстояние между городами 280 км?
Схема к задаче:

Решение:
V
сближ. = 1V
+ 2V
t
= S
: V
1)
80 + 60 = 140 (км/ч) – скорость сближения
2)
280 : 140 = 2 (ч)
Ответ:
машины
встретятся
через 2 часа.
Пример
3.
Из двух городов, расстояние между
которыми 340 км, выехали одновременно
навстречу друг другу две машины. Скорость
первой – 80 км/ч. С какой скоростью ехала
вторая машина, если встретились они
через 2 часа?
Схема к задаче:

Решение:
V
= S : t
2V
= V
сближ. – 1V
1)
340 : 2 = 170 (км/ч) – скорость сближения
2)
170 – 80 = 90 (км/ч)
Ответ:
90 км/ч. скорость второй машины
Задачи
на движение в противоположных направлениях
Если два тела
одновременно движутся в противоположных
направлениях, то расстояние между ними
постепенно увеличивается.
Скорость удаления
– это расстояние, которое проходят тела
за 1 ч при движении в противоположных
направлениях. V
удал. = 1V + 2V
Пример
1. Два
лыжника одновременно вышли из пункта
А в противоположных направлениях. Первый
лыжник шёл со скоростью 12 км/ч, а второй
– 14 км/ч. На каком расстоянии друг от
друга они будут через 3 ч?
Схема к задаче:

Решение:
S
= V ● t
1
способ
1)12
• 3 = 36 (км) – расстояние, которое прошёл
первый лыжник за 3 ч
2)14
• 3 = 42 (км) – расстояние, которое прошёл
второй лыжник за 3 ч
3)36
+ 42 = 78 (км)
2
способ
V
удал. = 1V
+ 2V
S
= V ● t
1)12
+ 14 = 26 (км/ч) – скорость удаления
2)26
• 3 = 78 (км)
Ответ:
через
3 ч
они
будут друг от друга на расстоянии 78
км.
Пример
2. Из города
в противоположных направлениях выехали
две машины. Скорость первой – 80 км/ч,
скорость второй – 60 км/ч. Через сколько
часов расстояние между машинами будет
280 км?
Схема к задаче:

Решение:
V
удал. = 1V
+ 2V
t
= S
: V
1)
80 + 60 = 140 (км/ч) – скорость удаления
2)
280 : 140 = 2 (ч)
Ответ:
через 2 часа расстояние
между машинами будет 280 км
Пример 3.
Из города одновременно в противоположных
направлениях выехали две машины. Скорость
первой – 80 км/ч. С какой скоростью ехала
вторая машина, если через 2 часа расстояние
между ними было 340 км?
Схема к задаче:

Решение:
V
= S : t
2V
=
V
удал. – 1V
1)
340 : 2 = 170 (км/ч) – скорость удаления машин
2)
170 – 80 = 90 (км/ч)
Ответ:
скорость второй машины 90 км/ч.
Задачи
на движение в одном направлении
Пример
1. Автомобиль за 2 ч проехал 192 км.
Следующие 3 ч он двигался со скоростью
на 6 км/ч меньше. Сколько всего километров
проехал автомобиль?
Схема
к задаче:

Решение:
1)192
: 2 = 96 (км/ч) – первая скорость
2)96
– 6 = 90 (км/ч) – вторая скорость
3)90
• 3 = 270 (км) – второе расстояние
4)192
+ 270 = 462 (км)
Ответ:
462 км.
Пример
2. Из двух пунктов, расстояние между
которыми 24 км, одновременно вышел
спортсмен и выехал велосипедист. Скорость
спортсмена 6 км/ч., а скорость велосипедиста
18 км/ч..
1).Через
сколько часов велосипедист догонит
спортсмена?
2).На
каком расстоянии от пункта В велосипедист
догонит спортсмена?
3).
На сколько километров путь велосипедиста
больше пути спортсмена?






18 км/ч
6 км/ч ?


24 км
Решение:
V
приближ. = 2V
-1V
, где 2V
ֺ
>
1V
t
= S
: V
1).
18 – 6 = 12 (км /ч.) – скорость приближения
велосипедиста и спортсмена
2).
24 : 12 = 2 (ч.) – время, через которое
велосипедист догонит спортсмена.
3).
6 ●2 = 12 (км) – расстоянии, на котором
велосипедист догонит спортсмена.
Ответ:
через 2 часа; 12 км.
Пример
3. За какое время мотоцикл догонит
грузовой автомобиль, если расстояние
между ними 45 км, а скорость мотоцикла
больше скорости грузовика на 15 км/ч?

Решение:
45
: 15 = 3 (ч)
Ответ:
через 3 часа.

Чтобы решать задачи на встречное движение, вспомним основные понятия и формулы для решения задач на движение:
(v) — скорость;
и
v2
— скорость первого и второго объектов;
— скорость сближения;
(t) — время;
— время до встречи;
(s) — первоначальное расстояние;
— расстояние между объектами через определённый промежуток времени после начала движения объектов.
Рассмотрим первую ситуацию.

Яра и Юра давно не виделись и договорились встретиться в парке. Расстояние между друзьями составляет (315) км. Юра поехал на автомобиле со скоростью (60) км/ч, а Яра — на автобусе со скоростью (45) км/ч.
Через какое время друзья встретятся?
Начертим схему.

Стрелки на схеме показывают, с какой скоростью едут Юра и Яра. Флажком обозначено место встречи друзей. А дугой показано расстояние между героями — (315) км.
По схеме видно, что друзья едут навстречу друг другу, то есть расстояние между ними сокращается. Перед нами — встречное движение.
Первоначально необходимо найти скорость сближения по формуле:

1. (60 + 45 = 105) км/ч.
Теперь найдём, через какое время произойдёт встреча Юры и Яры:
2. (315 : 105 = 3) ч.
Ответ: через (3) часа друзья встретятся в парке.
Рассмотрим вторую ситуацию.

С двух станций одновременно начали движение два поезда навстречу друг другу. Скорость первого поезда равна (90) км/ ч, а второго — (70) км/ч. Чему равно расстояние между станциями, если встреча поездов произошла через (2) часа после начала отправления?
Начертим схему.

Найдём скорость сближения двух поездов: (90 + 70 = 160) км/ч.
Определим расстояние между станциями до начала отправления поездов: (160 · 2 = 320) км.
Ответ: расстояние между станциями составляет (320) км.
Рассмотрим третью ситуацию.

Тракторист и таксист едут навстречу друг другу из двух сёл, расстояние между которыми составляет (400) км. Скорость трактора — (25) км/ ч, а такси — (50) км/ч. Как изменится расстояние между ними через (1) час? Через (2) часа? Через (4) часа?
Заполним таблицу:
|
(t) ч |
(d) км |
|
(0) |
(400) |
|
(1) |
(400) (– (25 + 50) · 1 = 325) |
|
(2) |
(400) (– (25 + 50) · 2 = 250) |
|
(4) |
(400) (– (25 + 50) · 4 = 100) |
Источники:
Изображения: схема, робот, космонавт, транспорт. © ЯКласс.
Тип 1
Задача 1. Две девочки вышли одновременно навстречу друг другу из своих домов. Они встретились через 8 мин. Одна шла со скоростью 60 м/мин, а другая – 70 м/мин. Каково расстояние между домами девочек?
Краткая запись:
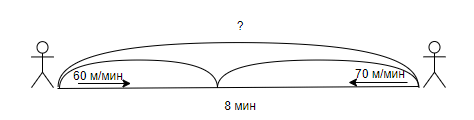
Решение:
- 60х8=480 (м) прошла первая девочка;
- 70х8=560 (м) прошла вторая девочка;
- 480+560=1040 (м) прошли обе девочки.
Ответ: 1040 м расстояние между домами девочек.
Тип 2
Задача 2. Два пешехода вышли одновременно из двух деревень навстречу друг другу. Один пешеход шёл со скоростью 5 км/ч, другой – 4 км/ч. Через сколько часов они встретятся, если расстояние между деревнями равно 36 км?
Краткая запись:
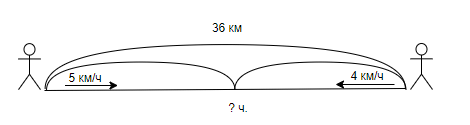
Решение:
- 5+4=9 (км/ч) скорость сближения;
- 36:9=4 (ч) идет каждая девочка.
Ответ: через 4 часа девочки встретятся.
Тип 3
Задача 3. Два лыжника вышли одновременно навстречу друг другу из двух пунктов, расстояние между которыми 66 км. Скорость одного лыжника 12 км/ч. С какой скоростью шёл второй лыжник, если они встретились через 3 ч?
Краткая запись:
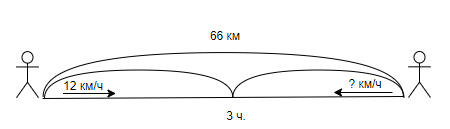
Решение:
- 12х3=36 (км) прошел первый лыжник;
- 66-36=30 (км) прошел второй лыжник:
- 30:3=10 (км/ч) скорость второго лыжника.
Ответ: со скоростью 10 км/ч шёл второй лыжник.
Тип 4
Задача 4. Два лыжника вышли одновременно навстречу друг другу из двух пунктов, расстояние между которыми 44 км. Первый лыжник шёл со скоростью 12 км/ч и прошёл до встречи 24 км. С какой скоростью шёл второй лыжник?
Краткая запись:
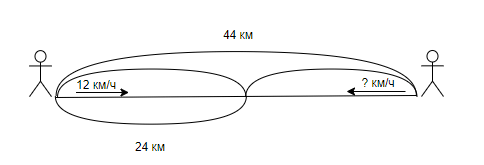
Решение:
- 24:12=2 (ч) шел до встречи первый лыжник;
- 44-24=20 (км) расстояние, которое прошел второй лыжник:
- 20:2=10 (км/ч) скорость второго лыжника.
Ответ: со скоростью 10 км/ч шёл второй лыжник.
Тип 5
Задача 5. Два пешехода одновременно вышли из двух деревень и пошли навстречу друг другу. Один пешеход шёл со скоростью 5 км/ч и прошёл до встречи 15 км. Другой пешеход шёл со скоростью 4 км/ч. Какое расстояние до встречи прошёл второй пешеход?
Краткая запись:
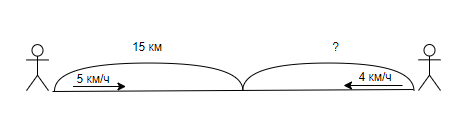
Решение:
- 15:5=3 (ч) шел до встречи первый пешеход;
- 4х3=12 (км) расстояние, которое прошел второй пешеход.
Ответ: 12 км до встречи прошёл второй пешеход.
Задачи на встречное движение
Рассмотрим задачи, в которых речь идёт о встречном движении. В таких задачах два каких-нибудь объекта движутся навстречу друг другу. Задачи на встречное движение можно решать двумя способами.
Задача 1. Два автомобиля выехали одновременно из двух населённых пунктов и встретились через 4 часа. Первый автомобиль ехал со скоростью 100 км/ч, а второй — со скоростью 70 км/ч. На каком расстоянии друг от друга находятся населённые пункты?

Решение: Из условия задачи известны скорость каждого автомобиля и время, которое автомобили были в пути. Значит, можно найти расстояние, которое проехал каждый автомобиль до встречи. Для этого нужно скорость умножить на время:
1) 100 · 4 = 400 (км) — проехал первый автомобиль,
2) 70 · 4 = 280 (км) — проехал второй автомобиль.
Найдя сумму полученных результатов, узнаем расстояние между населёнными пунктами:
400 + 280 = 680 (км).
Данную задачу можно решить и другим способом. Каждый час расстояние между автомобилями сокращалось на 170 километров (100 + 70), 170 км/ч — это скорость сближения автомобилей. За 4 часа они проехали расстояние:
170 · 4 = 680 (км).
Таким образом, задачу на встречное движение можно решить двумя способами:
| 1-й способ: | 2-й способ: |
|---|---|
| 1) 100 · 4 = 400 (км) | 1) 100 + 70 = 170 (км/ч) |
| 2) 70 · 4 = 280 (км) | 2) 170 · 4 = 680 (км) |
| 3) 400 + 280 = 680 (км) |
Ответ: Населённые пункты находятся на расстоянии 680 км.
Задача 2. Из двух посёлков навстречу друг другу вышли одновременно два пешехода. Скорость первого пешехода 4 км/ч, а скорость второго пешехода 5 км/ч. Какое расстояние будет между пешеходами через 5 часов после выхода, если расстояние между посёлками 70 км?

Решение: Сначала можно определить сколько километров прошёл каждый из пешеходов за 5 часов, для этого скорость пешеходов умножим на 5:
1) 4 · 5 = 20 (км) — прошёл первый пешеход,
2) 5 · 5 = 25 (км) — прошёл второй пешеход.
Затем можно найти общий путь, пройденный двумя пешеходами за 5 часов:
20 + 25 = 45 (км).
Теперь можно найти расстояние между пешеходами, отняв от общего расстояния между посёлками 45 уже пройденных километров:
70 – 45 = 25 (км).
У данной задачи есть и второй вариант решения. Можно сначала найти скорость сближения пешеходов:
4 + 5 = 9 (км/ч).
Затем найти пройденное расстояние, умножив скорость сближения (9 км/ч) на время движения пешеходов (5 ч):
9 · 5 = 45 (км).
А теперь, для нахождения расстояния между пешеходами, вычесть пройденное расстояние (45 км) из общего:
70 – 45 = 25 (км).
Таким образом, данная задача имеет два варианта решения:
| 1-й способ: | 2-й способ: |
|---|---|
| 1) 4 · 5 = 20 (км) | 1) 4 + 5 = 9 (км/ч) |
| 2) 5 · 5 = 25 (км) | 2) 9 · 5 = 45 (км) |
| 3) 20 + 25 = 45 (км) | 3) 70 – 45 = 25 (км) |
| 4) 70 – 45 = 25 (км) |
Ответ: Через 5 часов расстояние между пешеходами будет 25 км.
 Задачи на движение (скорость, время и расстояние) являются одной из основных типов задач по математике, которые должен уметь решать каждый школьник. В данной статье рассмотрены все типы задач на движение:
Задачи на движение (скорость, время и расстояние) являются одной из основных типов задач по математике, которые должен уметь решать каждый школьник. В данной статье рассмотрены все типы задач на движение:
— простые задачи на скорость, время и расстояние;
— задачи на встречное и противоположное движение;
— задачи на движение в одном направлении (на сближение и удаление);
— решение задач на движение по реке.
Скорость, время и расстояние: определения, обозначения, формулы
скорость = расстояние: время — формула нахождения скорости;
время = расстояние: скорость — формула нахождения времени;
расстояние = скорость · время — формула нахождения расстояния.
Скорость – это расстояние, пройденное за единицу времени: за 1 секунду, за 1 минуту, за 1 час и так далее.
Пример обозначения: 7 км/ч (читается: семь километров в час).
Если весь путь проходится с одинаковой скоростью, то такое движение называется равномерным.
На сайте представлены калькуляторы онлайн, с помощью которых можно перевести скорость, время и расстояние в другие единицы измерения:
1.Конвертер единиц измерения скорости
2.Конвертер единиц измерения времени
3.Конвертер единиц измерения расстояния (длины)
Примеры простых задач.
Задача 1.
Автомобиль проехал 180 км за 2 часа. Чему равна скорость автомобиля?
Решение: 180:2=90 (км/ч.)
Ответ: Скорость автомобиля равна 90 км/ч.
Задача 2.
Автобус проехал путь в 240 км со скоростью 80 км/ч. Сколько времени ехал автобус?
Решение: 240:80=3 (ч.)
Ответ: Автобус проехал 3 часа.
Задача 3.
Грузовик ехал 5 часов со скоростью 70 км/ч. Какое расстояние проехал грузовик за это время?
Решение: 70 · 3 = 350 (км)
Ответ: Грузовик за 5 часов проехал 350 км.
Задачи на встречное движение
В таких задачах два объекта движутся навстречу друг другу.
Задачи на встречное движение можно решать двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость сближения объектов (как сумму их скоростей), общие время и расстояние. Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Задача 4.
Из двух пунктов навстречу друг другу одновременно выехали два поезда и встретились через 3 часа. Первый поезд ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. На каком расстоянии друг от друга находятся пункты?
Решение:
Первый способ. Найти расстояние, которое проехал каждый автобус, и сложить полученные данные:
80*3=240 (км) – проехал 1й автобус, 70*3=210 (км) – проехал 2й поезд,
240+210=450 (км) – проехали два поезда.
Второй способ. Найти скорость сближения поездов, то есть на сколько сокращалось расстояние между ними каждый час; а затем найти расстояние:
80+70=150 (км/ч), 150*3=450 (км).
Ответ: города находятся на расстоянии 450 км.
Задача 5.
Из двух городов навстречу друг другу одновременно выехали два автобуса. Первый автобус ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. Какое расстояние будет между ними через 2 часа, если расстояние между городами 450 км?
Решение:
Первый способ. Определить, сколько километров проехал каждый автобус и найти расстояние, которое осталось проехать:
80*2=160 (км)-проехал 1й автобус, 70*2=140 (км)-проехал 2й автобус,
160+140=300 (км)-проехали два автобуса, 450-300=150 (км)-осталось проехать.
Второй способ. Найти скорость сближения автобусов и умножить ее на время в пути.
80*70=150 (км/ч) – скорость сближения; 150*2=300 (км) – проехали два автобуса; 450-300=150 (км) – осталось проехать.
Ответ: Через 2часа расстояние между автобусами будет 150 км.
Задачи на движение в противоположных направлениях
В таких задачах два объекта движутся в противоположных направлениях, отдаляясь друг от друга. В таком типе задачи используется скорость удаления. Задачи на движение в противоположных направлениях также можно решить двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость удаления объектов (как сумму их скоростей), общие время и расстояние. Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Задача 6.
Два автомобиля выехали одновременно из одного и того же пункта в противоположных направлениях. Скорость первого автомобиля 100 км/ч, скорость второго – 70 км/ч. Какое расстояние будет между автомобилями через 4 часа?
Решение:
Первый способ. Определить расстояние, которое проехал каждый автомобиль и найти сумму полученных результатов:
1) 100 · 4 = 400 (км) – проехал первый автомобиль
2) 70 · 4 = 280 (км) – проехал второй автомобиль
400 + 280 = 680 (км)
Второй способ. Найти скорость удаления, то есть значение увеличения расстояния между автомобилями за каждый час, а затем скорость удаления умножить на время в пути.
100 + 70= 170 км/ч – это скорость удаления автомобилей.
170 · 4 = 680 (км)
Ответ: Через 4 часа между автомобилями будет 680 км.
Задача 7.
Из двух населённых пунктов, расстояние между которыми 40 км, вышли в противоположных направлениях два туриста. Первый турист шёл со скоростью 4 км/ч, а второй — 5 км/ч. Какое расстояние между туристами будет через 5 часов?
Решение:
Первый способ. Определить сколько километров прошёл каждый из туристов за 5 часов, сложить полученные результаты, а затем к полученному расстоянию прибавить расстояние между населенными пунктами.
1) 4 · 5 = 20 (км) – прошёл первый турист;
2) 5 · 5 = 25 (км) – прошёл второй турист;
3) 20 + 25 = 45 (км);
4) 45 + 40 = 85 (км).
Второй способ. Найти скорость удаления пешеходов, затем найти пройденное расстояние, к полученному результату прибавить расстоянием между населёнными пунктами.
4 + 5 = 9 (км/ч);
9 · 5 = 45 (км);
45 + 40 = 85 (км);
Ответ: Через 5 часов расстояние между пешеходами будет 85 км.
Задачи на движение в одном направлении
В таких задачах два объекта движутся в одном направлении с разной скоростью, при этом они сближаются друг с другом или отдаляются друг от друга. Соответственно находится скорость сближения или скорость удаления объектов.
Формула нахождения скорости сближения или удаления двух объектов, которые движутся в одном направлении: из большей скорости вычесть меньшую.
Задача 8.
Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?,
Решение:
Задачу можно решить с помощью уравнения.
В этом случае скорость первого автомобиля 40 км/час, время в пути на 4 часа больше, чем время второго автомобиля (или t+4). Скорость второго автомобиля 60 км/час, время в пути – t. Расстояние оба автомобиля проехали одинаковое. Поэтому можно составить уравнение: 40*(t+4)=60*t. Отсюда получаем t=8 (часов) – время в пути второго автомобиля, за которое он догонит первый.
Решение задачи без использования уравнения.
Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалиться от города на: 40 · 4 = 160 (км).
Второй автомобиль движется быстрее первого, значит, каждый час расстояние между автомобилями будет сокращаться на разность их скоростей: 60 — 40 = 20 (км/ч) – это скорость сближения.
Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся: 160 : 20 = 8 (ч)
Ответ: Второй автомобиль догонит первый через 8 часов.
Задача 9.
Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?
Решение: Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов: 5 — 4 = 1 (км/ч).
Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого: 5 : 1 = 5 (ч)
Ответ: Через 5 часов второй пешеход догонит первого.
Задача 10.
Два автомобиля выехали одновременно из одного и того же пункта в одном направлении. Скорость первого автомобиля 80 км/ч, а скорость второго – 40 км/ч.
1) Чему равна скорость удаления между автомобилями?
2) Какое расстояние будет между автомобилями через 3 часа?
3) Через сколько часов расстояние между ними будет 200 км?
Решение:
1) 80 — 40 = 40 (км/ч) — скорость удаления автомобилей друг от друга.
2) 40 · 3 = 120 (км) – расстояние между ними через 3 часа./
3) 200 : 40 = 5 (ч) – время, через которое расстояние между автомобилями станет 200 км.
Ответ:
1) Скорость удаления между автомобилями равна 40 км/ч.
2) Через 3 часа между автомобилями будет 120 км.
3) Через 5 часов между автомобилями будет расстояние в 200 км.
Задачи на движение по реке
Рассмотрим задачи, в которых речь идёт о движении объекта по реке. Скорость любого объекта в стоячей воде называют собственной скоростью этого объекта.
Чтобы узнать скорость объекта, который движется по течению реки, надо к собственной скорости объекта прибавить скорость течения реки. Чтобы узнать скорость объекта, который движется против течения реки, надо из собственной скорости объекта вычесть скорость течения реки.
Задача 11.
Лодка движется по реке. За сколько часов она преодолеет расстояние 120 км, если ее собственная скорость 27 км/ч, а скорость течения реки 3 км/ч?
Решение:
1) лодка движется по течению реки.
27 + 3 = 30 (км/ч) – скорость лодки по течению реки.
120 : 30 = 4 (ч) – проплывет путь.
2) лодка движется против течения реки.
27 — 3 = 24 (км/ч) — скорость лодки против течения реки
120 : 24 = 5 (ч) – проплывет путь.
Ответ:
1) При движении по течению реки лодка потратит 4 часа на путь.
2) При движении против течения реки лодка потратит 5 часов на путь.
Итак, для решения задач на движение:
- Основная формула:S=ν*t;
- Нужно сделать чертеж, который поможет определить тип задачи.
- Все цифры нужно привести в единые единицы измерения: длина и время
Заключение.
Решая много задач по данной теме, ученик обязательно научится быстро ориентироваться в понятиях «скорость», «время» и «расстояние» и быстро решать задачи всех типов.
Весь курс начальной школы (за 1-4 классы) в краткой форме на сайте edu.intmag24.ru. С помощью курса можно быстро повторить основные моменты и правила по предметам: русский язык, математика, окружающий мир.
Для решения более сложных задач на движение посмотрите, как составлять схемы и таблицы данных для наглядного представления и структурирования данных.
