Второй закон ньютона формула как найти массу – Сайт, где вы сможете решить свои вопросы

Классическая механика
История…
Фундаментальные понятия Пространство Время Масса Скорость Сила Механическая работа Энергия Импульс
Формулировки Ньютоновская механика Лагранжева механика Гамильтонова механика Формализм Гамильтона — Якоби Уравнения Рауса Уравнения Аппеля Теория Купмана — фон Неймана
Разделы Прикладная механика Небесная механика Механика сплошных сред Геометрическая оптика Статистическая механика
Учёные Галилей Кеплер Ньютон Эйлер Лаплас Д’Аламбер Лагранж Гамильтон Коши
См. также: Портал:Физика

Второ́й зако́н Нью́то́на — дифференциальный закон механического движения, описывающий зависимость ускорения тела от равнодействующей всех приложенных к телу сил и массы тела. Один из трёх законов Ньютона. Основной закон динамики^[1]^[2]^[3].

Объектом, о котором идёт речь во втором законе Ньютона, является материальная точка, обладающая неотъемлемым свойством — инерцией^[4], величина которой характеризуется массой. В классической (ньютоновской) механике масса материальной точки полагается постоянной во времени и не зависящей от каких-либо особенностей её движения и взаимодействия с другими телами^[5]^[6]^[7]^[8].

Второй закон Ньютона в его наиболее распространённой формулировке, справедливой для скоростей, много меньших скорости света, утверждает: в инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, не зависит от её природы^[9], совпадает с ней по направлению и обратно пропорционально массе материальной точки^[10].

Второй закон Ньютона в классической механике[править | править код]

Возможные формулировки[править | править код]

В своём труде «Математические начала натуральной философии» Исаак Ньютон приводит следующую формулировку^[11] своего закона:

Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.

Современная формулировка:

В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.

Обычно этот закон записывается в виде формулы

${vec {a}}={frac {{vec {F}}}{m}},$

где ${vec {a}}$ — ускорение тела, $vec{F}$ — сила, приложенная к телу, а $m$ — масса тела.

Или в ином виде:

$m{vec {a}}={vec {F}}$

Формулировка второго закона Ньютона с использованием понятия импульса:

В инерциальных системах отсчёта производная импульса материальной точки по времени равна действующей на неё силе^[12]:

${frac {d{vec {p}}}{dt}}={vec {F}},$

где ${vec p}=m{vec v}$ — импульс (количество движения) точки, ${vec {v}}$ — её скорость, а $t$ — время.

Область применения закона[править | править код]

Второй закон Ньютона в классической механике сформулирован применительно к движению материальной точки. Предполагается, что масса материальной точки неизменна во времени^[13]^[14]^[15]. Уравнения, соответствующие данному закону, называются уравнениями движения материальной точки или основными уравнениями динамики материальной точки.

Иногда в рамках классической механики предпринимались попытки распространить сферу применения уравнения ${displaystyle d{vec {p}}/dt={vec {F}}}$ и на случай тел переменной массы. Однако вместе с таким расширительным толкованием уравнения приходилось существенным образом модифицировать принятые ранее определения и изменять смысл таких фундаментальных понятий, как материальная точка, импульс и сила^[16]^[17].

В случае, когда на материальную точку действует несколько сил, каждая из них сообщает точке ускорение, определяемое вторым законом Ньютона так, как если бы других сил не было (принцип суперпозиции сил). Поэтому результирующее ускорение материальной точки можно определить по второму закону Ньютона, подставив в него равнодействующую силу^[18].

Уравнение второго закона Ньютона ${displaystyle {vec {F}}=m{vec {a}}}$ предполагает скалярную аддитивность масс^[19].

Помимо материальной точки, уравнение второго закона Ньютона применимо также для описания механического движения центра масс механической системы. Центр масс движется, как материальная точка, имеющая массу, равную массе всей системы, и находящаяся под действием всех внешних сил, приложенных к точкам системы (теорема о движении центра масс системы).

Уравнение второго закона Ньютона может быть записано в виде ${displaystyle dmcdot d{vec {v}}/dt=d{vec {F}}}$ для распределённой силы, где ${displaystyle dm=rho dV}$ — элемент массы ( $rho$ — плотность вещества, $dV$ — элементарный объём), а ${displaystyle d{vec {F}}}$ — бесконечно малая действующая на него сила ( ${displaystyle {vec {f}}=d{vec {F}}/dV}$ — плотность силы). Отталкиваясь от такой записи, получают^[20] гидродинамический вариант закона — уравнение Эйлера.

Второй закон Ньютона выполняется только в инерциальных системах отсчёта^[21]^[22]. Тем не менее, добавляя к силам, действующим со стороны других тел, силы инерции, для описания движения в неинерциальных системах отсчёта можно пользоваться уравнением второго закона Ньютона^[23]. В таком случае для неинерциальной системы отсчёта уравнение движения записывается в той же форме, что и для инерциальной системы: масса тела, умноженная на его ускорение относительно неинерциальной системы отсчёта, равна по величине и направлению равнодействующей всех сил, включая и силы инерции, приложенные к телу^[24]^[25].

Логическая роль второго закона Ньютона[править | править код]

В ньютоновском изложении классической механики законы Ньютона ниоткуда не «выводятся», они имеют статус аксиом, базирующихся на совокупности экспериментальных фактов. Как и аксиомы математики, аксиомы ньютоновской динамики можно сформулировать немного по-разному.

При одном подходе второй закон Ньютона позиционируется как экспериментально проверяемое утверждение о пропорциональности ускорения вызывающей его силе и, одновременно, определение инертной массы тела через отношение величин силы и ускорения^[26]^[27]. Тогда основная идея второго закона состоит в декларации линейности соотношения «сила—ускорение», то есть что именно эти величины (а не, скажем, сила и скорость) и именно таким образом (а не квадратично и т. п.) связаны между собой.

При другом подходе можно ввести инертную массу независимо от второго закона Ньютона, через массу определённого тела, принимаемого за эталон. Тогда второй закон содержит два независимо экспериментально проверяемых утверждения: о пропорциональности ускорения силе и обратной пропорциональности массе^[28].

Во многих практических и учебных задачах второй закон Ньютона позволяет вычислять силу. Но данный закон не является дефиницией силы^[29] (высказывание типа «по определению, сила есть произведение массы на ускорение» неуместно), иначе он превратился бы в тавтологию.

В случае отсутствия воздействия на тело со стороны других тел ( ${displaystyle {vec {F}}=0}$ ), из второго закона Ньютона следует, что ускорение тела равно нулю. Отсюда может показаться, что первый закон Ньютона входит во второй как его частный случай. Однако, это не так, поскольку именно первым законом постулируется существование инерциальных систем отсчёта, что является самостоятельным содержательным утверждением. Соответственно, первый закон Ньютона формулируется независимо от второго^[30].

Второй закон Ньютона устанавливает связь между динамическими и кинематическими величинами^[31]. Кроме того, уравнение закона ${displaystyle {vec {F}}=m{vec {a}}}$ может рассматриваться как уравнение связи между физическими величинами при определении единиц силы в системах СИ, СГС и других^[32]. Единица силы определяется как такая сила, которая материальной точке с массой, равной единице массы, принимаемой в качестве основной, сообщает ускорение, равное единице ускорения, определённой ранее в качестве производной единицы^[33]. (При независимом выборе единиц массы, силы и ускорения выражение второго закона нужно писать в виде ${displaystyle m{vec {a}}=k{vec {F}}}$ , где $k$ — коэффициент пропорциональности, определяющийся выбором единиц измерения^[34]^[35]^[36]^[37]).

Сила $vec{F}$ во втором законе Ньютона зависит только от координат ${vec {r}}$ и скорости $vec{v}$ материальной точки: ${displaystyle {dot {vec {p}}}={vec {F}}({vec {r}},{vec {v}})}$ . Основная задача физической механики сводится к нахождению функции ${displaystyle {vec {F}}({vec {r}},{vec {v}})}$ ^[38].

Формула второго закона Ньютона ${displaystyle {vec {a}}={vec {F}}/m}$ выражает принцип причинности классической механики. Координаты и скорости материальной точки в момент времени ${displaystyle t+Delta t}$ (где $Delta tto 0$ ) непрерывно и однозначно определяются через их значения в момент времени $t$ и заданную силу $vec{F}$ , действующую на материальную точку. Разлагая в ряд Тейлора и ограничиваясь малыми первого порядка по $t$ , получаем^[39]: ${displaystyle {vec {r}}(t+Delta t)={vec {r}}(t)+{vec {v}}Delta t}$ , ${displaystyle {vec {v}}(t+Delta t)={vec {v}}(t)+{vec {a}}Delta t}$ . Форма, в которой в механике реализуется причинность, называется механистическим или лапласовским детерминизмом^[40].

Уравнение второго закона Ньютона ${displaystyle {vec {F}}=m{vec {a}}}$ инвариантно относительно преобразований Галилея. Это утверждение называется принципом относительности Галилея^[41].

В классической механике закон сохранения энергии, закон сохранения импульса и закон сохранения момента импульса являются следствиями второго закона Ньютона, однородности времени, однородности и изотропности пространства, а также некоторых предположений относительно характера действующих сил^[42].

В случае, когда сила $vec{F}$ постоянна, интегрирование уравнения второго закона Ньютона ${displaystyle {frac {d{vec {v}}}{dt}}={frac {vec {F}}{m}}}$ приводит к равенству ${displaystyle {vec {v}}_{2}-{vec {v}}_{1}={frac {vec {F}}{m}}(t_{2}-t_{1})}$ . Это соотношение показывает, что под действием заданной силы $vec{F}$ определённое изменение скорости ${displaystyle Delta {vec {v}}={vec {v}}_{2}-{vec {v}}_{1}}$ у тела с большей массой происходит за более продолжительный промежуток времени. Поэтому говорят, что все тела обладают инерцией, а массу $m$ называют мерой инерции тела^[43].

Запись закона в разных системах координат[править | править код]

Основной источник: ^[18]

Векторная запись второго закона Ньютона ${displaystyle m{vec {a}}={vec {F}}}$ верна для любой инерциальной системы координат, относительно которой определяются входящие в этот закон величины (сила, масса, ускорение)^[44]. Однако, разложение на компоненты (проекции) будет различным для декартовой, цилиндрической и сферической систем. Интерес также представляет разложение на нормальную и тангенциальную составляющие.

Декартова прямоугольная система координат

${displaystyle m{ddot {x}}=F_{x}}$ , ${displaystyle m{ddot {y}}=F_{y}}$ , ${displaystyle m{ddot {z}}=F_{z}}$ ,
где ${displaystyle {vec {F}}=F_{x}{vec {i}}+F_{y}{vec {j}}+F_{z}{vec {k}}}$ , а орты декартовой системы $vec{i}$ , $vec{j}$ , $vec{k}$ направлены по осям координат (в сторону возрастания конкретной координаты),

Цилиндрическая система координат

${displaystyle m({ddot {rho }}-rho {dot {varphi }}^{2})=F_{rho }}$ , ${displaystyle m(rho {ddot {varphi }}+2{dot {rho }}{dot {varphi }})=F_{varphi }}$ , ${displaystyle m{ddot {z}}=F_{z}}$ ,
где ${displaystyle {vec {F}}=F_{rho }{vec {e}}_{rho }+F_{varphi }{vec {e}}_{varphi }+F_{z}{vec {e}}_{z}}$ , а орты ${displaystyle {vec {e}}_{rho }}$ , ${displaystyle {vec {e}}_{varphi }}$ , ${displaystyle {vec {e}}_{z}}$ цилиндрической системы берутся в точке приложения силы и направлены, соответственно, от оси $z$ под 90⁰ к ней, по окружности в плоскости $xy$ с центром на оси, и вдоль $z$ (в сторону возрастания конкретной координаты),

Сферическая система координат

${displaystyle m({ddot {r}}-r{dot {varphi }}^{2}sin ^{2}theta -r{dot {theta }}^{2})=F_{r}}$ ,
${displaystyle m([r{ddot {varphi }}+2{dot {r}}{dot {varphi }}]sin theta +2r{dot {varphi }}{dot {theta }}cos theta )=F_{varphi }}$ ,
${displaystyle m(2{dot {r}}{dot {theta }}+r{ddot {theta }}-r{dot {varphi }}^{2}sin theta cos theta )=F_{theta }}$ ,
где ${displaystyle {vec {F}}=F_{r}{vec {e}}_{r}+F_{varphi }{vec {e}}_{varphi }+F_{theta }{vec {e}}_{theta }}$ , а орты ${displaystyle {vec {e}}_{r}}$ , ${displaystyle {vec {e}}_{varphi }}$ , ${displaystyle {vec {e}}_{theta }}$ сферической системы берутся в точке приложения силы и направлены, соответственно, от центра $O$ , по «параллелям», и по «меридианам» (в сторону возрастания конкретной координаты).

Разложение в соприкасающейся плоскости

В соприкасающейся плоскости ускорение ${displaystyle {vec {a}}={vec {a}}_{n}+{vec {a}}_{tau }}$ материальной точки массой $m$ и действующую на неё силу ${displaystyle {vec {F}}={vec {F}}_{n}+{vec {F}}_{tau }}$ можно разложить на нормальную (перпендикулярную касательной к траектории в соприкасающейся плоскости) ${displaystyle {vec {F}}_{n}=m{vec {a}}_{n}}$ и тангенциальную (параллельную касательной к траектории в соприкасающейся плоскости) ${displaystyle {vec {F}}_{tau }=m{vec {a}}_{tau }}$ составляющие.

Абсолютная величина нормальной силы равна ${displaystyle F_{n}=ma_{n}=mv^{2}/R}$ , где $R$ — радиус кривизны траектории материальной точки, $v$ — абсолютная величина её скорости. Нормальная сила направлена к центру кривизны траектории материальной точки. В случае круговой траектории радиуса $R$ абсолютная величина нормальной силы ${displaystyle F_{n}=momega ^{2}R}$ , где $omega$ — угловая скорость обращения точки. Нормальную силу также называют центростремительной.

Тангенциальная составляющая силы равна ${displaystyle F_{tau }=ma_{tau }=m{frac {d^{2}s}{dt^{2}}}}$ , где ${displaystyle s=s(t)}$ — дуговая координата по траектории точки^[45]. Если ${displaystyle {frac {d^{2}s}{dt^{2}}}>0}$ , то сила ${displaystyle {vec {F}}_{tau }}$ совпадает по направлению с вектором скорости $vec{v}$ и её называют движущей силой. Если ${displaystyle {frac {d^{2}s}{dt^{2}}}<0}$ , то сила ${displaystyle {vec {F}}_{tau }}$ противоположна по направлению вектору скорости $vec{v}$ и её называют тормозящей силой.

Второй закон за пределами классической механики[править | править код]

В релятивистской динамике[править | править код]

Второй закон Ньютона в виде $m{vec {a}}={vec {F}}$ приближённо справедлив только для скоростей, много меньших скорости света, и в инерциальных системах отсчёта.

В виде ${frac {d{vec {p}}}{dt}}={vec {F}}$ второй закон Ньютона точно справедлив также в инерциальных системах отсчёта специальной теории относительности и в локально инерциальных системах отсчёта общей теории относительности, однако при этом вместо прежнего выражения для импульса используется равенство ${vec p}={frac {m{vec v}}{{sqrt {1-{frac {displaystyle v^{2}}{displaystyle c^{2}}}}}}}$ , где $c$ — скорость света^[46].

Существует и четырёхмерное релятивистское обобщение второго закона Ньютона. Производная четырёхимпульса ${displaystyle {vec {mathrm {P} }}}$ по собственному времени $tau$ материальной точки равна четырёхсиле ${displaystyle {vec {Phi }}}$ ^[47]:

${displaystyle {vec {Phi }}={frac {d{vec {mathrm {P} }}}{dtau }}}$ .

В релятивистской динамике вектор трёхмерного ускорения ${vec {a}}$ уже не параллелен вектору трёхмерной силы $vec{F}$ ^[48].

В квантовой механике[править | править код]

Законы ньютоновской динамики, в том числе второй закон Ньютона, неприменимы, если длина волны де Бройля рассматриваемого объекта соизмерима с характерными размерами области, в которой изучается его движение. В этом случае необходимо пользоваться квантовомеханическими законами^[49].

Тем не менее, второй закон Ньютона при определённых условиях актуален применительно к движению волнового пакета в квантовой механике. Если потенциальная энергия волнового пакета пренебрежимо мало изменяется в области нахождения пакета, то производная по времени среднего значения импульса пакета будет равна силе, понимаемой как градиент потенциальной энергии, взятый с обратным знаком (теорема Эренфеста).

Для описания движения частицы в потенциальном поле, в квантовой механике справедливо операторное уравнение, по форме совпадающее с уравнением второго закона Ньютона: ${displaystyle m{frac {d{hat {v}}}{dt}}=-nabla {hat {U}}}$ . Здесь: $m$ — масса частицы, ${displaystyle {hat {v}}={frac {hat {p}}{m}}}$ — оператор скорости, ${hat {p}}$ — оператор импульса, ${displaystyle {hat {U}}=U(x,y,z)}$ — оператор потенциальной энергии^[50].

Видоизменённый второй закон Ньютона используется и при квантовомеханическом описании движения электронов в кристаллической решётке. Взаимодействие электрона с периодическим электромагнитным полем решётки при этом учитывается введением понятия эффективной массы.

Научно-историческое значение закона[править | править код]

Оценивая значение второго закона Ньютона, А. Эйнштейн писал:

Дифференциальный закон является той единственной формой причинного объяснения, которая может полностью удовлетворять современного физика. Ясное понимание дифференциального закона есть одно из величайших духовных достижений Ньютона… Только переход к рассмотрению явления за бесконечно малое время (т. е. к дифференциальному закону) позволил Ньютону дать формулировку, пригодную для описания любого движения… Так Ньютон пришёл… к установлению знаменитого закона движения:

Вектор ускорения × Масса = Вектор силы.

Это — фундамент всей механики и, пожалуй, всей теоретической физики.

— Эйнштейн А. Собрание научных трудов. — М.: Наука, 1967. — Т. 4. — С. 82, 92. — 599 с. — 31 700 экз.

Все законы природы для сил в зависимости от свойств тел, их состояний и движений получаются из опытов и устанавливаются всегда и только на основе решения уравнения ${displaystyle {vec {F}}=m{vec {a}}}$ , которое употребляется для выражения силы^[51].

Второй закон Ньютона является важной частью парадигмы, принятой в классической физической картине мира^[52].

Лагранжево и гамильтоново обобщения закона[править | править код]

В аналитической механике существует два аксиоматических подхода. При одном подходе в качестве аксиомы принимается второй закон Ньютона и из него выводятся уравнения Лагранжа. При другом подходе в качестве аксиомы принимаются уравнения Лагранжа. Тогда второй закон Ньютона рассматривается как следствие из них ^[53].

Из уравнений Лагранжа для произвольной голономной системы, на которую действуют как потенциальные ( ${displaystyle Q_{i}^{p}}$ ), так и непотенциальные ( ${displaystyle Q_{i}^{n}}$ ) обобщённые силы, ${displaystyle {frac {d}{dt}}left({frac {partial L}{partial {dot {q}}_{i}}}right)-{frac {partial L}{partial q_{i}}}=Q_{i}^{n}}$ следует, что производная по времени обобщённого импульса ${displaystyle p_{i}={frac {partial L}{partial {dot {q}}_{i}}}}$ равна суммарной обобщённой силе ${displaystyle Q_{i}=Q_{i}^{p}+Q_{i}^{n}={frac {partial L}{partial q_{i}}}+Q_{i}^{n}}$ :

${displaystyle {dot {p}}_{i}=Q_{i}}$ .

Записанные так в декартовых координатах уравнения Лагранжа называются уравнениями движения в форме Ньютона^[54].

Теорема об изменении обобщённого импульса обобщает и включает как частные случаи теоремы ньютоновской динамики об изменении количества движения и об изменении кинетического момента^[55].

В гамильтоновой динамике

${displaystyle {dot {p}}_{i}=-{frac {partial H}{partial q_{i}}}}$ ,

где, как и выше, ${displaystyle p_{i}={frac {partial L}{partial {dot {q}}_{i}}}}$ — обобщённый импульс, через ${displaystyle H=sum _{i=1}^{s}p_{i}{dot {q}}_{i}-L}$ обозначена функция Гамильтона, а ${displaystyle L=L(q_{i},{dot {q}}_{i},t)}$ — лагранжиан, то есть разность кинетической и потенциальной энергий системы.

См. также[править | править код]

Первый закон Ньютона
Уравнение Гейзенберга
Уравнение Мещерского
Уравнение Эренфеста
Теорема о движении центра масс системы
Принцип причинности

Примечания[править | править код]

↑ Г. А. Бугаенко, В. В. Маланин, В. И. Яковлев Основы классической механики. — М., Высшая школа, 1999. — ISBN 5-06-003587-5 — Тираж 3000 экз. — c. 43
↑ Кузнецов Б. Г. Основные принципы физики Ньютона // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — Тираж 5000 экз. — с. 188;
↑ Тарасов В. Н., Бояркина И. В., Коваленко М. В., Федорченко Н. П., Фисенко Н. И. Теоретическая механика. — М., ТрансЛит, 2012. — ISBN 978-5-94976-455-8. — Тираж 1000 экз. — с. 249
↑ То же, что инертность. См. Инерция // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2: Добротность — Магнитооптика. — С. 146. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
↑ “Дополнительной характеристикой (по сравнению с геометрическими характеристиками) материальной точки является скалярная величина m — масса материальной точки, которая, вообще говоря, может быть как постоянной, так и переменной величиной. … В классической ньютоновской механике материальная точка обычно моделируется геометрической точкой с присущей ей постоянной массой) являющейся мерой её инерции.” стр. 137 Седов Л. И., Цыпкин А. Г. Основы макроскопических теорий гравитации и электромагнетизма. М: Наука, 1989.
↑ Маркеев А. П. Теоретическая механика. — М.: ЧеРО, 1999. — С. 87. — 572 с. «Масса материальной точки считается постоянной величиной, не зависящей от обстоятельств движения».
↑ Голубев Ю. Ф. Основы теоретической механики. — М.: МГУ, 2000. — С. 160. — 720 с. — ISBN 5-211-04244-1. «Аксиома 3.3.1. Масса материальной точки сохраняет своё значение не только во времени, но и при любых взаимодействиях материальной точки с другими материальными точками независимо от их числа и от природы взаимодействий».
↑ Тарг С. М. Краткий курс теоретической механики. — М.: Высшая школа, 1995. — С. 287. — 416 с. — ISBN 5-06-003117-9. «В классической механике масса каждой точки или частицы системы считается при движении величиной постоянной»
↑ Бутиков Е.И., Быков А.А., Кондратьев А.С. Физика для поступающих в вузы. — М.: Наука, 1982. — С.39.
↑ Ландсберг Г. С. Элементарный учебник физики. Том 1. Механика. Теплота. Молекулярная физика. — М.: Наука, 1975. — C. 107
↑ Исаак Ньютон. Математические начала натуральной философии. — М.: Наука, 1989. — С. 40. — 690 с. — («Классики науки»). — 5000 экз. — ISBN 5-02-000747-1.
↑ Сивухин Д. В. Общий курс физики. — М.: Физматлит; изд-во МФТИ, 2005. — Т. I. Механика. — С. 76. — 560 с. — ISBN 5-9221-0225-7.
↑ Маркеев А. П. Теоретическая механика. — М.: ЧеРО, 1999. — С. 254. — 572 с. «…второй закон Ньютона справедлив только для точки постоянного состава. Динамика систем переменного состава требует особого рассмотрения».
↑ Иродов И. Е. Основные законы механики. — М.: Высшая школа, 1985. — С. 41. — 248 с.«В ньютоновской механике… m=const и dp/dt=ma».
↑ Kleppner D., Kolenkow R. J. An Introduction to Mechanics. — McGraw-Hill, 1973. — P. 112. — ISBN 0-07-035048-5. Архивная копия от 17 июня 2013 на Wayback Machine Архивированная копия. Дата обращения: 9 февраля 2013. Архивировано из оригинала 17 июня 2013 года. «For a particle in Newtonian mechanics, M is a constant and (d/dt)(Mv) = M(dv/dt) = Ma».
↑ Зоммерфельд А. Механика = Sommerfeld A. Mechanik. Zweite, revidierte Auflage, 1944. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 45-46. — 368 с. — ISBN 5-93972-051-X.
↑ Кильчевский Н. А. Курс теоретической механики. Том 1. — М.: Наука, 1977. 480 с.
↑ ¹ ² Яворский Б.М., Детлаф А.А., Лебедев А.К. Справочник по физике для инженеров и студентов вузов. — М.: Оникс, 2007. — ISBN 978-5-488-01248-6. — Тираж 5 100 экз. — С. 38 – 39
↑ Орир Дж. Физика // М., Мир, 1981. — Тираж 75 000 экз. — Том 1. — с. 54
↑ Д. В. Александров, А. Ю. Зубарев, Л. Ю. Искакова. Введение в гидродинамику. Изд-во УрФУ, Екатеринбург (2012). — см. стр. 8-11. Дата обращения: 30 апреля 2023.
↑ Савельев И. В. Курс общей физики. Том 1. Механика. Молекулярная физика. — М.: Наука, 1987. — C. 118
↑ Ландсберг Г. С. Элементарный учебник физики. Том 1. Механика. Теплота. Молекулярная физика. — М.: Наука, 1975. — C. 289
↑ Савельев И. В. Курс общей физики. Том 1. Механика. Молекулярная физика. — М.: Наука, 1987. — C. 118-119
↑ Ландсберг Г. С. Элементарный учебник физики. Том 1. Механика. Теплота. Молекулярная физика. — М.: Наука, 1975. — C. 291
↑ Савельев И. В. Курс общей физики. Том 1. Механика. Молекулярная физика. — М.: Наука, 1987. — C. 119
↑ Ландсберг Г. С. Элементарный учебник физики. Том 1. Механика. Теплота. Молекулярная физика. — М.: Наука, 1975. — C. 106
↑ Хайкин С. Э. Физические основы механики. — М.: Физматгиз, 1963. — C. 104
↑ Бутиков Е.И., Быков А.А., Кондратьев А.С. Физика для поступающих в вузы. — М.: Наука, 1982. — С. 30.
↑ Р. Ф. Фейнман Фейнмановские лекции по физике. Том I. Современная наука о природе Законы механики. — М.: Наука, 1978. — С. 209-210.
↑ Савельев И. В. Курс общей физики. Том 1. Механика. Молекулярная физика. — М.: Наука, 1987. — C. 54
↑ Селезнев Ю. А. Основы элементарной физики. – М., Наука, 1966. – Тираж 100 000 экз. – с. 40
↑ Г. Д. Бурдун, Б. Н. Марков Основы метрологии. — М.: Издательство стандартов, 1972. — Тираж 30 000 экз. — С. 49.
↑ Сена Л. А. Единицы физических величин и их размерности. — М.: Наука, 1977. — С. 24.
↑ Савельев И. В. Курс общей физики / 2-е изд., перераб. — М.: Наука, 1982. — Т. 1. Механика. Молекулярная физика. — С. 54. — 432 с. Архивная копия от 4 февраля 2014 на Wayback Machine
↑ Сена Л. А. Единицы физических величин и их размерности. — М.: Наука, 1969. — С. 22. — 304 с. Архивная копия от 1 февраля 2014 на Wayback Machine
↑ Мултановский В.В. Курс теоретической физики: Классическая механика. Основы специальной теории относительности. Релятивистская механика. — М.: Просвещение, 1988. — С. 73. — 304 с. — ISBN 5-09-000625-3. Архивная копия от 5 июля 2014 на Wayback Machine
↑ «Не следует смешивать понятия силы и произведения массы на ускорение, которому она равна» (Фок В.А. Механика. Рецензия на книгу: Л. Ландау и Л. Пятигорский. Механика. (Теоретическая физика под общей редакцией проф. Л.Д. Ландау, т. I). Гостехиздат. Москва — Ленинград, 1940 // УФН. — 1946. — Т. 28, вып. 2–3. — С. 377–383. Архивировано 31 октября 2015 года.).
↑ Сивухин Д. В. Общий курс физики. Механика. – М., Наука, 1979. – Тираж 50 000 экз. – с. 71-72
↑ Р. Ф. Фейнман Фейнмановские лекции по физике. Том I. Современная наука о природе Законы механики. — М.: Наука, 1978. — С. 164.
↑ Бугаенко Г. А., Маланин В. В., Яковлев В. И. Основы классической механики. — М.: Высшая школа, 1999. ISBN 5-06-003587-5 — Тираж 3 000 экз. — С. 47.
↑ Сивухин Д. В. Общий курс физики. Механика. – М., Наука, 1979. – Тираж 50 000 экз. – с. 94
↑ Сивухин Д. В. Общий курс физики. Механика. – М., Наука, 1979. – Тираж 50 000 экз. – с. 199
↑ Жирнов Н. И. Классическая механика. – М., Просвещение, 1980. – с. 34-35
↑ Р. Неванлинна Пространство, время и относительность. – М., Мир, 1966. – c. 202
↑ Тарасов В. Н., Бояркина И. В., Коваленко М. В. Теоретическая механика. – М., ТрансЛит, 2012. – ISBN 978-5-94976-455-8. – с. 254
↑ Савельев И. В. Курс общей физики. Т. 1. Механика. Молекулярная физика.
— М.: Наука, 1987. — С. 237.
↑ Бугаенко Г. А., Маланин В. В., Яковлев В. И. Основы классической механики. — М.: Высшая школа, 1999. — С. 347. — ISBN 5-06-003587-5
↑ Кычкин И. С., Сивцев В. И. Школьная физика: второй закон Ньютона Архивная копия от 30 мая 2019 на Wayback Machine // Международный журнал экспериментального образования. – 2016. № 3-2. – С. 194-197.
↑ Бутиков Е. И., Быков А. А., Кондратьев А. С. Физика для поступающих в вузы. — М.: Наука, 1982. — С. 544.
↑ Ландау Л. Д., Лившиц Е. М. Квантовая механика. — М., Наука, 1972. — с. 76
↑ Седов Л.И.Методы подобия и размерности в механике. — М.: Гостехтеориздат, 1954. — С. 21 – 28.
↑ Томас Кун Структура научных революций. — М., АСТ, 2020. — ISBN 978-5-17-122824-8. — с. 280-282
↑ Айзерман М.А. Классическая механика. — М.: Наука, 1980. — Тираж 17 500 экз. — С. 164-165
↑ Медведев Б. В. Начала теоретической физики. Механика, теория поля, элементы квантовой механики. — М.: Физматлит, 2007. — ISBN 978-5-9221-0770-9 — С. 38.
↑ Бугаенко Г. А., Маланин В. В., Яковлев В. И. Основы классической механики. — М.: Высшая школа, 1999. — С. 247. — ISBN 5-06-003587-5

Ссылки[править | править код]

Gundlach J. H., Schlamminger S., Spitzer C. D., Choi K.-Y., Woodahl B. A., Coy J. J., Fischbach E. Laboratory Test of Newton’s Second Law for Small Accelerations (англ.). Phys. Rev. Lett., Vol. 98. American Physical Society (13 апреля 2007). Дата обращения: 7 апреля 2017. Архивировано 30 марта 2021 года.

Источник

Определение 1

Второй закон Ньютона представляет собой основной закон динамики. Данный закон может выполняться только в инерциальных системах отсчета.

Формулируя второй закон, стоит обратить внимание на то, что в динамике вводятся масса тела m и сила F→, а также способы их измерения. Масса является количественной характеристикой инертных свойств тела и показывает реакцию тела на внешнее воздействие. Сила же F→ представляет из себя количественную меру действия одного объекта на другой.

2-ой закон Ньютона, определение и формула

Второй закон Ньютона – фундаментальный закон природы, являющийся обобщением опытных фактов, подразделяющихся на две категории:

Если на обладающие разной массой тела подействовать одной и той же силой, то приобретаемые телами ускорения окажутся обратно пропорциональны их массам:

a~1m, при F=const.

Если силами различной величины подействовать на одно тело, то ускорения тела окажутся прямо пропорциональными приложенным силам:

a→~F→, при m=const.

Основной закон динамики был сформулирован Ньютоном путем обобщения данных фактов:

Определение 2

Сила, которая оказывает воздействие на тело, эквивалентна произведению массы тела на сообщаемое данной силой ускорение:

F→=ma→.

Приведенное выражение и представляет собой второй закон Ньютона.

С помощью него стало возможным вычисление ускорение тела в случае, если известна его масса m и действующая на него сила F→:

a→=F’m.

Определение 3

В Международной системе единиц (СИ) в качестве единицы силы считают такую силу, которая сообщающая телу массой 1 кг ускорение 1 м/с2. Данная единица называется ньютоном (Н). В (СИ) ее принимают за эталон силы.

1 Н=1кг·мс2.

Равнодействующая сила

В том случае, если на тело одновременно воздействуют несколько сил, как например, F1→, F2→ и F3→, то силой F→ в формуле второго закона Ньютона считается равнодействующая всех сил это величина, выражающаяся в виде формулы:

F→=F1→+F2→+F3→.

Равнодействующая сила

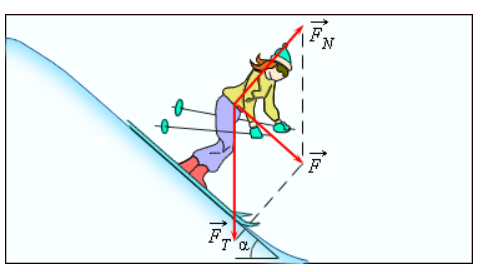
Рисунок 1.8.1. Сила F→ – равнодействующая силы тяжести F→Т и силы нормального давления FN→, действующих на лыжницу на гладкой горе. Сила F→ вызывает ускорение лыжника.

В случае же, когда равнодействующая сила F→=0, тело будет пребывать в состоянии покоя или равномерного прямолинейного движения. Выходит, что формально второй закон Ньютона включает в себя в качестве частного случая первый закон Ньютона. Но первый закон Ньютона обладает более глубоким физическим значением. Он обуславливает существование инерциальных систем отсчета.

Равнодействующая сила

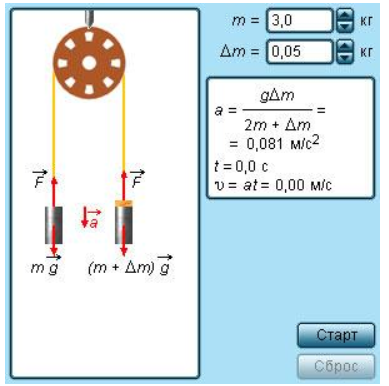
Рисунок 1.8.1. Модель движения тел на легком блоке.

Источник

Ответы Mail.ru

Домашние задания

Русский язык
Литература
Математика
Алгебра
Геометрия
Иностранные языки
Химия
Физика
Биология
История
Обществознание
География
Информатика
Экономика

Другие предметы

Вопросы – лидеры.

Помогите пожалуйста! СРОЧНО!!!!!
Сделайте развёрнуто и кратко.

1 ставка

Решите пожалуйста задачу

1 ставка

Просьба оказать помощь в решении задачи

1 ставка

Помогите пожалуйста,очень срочно нужно выполнить

1 ставка

Лидеры категории

Лена-пена

Искусственный Интеллект

М.И.

Искусственный Интеллект

Y.Nine

Искусственный Интеллект

king71alex
Куклин Андрей
Gentleman
Dmitriy
•••

Joker

Мастер

(1206),
закрыт

13 лет назад

Лучший ответ

-=[0][0][7]=-

Ученик

(176)

13 лет назад

m=F/a

Остальные ответы

Анютка Рычкова

Мудрец

(15419)

13 лет назад

нужно F разделить на а

Регина Исмагилова

Знаток

(275)

13 лет назад

m=F/a

Алексей Спицын

Ученик

(125)

13 лет назад

m=F/a

Артур Просто

Знаток

(331)

13 лет назад

надо F разделить на а… это точно

Владимир

Просветленный

(24392)

13 лет назад

да ребята я в ахе с ВАС…. фэ дели на а

Андрей Рязанцев

Профи

(740)

13 лет назад

Вы что прикалываетесь, или нечего делать? Ну такие действия должен делать первокласник. А второй закон учится наверное в 8 кл. Вот и делайте выводы

Стальной

Мастер

(1363)

13 лет назад

m=F/a

Похожие вопросы

Источник

Мы уже говорили об основах классической механики. Настала пора поговорить о них подробнее и затронуть в обсуждении чуть больше, чем просто основу. В этой статье мы подробно разберем основные законы классической механики. Как вы уже догадались, речь пойдет о законах Ньютона.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Основные законы классической механики Исаак Ньютон (1642-1727) собрал и опубликовал в 1687 году. Три знаменитых закона были включены в труд, который назывался «Математические начала натуральной философии».

Был долго этот мир глубокой тьмой окутан
Да будет свет, и тут явился Ньютон.

(Эпиграмма 18-го века)

Но сатана недолго ждал реванша –
Пришел Эйнштейн, и стало все как раньше.

(Эпиграмма 20-го века)

Что стало, когда пришел Эйнштейн, читайте в отдельном материале про релятивистскую динамику. А мы пока приведем формулировки и примеры решения задач на каждый закон Ньютона.

Первый закон Ньютона

Первый закон Ньютона гласит:

Существуют такие системы отсчета, называемые инерциальными, в которых тела движутся равномерно и прямолинейно, если на них не действуют никакие силы или действие других сил скомпенсировано.

Проще говоря, суть первого закона Ньютона можно сформулировать так: если мы на абсолютно ровной дороге толкнем тележку и представим, что можно пренебречь силами трения колес и сопротивления воздуха, то она будет катиться с одинаковой скоростью бесконечно долго.

Инерция – это способность тела сохранять скорость как по направлению, так и по величине, при отсутствии воздействий на тело. Первый закон Ньютона еще называют законом инерции.

До Ньютона закон инерции был сформулирован в менее четкой форме Галилео Галилеем. Инерцию ученый называл «неистребимо запечатленным движением». Закон инерции Галилея гласит: при отсутствии внешних сил тело либо покоится, либо движется равномерно. Огромная заслуга Ньютона в том, что он сумел объединить принцип относительности Галилея, собственные труды и работы других ученых в своих “Математических началах натуральной философии”.

Понятно, что таких систем, где тележку толкнули, а она покатилась без действия внешних сил, на самом деле не бывает. На тела всегда действуют силы, причем скомпенсировать действие этих сил полностью практически невозможно.

Например, все на Земле находится в постоянном поле силы тяжести. Когда мы передвигаемся (не важно, ходим пешком, ездим на машине или велосипеде), нам нужно преодолевать множество сил: силу трения качения и силу трения скольжения, силу тяжести, силу Кориолиса.

Инерция - способность тела продолжать движение

Второй закон Ньютона

Помните пример про тележку? В этот момент мы приложили к ней силу! Интуитивно понятно, что тележка покатится и вскоре остановится. Это значит, ее скорость изменится.

В реальном мире скорость тела чаще всего изменяется, а не остается постоянной. Другими словами, тело движется с ускорением. Если скорость нарастает или убывает равномерно, то говорят, что движение равноускоренное.

Если рояль падает с крыши дома вниз, то он движется равноускоренно под действием постоянного ускорения свободного падения g. Причем любой дугой предмет, выброшенный из окна на нашей планете, будет двигаться с тем же ускорением свободного падения.

Второй закон Ньютона устанавливает связь между массой, ускорением и силой, действующей на тело. Приведем формулировку второго закона Ньютона:

Ускорение тела (материальной точки) в инерциальной системе отсчета прямо пропорционально приложенной к нему силе и обратно пропорционально массе.

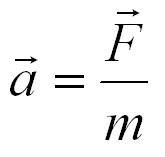
второй закон ньютона сила

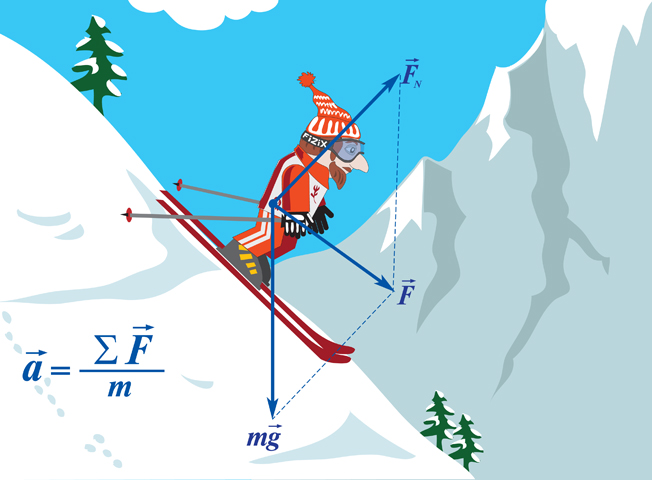
Рисунок - второй закон Ньютона

Если на тело действует сразу несколько сил, то в данную формулу подставляется равнодействующая всех сил, то есть их векторная сумма.

В такой формулировке второй закон Ньютона применим только для движения со скоростью, много меньшей, чем скорость света.

Существует более универсальная формулировка данного закона, так называемый дифференциальный вид.

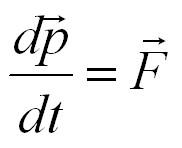
второй закон ньютона сила

В любой бесконечно малый промежуток времени dt сила, действующая на тело, равна производной импульса тела по времени.

Третий закон Ньютона

В чем состоит третий закон Ньютона? Этот закон описывает взаимодействие тел.

3 закон Ньютона говорит нам о том, что на любое действие найдется противодействие. Причем, в прямом смысле:

Два тела воздействуют друг на друга с силами, противоположными по направлению, но равными по модулю.

Формула, выражающая третий закон Ньютона:

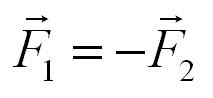
третий закон движения ньютона

Другими словами, третий закон Ньютона – это закон действия и противодействия.

Третий закон Ньютона

Пример задачи на законы Ньютона

Вот типичная задачка на применение законов Ньютона. В ее решении используются первый и второй законы Ньютона.

Десантник раскрыл парашют и опускается вниз с постоянной скоростью. Какова сила сопротивления воздуха? Масса десантника – 100 килограмм.

Решение:

Движение парашютиста – равномерное и прямолинейное, поэтому, по первому закону Ньютона, действие сил на него скомпенсировано.

На десантника действуют сила тяжести и сила сопротивления воздуха. Силы направлены в противоположные стороны.

По второму закону Ньютона, сила тяжести равна ускорению свободного падения, умноженному на массу десантника.

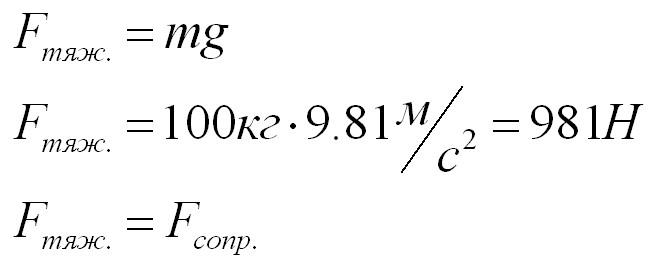
задача на законы Ньютона

Ответ: Сила сопротивления воздуха равна силе тяжести по модулю и противоположна направлена.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

А вот еще одна физическая задачка на понимание действия третьего закона Ньютона.

Комар ударяется о лобовое стекло автомобиля. Сравните силы, действующие на автомобиль и комара.

Решение:

По третьему закону Ньютона, силы, с которыми тела действуют друг на друга, равны по модулю и противоположны по направлению. Сила, с которой комар действует на автомобиль, равна силе, с которой автомобиль действует на комара.

Другое дело, что действие этих сил на тела сильно отличаются вследствие различия масс и ускорений.

Исаак Ньютон: мифы и факты из жизни

На момент публикации своего основного труда Ньютону было 45 лет. За свою долгую жизнь ученый внес огромный вклад в науку, заложив фундамент современной физики и определив ее развитие на годы вперед.

Он занимался не только механикой, но и оптикой, химией и другими науками, неплохо рисовал и писал стихи. Неудивительно, что личность Ньютона окружена множеством легенд.

Ниже приведены некоторые факты и мифы из жизни И. Ньютона. Сразу уточним, что миф – это не достоверная информация. Однако мы допускаем, что мифы и легенды не появляются сами по себе и что-то из перечисленного вполне может оказаться правдой.

Факт. Исаак Ньютон был очень скромным и застенчивым человеком. Он увековечил себя благодаря своим открытиям, однако сам никогда не стремился к славе и даже пытался ее избежать.
Миф. Существует легенда, согласно которой Ньютона осенило, когда на наго в саду упало яблоко. Это было время чумной эпидемии (1665-1667), и ученый был вынужден покинуть Кембридж, где постоянно трудился. Точно неизвестно, действительно ли падение яблока было таким роковым для науки событием, так как первые упоминания об этом появляются только в биографиях ученого уже после его смерти, а данные разных биографов расходятся.
Факт. Ньютон учился, а потом много работал в Кембридже. По долгу службы ему нужно было несколько часов в неделю вести занятия у студентов. Несмотря на признанные заслуги ученого, занятия Ньютона посещались плохо. Бывало, что на его лекции вообще никто не приходил. Скорее всего, это связано с тем, что ученый был полностью поглощен своими собственными исследованиями.
Миф. В 1689 году Ньютон был избран членом Кембриджского парламента. Согласно легенде, более чем за год заседания в парламенте вечно поглощенный своими мыслями ученый взял слово для выступления всего один раз. Он попросил закрыть окно, так как был сквозняк.
Факт. Неизвестно, как бы сложилась судьба ученого и всей современной науки, если бы он послушался матери и начал заниматься хозяйством на семейной ферме. Только благодаря уговорам учителей и своего дяди юный Исаак отправился учиться дальше вместо того, чтобы сажать свеклу, разбрасывать по полям навоз и по вечерам выпивать в местных пабах.

Дорогие друзья, помните – любую задачу можно решить! Если у вас возникли проблемы с решением задачи по физике, посмотрите на основные физические формулы. Возможно, ответ перед глазами, и его нужно просто рассмотреть. Ну а если времени на самостоятельные занятия совершенно нет, специализированный студенческий сервис всегда к вашим услугам!

В самом конце предлагаем посмотреть видеоурок на тему “Законы Ньютона”.

Источник

Второй закон Ньютона это закон который был выведен в результате проведения опытов Ньютоном.

В результате чего были выведена новая формула второго закона ньютона а = F /m,

Что такое второй закон Ньютона, масса и вес тела

Второй закон Ньютона Обобщая результаты опытов Галилея по падению тяжелых тел, астрономические законы Кеплера о движении планет, данные собственных исследований.

Ньютон сформулировал второй закон динамики, количественно связывающий изменение движения тела с силами, вызывающими это изменение.

Чтобы исследовать зависимость между силой и ускорением количественно, рассмотрим некоторые опыты.

Ускорение от величины силы

I. Рассмотрим, как зависит ускорение одного и того же тела от величины силы, действующей на это тело. Предположим, что к тележке прикреплен динамометр, по показаниям которого измеряют силу.

Измерив длину пройденного тележкой пути за какой-нибудь промежуток времени t, по формуле s = (at₂) : 2 определим ускорение a.

Изменяя величину силы, проделаем опыт несколько раз. Результаты измерения покажут, что ускорение прямо пропорционально силе, действующей на тележку

a₁ : a₂ = F₁ : F₂

ИЛИ

а ~ F.

Отношение силы, действующей на тело, к ускорению есть величина постоянная, которую обозначим m. Это отношение назовем массой тела.

Зависимость ускорения от массы

II. Установим зависимость ускорения тела от его массы. Для этого будем действовать на тележку какой-нибудь постоянной силой, изменяя массу (помещая различные грузы на тележку).

Ускорения тележки будем определять так же, как и в первом опыте. Опыт покажет, что ускорение тележки обратно пропорционально массе, то есть

(a₁/a₂) = (m₂/m₁), или а ~ (1/m)

Обобщая результаты опытов, можно заметить, что ускорение, приобретаемое телом, прямо пропорционально силе, действующей на тело, и обратно пропорционально массе данного тела (второй закон ньютона формулировка).

Этот вывод называется вторым законом Ньютона. Математически этот закон можно записать так (формула второго закона ньютона):

а = F /m

где а — ускорение, m—масса тела, F — результирующая всех сил, приложенных к телу. В частном случае на тело может действовать и одна сила.

Результирующая сила F равна векторной сумме всех сил, приложенных к телу;

F = mа.

Следовательно, сила равна произведению массы на ускорение.

Второй закон динамики можно записать в иной более удобной форме. Учитывая, что ускорение

а = (υ₂ — υ₁) / (t₂ — t₁)

подставим это выражение в уравнение второго закона Ньютона. Получим

F = ma = (mυ₂ — mυ₁) / (t₂ — t₁) = (∆(mυ))/∆t

Что такое импульс

Импульсом, или количеством движения, называется вектор, равный произведению массы тела на его скорость (тυ).

Тогда основной закон динамики можно сформулировать следующим образом: сила равна изменению импульса в единицу времени (второй закон ньютона в импульсной форме)

F = (∆(mυ))/∆t

Это и есть наиболее общая формулировка второго закона Ньютона. Массу тела Ньютон определил как количество вещества, содержащегося в данной теле. Это определение несовершенно.

Из второго закона Ньютона вытекает следующее определение массы. Из равенства

a₁/a₂= m₂/m₁

видно, что чем больше масса тела, тем меньше ускорение получает тело, то есть тем труднее изменить скорость этого тела и наоборот.

Следовательно, чем больше масса тела, тем в большей степени это тело способно сохранять скорость неизменной, то есть больше инертности. Тогда можно сказать, что масса есть мера инертности тела.

Эйнштейн доказал, что масса тела остается постоянной только при определенных условиях. В зависимости от скорости движения тела его масса изменяется по такому закону:

Масса тела

где m — масса тела, движущегося со скоростью υ; m₀ — масса этого же тела, находящегося в покое; с = 3 • 10⁸м/с скорость света в вакууме.

Проанализируем данное уравнение:

Если υ«с, то величиной —, как очень малой, можно пренебречь и m = m₀, то есть при скоростях движения, много меньших скорости света, масса тела не зависит от скорости движения;
Если υ ≈ с, то υ₂/с₂ ≈ 1, тогда т = m₀/0— отсюда вытекает, что m → ∞.

По мере увеличения скорости тела для его дальнейшего ускорения нужно будет прикладывать все увеличивающиеся силы.

Но бесконечно больших сил, которые потребовались бы для сообщения телу скорости, равной скорости света, в природе не существует.

Таким образом, заставить рассматриваемое тело двигаться со скоростью света принципиально невозможно.

Со скоростями, близкими к скорости света, современная физика встречается: так разгоняются, например, элементарные частицы в ускорителях.

Масса тела с ростом скорости

Масса тела с ростом скорости увеличивается, но количество вещества остается неизменным, возрастает инертность. Поэтому массу нельзя путать с количеством вещества.

Покажем связь между силой тяжести, массой тела и ускорением свободного падения. Любое тело, поднятое над Землей и ничем не поддерживаемое, падает снова на Землю.

Это происходит вследствие того, что между телом и Землей существует притяжение (этот вопрос более подробно рассмотрим позже).

Сила, с которой тело притягивается к Земле, называется силой тяжести. Падение тел в безвоздушном пространстве под действием силы тяжести (при υ₀= 0) называется свободным падением.

Отметим, что для тел, покоящихся в поле сил тяготения, сила тяжести равна весу тела Р.

Весом тела называется сила, с которой тело давит на горизонтальную подставку, неподвижную относительно Земли, или действует на подвес.

Если Р— сила тяжести, m — масса, g — ускорение силы тяжести (в данной точке Земли оно для всех тел одинаковой среднее его значение равно 9,8м/с²), то применяя второй закон динамики, получим

P = mg.

Выразим с помощью этой формулы веса двух различных тел. Тогда:

P₁ = m₁g и Р₂ = m₂g. Разделив почленно эти два равенства, будем иметь

P₁/P₂ = m₁/m₂

Следовательно, веса тел в данной точке земной поверхности прямо пропорциональны их массам.

Задачи на второй закон ньютона

1. Какая сила F действует на автомобиль массой кгm=1000 кг, если он движется с ускорением мсa=1 м/с².

Дано:
m = 1000 кг
a = 1 м/с²

Найти: F — ?

Решение:

Запишем второй закон Ньютона :

F = mа.

F = 1000 кг • 1 м/с²= 1000 Н

Ответ: 1000 Н.

2. На мяч действует сила F = 70Н, масса мяча m = 0,2 кг, найти его ускорение a.

Дано:

m = 0,2 кг,

F = 70Н

Найти:

a — ?

Решение:

Запишем второй закон Ньютона :

F = mа.

Следовательно а = F / m.

а = 70Н : 0,2 кг = 350 м/с.

Ответ: а = 350 м/с.

Статья на тему Второй закон Ньютона

Источник

Второй закон Ньютона в классической механике[править | править код]

Возможные формулировки[править | править код]

Область применения закона[править | править код]

Логическая роль второго закона Ньютона[править | править код]

Запись закона в разных системах координат[править | править код]

Второй закон за пределами классической механики[править | править код]

В релятивистской динамике[править | править код]

В квантовой механике[править | править код]

Научно-историческое значение закона[править | править код]

Лагранжево и гамильтоново обобщения закона[править | править код]

См. также[править | править код]

Примечания[править | править код]

Ссылки[править | править код]

2-ой закон Ньютона, определение и формула

Равнодействующая сила

Первый закон Ньютона

Второй закон Ньютона

Третий закон Ньютона

Пример задачи на законы Ньютона

Исаак Ньютон: мифы и факты из жизни

Что такое второй закон Ньютона, масса и вес тела

Ускорение от величины силы

Зависимость ускорения от массы

Что такое импульс

Масса тела с ростом скорости

Задачи на второй закон ньютона

Вам также может понравиться

Как найти людей бессмертный полк

У приложения файлы нет права установки приложений как исправить

Отслоилась стяжка как исправить

Добавить комментарий Отменить ответ