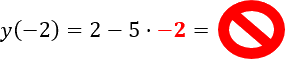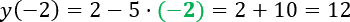Прежде чем перейти к разбору решения задач с функциями обязательно прочитайте урок
«Что такое функция в математике».
После того, как вы действительно поймете, что такое функция
(возможно, придется прочитать урок не один раз) вы с бóльшей уверенностью сможете решать задания с функциями.
В этом уроке мы разберем, как решать основные типы задач на функцию и графики функций.
Как получить значение функции
Рассмотрим задание.
Функция задана формулой «y = 2x − 1»
- Вычислить «y» при «x = 15»
- Найти значение «x», при котором
значение «y» равно «−19».
Для того, чтобы вычислить «y» при
«x = 15» достаточно подставить в функцию вместо «x»
необходимое числовое значение.
Запись решения выглядит следующим образом.
y(15) = 2 · 15 − 1 = 30 − 1 = 29
Для того, чтобы найти «x»
по известному «y», необходимо подставить вместо
«y» в формулу функции числовое значение.
То есть теперь наоборот, для поиска «x»
мы подставляем в функцию «y = 2x − 1» вместо
«y» число «−19» .
−19 = 2x − 1
Мы получили линейное уравнение с неизвестным «x»,
которое решается по правилам решения линейных уравнений.
Запомните!
Не забывайте про правило переноса в уравнениях.
При переносе из левой части уравнения в правую (и наоборот) буква или число меняет знак на
противоположный.
−19 = 2x − 1
0 = 2x − 1 + 19
−2x = −1 + 19
−2x = 18
Как и при решении линейного уравнения, чтобы найти неизвестное, сейчас
требуется умножить и левую, и правую часть на «−1» для смены знака.
−2x = 18 | · (−1)
2x = −18
Теперь разделим и левую, и правую часть на «2», чтобы найти «x» .
2x = −18 | (: 2)
x = −9
Как проверить верно ли равенство для функции
Рассмотрим задание.
Функция задана формулой «f(x) = 2 − 5x».
Верно ли равенство
«f(−2) = −18»?
Чтобы проверить верно ли равенство, нужно подставить в функцию «f(x) = 2 − 5x»
числовое значение «x = −2» и сопоставить с тем, что получится при расчетах.
Важно!
Когда подставляете отрицательное число вместо «x», обязательно заключайте его в скобки.
Не забывайте использовать
правило знаков.
Неправильно
Правильно
С помощью расчетов мы получили
«f(−2) = 12».
Это означает, что «f(−2) = −18»
для функции «f(x) = 2 − 5x» не является верным равенством.
Как проверить, что точка принадлежит графику функции
Рассмотрим функцию «y = x2 −5x + 6»
Требуется выяснить, принадлежит ли графику этой функции точка с координатами
(1; 2).
Для этой задачи нет необходимости, строить график заданной функции.
Запомните!
Чтобы определить, принадлежит ли точка функции,
достаточно подставить её координаты в функцию (координату по оси
«Ox» вместо
«x» и координату по оси «Oy»
вместо «y»).
Если получится верное равенство, значит, точка принадлежит функции.
Вернемся к нашему заданию. Подставим в функцию «y = x2 − 5x + 6»
координаты точки (1; 2).
Вместо «x» подставим «1».
Вместо «y» подставим «2».
2 = 12 − 5 · 1 + 6
2 = 1 − 5 + 6
2 = −4 + 6
2 = 2 (верно)
У нас получилось верное равенство, значит, точка с координатами
(1; 2) принадлежит заданной функции.
Теперь проверим точку с координатами (0; 1).
Принадлежит ли она
функции «y = x2 − 5x + 6»?
Вместо «x» подставим «0».
Вместо «y» подставим «1».
1 = 02 − 5 · 0 + 6
1 = 0 − 0 + 6
1 = 6 (неверно)
В этом случае мы не получили верное равенство.
Это означает, что точка с координатами (0; 1) не принадлежит функции
«y = x2 − 5x + 6»
Как получить координаты точки функции
С любого графика функции можно снять координаты точки. Затем необходимо убедиться, что при подстановке координат
в формулу функции получается верное равенство.
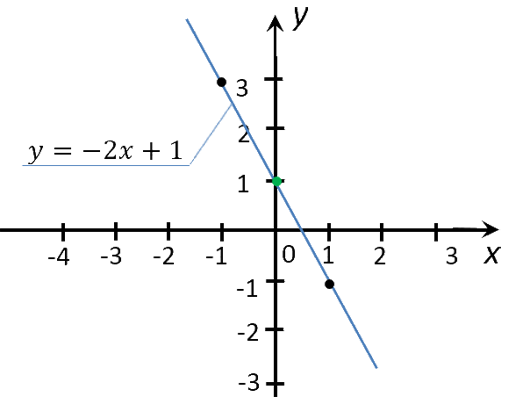
Рассмотрим функцию «y(x) = −2x + 1». Её график
мы уже
строили
в предыдущем уроке.
Найдем на графике функции «y(x) = −2x + 1», чему равен «y»
при x = 2.
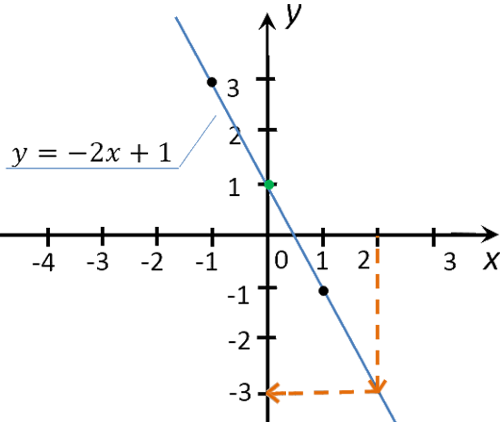
Для этого из значения «2» на оси «Ox» проведем перпендикуляр к графику функции.
Из точки пересечения перпендикуляра и графика функции проведем еще один перпендикуляр к оси «Oy».
Полученное значение «−3» на оси «Oy» и будет искомым значением «y».
Убедимся, что мы правильно сняли координаты точки для x = 2
в функции «y(x) = −2x + 1».
Для этого мы подставим x = 2 в формулу функции
«y(x) = −2x + 1». Если мы правильно
провели перпендикуляр, мы также должны получить в итоге y = −3.
y(2) = −2 · 2 + 1 = −4 + 1 = −3
При расчетах мы также получили y = −3.
Значит, мы правильно получили координаты с графика функции.
Важно!
Все полученные координаты точки с графика функции обязательно проверяйте
подстановкой значений «x» в функцию.
При подстановке числового значения «x» в функцию в результате должно получиться
то же значение «y», которое вы получили на графике.
При получении координат точек с графика функции высока вероятность, что вы ошибетесь, т.к. проведение перпендикуляра к осям выполняется «на глазок».
Только подстановка значений в формулу функции дает точные результаты.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
11 ноября 2018 в 15:46
Веточка Сакуры
Профиль
Благодарили: 0
Сообщений: 1
Веточка Сакуры
Профиль
Благодарили: 0
Сообщений: 1
Функция y=f(x) является нечётной и при x ⩽0 задаётся формулой y= – x² — 8x.Найдите значение фун. в т. минимума (y min).
0
Спасибо
Ответить
12 ноября 2018 в 3:25
Ответ для Веточка Сакуры
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
ymin = y(4) = -16.
0
Спасибо
Ответить
17 сентября 2018 в 13:28
Alesger Mammedov
Профиль
Благодарили: 0
Сообщений: 1
Alesger Mammedov
Профиль
Благодарили: 0
Сообщений: 1
Добрый день помогите пожалуйста с задачкой
f(x2-3x)=3x2+5x-4
f(3)=?
0
Спасибо
Ответить
17 сентября 2018 в 23:01
Ответ для Alesger Mammedov
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
f(3) = 26 ± 7√21
0
Спасибо
Ответить
13 ноября 2016 в 6:43
Роман Безбородов
Профиль
Благодарили: 0
Сообщений: 1
Роман Безбородов
Профиль
Благодарили: 0
Сообщений: 1
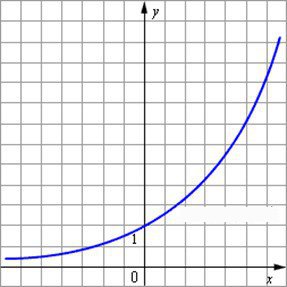
0
Спасибо
Ответить
14 ноября 2016 в 17:30
Ответ для Роман Безбородов
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
y = ax; a > 1.
0
Спасибо
Ответить
7 сентября 2016 в 22:08
Иван Баранов
Профиль
Благодарили: 0
Сообщений: 3
Иван Баранов
Профиль
Благодарили: 0
Сообщений: 3
у=Х2+2Х-3 найдите значение функции, если значение аргумента равно -2
у=3х-5 при каком значении аргумента значение функции раво 10
0
Спасибо
Ответить
8 сентября 2016 в 15:26
Ответ для Иван Баранов
Юлия Анарметова
Профиль
Благодарили: 0
Сообщений: 11
Юлия Анарметова
Профиль
Благодарили: 0
Сообщений: 11
аргумент это х значит у=(-2)2+2 · (-2)-3=4-4-3=-3
у=3х-5 значит 10=3х-5
10+5=3х
15=3х
х=15:3=5
0
Спасибо
Ответить
Как найти значение функции
Под понятием функции в математике понимают связь между элементами множеств. Если говорить более точно, это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).
Вам понадобится
- Знания в области алгебры и математического анализа.
Инструкция
Значения функции это некая область, значения из которой может принимать функция. Например область значения функции f(x)=|x| от 0 до бесконечности. Чтобы найти значение функции в конкретной точке необходимо подставить вместо аргумента функции его числовой эквивалент, полученное число и будет значением функции. Пусть дана функция f(x)=|x| – 10 + 4x. Найдем значение функции в точке x=-2. Подставим вместо x число -2: f(-2)=|-2| – 10 + 4*(-2) = 2 – 10 – 8 = -16. То есть значение функции в точке -2 равно -16.
Обратите внимание
Прежде чем искать значение функции в точке – убедитесь, что она входит в область определения функции.
Полезный совет
Аналогичным способом можно найти значение функции нескольких аргументов. Отличие в том, что вместо одного числа необходимо будет подставить несколько – по числу аргументов функции.
Функция — это математическое выражение, которое описывает зависимость одной величины от другой. Она может быть представлена как алгоритм, который преобразует входные данные в выходные данные. Решение функции означает нахождение значения функции при заданных входных данных.
Алгоритм решения функции
Для того чтобы решить функцию, необходимо знать ее математическое выражение и значения входных параметров. Алгоритм решения функции следующий:
- Подставьте значения входных параметров в математическое выражение функции.
- Вычислите значение функции.
- Полученное значение является результатом решения функции.
Пример решения функции:
Рассмотрим функцию y = 2x + 1. Найдем значение функции при x = 3.
- Подставляем значение x = 3 в математическое выражение: y = 2*3 + 1 = 7.
- Вычисляем значение функции: y = 7.
- Полученное значение является результатом решения функции: y = 7 при x = 3.
Вычисление значения функции
Вычисление значения функции может быть выполнено различными способами. Рассмотрим некоторые из них:
Вычисление значения функции с помощью таблицы значений
Для вычисления значения функции с помощью таблицы значений необходимо построить таблицу, в которой указываются значения входных параметров и соответствующие им значения функции. Затем необходимо найти значение функции при заданных входных параметрах в этой таблице.
Вычисление значения функции графически
График функции — это геометрическое представление зависимости значения функции от входных параметров. Для того чтобы вычислить значение функции графически, необходимо на графике функци найти значение функции при заданных входных параметрах. Для этого необходимо провести вертикальную линию через значение заданного входного параметра и найти точку пересечения этой линии с графиком функции. Значение функции в этой точке будет соответствовать искомому значению функции при заданных входных параметрах.
Вычисление значения функции с помощью программного кода
Для вычисления значения функции с помощью программного кода необходимо написать код, который будет выполнять математическое выражение функции с заданными входными параметрами и возвращать результат. Пример программного кода для функции y = 2x + 1:
def calculate_y(x):
y = 2*x + 1
return y
Для вычисления значения функции при заданном входном параметре необходимо вызвать функцию calculate_y с этим параметром:
y = calculate_y(3)
print(y) # Выводит 7
Заключение
Решение функций является важной задачей в математике и других науках. Для того чтобы правильно решать функции и находить значения функций, необходимо знать алгоритм решения и уметь применять различные методы вычисления. Надеемся, что данная статья поможет вам разобраться в этой теме и успешно решать функции.
Вычисление значений функции
Онлайн калькулятор поможет найти значения функции в заданном интервале, построить таблицу значений функции онлайн, табулировать функцию.
Вычисляет значения функции одной переменной y для заданных значений переменной x. Функция задается при помощи формулы, пример:
Построить таблицу значений функции f(x)=x/(x+1) на отрезке от 0 до 6 с шагом в единицу.
Синтаксис
основных функций:
xa: x^a
|x|: abs(x)
√x: Sqrt[x]
n√x: x^(1/n)
ax: a^x
logax: Log[a, x]
ln x: Log[x]
cos x: cos[x] или Cos[x]
sin x: sin[x] или Sin[x]
tg: tan[x] или Tan[x]
ctg: cot[x] или Cot[x]
sec x: sec[x] или Sec[x]
cosec x: csc[x] или Csc[x]
arccos x: ArcCos[x]
arcsin x: ArcSin[x]
arctg x: ArcTan[x]
arcctg x: ArcCot[x]
arcsec x: ArcSec[x]
arccosec x: ArcCsc[x]
ch x: cosh[x] или Cosh[x]
sh x: sinh[x] или Sinh[x]
th x: tanh[x] или Tanh[x]
cth x: coth[x] или Coth[x]
sech x: sech[x] или Sech[x]
cosech x: csch[x] или Csch[е]
areach x: ArcCosh[x]
areash x: ArcSinh[x]
areath x: ArcTanh[x]
areacth x: ArcCoth[x]
areasech x: ArcSech[x]
areacosech x: ArcCsch[x]
конъюнкция “И” ∧: &&
дизъюнкция “ИЛИ” ∨: ||
отрицание “НЕ” ¬: !
импликация =>
число π pi : Pi
число e: E
бесконечность ∞: Infinity, inf или oo
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Для начала разберемся с тем, как находить значение функции при заданном значении аргумента. Для того чтобы определить значение функции, зная при этом значение аргумента, необходимо подставит известное нам число в уравнение функции и вычислить то, чему равен y.
Но бывает и такое, что заданное значение аргумента недопустимо, т.е. не входит в область допустимых значений функции. В данном случае значение функции считается неопределенным.
Для закрепления полученного материала приведем пример. Допустим у нас есть функция y = 3x^2 — 4x + 1, где нам необходимо найти y(0); y(1); y(-2); y(3).
Для начала найдем y(0). У нас получится y(0) = 3 * 0^2 — 4 * 0 + 1 = 1.
По такому же принцип найдем и все остальные значения:
y(1) = 3 * 1^2 — 4 * 1 + 1 = 3 — 4 + 1 = 0;
y(-2) = 3 * (-2)^2 — 4 * (-2) + 1 = 12 + 8 + 1 = 21;
y(3) = 3 * 3^2 — 4 * 3 + 1 = 27 — 12 + 1 = 16.
Ответ записывается путем перечисления найденных значений при конкретном аргументе.
Ответ: y(0) = 1; y(1) = 0; y(-2) = 21; y(3) = 16.
Разберем еще один пример, но только теперь с корнем. Например, функция y = √x — 3, для которой необходимо найти y(4); y(7); y(2).
Начнем с условия, при котором аргумент равен 4: y(4) = √4-3 = √1 = 1. При данном решении мы использовали правила, согласно которому корень из 1 равен самой 1. Подобным образом находим значение функции при других аргументах:
y(7) = √7-3 = √4 = 2. Таким образом значение функции при x = 7 равно 2;
y(2) = √2-3 = √-1 — значение не определено, поскольку пользуясь свойствами корней, мы вспоминаем, что отрицательных корней быть не может.
Ответ: y(4) = 1; y(7) = 2; y(2) не существует.
Теперь, разобравшись в том, как найти функцию при известном аргументе, можно перейти к изучению обратного процесса — нахождению значения аргумента при котором функция принимает заданное значение. Данные задачи имеют определенный алгоритм решения, которого стоит придерживаться.
Во-первых, чтобы найти значения x, при которых функция y(x) принимает заданное значение, необходимо правую часть уравнения приравнять к известному по условию числу. Затем мы решаем полученное уравнение и ищем корни переменной x.
А как мы знаем из темы уравнений, то корень может быть как один, так и два, а может быть и не одного верного значения. Последнее происходит в тех случаях, когда функция не принимает указанное значение ни при каком значении аргумента.
Теперь закрепим теорию практикой и рассмотрим пример: y = -x + 5, где y = 3. Пользуясь вышеописанным алгоритмом решения, составим уравнение: -x + 5 = 3. Теперь решим его относительно x:
-x + 5 = 3 — для удобства перенесем -5 в правую сторону;
Итогом предыдущего действия будет: -x = 3-5 или -x = -2. Умножим левую и правую часть уравнения на -1, чтобы избавиться от “-”;
Получим x = 2. Таким образом, при x = 2 функция y = — x + 5 принимает значение 3. Запишем получившийся ответ.
Ответ: при x = 2.
Рассмотрим еще один более трудный пример, где есть степень: y = (x — 2)^2, где y приравнен 1. Как и в предыдущем примере заменим y заданным условием значением. В итоге у нас получится:
(x — 2)^2 = 1. Данное уравнение необходимо решить;
Чтобы избавиться от степени разности, нам необходимо также представить 1 в квадрате и затем опустить его. Итогом данных действий может стать два варианта:
x — 2 = 1 или x — 2 = -1. Рассмотрим каждый по отдельности.
x — 2 = 1;
x = 1 + 2;
x = 3.
В случае же с x — 2 = -1 получится:
x — 2 = -1;
x = -1 + 2;
x = 1.
Осталось только записать ответ.
Ответ: x = 1; x = 3.
Таким образом, данная тема является достаточно простой и доступной, однако, она очень важна в решении многих задач. Самое главное здесь — это знание различных свойств дробей, корней, степеней и т.д. Если вы чувствуете, что не совсем владеете этими темами, то вернитесь к ним и повторите их.