Высота правильной четырехугольной призмы как найти

Как найти высоту четырёхугольной призмы

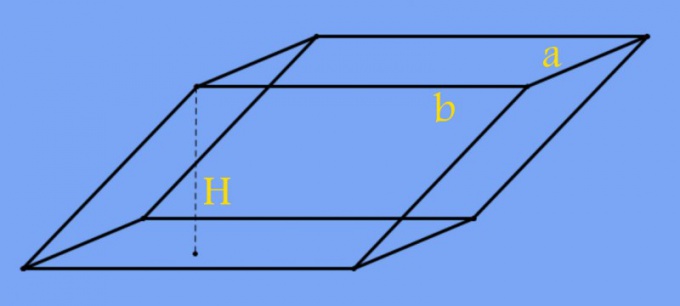
Призмой называют объемную фигуру, составленную из некоторого количества прямоугольных боковых граней и двух параллельных друг другу оснований. Основания могут иметь форму любого многоугольника, включая и четырехугольник. Высотой этой фигуры называют перпендикулярный основаниям отрезок между плоскостями, в которых они лежат. Его длина в общем случае определяется углом наклона боковых граней к основаниям призмы.

Инструкция

Если в условиях задачи приведен объем (V) пространства, ограниченного гранями призмы, и площадь ее основания (s), для вычисления высоты (H) используйте формулу, общую для призм с основанием любой геометрической формы. Разделите объем на площадь основания: H=V/s. Например, при объеме в 1200 см³ и площади основания, равной 150 см², высота призмы должна быть равна 1200/150=8 см.

Если четырехугольник, лежащий в основании призмы, имеет форму какой-либо правильной фигуры, вместо площади в вычислениях можно использовать длины ребер призмы. Например, при квадратном основании площадь в формуле предыдущего шага замените второй степенью длины его ребра (a):H=V/a². А в случае прямоугольника в ту же формулу подставьте произведение длин двух смежных ребер основания (a и b):H=V/(a*b).

Для вычисления высоты (H) правильной четырехугольной призмы может оказаться достаточным знания полной площади поверхности (S) и длины одного ребра основания (a). Так как общая площадь складывается из площадей двух оснований и четырех боковых граней, а в таком многограннике основанием является квадрат, площадь одной боковой поверхности должна быть равна (S-a²)/4. Эта грань имеет два общих ребра с квадратными основаниями известного размера, значит, для вычисления длины другого ребра разделите полученную площадь на сторону квадрата: (S-a²)/(4*a). Так как рассматриваемая призма является прямоугольной, то ребро вычисленной вами длины примыкает к основаниям под углом 90°, т.е. совпадает с высотой многогранника: H=(S-a²)/(4*a).

В правильной четырехугольной призме для вычисления высоты (H) достаточно знания длины диагонали (L) и одного ребра основания (a). Рассмотрите треугольник, образуемый этой диагональю, диагональю квадратного основания и одним из боковых ребер. Ребро здесь – неизвестная величина, совпадающая с искомой высотой, а диагональ квадрата, основываясь на теореме Пифагора, равна произведению длины стороны на корень из двойки. В соответствии с той же теоремой выразите искомую величину (катет) через длины диагонали призмы (гипотенузы) и диагонали основания (второй катет): H=√(L²-(a*V2)²)=√(L²-2*a²).

Источники:

• четырехугольная призма

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

В школьном курсе стереометрии одной из самых простых фигур, которая имеет не нулевые размеры вдоль трех пространственных осей, является четырехугольная призма. Рассмотрим в статье, что это за фигура, из каких элементов она состоит, а также как можно рассчитать площадь ее поверхности и объем.

Понятие о призме

В геометрии призмой полагают пространственную фигуру, которая образована двумя одинаковыми основаниями и боковыми поверхностями, которые соединяют стороны этих оснований. Отметим, что оба основания переходят друг в друга с помощью операции параллельного переноса на некоторый вектор. Такое задание призмы приводит к тому, что все ее боковые стороны всегда являются параллелограммами.

Количество сторон основания может быть произвольным, начиная от трех. При стремлении этого числа к бесконечности, призма плавно переходит в цилиндр, поскольку ее основание становится кругом, а боковые параллелограммы, соединяясь, образуют цилиндрическую поверхность.

Как и любой полиэдр, призма характеризуется сторонами (плоскости, которые ограничивают фигуру), ребрами (отрезки, по которым пересекаются две любые стороны) и вершинами (точки встречи трех сторон, для призмы две из них являются боковыми, а третья – основанием). Количества названных трех элементов фигуры связаны между собой следующим выражением:

Р = С + В – 2

Здесь Р, С и В – это число ребер, сторон и вершин, соответственно. Это выражение является математической записью теоремы Эйлера.

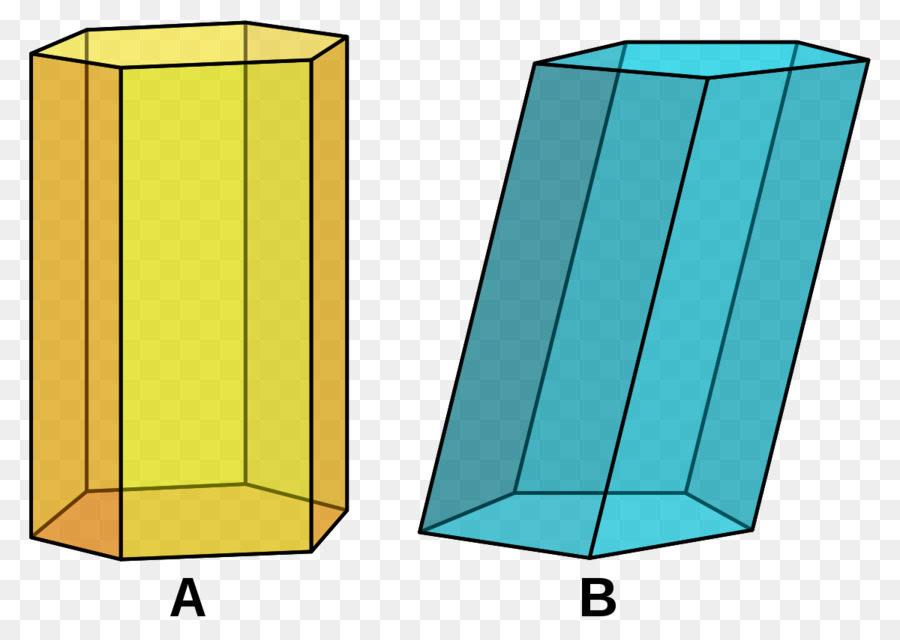
Выше приведен рисунок, где показаны две призмы. В основании одной из них (A) лежит правильный шестиугольник, и стороны боковые перпендикулярны основаниям. Рисунок B демонстрирует другую призму. Ее боковые стороны уже не перпендикулярны основаниям, а основание представляет собой правильный пятиугольник.

Что такое призма четырехугольная?

Как понятно из описания выше, тип призмы в первую очередь определяется видом многоугольника, который образует основание (оба основания одинаковые, поэтому речь можно вести об одном из них). Если этим многоугольником является параллелограмм, то мы получаем четырехугольную призму. Таким образом, все стороны этого вида призмы являются параллелограммами. Четырехугольная призма имеет собственное название – параллелепипед.

Количество сторон параллелепипеда равно шести, причем каждая сторона имеет аналогичную параллельную ей. Поскольку основания параллелепипеда – это две стороны, то оставшиеся четыре являются боковыми.

Количество вершин параллелепипеда равно восьми, в чем легко убедиться, если вспомнить, что вершины призмы образуются только на вершинах базовых многоугольников (4х2=8). Применяя теорему Эйлера, получаем число ребер:

Р = С + В – 2 = 6 + 8 – 2 = 12

Из 12-ти ребер, только 4 образованы самостоятельно боковыми сторонами. Остальные 8 лежат в плоскостях оснований фигуры.

Далее в статье речь пойдет только о четырехугольных призмах.

Виды параллелепипедов

Первый тип классификации заключается в особенности параллелограмма, лежащего в основании. Он может быть следующего вида:

• обычный, у которого углы не равны 90^o;
• прямоугольник;
• квадрат – правильный четырехугольник.

Второй тип классификации заключается в угле, при котором боковая сторона пересекает основание. Здесь возможно два разных случая:

• этот угол не является прямым, тогда призму называют косоугольной или наклонной;
• угол равен 90^o, тогда такая призма является прямоугольной или просто прямой.

Третий тип классификации связан с высотой призмы. Если призма является прямоугольной, и в основании лежит либо квадрат, либо прямоугольник, тогда ее называют прямоугольным параллелепипедом. Если же в основании находится квадрат, призма является прямоугольной, а ее высота равна длине стороны квадрата, то мы получаем всем известную фигуру куб.

Поверхность призмы и ее площадь

Совокупность всех точек, которые лежат на двух основаниях призмы (параллелограммах) и на ее боковых сторонах (четыре параллелограмма), образуют поверхность фигуры. Площадь этой поверхности может быть вычислена, если рассчитать площадь основания и эту величину для боковой поверхности. Тогда их сумма даст искомое значение. Математически это записывается так:

S = 2*S_o + S_b

Здесь S_o и S_b – площадь основания и боковой поверхности, соответственно. Цифра 2 перед S_o появляется в виду того, что оснований два.

Отметим, что записанная формула справедлива для любой призмы, а не только для площади четырехугольной призмы.

Полезно напомнить, что площадь параллелограмма S_p вычисляется по формуле:

S_p = a*h

Где символы a и h обозначают длину одной из его сторон и высоту, проведенную к этой стороне, соответственно.

Площадь прямоугольной призмы с квадратным основанием

В правильной четырехугольной призме основание представляет собой квадрат. Обозначим для определенности его сторону буквой a. Чтобы рассчитать площадь правильной четырехугольной призмы, следует знать ее высоту. Согласно определению для этой величины, она равна длине перпендикуляра, опущенного из одного основания на другое, то есть равна расстоянию между ними. Обозначим ее буквой h. Поскольку все боковые грани перпендикулярны основаниям для рассматриваемого типа призмы, то высота правильной четырехугольной призмы будет равна длине ее бокового ребра.

В общей формуле для площади поверхности призмы стоит два слагаемых. Площадь основания в данном случае рассчитать просто, она равна:

S_o = a²

Чтобы вычислить площадь боковой поверхности, рассуждаем следующим образом: эта поверхность образована 4-мя одинаковыми прямоугольниками. Причем стороны каждого из них равны a и h. Это означает, что площадь S_b буде равна:

S_b = 4*a*h

Заметим, что произведение 4*a – это периметр квадратного основания. Если обобщить это выражение на случай произвольного основания, тогда для прямоугольной призмы боковую поверхность можно рассчитать так:

S_b = P_o*h

Где P_o – периметр основания.

Возвращаясь к задаче расчета площади правильной четырехугольной призмы, можно записать итоговую формулу:

S = 2*S_o + S_b = 2*a² + 4*a*h = 2*a*(a+2*h)

Площадь косоугольного параллелепипеда

Вычислить ее несколько сложнее, чем для прямоугольного. В этом случае площадь основания четырехугольной призмы вычисляется по той же формуле, что и для параллелограмма. Изменения касаются способа определения площади боковой поверхности.

Для этого используется та же формула через периметр, что приведена в пункте выше. Только теперь в ней появятся несколько иные множители. Общая формула для S_b в случае косоугольной призмы имеет вид:

S_b = P_sr*c

Здесь с – это длина бокового ребра фигуры. Величина P_sr является периметром прямоугольного среза. Строится этот сред следующим образом: необходимо плоскостью пересечь все боковые грани таким образом, чтобы она была перпендикулярна всем им. Образованный прямоугольник и будет искомым срезом.

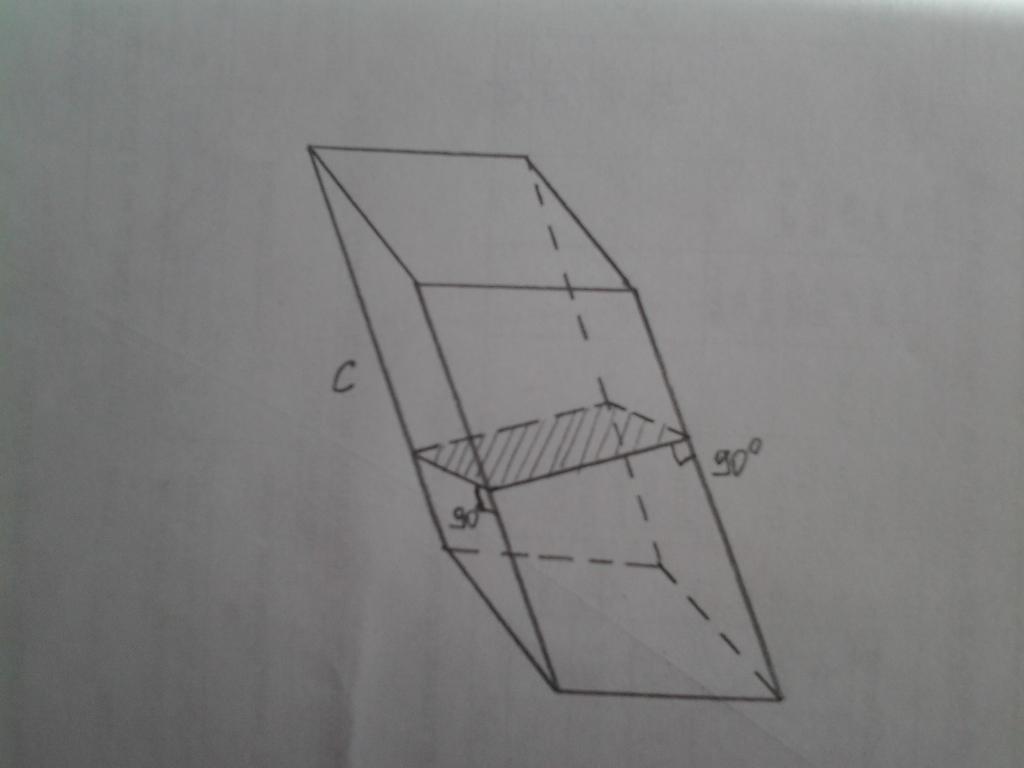
На рисунке выше приведен пример косоугольного параллелепипеда. Заштрихованное его сечение с боковыми сторонами образует прямые углы. Периметр сечения равен P_sr. Он образован четырьмя высотами боковых параллелограммов. Для этой четырехугольной призмы площадь боковой поверхности рассчитывается по указанной выше формуле.

Длина диагонали прямоугольного параллелепипеда

Диагональ параллелепипеда – это отрезок, который соединяет две вершины, не имеющие общих сторон, которые их образуют. В любой четырехугольной призме диагоналей всего четыре. Для прямоугольного параллелепипеда, в основании которого расположен прямоугольник, длины всех диагоналей равны друг другу.

Ниже на рисунке приведена соответствующая фигура. Красный отрезок является ее диагональю.

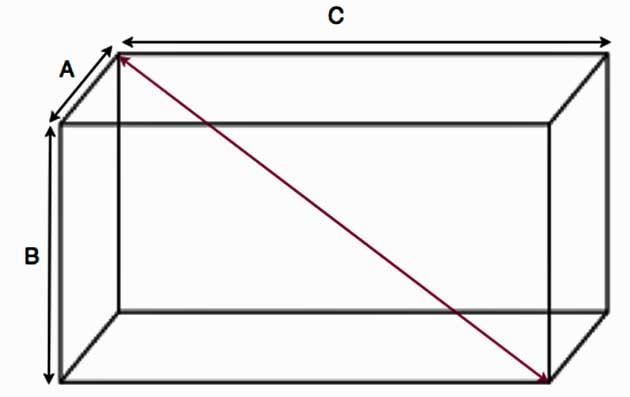
Рассчитать ее длину очень просто, если вспомнить о теореме Пифагора. Каждый школьник может получить искомую формулу. Она имеет следующую форму:

D = √(A² + B² + C²)

Здесь D – длина диагонали. Остальные символы – это длины сторон параллелепипеда.

Многие путают диагональ параллелепипеда с диагоналями его сторон. Ниже приводится рисунок, где цветными отрезками изображены диагонали сторон фигуры.

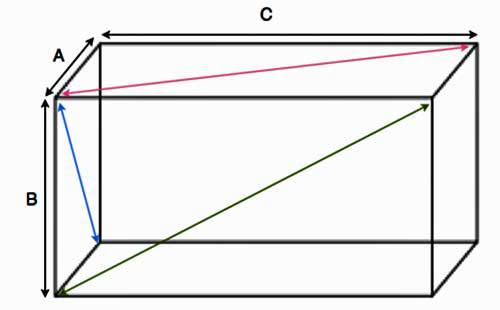
Длина каждой из них также определяется по теореме Пифагора и равна квадратному корню из суммы квадратов соответствующих длин сторон.

Объем призмы

Помимо площади правильной четырехугольной призмы или других видов призм, для решения некоторых геометрических задач следует знать и их объем. Эта величина для абсолютно любой призмы вычисляется по следующей формуле:

V = S_o*h

Если призма является прямоугольной, тогда достаточно вычислить площадь ее основания и умножить его на длину ребра боковой стороны, чтобы получить объем фигуры.

Если призма является правильной четырехугольной, тогда ее объем будет равен:

V = a² *h.

Легко видеть, что эта формула преобразуется в выражение для объема куба, если длина бокового ребра h равна стороне основания a.

Задача с прямоугольным параллелепипедом

Для закрепления изученного материала решим следующую задачу: имеется прямоугольный параллелепипед, стороны которого равны 3 см, 4 см и 5 см. Необходимо рассчитать площадь его поверхности, длину диагонали и объем.

Для определенности будем считать, что основанием фигуры является прямоугольник со сторонами 3 см и 4 см. Тогда его площадь равна 12 см², а период составляет 14 см. Используя формулу для площади поверхности призмы, получаем:

S = 2*S_o + S_b = 2*12 + 5*14 = 24 + 70 = 94 см²

Для определения длины диагонали и объема фигуры можно непосредственно воспользоваться приведенными выше выражениями:

D = √(3²+4²+5²) = 7,071 см;

V = 3*4*5 = 60 см³.

Задача с косоугольным параллелепипедом

Ниже на рисунке изображена косоугольная призма. Ее стороны равны: a=10 см, b = 8 см, с = 12 см. Необходимо найти площадь поверхности этой фигуры.

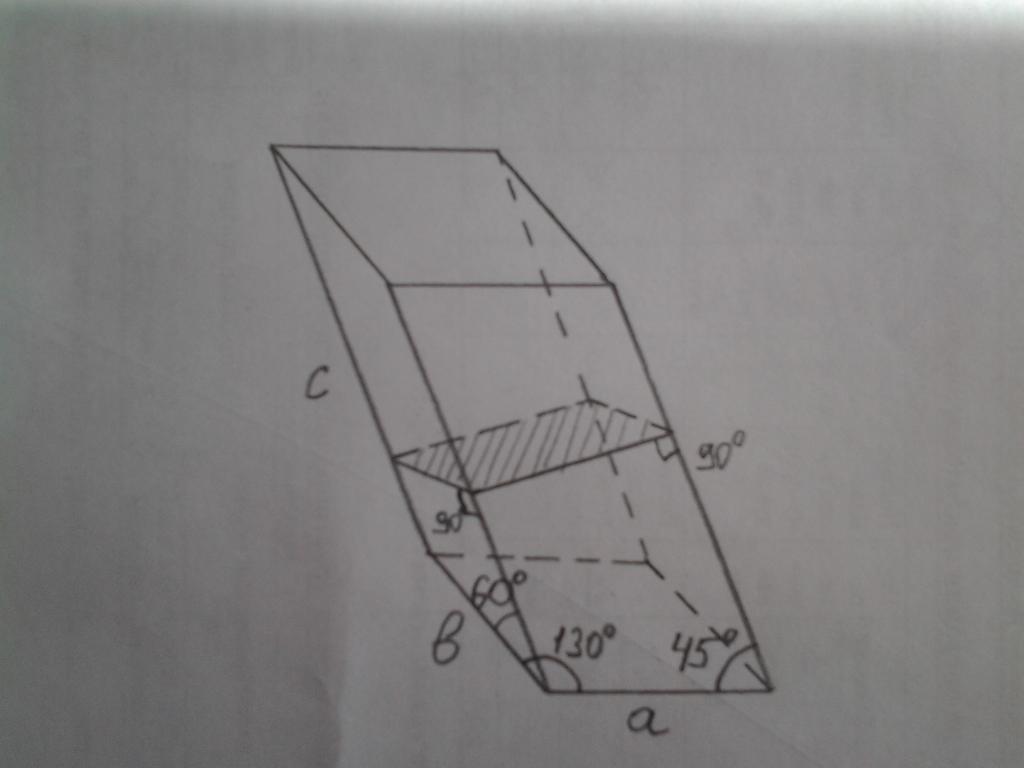
Сначала определим площадь основания. Из рисунка видно, что острый угол равен 50^o. Тогда его площадь равна:

S_o = h*a = sin(50^o)*b*a

Для определения площади боковой поверхности, следует найти периметр заштрихованного прямоугольника. Стороны этого прямоугольника равны a*sin(45^o) и b*sin(60^o). Тогда периметр этого прямоугольника равен:

P_sr = 2*(a*sin(45^o)+b*sin(60^o))

Полная площадь поверхности этого параллелепипеда равна:

S = 2*S_o + S_b = 2*(sin(50^o)*b*a + a*c*sin(45^o) + b*c*sin(60^o))

Подставляем данные из условия задачи для длин сторон фигуры, получаем ответ:

S = 458,5496 см³

Из решения этой задачи видно, что для определения площадей косоугольных фигур используются тригонометрические функции.

Правильная четырехугольная призма

Определение.

Правильная четырехугольная призма – это шестигранник, основаниями которого являются два равных квадрата, а боковые грани представляют собой равные прямоугольники

Боковое ребро – это общая сторона двух смежных боковых граней

Высота призмы – это отрезок, перпендикулярный основаниям призмы

Диагональ призмы – отрезок, соединяющий две вершины оснований, которые не принадлежат к одной грани

Диагональная плоскость – плоскость, которая проходит через диагональ призмы и ее боковые ребра

Диагональное сечение – границы пересечения призмы и диагональной плоскости. Диагональное сечение правильной четырехугольной призмы представляет собой прямоугольник

Перпендикулярное сечение (ортогональное сечение) – это пересечение призмы и плоскости, проведенной перпендикулярно ее боковым ребрам

Элементы правильной четырехугольной призмы

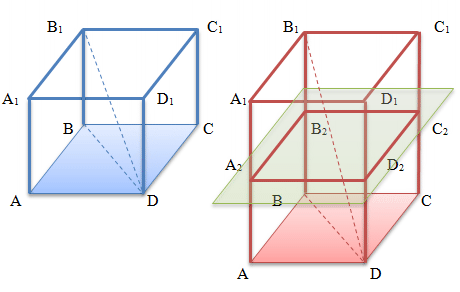
На рисунке изображены две правильные четырехугольные призмы, у которых обозначены соответствующими буквами:

Свойства правильной четырехугольной призмы

Формулы для правильной четырехугольной призмы

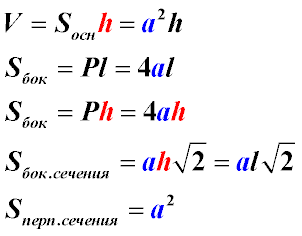
Указания к решению задач

При решении задач на тему “правильная четырехугольная призма” подразумевается, что:

Правильная призма — призма в основании которой лежит правильный многоугольник, а боковые ребра перпендикулярны плоскостям основания. То есть правильная четырехугольная призма содержит в своем основании квадрат. (см. выше свойства правильной четырехугольной призмы)

Примечание. Это часть урока с задачами по геометрии (раздел стереометрия –  призма). Здесь размещены задачи, которые вызывают трудности при решении. Если Вам необходимо решить задачу по геометрии, которой здесь нет – пишите об этом в форуме. Для обозначения действия извлечения квадратного корня в решениях задач используется символ √ .   

15306.1214
 

 Прямая призма |

Описание курса

| Куб