({color{red}{{small{textbf{Факт 1. Про шаровой сегмент}}}}})
(bullet) Шаровой сегмент – шасть шара, отсекаемая от него плоскостью ((alpha)).
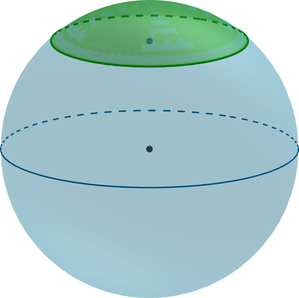
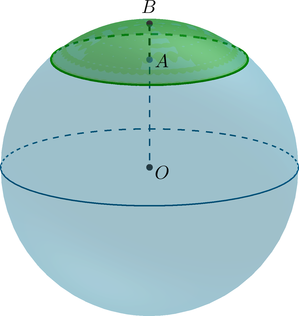
(bullet) Если (O) – центр шара, (OB=R) – радиус шара, перпендикулярный плоскости (alpha), (A) – центр круга (основания шарового сегмента), а также точка пересечения радиуса (OB) c этим кругом, то
(H=AB) – высота шарового сегмента.
(bullet) Площадь сферического сегмента (часть сферы, отсекаемая от нее плоскостью (alpha)) вычисляется по формуле [S=2pi cdot RH] (bullet) Объем шарового сегмента вычисляется по формуле [V=pi H^2cdot left(R-frac13Hright)]
({color{red}{{small{textbf{Факт 2. Про шаровой слой}}}}})
(bullet) Шаровой слой – часть шара, ограниченная двумя параллельными плоскостями, пересекающими шар.
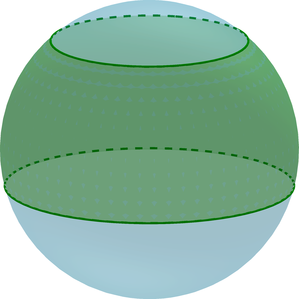
(bullet) Основания шарового слоя – это сечения шара плоскостями.
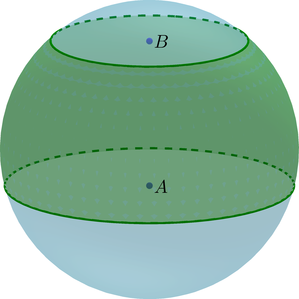
(bullet) Высота (H=AB) шарового слоя – это расстояние между основаниями.
(bullet) Площадь сферической части шарового слоя равна [S=2pi RH] где (R) – радиус шара.
(bullet) Объем шарового слоя равен разности объемов двух шаровых сегментов: [V=V_{A}-V_{B}]
({color{red}{{small{textbf{Факт 3. Про шаровой сектор}}}}})
(bullet) Шаровой сектор – часть шара, ограниченная сферической частью шарового сегмента и боковой поверхностью конуса, имеющего то же основание, что и шаровой сегмент.
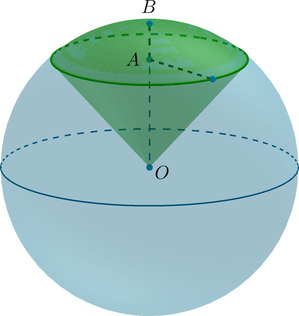
(bullet) Если (H=AB), то объем шарового сектора равен [V=dfrac23pi R^2cdot H]
Как найти объем шарового сегмента?
Шаровой сектор — это часть шара, ограниченная кривой поверхностью шарового сегмента и конической поверхностью, основанием которой служит основание сегмента, а вершиной — центр шара. Формула объема шарового сектора: V = (2/3)*πR²*h, где h – высота сегмента.
Что такое шаровой сегмент?
Шаровым сегментом называется часть шара, отсекаемая от него плоскостью. Рисуется большой круг. Круг с центром A — основание шарового сегмента.
Как вычислить объем шара формула?
Формула для вычисления объема шара Объем шара равен четырем третим от его радиуса в кубе помноженого на число пи. где V – объем шара, R – радиус шара, π = 3.
Как найти высоту сегмента шара?
S=πR(2h+r), где h − высота соответствующего шарового сегмента, r − радиус основания шарового сегмента (или конуса), R − радиус шара.
Как найти хорду в окружности?
Формула длины хорды окружности
- α = градус
- α = радиан
- α = x / радиан
Как найти сегмент круга?
Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой. P=s+a, где s − длина дуги, a − длина хорды.
Как вычислить площадь сегмента круга?
Площадь сегмента круга
- α = градус
- α = радиан
- α = x / радиан
Как вычислить окружность круга?
Диаметр круга рассчитывается по следующим формулам:
- Если нам известна длина: Формула для расчета диаметра круга через его длину: D=P/π
- Если нам известна площадь: Формула для расчета диаметр круга через площадь: D=2√S/π
- Если нам известен диаметр: Формула для расчета диаметр круга через радиус: D=2R.
Что такое круговой сегмент как можно вычислить его площадь?
Можно воспользоваться приближенной формулой вычисления площади кругового сегмента: S=2/3*(a*h), где a – основание треугольника или длина хорды, h – высота сегмента, которая является результатом разности между радиусом круга и высотой равнобедренного треугольника. … Как правило, за основу берется треугольник.
Как найти площадь сегмента формула?
Площадь сегмента можно найти как разность площадей сектора круга и этого равнобедренного треугольника.
Что такое круговой сегмент?
Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).
Что такое сегмент в математике?
Сегмент — (от лат. segmentum отрезок, полоса, от seco режу, рассекаю) часть чего либо. В математике Сегмент, или отрезок множество точек прямой, включающее свои концы.
Что такое сегмент в биологии?
Сегмент (биология) — части тела, похожие по строению и расположенные последовательно вдоль продольной оси тела.
Что такое сегмент по анатомии?
segmentum — «отрезок») — анатомический комплекс, состоящий из двух смежных позвонков с соответствующими суставами и мышечно-связочным аппаратом на этом уровне, и одного межпозвонкового диска между этими позвонками. травматологии, мануальной терапии, рентгенологии и др. специальностях медицины.
Что означает слово сегмент?
Сегмент, или отрезок — множество точек прямой, включающее свои концы. Сегмент (геометрия) — плоская фигура, заключённая между кривой и её хордой. Сегмент (стереометрия) — часть тела, ограниченная плоскостью и отсекаемой ею частью поверхности. Как частный случай: шаровой сегмент.
Что такое сегментация целевой аудитории?
Сегментирование целевой аудитории – это разделение аудитории на группы, где они объединены по признаку схожих потребностей (запросов).
Что такое сегмент в бизнесе?
Область рынка, в которой компания имеет возможность занять лидирующие позиции. Бизнес–сегмент — область деятельности, направление специализации компании, в котором она получает и наращивает конкурентные преимущества.
Что такое сектор и сегмент?
Определение. Сектор (◔) – часть круга, которая ограничена двумя радиусами и дугой между этими радиусами. Определение. Сегмент – часть круга, которая ограничена дугой и хордой, что соединяет ее концы.
Что называется сектором?
Сектор круга — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Что такое сектор в информатике?
Се́ктор диска — минимальная адресуемая единица хранения информации на дисковых запоминающих устройствах (НЖМД, дискета, CD). Является частью дорожки диска. Первоначально у большинства устройств размер сектора составляет 512 байт (например, у жестких и гибких дисков), либо 2048 байт (например, у оптических дисков).
Что такое кластер на компьютере?
Кластер (англ. cluster) — в некоторых типах файловых систем – логическая единица хранения данных в таблице размещения файлов, объединяющая группу секторов. … Как правило, это наименьшее место на диске, которое может быть выделено для хранения файла.
Что такое сектор дорожка и кластер магнитного диска?
Сектор диска — минимальная адресуемая единица хранения информации на дисковых запоминающих устройствах (НЖМД, дискета, CD). Является частью дорожки диска. В случае FAT16 для диска объемом 512 Мб кластер будет составлять 8 Кб, до 1 Гб — 16 Кб, до 2 Гб — 32 Кб и так далее. …
Что такое кластер по литературе?
Кластер — это графическая форма организации информации, когда выделяются основные смысловые единицы, которые фиксируются в виде схемы с обозначением всех связей между ними. Он представляет собой изображение, способствующее систематизации и обобщению учебного материала.
Что такое цилиндр на жестком диске?
Цили́ндр у дискового накопителя — совокупность всех дорожек в заданном положении привода. В каждой позиции привода жёсткого диска каждая из головок может считывать свою дорожку (участок поверхности пластины в виде кольца).
Что такое дисковый накопитель?
Накопи́тель на жёстких магни́тных ди́сках, или НЖМД (англ. hard (magnetic) disk drive, HDD, HMDD), жёсткий диск, разг. винчестер — запоминающее устройство (устройство хранения информации, накопитель) произвольного доступа, основанное на принципе магнитной записи.
Сколько секторов в одной дорожке в адресации CHS?
Затем контроллеры стали сообщать, будто в дорожке 63 сектора, а на одной поверхности диска 255 дорожек (максимально допустимые значения), число же головок подбирается сообразно объёму.
Как определяется физический адрес сектора?
Информация на магнитных дисках размещается и передается блоками, которые называются секторами. … Физический адрес сектора на диске определяется триадой [c-h-s], где c – номер цилиндра (cylinder), h – номер рабочей поверхности диска (магнитной головки, head), s – номер сектора на дорожке (sector).
В данной публикации мы рассмотрим формулу, с помощью которой можно вычислить объем сектора шара, а также пример решения задачи для демонстрации ее применения на практике.
-
Определение сектора шара
- Формула для нахождения объема сектора шара
- Пример задачи
Определение сектора шара
Сектор шара (или шаровый сектор) – это часть шара, состоящая из шарового сегмента и конуса, вершиной которого является центр шара, а основанием – основание соответствующего сегмента. На рисунке ниже сектор закрашен оранжевым цветом.

- R – радиус шара;
- r – радиус основания сегмента и конуса;
- h – высота сегмента; перпендикуляр от центра основания сегмента до точки на сфере.
Формула для нахождения объема сектора шара
Чтобы найти объем шарового сектора, необходимо знать радиус шара и высоту соответствующего сегмента.
![]()
Примечания:
- если вместо радиуса шара (R) дан его диаметр (d), последний следует разделить на два, чтобы найти требуемый радиус.
- π округленно равняется 3,14.
Пример задачи
Дан шар радиусом 12 см. Найдите объем шарового сектора, если высота сегмента, из которого состоит данный сектор, равняется 3 см.
Решение
Применим формулу, рассмотренную выше, подставив в нее известные по условиям задачи значения:
![]()
Шаровой сектор – это часть шара, ограниченная кривой поверхностью шарового сегмента и конической
поверхностью, основанием которой служит основание сегмента, а вершиной центр шара. Другое
определение исходит из того, что шаровой сектор – тело вращения, т.е. образовано вращением
какой-либо плоской и ограниченной кривой геометрической фигуры вокруг лежащей в той же плоскости
оси. Объем шарового сегмента определяется рядом его размеров, ниже 2 формулы для вычисления
объема.
- Обьём шарового сектора через радиус шара и высоту шарового
сегмента - Обьём шарового сектора через радиус шара и угол между осью
и образующей конуса
Объём шарового сектора через радиус шара и высоту шарового сегмента
Зная радиус и высоту шарового сектора, можно найти его объем по следующей формуле:
V = 2/3 * π * R² * h
где R – радиус шара, h – высота шарового сегмента (или проекция хорды, стягивающей дугу сектора, на
ось вращения).
Цифр после
запятой:
Результат в:
Значение π примерно равно 3,14 – это числовая постоянная «число пи», одна из самых известных и чаще
всего использующихся, равная отношению длины окружности к ее диаметру; для всех окружностей это
отношение постоянно. «Пи» число иррациональное и трансцендентное, т.е. не может быть выражено
никакой рациональной дробью и не может быть корнем какого-либо многочлена с целыми
коэффициентами.
Пример. Радиус R = 5 м; h = 1,5 м. Рассчитываем объем: V = 2 * π * R² * h / 3 = 2 * 3,14 * 5² * 1,5 / 3 = 78,5 м³.
Объём шарового сектора через радиус шара и угол между осью и образующей конуса
При известном радиусе шара и угла между осью и образующей конуса можно так же найти объем шарового
сектора. Для это применяется формула:
V = 2/3 * π * R³ * (1 — cos α/2)
где R – радиус шара, cos α – угол между осью и образующей конуса.
Цифр после
запятой:
Результат в:
Пример. Вафельный рожок для мороженого, при заполнении мороженым имеющий форму
шарового сектора, имеет такие размеры: радиус R = 11 см, угол α = 26°. Необходимо рассчитать объем
мороженого в рожке при его заполнении. V = 2/3 * 3,14 * 11³ * (1 — cos 26º/2) = 71 см³.
Шаровой сектор – это геометрическое тело, возникающее при вращении сектора вокруг одного из его
радиусов. Форму, близкую к шаровому сектору, имеют, в качестве примера, современные воздушные шары и
мороженое в вафельном рожке.
На этом уроке мы введём понятия шарового сегмента,
шарового слоя и шарового сектора. А также выведем формулы для вычисления их объёмов.
Прежде чем приступить к рассмотрению данной темы,
давайте вспомним, что такое шар.
Определение:
Итак, шар
– это совокупность всех точек пространства, находящихся от данной точки на
расстоянии, не больше данного. Причём, данная точка называется центром
шара, а данное расстояние – радиусом шара.
Самой простой фигурой, которую можно начертить,
используя шар, является шаровой сегмент.
Определение:
Шаровым сегментом
называется часть шара, отсекаемая от него какой-нибудь плоскостью.
На экране вы видите, как секущая плоскость ,
проходящая через точку ,
разделяет шар на два шаровых сегмента. Круг, получившийся в сечении, называется
основанием каждого из этих сегментов, а длины отрезков и
диаметра
,
перпендикулярного к секущей плоскости, называются высотами
сегментов.
Верно следующее утверждение: если радиус шара равен ,
а высота сегмента равна ,
то объем шарового
сегмента можно вычислить по формуле:
Докажем это утверждение. Доказывать
будем с помощью определённого интеграла.
Проведём ось перпендикулярно
к плоскости .
Тогда площадь ,
при .
Вычислим объём шарового сегмента с помощью основной
формулы объёма тела. Вспомним её: .
Итак, применим основную формулу для вычисления объёмов
тел получаем, что объём шарового сегмента равен .
Что и требовалось доказать.
Заметим, что если высоту в
формуле объема шарового сегмента заменить
на ,
то получим формулу для нахождения объёма шара:
А если заменить высоту на
радиус ,
то получим формулу для нахождения объёма полушара.
Кстати, в жизни нас также окружают некоторые объекты,
имеющие форму очень близкую к форме шарового сегмента.
В современной авиации наиболее популярны парашюты в
виде сегмента.
Форму шарового сегмента нередко используют и в
архитектуре, интерьере, декоре.
Перейдём к шаровому слою.
Определение:
Шаровым слоем
называется часть шара, заключённая между двумя параллельными секущими плоскостями.
На экране вы видите изображение шарового слоя.
Круги, получившиеся в сечении шара плоскостями,
называются основаниями шарового слоя, а расстояние между
плоскостями – высотой шарового слоя.
Нетрудно заметить, что объём шарового слоя можно
вычислить, как разность объёмов двух шаровых сегментов.
Объём шарового слоя, изображённого на экране, равен
разности объёмов шаровых сегментов, высоты которых равны и
.
Если высота шарового слоя равна ,
а радиусы и
–
радиусы оснований шарового слоя соответственно, то объем шарового слоя можно
вычислить по формуле:
Декоративная свеча может служить примером шарового
слоя в жизни.
И теперь перейдём к шаровому сектору.
Определение:
Шаровым сектором
называется тело, которое получается при вращении кругового сектора с углом,
меньшим 90о, вокруг прямой, содержащей один из ограничивающих круговой
сектор радиусов.
Обратите внимание, шаровой сектор состоит из шарового
сегмента и конуса. Причём шаровой сегмент имеет высоту ,
а конус высоту ,
где –
радиус шара.
Понятно, что шаровая поверхность пересекается с
конусом по окружности. Радиус этой окружности равен .
Если радиус шара равен ,
а высота шарового сегмента равна ,
то объем шарового
сектора можно найти по формуле:
Для того чтобы получить данную формулу необходимо
сложить объём конуса (с вершиной O), лежащего под плоскостью, и объём шарового сегмента,
лежащего над плоскостью.
Большой воздушный шар имеет форму близкую к форме
шарового сектора в жизни.
Перейдём к задачам.
Задача: радиус
шара равен см.
Вычислите объем шарового сегмента, если его высота равна см.
Решение: запишем
формулу для вычисления объёма шарового сегмента.
И подставим в неё радиус шара и высоту шарового
сегмента.
Запишем ответ.
Задача: по
разные стороны от центра шара проведены два параллельных сечения с площадью и
см2.
Расстояние между сечениями равно см.
Определите объём получившегося шарового слоя.
Решение: запишем
формулу для вычисления объема шарового слоя.
Чтобы найти объём шарового слоя нам необходимо знать
его высоту и радиусы двух его оснований.
По условию задачи нам дано расстояние между сечениями,
как раз-таки это расстояние и есть высота данного шарового слоя, и она равна .
Теперь найдём чему равны радиусы оснований шарового
слоя. Напомню, что сечением шара плоскостью является круг. Площадь круга
вычисляется по формуле .
Отсюда найдём радиусы оснований шарового слоя. Тогда имеем, радиус одного основания
равен (см),
радиус второго основания равен (см).
Подставим радиусы оснований и высоту шарового слоя в
формулу его объёма. Посчитаем. Получаем, что объём данного шарового слоя равен .
Не забудем записать ответ
Задача: радиус
шара равен см.
Найдите объем шарового сектора, если высота шарового сегмента равна см.
Решение: запишем
формулу для вычисления объёма шарового сектора.
Подставим в неё радиус шара и высоту шарового
сегмента. Посчитаем. Получим, что объём данного шарового сектора равен .
Запишем ответ.
Итоги:
На этом уроке мы ввели понятия шарового сегмента,
шарового слоя и шарового сектора. Узнали, что шаровым сегментом называется
часть шара, отсекаемая от него какой-нибудь плоскостью. Шаровым слоем
называется часть шара, заключённая между двумя параллельными секущими плоскостями.
Шаровым сектором называется тело, которое получается при вращении кругового
сектора с углом, меньшим 90о, вокруг прямой, содержащей один из ограничивающих
круговой сектор радиусов. А также вывели формулы для вычисления объёмов этих
тел.
