Как найти высоту трапеции зная если известен косинус угла основания и боковая сторона?
На этой странице сайта размещен вопрос Как найти высоту трапеции зная если известен косинус угла основания и боковая сторона? из категории
Геометрия с правильным ответом на него. Уровень сложности вопроса
соответствует знаниям учеников 5 – 9 классов. Здесь же находятся ответы по
заданному поиску, которые вы найдете с помощью автоматической системы.
Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по
заданной теме. На этой странице можно обсудить все варианты ответов с другими
пользователями сайта и получить от них наиболее полную подсказку.
Как вычислить высоту трапеции
Если в четырехугольнике только две противоположных стороны параллельны, его можно назвать трапецией. Пара непараллельных отрезков, образующих эту геометрическую фигуру, называется боковыми сторонами, а другая пара – основаниями. Расстояние между двумя основаниями определяет высоту трапеции и может быть рассчитано несколькими способами.
Инструкция
Если в условиях даны длины обоих оснований (a и b) и площадь (S) трапеции, начните вычисление высоты (h) с нахождения полусуммы длин параллельных сторон: (a+b)/2. Затем на полученное значение разделите площадь – результат и будет искомой величиной: h = S/((a+b)/2) = 2*S/(a+b).
Зная длину средней линии (m) и площадь (S) можно упростить формулу из предыдущего шага. По определению средняя линия трапеции равна полусумме ее оснований, поэтому для вычисления высоты (h) фигуры просто разделите площадь на длину средней линии: h = S/m.
Можно определить высоту (h) такого четырехугольника и в том случае, если даны только длина одной из боковых сторон (с) и угол (α), образуемый ей и длинным основанием. В этом случае следует рассмотреть треугольник, образуемый этой стороной, высотой и коротким отрезком основания, который отсекает опущенная на него высота. Этот треугольник будет прямоугольным, известная сторона будет в нем гипотенузой, а высота – катетом. Отношение длин катета и гипотенузы равно синусу противолежащего катету угла, поэтому для вычисления высоты трапеции умножьте известную длину стороны на синус известного угла: h = с*sin(α).
Такой же треугольник стоит рассмотреть и если даны длина боковой стороны (с) и величина угла (β) между ней и другим (коротким) основанием. В этом случае величина угла между боковой стороной (гипотенузой) и высотой (катетом) будет на 90° меньше известного из условий угла: β-90°. Так как отношение длин катета и гипотенузы равно косинусу угла между ними, то высоту трапеции вычислите умножением косинуса уменьшенного на 90° угла на длину боковой стороны: h = с*cos(β-90°).
Если в трапецию вписана окружность известного радиуса (r), формула вычисления высоты (h) будет очень проста и не потребует знания никаких других параметров. Такая окружность по определению должна касаться каждого из оснований только одной точкой и эти точки будут лежать на одной линии с центром круга. Это значит, что расстояние между ними будет равно диаметру (удвоенному радиусу), проведенному перпендикулярно основаниям, то есть совпадающим с высотой трапеции: h=2*r.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Как найти высоту трапеции зная если известен косинус угла основания и боковая сторона?
Найди верный ответ на вопрос ✅ «Как найти высоту трапеции зная если известен косинус угла основания и боковая сторона? …» по предмету 📙 Геометрия, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Новые вопросы по геометрии
Главная » Геометрия » Как найти высоту трапеции зная если известен косинус угла основания и боковая сторона?
Высота трапеции
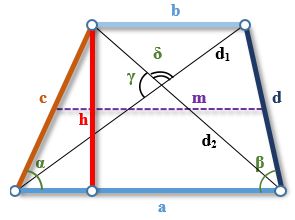
на рисунке обозначены:
a – большее основание трапеции
b – меньшее основание
c,d – боковые стороны трапеции
m – средняя линия трапеции
h – высота трапеции
d1, d2 – диагонали трапеции
α, β – углы между основанием и боковыми сторонами
γ, δ – углы между диагоналями трапеции
Формулы нахождения высоты трапеции
Высоту трапеции можно найти через длины ее сторон, диагоналей, углы между боковыми сторонами и основанием и углы между диагоналями. Также ее можно вычислить через площадь и среднюю линию трапеции:
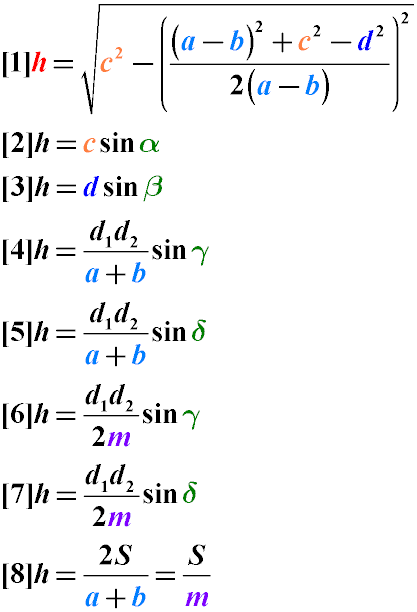
Высота трапеции равна произведению длины боковой стороны на синус угла между этой стороной и большим основанием трапеции. (Формулы 2 и 3)
Высоту трапеции можно найти как произведение длин диагоналей и синуса угла между ними, деленное на сумму длин оснований трапеции. (Формулы 4 и 5)
Высота трапеции равна произведению длин диагоналей и синуса угла между ними, деленными на удвоенную среднюю линию трапеции (Формулы 5 и 6)
Высоту трапеции можно вычислить как площадь такой трапеции деленную на длину ее средней линии (Формула 8)
0
Площадь трапеции |
Описание курса
| Трапеция (задачи про основания)
