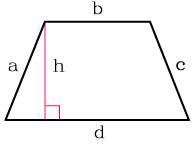
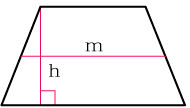
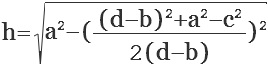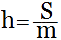Трапеция представляет собой уникальную по своей простоте фигуру, состоящую из прямоугольника и двух присоединенных к нему прямоугольных треугольников. Стороной всех этих фигур внутри трапеции является высота, проведенная из углов при верхнем основании. Высота трапеции открывает множество вероятных решений для любых задач, и найти ее можно несколькими способами. Зная площадь трапеции и ее среднюю линию (или два основания, среднее арифметическое которых дает среднюю линию), можно вычислить высоту трапеции, разделив одно на другое:
Более изощренным является вычисление высоты трапеции через все ее стороны. В данном случае помимо высоты в трапеции нужно провести также диагональ, которая сформирует прямоугольный треугольник и даст возможность выразить высоты несколькими разными способами через разные треугольники.
Выразив все стороны треугольников через стороны трапеции и приведя подобные слагаемые, получается следующая формула:
/
/
/ Высота трапеции
Высота трапеции
Установить Высота трапеции на мобильный
Найти высоту трапеции
зная стороны
|
||
| Основание трапеции a | ||
| Основание трапеции b | ||
| Сторона трапеции c | ||
| Сторона трапеции d | ||
|
|
||
| Высота трапеции h |
Вычислить высоту трапеции
через среднюю линию и площадь
|
||
| Средняя линия трапеции m | ||
| Площадь трапеции S | ||
| Высота трапеции h |
Скачать калькулятор
Рейтинг: 2.8 (Голосов 18)
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»
Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»
Сообщить об ошибке
Смотрите также
| Высота треугольника | Высота равнобедренного треугольника | Высота пирамиды | Высота ромба |
| Высота параллелограмма | Высота равностороннего треугольника | Высота цилиндра |
Трапецией принято называть выпуклую четырёхугольную четырехугольник с парой параллельных и двумя не
параллельными сторонами. Отрезки, которые создают параллельные прямы называются «основанием
трапеции», две других стороны играют роль «боковой стороны трапеции». Средняя линия трапеции будет
соединять два центра боковых сторон.
- Высота трапеции через боковую сторону и прилегающий угол
при основании - Высота трапеции через площадь и длины оснований
- Высота трапеции через площадь и среднию линию
- Высота трапеции через основании, диагонали и угол между
диагоналями - Высота трапеции через среднию линию, диагонали и угол между
диагоналями
Как найти высоту при помощи боковой стороны и прилегающего угла при основании
Для вычисления высоты трапеции через боковую сторону и прилегающий угол при основании нужно
воспользоваться нижеприведенной формулой:
h = a · sin α
где h — это искомая высота трапеции, a — известная боковая сторона, sin α — угол
при основании.
Цифр после
запятой:
Результат в:
Пример. Чтобы разобраться с применением формулы, давайте рассмотрим пример. Дана
некая трапеция. Нам известно, что боковая сторона равна 10 сантиметрам, а прилегающих угол
составляет 30 гр. Нам нужно найти высоту данной трапеции. Для решения у нас есть вся нужная
информация и формула выше. Подставляем значения в формулу: h = a · sin, h = 10 · sin 30, h = 10 · 1/2, h = 5 см
Как найти высоту трапецию при помощи длины основания и площади трапеции
Чтобы найти высоту трапеции через известные длины основания и площадь, нужно воспользоваться
формулой:
h = (2S) / (a + b)
где h — это искомая высота трапеции, S — известная площадь фигуры, a и b — длины
обеих оснований.
Цифр после
запятой:
Результат в:
Пример. Закрепим на примере: Нам известно, что в трапеции АВСD основания a и b равны
5 и 10 сантиметров. Площадь фигуры равна 30 квадратных сантиметров. Для решения нужно
воспользоваться формулой. h = (2S) / (a + b), h = (2 х 30) / (5 + 10), h = 60 /15, h = 4 см.
Высота трапеции равна 4 см.
Как найти высоту при помощи диагоналей, углу между диагоналями и средней линией трапеции
Чтобы найти высоту трапеции через среднюю линию, известные диагонали и угол между ними, нужно
прибегнуть к применению выведенной формулы:
h = ((D x d) / (2m)) x sin (α)
где h — это искомая высота трапеции, D и d — известные диагонали, m — средняя
линия, sin(α) — угол между диагоналями.
Цифр после
запятой:
Результат в:
Пример. Закрепим на примере: Дана трапеция с диагоналями 5 и 12 сантиметров.
Известно, что средняя линия фигуры равна 6 см, а угол между диагоналями – 30 градусов. Применив
формулу выше, мы сможем с легкостью найти высоту трапеции. h = ((D x d) / (2m)) x sin (α), h = ((5 x 12) / (2 х 6)) x sin (30), h = (60 /12) x 0.5, h = 2.5 см.
Высота трапеции равна 2.5 см.
Как найти высоту при помощи средней линии и площади трапеции
Чтобы найти высоту трапеции через площадь и среднюю линию воспользуемся выведенной формулой:
h = (2S) / m
где h — это искомая высота трапеции, S — известная площадь фигуры, а m — средняя
линия.
Цифр после
запятой:
Результат в:
Пример. Закрепим на примере: Площадь произвольной трапеции составляет 30 квадратных
сантиметров. Средняя линия фигуры равна 5 см. Нужно найти высоту по формуле. h = (2S) / m, h = (2 х 30) / 5, h = 60 / 5, h = 12 см. 12
см – высота трапеции.
Как найти высоту при помощи известного основания, диагоналей трапеции и угла между диагоналями
Для нахождения высоты трапеции при помощи известного основания, диагонали и углу между диагоналями
используют нижеприведенную формулу:
h = ((Dd) / (a + b)) x sin (α)
где h — это искомая высота трапеции, D и d — известные диагонали, a и b — длины
обеих оснований, sin(α) — угол между диагоналями.
Цифр после
запятой:
Результат в:
Пример. Закрепим на примере: В трапеции ABCD диагонали равны 10 см каждая. Известно,
что сумма основ фигура равна 20 см. Угол, созданный между диагоналями – 30 градусов. Нужно найти
высоту. Для этого нужно воспользоваться выше предоставленной формулой. h = ((Dd) / (a+b)) x sin (α), h = ((10 х 10) / (20)) x sin (30), h = 5 x sin (30), h = 2.5 см.
Высота трапеции равна 2.5 см
Можно выделить 2 разновидности трапеции:
- Трапеция, в которой одна из боковых сторон лежит под перпендикулярным углом с обеими основами
называется прямоугольной. - Трапеции с равными боковыми сторонами называется равнобедренной.
Высотой трапеции принято называть отрезок, которой показывает самое короткое расстояние между верхним
и нижним основанием фигуры. Существует большое количество математических задач разного уровня
сложности, для решения которых активно применяют высоту. Стоит разобраться со всеми возможными
формулами, которые используются для нахождения высоты трапеции.
Высота трапеции Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Длинная нога трапеции: 11 метр –> 11 метр Конверсия не требуется
Длинное основание трапеции: 15 метр –> 15 метр Конверсия не требуется
Короткое основание трапеции: 5 метр –> 5 метр Конверсия не требуется
Короткая нога трапеции: 9 метр –> 9 метр Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
8.48528137423857 метр –> Конверсия не требуется
11 Высота трапеции Калькуляторы
5 Высота трапеции Калькуляторы
Высота трапеции формула
Высота трапеции = sqrt(Длинная нога трапеции^2-(((Длинное основание трапеции–Короткое основание трапеции)^2+Длинная нога трапеции^2-Короткая нога трапеции^2)/(2*(Длинное основание трапеции–Короткое основание трапеции)))^2)
h = sqrt(LLong^2-(((BLong–BShort)^2+LLong^2-LShort^2)/(2*(BLong–BShort)))^2)
Что такое Трапеция?
Трапеция – это четырехугольник с одной парой противоположных и параллельных сторон. Пару параллельных сторон называют основаниями трапеции, а пару непараллельных ребер — катетами трапеции. Из четырех углов трапеция обычно имеет 2 острых угла и 2 тупых угла, которые являются попарно дополнительными углами.
Формулы трапеции
❓Инструкция
Калькулятор для нахождения площади, средней линии и высоты трапеции.
Как пользоваться:
Необходимо выбрать неизвестную величину трапеции Указать известные величины Получить ответ
Ответ возможно получить с этапами решения, если выставить галочку «Подробнее». Также, есть возможность указать точность ответа. То есть количество знаков после запятой.
Ограничения:
Числа на входе должны быть: Вещественными Больше 0, но не больше 100 000. С точностью не более 10 знаков после запятой.
📖 Теория
трапеция
Трапеция представляет собой 4-стороннюю плоскую форму с прямыми сторонами, у которой пара противоположных сторон параллельна (отмечены стрелками ниже):
Трапеция:
имеет пару параллельных сторон является равнобедренной, если боковые стороны равны и углы при основаниях попарно равны.
Площадь трапеции
Площадь трапеции равняется полусумме оснований, умноженную на высоту.
$$S = frac{a + b}{2} * h$$, где $$S$$ — площадь, $$a,b$$ — основания трапеции, $$h$$ — высота.
Периметр трапеции
Периметр является суммой длин всех сторон :
$$P = a + b + c + d$$, где $$P$$ — периметр, $$a,b,c,d$$ — стороны трапеции.
Медиана трапеции
Медиана (называемая также средней линией) представляет собой отрезок линии на полпути между двумя основаниями.
Средняя линия трапеции равняется полусумме оснований.
$$m = frac{a + b}{2}$$, где $$m$$ — средняя линия трапеции, $$a,b$$ — основания трапеции.
Посмотрев на формулу площади трапеции, а затем на формулу средней линии, мы легко можем заметить, что площадь трапеции также можно найти как среднюю линию, умноженную на высоту.
$$S = m * h$$
Высота трапеции
Высоту трапеции можно найти при известных площади и средней линии трапеции как:
$$h = frac{S}{m}$$, где $$h$$ — высота, $$S$$ — площадь, $$m$$ — средняя линия трапеции.
А также при известных площади и двух оснований трапеции следующим образом:
$$h = frac{2S}{a + b}$$, где $$h$$ — высота, $$S$$ — площадь, $$a,b$$ — основания трапеции.
Последняя формула опять же вытекает из формулы средней линии трапеции.
➕ Примеры
Пример 1: Две стороны трапеции имеют длину 6 м и 4 м и высоту 3 м. Какова его площадь?
$$S = frac{6 м + 4 м}{2} * 3 м = 5 м * 3 м = 15 м^2$$.
Пример 2: Трапеция имеет длины сторон 5 см, 12 см, 4 см и 15 см, каков ее периметр?
$$P = a + b + c + d = 5 см + 12 см + 4 см + 15 см = 36 см$$.
Пример 3: Найдите высоту трапеции, если площадь трапеции равна $$28 см^2$$, а сумма длин оснований равна 14 см.
Способ 1: Воспользуемся формулой $$h = frac{S}{m}$$, нам известна площадь $$S = 28 см^2$$, а также сказано, что сумма длин оснований равна 14 см. То есть $$a + b = 14см$$.
Найдем среднюю линию $$m$$ по формуле $$m = frac{a + b}{2} = frac{14}{2} = 7см$$
А значит, $$h = frac{S}{m} = frac{28см^2}{7см} = 4см$$
Способ 2: Воспользуемся второй формулой (см. раздел теория)
$$h = frac{2S}{a + b}$$, нам дано $$S = 28 см^2$$ и $$a + b = 14см$$
подставляем в формулу.
$$h = frac{2 * 28 см^2}{14 см} = frac{56 см^2}{14 см} = 4 см$$.
