Высота трапеции как найти по теореме пифагора

Нахождение высоты по площади и основаниям

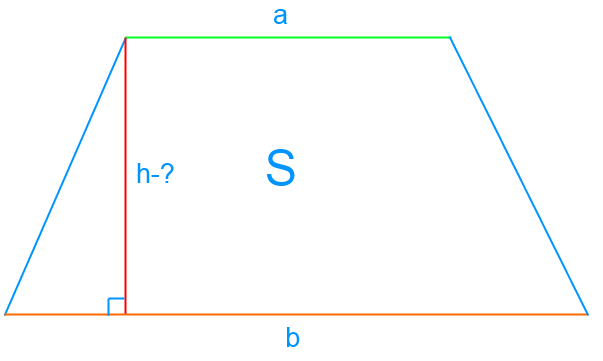
Чтобы вычислить площадь S трапеции мы используем формулу:

[S=frac{((a+b) times h)}{2}]

Здесь h — высота трапеции, а сегменты a и b являются ее основаниями.

Можем найти h:

[h=frac{2 times S}{(a+b)}]

Нахождение высоты, зная площадь и среднюю линию

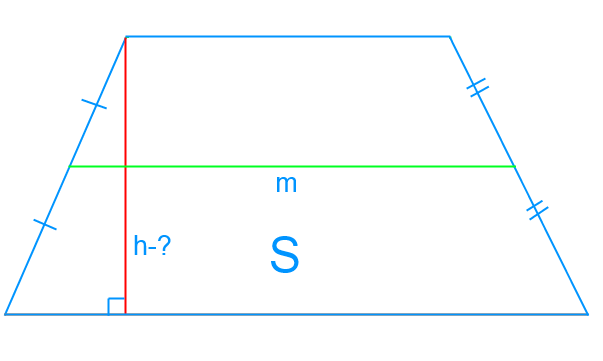
Мы используем формулу, с помощью которой можно рассчитать площадь трапеции:

S = m × h,   

Здесь h — это высота трапеции, m — ее средняя линия.

Можем найти h:

[h=frac{S}{m}], будет ответом.

Высота прямоугольной трапеции

Трапецию, одна из боковых сторон которой перпендикулярна основаниям, называют прямоугольной трапецией.

Таким образом, рассмотрим подобную трапецию ABCD, где AD — высота, AC — диагональ, DC-основание. Мы используем теорему Пифагора, которая говорит, что в прямоугольном треугольнике ADC квадрат гипотенузы AC равен сумме квадратов его сторон — катетов AB и BC.

Тогда мы сможем написать:

AC² = AD² + DC².

AD — это катет треугольника, сторона трапеции и, одновременно, ее высота. Так как отрезок перпендикулярен основаниям. Длина катета будет находиться как:

[A D=sqrt{left(A C^{2}-D C^{2}right)}]

Таким образом, у нас есть формула, которая поможет при вычислении найти высоту трапеции AD.

Нахождение высоты через стороны

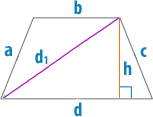
Существует еще один способ найти высоту — через стороны. Помимо высоты в трапеции стоит провести также ее диагональ, которая образует треугольник с прямым углом и даст возможность найти высоты несколькими различными способами через различные треугольники.

Если выразить все длины сторон таких треугольников через стороны трапеции и привести подобные слагаемые, то получится следующая формула:

[mathrm{h}=sqrt{C^{2}-left(frac{(a-b)^{2}+e^{2} d^{2}}{2(a-b)}right)^{2}}]

Высота трапеции – это перпендикуляр, который опущен с вершины трапеции на её основание.

Для нахождения высоты трапеции можно использовать целый ряд различных способов.

Приведу некоторые из них.

---

Высота трапеции через площадь и основания

Если известна площадь трапеции S и её основания a и b, то высота трапеции определяется по формуле:

h = 2S / (a + b).

Эта формула выводится исходя из того, что площадь трапеции равна полусумме оснований умноженной на высоту.

Например:

Площадь трапеции S = 20 см., основания a и b равны 4 см. и 6 см.

Высота h = 2 * 20 / (4 + 6) = 4 см.

---

Высота трапеции через площадь и среднюю линию

По определению, средняя линия трапеции представляет собой полусумму её оснований.

l = (a + b) / 2.

Если S = h * l, то высоту трапеции можно будет найти по формуле:

h = S / l.

Например:

Площадь трапеции S = 30 см. и средняя линия l = 10 см.

Высота h = 30 / 10 = 3 см.

---

Высота трапеции через боковую сторону и угол

Если дан угол при основании α или β, то высота находится так:

h = c * sinα или h = d * sinβ.

Данные формулы применяются исходя из того, что в прямоугольном треугольнике катет (в нашем случае высота) равен произведению гипотенузы (боковой стороны трапеции) на синус противолежащего угла.

Например:

Боковая сторона трапеции c = 25 см. и прилежащий к ней угол α = 30°.

Высота h = 25 * sin30° = 25 * 0,5 = 12,5 см.

В данной публикации мы рассмотрим различные формулы, с помощью которых можно вычислить высоту прямоугольной трапеции.

Напомним, в прямоугольной трапеции одна из боковых сторон перпендикулярна ее основаниями, и потому одновременно является высотой фигуры.

Нахождение высоты прямоугольной трапеции

Через длины сторон

Зная длины обоих оснований и большей боковой стороны прямоугольной трапеции, можно найти ее высоту (или меньшую боковую сторону):

Данная формула следует из теоремы Пифагора. В данном случае высота h – это неизвестный катет прямоугольного треугольника, гипотенуза которого равняется d, а известный катет – разности оснований, т.е. (a-b).

Через основания и прилежащий угол

Если даны длины оснований и любой из прилежащих к ним острых углов, то вычислить высоту прямоугольной трапеции можно по формуле:

Через боковую сторону и прилежащий угол

Если известна длина боковой стороны прямоугольной трапеции и прилежащий к ней угол (любой), найти высоту фигуры удастся таким образом:

Примечание: с помощью этой формулы можно, в т.ч., доказать, что меньшая боковая сторона – это и есть высота трапеции:

Через диагонали и угол между ними

При условии, что известны длины оснований прямоугольной трапеции, диагонали и угол между ними, рассчитать высоту фигуры можно так:

Если вместо суммы оснований известна длина средней линии, то формула примет вид:

m – средняя линия, которая равна половине суммы оснований, т.е.m = ^(a+b)/₂.

Через площадь и основания

Если известна площадь прямоугольной трапеции и длина ее оснований (или средней линии), найти высоту можно таким образом:

Как найти высоту трапеции

Трапецией считается такой четырехугольник, у которого две стороны параллельны, а две другие нет. Высотой трапеции называется отрезок, проведенный перпендикулярно между двумя параллельными прямыми. В зависимости от исходных данных ее можно вычислить по-разному.

Вам понадобится

• Знание сторон, оснований, средней линии трапеции, а так же, опционально, ее площадь и/или периметр.

Инструкция

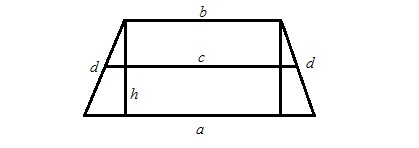
Одним из способов вычислить площадь трапеции является произведение высоты и средней линии. Допустим, что имеется равнобедренная трапеция. Тогда высота равнобедренной трапеции с основаниями a и b, площадью S и периметром P будет рассчитана так:

h=2 х S/(P-2 х d). (см. рис 1)

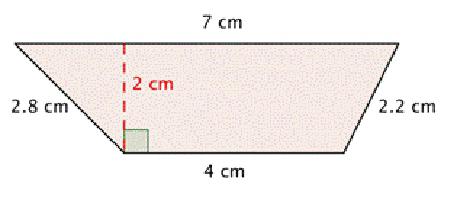
Если известна только площадь трапеции и ее основания, то формулу расчета высоты можно вывести из формулы площади трапеции S = 1/2h x (a+b):

h = 2S/(a+b).

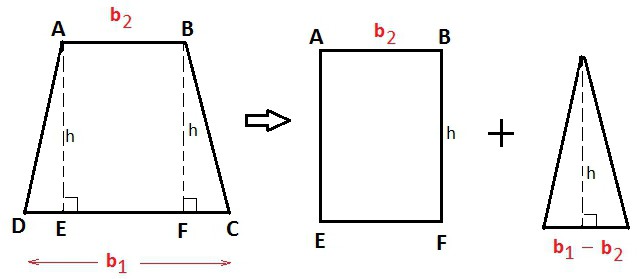
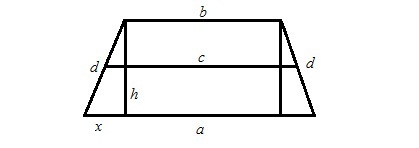
Допустим, имеется трапеция с теми же данными, что и на рисунке 1. Проведем 2 высоты, получим прямоугольник, у которого 2 меньшие стороны являются катетами прямоугольных треугольников. Обозначим меньший катит за x. Он находится путем деления разницы длин между большим и меньшим основаниями. Тогда по теореме Пифагора квадрат высоты равен сумме квадратов гипотенузы d и катета x. Извлекаем корень из этой суммы и получим высоту h. (рис. 2)

Видео по теме

Источники:

• как вычислить высоту трапеции

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

На простой вопрос «Как найти высоту трапеции?» существует несколько ответов, и все потому, что могут быть даны разные исходные величины. Поэтому и формулы будут различаться.

Эти формулы можно запомнить, но они несложно выводятся. Нужно только применять ранее изученные теоремы.

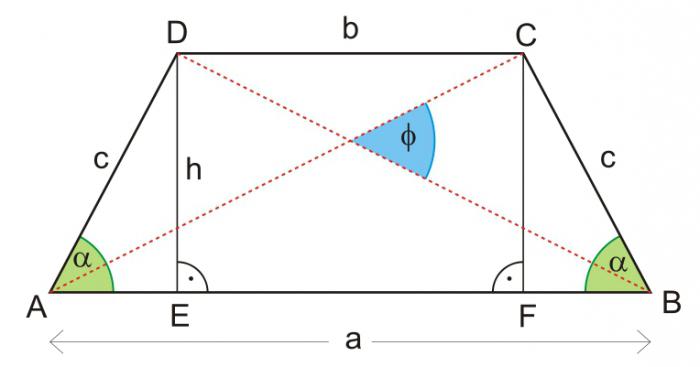
Принятые в формулах обозначения

Во всех приведенных ниже математических записях верны такие прочтения букв.

произвольная трапеция	равнобедренная трапеция	название
а	а	нижнее основание
в	в	верхнее основание
с, d	с	боковые стороны
н	н	высота
m	m	средняя линия
d1, d2	d1	диагонали
s	s	площадь
α, β	α	углы при нижнем основании
γ, δ	γ, δ	углы на пересечении диагоналей

В исходных данных: все стороны

Для того чтобы найти высоту трапеции в общем случае потребуется воспользоваться такой формулой:

н = √(с² – (((а – в)² + с² – d²)/(2(а – в)))²). Номер 1.

Не самая короткая, но и встречается в задачах достаточно редко. Обычно можно воспользоваться другими данными.

Формула, которая подскажет, как найти высоту равнобедренной трапеции в той же ситуации, гораздо короче:

н = √(с² – (а – в)²/4). Номер 2.

В задаче даны: боковые стороны и углы при нижнем основании

Принимают, что угол α прилежит к боковой стороне с обозначением «с», соответственно угол β к стороне d. Тогда формула для того, как найти высоту трапеции, в общем виде будет такой:

н = с * sin α= d * sin β. Номер 3.

Если фигура равнобедренная, то можно воспользоваться таким вариантом:

н = с * sin α= ((а – в) / 2) * tg α. Номер 4.

Известны: диагонали и углы между ними

Обычно к этим данным присоединяются еще известные величины. Например, основания или средняя линия. Если даны основания, то для ответа на вопрос, как найти высоту трапеции, пригодится такая формула:

н = (d₁* d₂ * sin γ) / (а + в) или н = (d₁* d₂ * sin δ) / (а + в). Номер 5.

Это для общего вида фигуры. Если дана равнобедренная, то запись преобразится так:

н = (d₁² * sin γ) / (а + в) или н = (d₁² * sin δ) / (а + в). Номер 6.

Когда в задаче идет речь о средней линии трапеции, то формулы для поиска ее высоты становятся такими:

н = (d₁* d₂ * sin γ) / 2m или н = (d₁* d₂ * sin δ) / 2m. Номер 5а.

н = (d₁² * sin γ) / 2m или н = (d₁² * sin δ) / 2m. Номер 6а.

Среди известных величин: площадь с основаниями или средней линией

Это, пожалуй, самые короткие и простые формулы того, как найти высоту трапеции. Для произвольной фигуры она будет такой:

н = 2S / (а + в). Номер 7.

Она же, но с известной средней линией:

н = S / m. Номер 7а.

Как ни странно, но для равнобедренной трапеции формулы будут выглядеть так же.

Задачи

№1. На определение углов при нижнем основании трапеции.

Условие. Дана равнобедренная трапеция, боковая сторона которой 5 см. Ее основания равны 6 и 12 см. Требуется найти синус острого угла.

Решение. Для удобства следует ввести обозначение. Пусть левая нижняя вершина будет А, все остальные по часовой стрелке: В, С, Д. Таким образом, нижнее основание будет обозначено АД, верхнее — ВС.

Нужно провести высоты из вершин В и С. Точки, которые укажут концы высот будут обозначены Н₁ и Н₂, соответственно. Поскольку в фигуре ВСН₁Н₂ все углы прямые, то она является прямоугольником. Это означает, что отрезок Н₁Н₂ равен 6 см.

Теперь нужно рассмотреть два треугольника. Они равны, так как являются прямоугольными с одинаковыми гипотенузами и вертикальными катетами. Отсюда следует, что и меньшие катеты у них равны. Поэтому их можно определить как частное от разности. Последняя получится от вычитания из нижнего основания верхнего. Делиться оно будет на 2. То есть 12 – 6 нужно поделить на 2. АН₁ = Н₂Д = 3 (см).

Теперь из теоремы Пифагора нужно найти высоту трапеции. Она необходима для нахождения синуса угла. ВН₁ = √(5² – 3²) = 4 (см).

Воспользовавшись знанием о том, как находится синус острого угла в треугольнике с прямым углом, можно записать такое выражение: sin α= ВН₁ / АВ = 0,8.

Ответ. Искомый синус равен 0,8.

№2. На нахождение высоты трапеции по известному тангенсу.

Условие. У равнобедренной трапеции нужно вычислить высоту. Известно, что ее основания равны 15 и 28 см. Дан тангенс острого угла: 11/13.

Решение. Обозначение вершин такое же, как в предыдущей задаче. Снова нужно провести две высоты из верхних углов. По аналогии с решением первой задачи нужно найти АН₁ = Н₂Д, которые определятся как разность 28 и 15, деленная на два. После подсчетов получается: 6,5 см.

Поскольку тангенс — это отношение двух катетов, то можно записать такое равенство: tg α= АН₁ / ВН₁. Причем это отношение равно 11/13 (по условию). Так как АН₁ известен, то можно вычислить высоту: ВН₁= (11 * 6,5) / 13. Простые расчеты дают результат в 5,5 см.

Ответ. Искомая высота равна 5,5 см.

№3. На вычисление высоты по известным диагоналям.

Условие. О трапеции известно, что ее диагонали равны 13 и 3 см. Нужно узнать ее высоту, если сумма оснований составляет 14 см.

Решение. Пусть обозначение фигуры будет таким же, как раньше. Предположим, что АС — меньшая диагональ. Из вершины С нужно провести искомую высоту и обозначить ее СН.

Теперь потребуется выполнить дополнительное построение. Из угла С нужно провести прямую, параллельную большей диагонали и найти точку ее пересечения с продолжением стороны АД. Это будет Д₁. Получилась новая трапеция, внутри которой начерчен треугольник АСД₁. Он-то и нужен для дальнейшего решения задачи.

Искомая высота окажется еще и ей же в треугольнике. Поэтому можно воспользоваться формулами, изученными в другой теме. Высота треугольника определяется как произведение числа 2 и площади, деленное на сторону, к которой она проведена. А сторона оказывается равна сумме оснований исходной трапеции. Это исходит из правила, по которому выполнено дополнительное построение.

В рассматриваемом треугольнике все стороны известны. Для удобства введем обозначения х = 3 см, у = 13 см, z = 14 см.

Теперь можно сосчитать площадь, воспользовавшись теоремой Герона. Полупериметр будет равен р = (х + у + z)/ 2 = (3 + 13 + 14) / 2 = 15 (см). Тогда формула для площади после подстановки значений будет выглядеть так: S = √(15 * (15 – 3) * (15 – 13) * (15 – 14)) = 6 √10 (см²).

Теперь нужно сосчитать высоту: н = (2 * 6 √10) / 14 = 6√10 / 7 (см).

Ответ. Высота равна 6√10 / 7 см.

№4. Для поиска высоты по сторонам.

Условие. Дана трапеция, три стороны которой равны 10 см, а четвертая 24 см. Нужно узнать ее высоту.

Решение. Поскольку фигура равнобедренная, то потребуется формула под номером 2. В нее нужно просто подставить все значения и сосчитать. Это будет выглядеть так:

н = √(10² – (10 – 24)²/4) = √51 (см).

Ответ. н = √51 см.