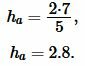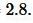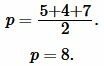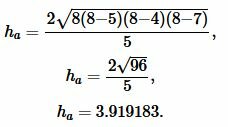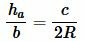Рассмотрим, как построить высоту треугольника с помощью чертежного угольника.
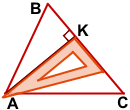
Чтобы построить высоту остроугольного треугольника, надо приложить угольник так, чтобы одна сторона прямого угла проходила через вершину треугольника, а вторая — через противоположную этой вершине сторону.
AK⊥BC.
AK — высота треугольника ABC, проведённая из вершины A к противолежащей стороне BC.
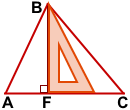
BF — высота треугольника ABC, опущенная из вершины B на сторону AC.
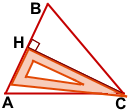
CH⊥AB.
CH — высота треугольника ABC, проведённая из вершины C к стороне AB.
Все высоты треугольника пересекаются в одной точке.
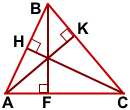
Если требуется построить все высоты треугольника, достаточно построить две, а третью провести из вершины треугольника через точку пересечения двух высот.
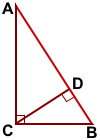
В прямоугольном треугольнике две стороны (катеты) являются также его высотами. Остаётся построить третью высоту.
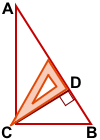
CD⊥AB.
CD — высота прямоугольного треугольника ABC, проведённая из вершины прямого угла C к гипотенузе AB.
Точка пересечения высот прямоугольного треугольника — вершина прямого угла.
Высоты AC, BC и CD прямоугольного треугольника ABC пересекаются в точке C, ∠C=90°.
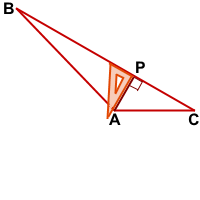
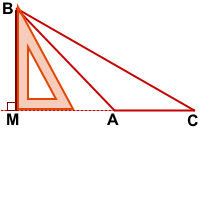
В тупоугольном треугольнике проще всего построить высоту, выходящую из вершины тупого угла.
Прикладываем угольник прямым углом так, чтобы одна его сторона проходила через наибольшую сторону треугольника, а другая — через тупой угол.
AP⊥BC.
AP — высота тупоугольного треугольника ABC, проведённая из вершины тупого угла A к стороне BC.
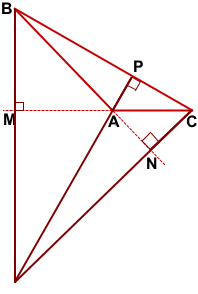
Только высота, проведённая из вершины тупого угла, лежит внутри треугольника. Две другие высоты находятся вне него.
Высоты тупоугольного треугольника, выходящие из вершин острых углов, проведены не к противолежащим сторонам, а к прямым, содержащим эти стороны.
Чтобы построить высоту, продлеваем противолежащую сторону и прикладываем угольник прямым углом таким образом, чтобы одна сторона угольника проходила через построенную прямую, а другая — через вершину острого угла.
BM⊥AC,
BM — высота тупоугольного треугольника ABC, проведённая из вершины острого угла B к прямой, содержащей противолежащую сторону AC.
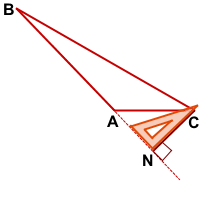
CN — высота тупоугольного треугольника ABC, проведённая из вершины острого угла С к прямой, содержащей противолежащую сторону AB.
Точка пересечения высот тупоугольного треугольника лежит вне него, за тупым углом, напротив наибольшей стороны.
Чтобы построить точку пересечения высот треугольника ABC, продлим прямые BM, CN и AP до пересечения.
Мы рассмотрели, как строить высоты треугольника с помощью угольника.
Построение высот с помощью циркуля и линейки будем рассматривать в теме «Задачи на построение».
Download Article
Download Article
To calculate the area of a triangle you need to know its height. To find the height follow these instructions. You must at least have a base to find the height.
-
1
Recall the formula for the area of a triangle. The formula for the area of a triangle is
A=1/2bh.
[1]
- A = Area of the triangle
- b = Length of the base of the triangle
- h = Height of the base of the triangle
-
2
Look at your triangle and determine which variables you know. You already know the area, so assign that value to A. You should also know the value of one side length; assign that value to “‘b'”.
Any side of a triangle can be the base,
regardless of how the triangle is drawn. To visualize this, just imagine rotating the triangle until the known side length is at the bottom.
Example
If you know that the area of a triangle is 20, and one side is 4, then:
A = 20 and b = 4.Advertisement
-
3
Plug your values into the equation A=1/2bh and do the math. First multiply the base (b) by 1/2, then divide the area (A) by the product. The resulting value will be the height of your triangle!
Example
20 = 1/2(4)h Plug the numbers into the equation.
20 = 2h Multiply 4 by 1/2.
10 = h Divide by 2 to find the value for height.
Advertisement
-
1
Recall the properties of an equilateral triangle. An equilateral triangle has three equal sides, and three equal angles that are each 60 degrees. If you
cut an equilateral triangle in half, you will end up with two congruent right triangles.
[2]
- In this example, we will be using an equilateral triangle with side lengths of 8.
-
2
Recall the Pythagorean Theorem. The Pythagorean Theorem states that for any right triangle with sides of length a and b, and hypotenuse of length c:
a2 + b2 = c2.
We can use this theorem to find the height of our equilateral triangle![3]
-
3
Break the equilateral triangle in half, and assign values to variables a, b, and c. The hypotenuse c will be equal to the original side length. Side a will be equal to 1/2 the side length, and side b is the height of the triangle that we need to solve.
- Using our example equilateral triangle with sides of 8, c = 8 and a = 4.
-
4
Plug the values into the Pythagorean Theorem and solve for b2.[4]
First square c and a by multiplying each number by itself. Then subtract a2 from c2.Example
42 + b2 = 82 Plug in the values for a and c.
16 + b2 = 64 Square a and c.
b2 = 48 Subtract a2 from c2. -
5
Find the square root of b2 to get the height of your triangle! Use the square root function on your calculator to find Sqrt(2. The answer is the height of your equilateral triangle!
- b = Sqrt (48) = 6.93
Advertisement
-
1
Determine what variables you know. The height of a triangle can be found if you have 2 sides and the angle in between them, or all three sides. We’ll call the sides of the triangle a, b, and c, and the angles, A, B, and C.
- If you have all three sides, you’ll use
Heron’s formula
, and the formula for the area of a triangle.
- If you have two sides and an angle, you’ll use the formula for the area given two angles and a side.
A = 1/2ab(sin C).[5]
- If you have all three sides, you’ll use
-
2
Use Heron’s formula if you have all three sides. Heron’s formula has two parts. First, you must find the variable
s, which is equal to half of the perimeter of the triangle.
This is done with this formula:
s = (a+b+c)/2.[6]
Heron’s Formula Example
For a triangle with sides a = 4, b = 3, and c = 5:
s = (4+3+5)/2
s = (12)/2
s = 6
Then use the second part of Heron’s formula, Area = sqr(s(s-a)(s-b)(s-c). Replace Area in the equation with its equivalent in the area formula: 1/2bh (or 1/2ah or 1/2ch).
Solve for h. For our example triangle this looks like:
1/2(3)h = sqr(6(6-4)(6-3)(6-5).
3/2h = sqr(6(2)(3)(1)
3/2h = sqr(36)
Use a calculator to calculate the square root, which in this case makes it 3/2h = 6.
Therefore, height is equal to 4, using side b as the base. -
3
Use the area given two sides and an angle formula if you have a side and an angle. Replace area in the formula with its equivalent in the area of a triangle formula: 1/2bh. This gives you a formula that looks like 1/2bh = 1/2ab(sin C). This can be simplified to
h = a(sin C)
, thereby eliminating one of the side variables.[7]
Note that angle C and side a are both positioned across from the height that you need to find (both on the right side from it, or both on the left side).Finding Height with 1 Side and 1 Angle Example
For example, with a = 3, and C = 40 degrees, the equation looks like this:
h = 3(sin 40)
Use your calculator to finish the equation, which makes h roughly 1.928.
Advertisement
Practice Problems and Answers
Add New Question
-
Question
How do I find the area of an equilateral triangle when only the height is given?
H = height, S = side, A = area, B = base. You know that each angle is 60 degrees because it is an equilateral triangle. If you look at one of the triangle halves, H/S = sin 60 degrees because S is the longest side (the hypotenuse) and H is across from the 60 degree angle, so now you can find S. The base of the triangle is S because all the sides are the same, so B = S. Using A = (1/2)*BH, you get A = (1/2)*SH, which you can now find.
-
Question
How do I calculate the height of a right triangle, given only the length of the base and the interior angle at the base?
Look up the tangent of the angle in a trigonometry table. Multiply the tangent by the length of the base.
-
Question
How do I determine the height of a triangle when I know the length of all three sides?
You already know the base, so calculate the area by Heron’s formula. Then, substitute the values you know in the formula. Area=1/2 * base * height or height=2 * Area/base and find your answer.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
References
About This Article
Article SummaryX
If you know the base and area of the triangle, you can divide the base by 2, then divide that by the area to find the height. To find the height of an equilateral triangle, use the Pythagorean Theorem, a^2 + b^2 = c^2. Cut the triangle in half down the middle, so that c is equal to the original side length, a equals half of the original side length, and b is the height. Plug a and c into the equation, squaring both of them. Then subtract a^2 from c^2 and take the square root of the difference to find the height. If you want to learn how to calculate the area if you only know the angles and sides, keep reading!
Did this summary help you?
Thanks to all authors for creating a page that has been read 2,406,243 times.
Reader Success Stories
-
“My Geometry teacher is not the best teacher, and I usually have to look up terms and lessons so I can teach myself…” more
Did this article help you?
В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту в различных видах треугольников, а также разберем примеры решения задач для закрепления материала.
-
Нахождение высоты треугольника
- Высота в разностороннем треугольнике
- Высота в равнобедренном треугольнике
-
Высота в прямоугольном треугольнике
- Высота в равностороннем треугольнике
- Примеры задач
Нахождение высоты треугольника
Напомним, высота треугольника – это отрезок, проведенный перпендикулярно из вершины фигуры к противоположной стороне.
Высота в разностороннем треугольнике
Высоту треугольника abc, проведенного к стороне a, можно найти по формулам ниже:
1. Через площадь и длину стороны
где S – площадь треугольника.
2. Через длины всех сторон
где p – это полупериметр треугольника, который рассчитывается так:
3. Через длину прилежащей стороны и синус угла
4. Через стороны и радиус описанной окружности
где R – радиус описанной окружности.
Высота в равнобедренном треугольнике
Длина высоты ha, опущенной на основание a равнобедренного треугольника, рассчитывается по формуле:
Высота в прямоугольном треугольнике
Высота, проведенная к гипотенузе, может быть найдена:
1. Через длины отрезков, образованных на гипотенузе
2. Через стороны треугольника
Примечание: две остальные высоты в прямоугольном треугольнике являются его катетами.
Высота в равностороннем треугольнике
Для равностороннего треугольника со стороной a формула расчета высоты выглядит следующим образом:
Примеры задач
Задача 1
Найдите высоту треугольника, проведенную из вершины B к стороне AC, если известно, что AB = 7 см, а угол BAC = 45°.
Решение
В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:
Задача 2
Найдите длину основания равнобедренного треугольника, если высота, проведенная к нему, равняется 3 см, а боковые стороны – 5 см.
Решение
Вывести формулу для нахождения длины основания можно из формулы расчета высоты в равнобедренном треугольнике:
Все формулы высоты треугольника
Высота– перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.
H – высота треугольника
a – сторона, основание
b, c – стороны
β , γ – углы при основании
p – полупериметр, p=(a+b+c)/2
R – радиус описанной окружности
S – площадь треугольника
Формула длины высоты через стороны, ( H ):
Формула длины высоты через сторону и угол, ( H ):
Формула длины высоты через сторону и площадь, ( H ):
Формула длины высоты через стороны и радиус, ( H ):
Формулы для нахождения высоты треугольника
В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту в различных видах треугольников, а также разберем примеры решения задач для закрепления материала.
Нахождение высоты треугольника
Напомним, высота треугольника – это отрезок, проведенный перпендикулярно из вершины фигуры к противоположной стороне.
Высота в разностороннем треугольнике
Высоту треугольника abc, проведенного к стороне a, можно найти по формулам ниже:
1. Через площадь и длину стороны
где S – площадь треугольника.
2. Через длины всех сторон
где p – это полупериметр треугольника, который рассчитывается так:
3. Через длину прилежащей стороны и синус угла
4. Через стороны и радиус описанной окружности
где R – радиус описанной окружности.
Высота в равнобедренном треугольнике
Длина высоты ha, опущенной на основание a равнобедренного треугольника, рассчитывается по формуле:
Высота в прямоугольном треугольнике
Высота, проведенная к гипотенузе, может быть найдена:
1. Через длины отрезков, образованных на гипотенузе
2. Через стороны треугольника
Примечание: две остальные высоты в прямоугольном треугольнике являются его катетами.
Высота в равностороннем треугольнике
Для равностороннего треугольника со стороной a формула расчета высоты выглядит следующим образом:
Примеры задач
Задача 1
Найдите высоту треугольника, проведенную из вершины B к стороне AC, если известно, что AB = 7 см, а угол BAC = 45°.
Решение
В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:
Задача 2
Найдите длину основания равнобедренного треугольника, если высота, проведенная к нему, равняется 3 см, а боковые стороны – 5 см.
Решение
Вывести формулу для нахождения длины основания можно из формулы расчета высоты в равнобедренном треугольнике:
Высота треугольника онлайн
С помощю этого онлайн калькулятора можно найти высоту треугольника. Для нахождения высоты треугольника введите известные элементы треугольника и нажмите на кнопку “Вычислить”. Теоретическую часть смотрите ниже.
Открыть онлайн калькулятор
Высота треугольника. Определение
Определение 1. Отрезок, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.
Высота треугольника может содержаться внутри треугольника (Рис.1), совпадать со стороной треугольника (при прямоугольном треугольнике высота совпадает с катетом (Рис.2) ), проходить вне треугольника (при тупоугольном треугольнике(Рис.3)).
Теорема о пересечении высот треугольника
Теорема 1. Все три высоты треугольника (или их продолжения) пересекаются в одной точке.
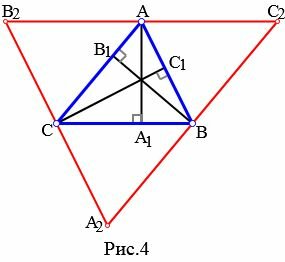
Доказательство. Рассмотрим произвольный треугольник ABC (Рис.4). Докажем, что высоты ( small AA_1 ,) ( small BB_1 ,) ( small CC_1 ) пересекаются в одной точке. Из каждой вершины треугольника проведем прямую, параллельно противоположной стороне. Получим треугольник ( small A_2B_2C_2. ) Покажем, что точки ( small A, B, C ) являются серединами сторон треугольника ( small A_2B_2C_2. ) ( small AB=A_2C ) так как они являются противоположными сторонами параллелограмма ( small ABA_2C. ) ( small AB=CB_2 ) так как они являются противоположными сторонами параллелограмма ( small ABCB_2. ) Тогда ( small CB_2=CA_2, ) то есть точка ( small C ) является серединой стороны ( small A_2B_2 ) треугольника ( small A_2B_2C_2. ) Аналогично доказывается, что точки ( small A ) и ( small B ) являются серединами сторон ( small B_2C_2 ) и ( small A_2C_2, ) соответственно.
Далее из ( small AA_1⊥BC ) следует, что ( small AA_1⊥B_2C_2 ) поскольку ( small BC ǁ B_2C_2 ). Аналогично, ( small BB_1⊥A_2C_2, ) ( small CC_1⊥A_2B_2. ) Получили, что ( small AA_1,) ( small BB_1, ) ( small CC_1) являются серединными перпендикулярами сторон ( small B_2C_2, ) ( small A_2C_2, ) ( small A_2B_2, ) соответственно. Но серединные перпендикуляры треугольника пересекаются в одной точке (см. статью Серединные перпендикуляры к сторонам треугольника). Следовательно высоты треугольника или их продолжения пересекаются в одной точке.
Точка пересечения высот треугольника называется ортоцентром.
Высота треугольника по основанию и площади
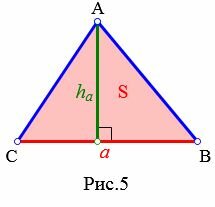
Пусть известны сторона треугольника и площадь. Найти высоту треугольника, отпущенная на известную сторону (Рис.5).
Решение. Площадь треугольника по основанию и высоте вычисляется из формулы:
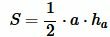
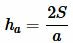 . . |
(1) |
Пример 1. Сторона треугольника равна ( small a=5 ) а площадь ( small S=7. ) Найти высоту треугольника.
Применим формулу (1). Подставляя значения ( small a ) и ( small S ) в (1), получим:
Ответ:
Высота треугольника по трем сторонам
Формула площади треугольника по трем сторонам имеет следующий вид (см. статью на странице Площадь треугольника онлайн):
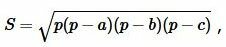 |
(2) |
где ( small a, b, c ) стороны треугольника а полупериод ( small p ) вычисляется из формулы:
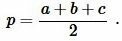 |
(3) |
Высота треугольника, отпущенная на сторону ( small a) вычисляется из формулы (1). Подставляя (2) в (1), получим формулу вычисления высоты треугольника по трем сторонам:
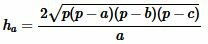 . . |
(4) |
Пример 2. Известны стороны треугольника: ( small a=5, ) ( small b= 4, ) ( small c=7. ) Найти высоту треугольника, отпущенная на сторону ( small a. )
Решение: Найдем, сначала полупериод ( small p ) треугольника из формулы (3):
Подставляя значения ( small a , b, c ) и ( small p ) в (4), получим:
Ответ:
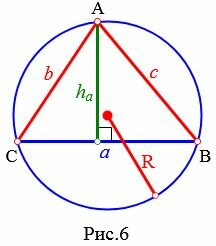
Высота треугольника по двум сторонам и радиусу описанной окружности
Рассмотрим треугольник на рисунке 6. Из теоремы синусов имеем:
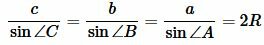 |
(5) |
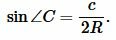 |
(6) |
Далее, из теоремы синусов имеем:
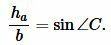 |
(7) |
Подставляя (6) в (7), получим:
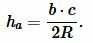 |
(8) |
Отметим, что радиус описанной окружности должен удовлетворять следующему неравенству:
(small max (b,c) ≤2R Пример 3. Известны стороны треугольника: ( small b=7, ) ( small c= 3 ) и радиус описанной окружности ( small R=4. ) Найти высоту треугольника, отпущенная на сторону ( small a. )
Решение: Проверим сначала условие (9):
(small max (7,3) ≤2 cdot 4 Ответ: ( small 2frac<5><8>. )
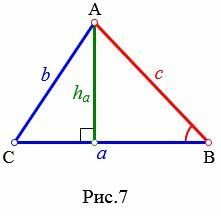
Высота треугольника по стороне и прилежащему к ней углу
Найдем высоту ( small h_a ) треугольника на рисунке 7. Из теоремы синусов имеем:
( small frac<large h_a><large sin angle B>=frac<large c><large sin 90°>, )
| ( small h_a=c cdot sin angle B. ) | (11) |
Пример 4. Известны сторона ( small c=12 ) треугольника и прилежащий угол ( small angle B=30°. ) Найти высоту треугольника, отпущенная на сторону ( small a. )
Решение: Для нахождения высоты треугольника подставим значения ( small c=12 ) и ( small angle B=30° ) в (11). Имеем:
[spoiler title=”источники:”]
http://matworld.ru/geometry/vysota-treugolnika.php
[/spoiler]
Как провести высоту треугольника
Решение геометрических задачек часто пригождается в повседневной жизни, а потому не грех вспомнить некоторые простые вещи, например, как найти высоту треугольника
Инструкция
Высота треугольника – это перпендикуляр, который был опущен из любой вершины треугольника на прямо противоположную сторону. А сторона, на которую опустили перпендикуляр – основание треугольника.
В тупоугольном треугольнике две его высоты лежат снаружи треугольника, и только третья высота находится внутри треугольника.
В треугольнике с острыми углами все его высоты расположены внутри треугольника.
В треугольнике прямоугольном катеты являются высотами треугольника.
Свойства высоты треугольника:
• Все три высоты в итоге неизменно пересекаются в одной точке, которая имеет название – Ортоцентр.
• В прямоугольном треугольнике высотой является перпендикуляр, который проведен из вершины прямого угла
• Основания высот образуют ортотреугольник, он обладает собственными свойствами
Способ вычисления высоты зависит от вида треугольника, в котором находится искомая высота. Вычислить высоту треугольника можно через другие его стороны и углы.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.