Задача о теплице, входит в первые пять заданий огэ по математике, и является практико-ориентированной задачей. Сложность данной задачи заключается в том, что в 5 задании требуется найти приближенное значение арифметического квадратного корня, и попасть в интервал ответов.
Вот текст задачи:
По этому тексту, нужно ответить на 5 вопросов.
1) Какое наименьшее количество дуг, нужно нужно заказать, чтобы расстояние между соседними дугами было не более 70 см.
Из первого предложения текста задачи, мы узнаем, что длина теплицы составляет 6 метров. Поэтому, первым делом находим количество интервалов, между дугами.
Теперь найдем, сколько будет дуг. Количество дуг = количество интервалов +1 = 9+1 = 10 дуг. Ответ 10
2) Сколько упаковок плитки необходимо купить для дорожек между грядками, она продается в упаковках по 14 штук?
Для этого вопроса, информация в тексте задачи дана в последнем предложении “Между грядками будут дорожки шириной 50 см, для которых необходимо купить тротуарную плитку размером 25х25”
Поскольку у нас ширина дорожки 50 см, а ширина плитки 25 см, то в ширину дорожки можно уложить 2 плитки. Длина у нас 6 метров, что составляет 600 см, поэтому в длину уместится 24 плитки. Тогда во всей дорожке будет 48 плитки. а в двух дорожках 96 штук.
Расчет количества упаковок приведен ниже.
3) Найдите ширину теплицы. Ответ дайте в метрах до сотых.
Ширина теплицы – это отрезок АD. Поскольку теплица состоит из дуг, то АD- это диаметр окружности.
Диаметр окружности связан с длиной окружности следующей формулой:
В этой формуле, L-длина окружности, D- диаметр окружности, “пи”=3,14
Длину окружности, найдем из следующей информации: “….металлические дуги в форме полуокружности длиной 5,53 метра….”
Поскольку известна длина полуокружности – 5,53 м, то длина окружности равна:
Из этих расчетов получаем, что ширина теплицы (с округлением до сотых) равна 3,52
4) Найти ширину центральной грядки, если она в два раза больше ширины узкой грядки. Ответ дайте до десятков, с точностью до десятков.
Для ответе на этот вопрос, сделаем схематический чертеж:
В этой задаче, за Х взяли ширину узкой грядки. Тогда широкая грядка будет 2Х. В задаче у нас две дорожки, что показано на схеме, которые составляю по 50 см.
По схеме составим уравнение:
Поскольку в задаче написано условие, что результат нужно округлить до десятков, поэтому получаем ответ 130.
5)Найти высоту входа в теплицу. Ответ дайте в сантиметрах.
Для расчета высоты теплицы, нам необходимо сделать дополнительные построения. Проводим ОС1. Получаем прямоугольный треугольник, ОС1С. Дальше по теореме Пифагора, выразим СС1. Для этой задачи, покажу три разных варианта завершения задачи.
Первый вариант:
При таком решении, получаем неизвлекаемый корень из 3. На экзамене, хорошо, что хоть кто нибудь вспомнит, что примерно он равен 1,7. Но такого значения не достаточно, поскольку мы получаем, что высота входа равна 149,6. Но такой ответ нас не устраивает, поскольку верный ответ находится в интервале от 150-160 см
Поэтому в этой задаче, чем точнее ответ, тем больше вероятность, что ответ будет не верный, не попадете в интервал правильного ответа.
Второй вариант:
В этом варианте, мы не будем раскладывать числа до последнего множителя, а будем раскладывать число на множители таким образом, что бы получилось приближенное число из таблицы квадратов. В этом случае, 23232 можно поделить на 16 (признак делимости на 4, если последние два числа делятся на 4)
Как видите, оба ответа, 152 и 156 подходят под наш интервал решения.
Третий вариант: воспользуемся канадской формулой вычисления приближенного значения квадратного корян.
Как видим, эту формулу. так же можно использовать для решения этой задачи.
Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.
Задача решается последовательно.
Что нам нужно?
Узнать сначала ширину входа.
Она равна половине от ширины самой теплицы.
Как понятно из чертежа, ширина таплицы – это диаметр окружности. В окружности нам известна длина ее половины. По условию задачи – это 5,2 (условно метра)
Значит длина полной окружности будет 10,4.
Зная длину окружности по формуле вычислим ее диаметр.

10,4 : 3,14 = 3,31, округляем = 3,3
Теперь рассмотрим прямоугольный треугольник ОDВ.
Почему он прямоугольный?
Да потому что при постройке таких дверей вертикаль по отношению к земле всегда находится под углом 90 градусов. Перекосы недопустимы.
Гипотенуза треугольника нам известна – это по сути радиус окружности, то есть – половина от диаметра, мы его только что вычислили.
Один из катетов ОВ тоже известен – это 14 диаметра окружности (по условию).
Остается применить теорему Пифагора и вычислить другой катет прямоугольного треугольника – DВ. Который и представляет собой высоту входа.

ОВ = 3,3 : 4 = 0,825
OD = 3,3 : 2 = 1,65
Применим формулу

Произведем вычисления (которые я опускаю)
Результат будет 1.4 (условных метров).
Низковато для человека среднего роста, придется при входе наклонять голову.
В 2022 учебном году выпускники 9 классов будут сдавать ОГЭ по обновлённым заданиям. Представляем вам вариант тренировочной работы по математике в формате ОГЭ от СтатГрада. Обычно статградовские задания, используемые на пробных тестированиях в школах, максимально приближены к реальным экзаменационным вариантам. Рассказываем, как работать с новыми заданиями про теплицу.
Хотите БЕСПЛАТНО разобрать с опытным преподавателем все детали новых усложнённых вариантов ОГЭ по математике 2023 года – приходите на пробное занятие в Lancman School. Решите продолжить готовиться к ОГЭ вместе с нами весь год – дадим скидку после бесплатного пробного занятия.
Любой вопрос смело пишите сюда. Мы 13 лет готовим к ОГЭ на высокие баллы. Прокачиваем знания даже самых слабых учеников. Гаранитруем получение оценки “5” на ОГЭ. Офисы Курсов ОГЭ Lancman School есть на каждой ветке московского метро.
Если хотите сэкономить, но получить при этом качественную подготовку, записывайтесь на наши онлайн-курсы ОГЭ-2023 по русскому языку, математике, обществознанию и английскому языку.
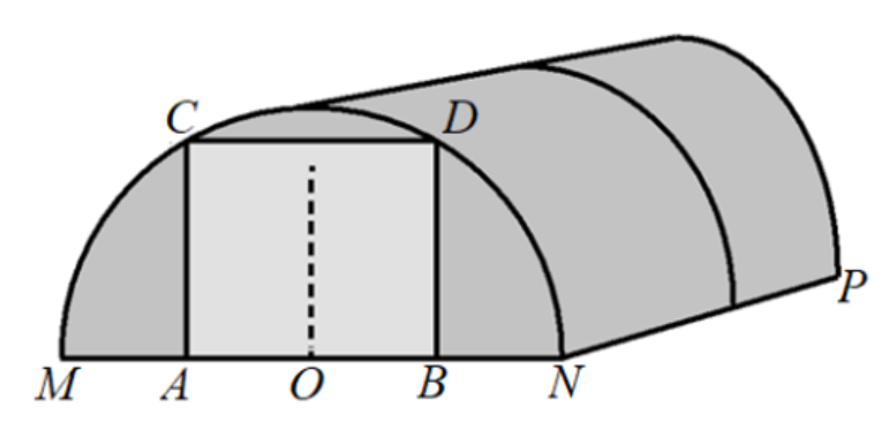
Алексей Юрьевич решил построить на дачном участке теплицу длиной NP = 4,5 м. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Алексей Юрьевич заказывает металлические дуги в форме полуокружностей длиной 5,2 м каждая и плёнку для обтяжки. В передней стенке планируется вход, показанный на рисунке прямоугольником ACDB. Точки A и B — середины отрезков MO и ON соответственно.
1. Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 60 см?
Решение:
Решать подобные задания лучше наглядным способом, то есть нарисовать предварительно дугу и делать на ней необходимые пометки.
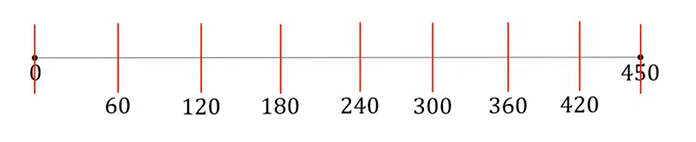
Ответ: 9.
2. Найдите примерную ширину MN теплицы в метрах. Число π возьмите равным 3,14. Результат округлите до десятых.
Решение:
Длину МN необходимо искать, исходя из дуги, используя формулу длины окружности. Поскольку MN – это полуокружность, то ее длина равна πR.
πR=5,2
3,14R=5,2
R=5,2/3,14
MN=2 × 520/314=520/157
MN=3,31
Ответ: 3,3
3. Найдите примерную площадь участка внутри теплицы в квадратных метрах. Ответ округлите до целых.
Решение:
Площадь участка внутри теплицы представляет собой прямоугольник, и его площадь равна MN × NP.
S=520/157 × 4,5= 2340/157=14,9… При округлению получаем 15.
Можно взять ответ в 3,3 из предыдущего задания для решения.
S=3,3 × 4,5=14,85. При округлении тоже получаем 15.
Ответ: 15.
4. Сколько квадратных метров плёнки нужно купить для теплицы с учётом передней и задней стенок, включая дверь? Для крепежа плёнку нужно покупать с запасом 10 %. Число π возьмите равным 3,14. Ответ округлите до целых.
Решение:
Для начала необходимо посчитать площадь крыши теплицы. Она представляет собой прямоугольник со сторонами, равными 4,5 и 5,2.
S крыши=5,2 × 4,5=23,4
Остаётся посчитать площадь двух полуокружностей (перед и задняя часть теплицы). Вместе это одна окружность – значит, можно не считать площадь 2 раза.
S стенок=3,14 × (260/157)в квадрате=314/100 × 260/157 × 260/157=1352/157
К данной площади необходимо добавить 10%, поскольку плёнки надо купить с запасом. Прибавляем по 10% к уже имеющимся цифрам.
S крыши=25,74
S стенок=9,47…
Складываем и округляем. Получаем примерно 35 метров плёнки.
Ответ: 35.
5. Найдите примерную высоту входа в теплицу в метрах. Число π возьмите равным 3,14. Ответ округлите до десятых.
Решение:
Задача геометрическая: нам надо представить, что перед нами равносторонний треугольник.
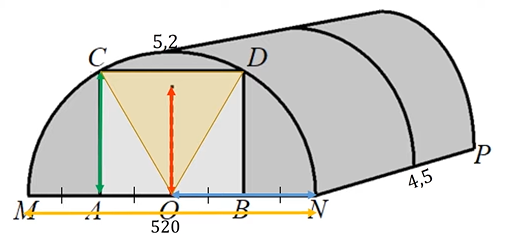
Итак, перед нами равносторонний треугольник СOD. Найдя его высоту, мы найдём высоту входа в теплицу. Будем использовать формулу высоты равностороннего треугольника. Сторона треугольника COD равна радиусу окружности, которую мы уже знаем (260/157).
h=1,40… Округляем до 1,4.
Ответ: 1,4.
Ваш ребёнок – школьник 1-11 класса? Вы учитель? Отлично! Мы пишем для вас. Узнавайте от нас первыми новости образования, актуальную информацию об экзаменах и просто полезные советы. Кнопка подписки прямо под постом!
Фото: pixabay.com
Прочитайте внимательно текст и выполните залдания 1 — 5.
Сергей Петрович решил построить на дачном участке теплицу длиной 4 м. Для этого он сделал прямоугольный фундамент.
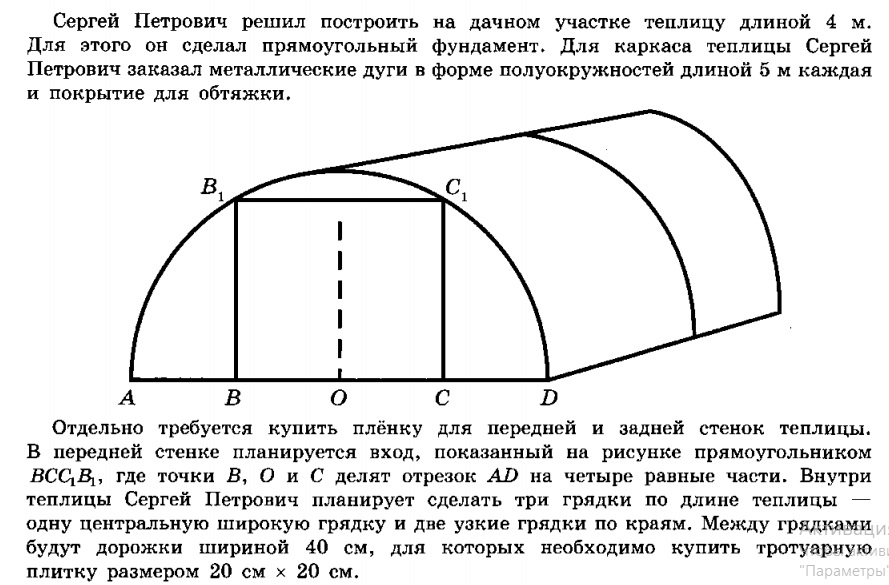
Задание 1 (ОГЭ 2020)
Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 60 см?
Решение: Длина теплицы составляет 4 м = 400 см. Рассчитаем количество дуг для теплицы, соблюдая условие: расстояние между соседними дугами меньше или равно 60 см. Разделим 400 на 60. Получится 6 дуг и в остатке 40 см. Учитывая две крайние дуги, получается:6 + 2 = 8 (дуг).
Ответ: 8.
Задание 2 (ОГЭ 2020)
Сколько упаковок плитки необходимо купить для дорожек между грядками, если она продается в упаковках по 6 штук?
Решение: Из условия задачи имеем, что грядок в теплице планируется 3. Дорожек будет 2. Длина дорожки совпадает с длиной теплицы, то есть 4 м = 400 см. Ширина дорожки — 40 см. Найдем площадь двух дорожек. 2 * 40 * 400 = 32000 (кв. см).
Площадь одной плитки: 20 * 20 = 400 (кв. см).
32000 : 400 = 80 (штук) плиток нужно купить для двух дорожек.
80 : 6 = 13 (остаток 2).
Понадобится 13 + 1 = 14 упаковок плитки.
Ответ: 14.
Задание 3 (ОГЭ 2020)
Найдите ширину теплицы. Ответ дайте в метрах с точностью до десятых.
Решение:
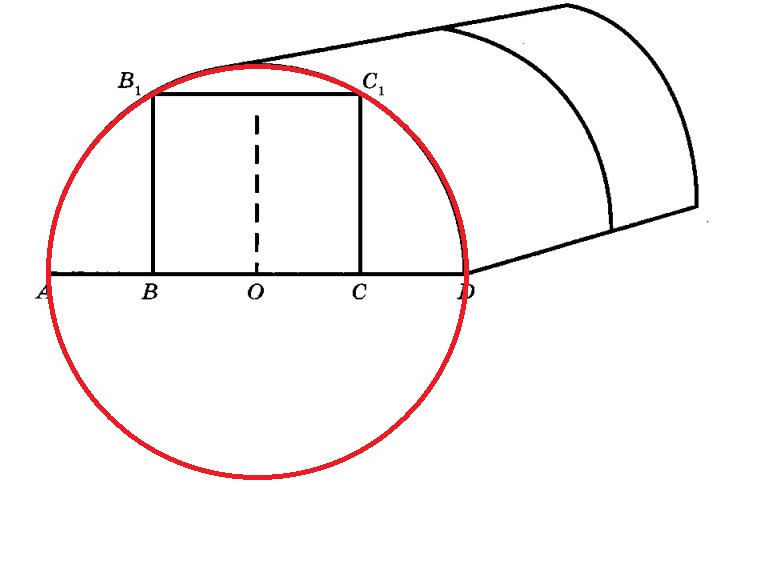
Дуги для теплицы имеют форму полуокружности. Чтобы найти ширину теплицы, нужно достроить окружность и найти радиус окружности OD.
Ширина теплицы AD является диаметром окружности. AD = 2 * OD.
Длина дуги теплицы равна 5 м и вычисляется по формуле П * OD (это длина полуокружности).
OD = 5 : 3,14 = 1,6 (м).
AD = 2 * OD = 2 * 1,6 = 3,2 (м).
Ответ: 3,2.
Задание 4 (ОГЭ 2020)
Найдите ширину центральной грядки, если она в два раза больше ширины узкой грядки. Ответ дайте в сантиметрах с точностью до десятых.
Решение: Ширина теплицы 3,2 м = 320 см. В теплице есть 2 дорожки по 40 см и три грядки. Пусть ширина узкой грядки х см, тогда широкой грядки — 2х см.
Составим уравнение 2х + х + х + 2 * 40 = 320 и решим его.
4х + 80 = 320,
4х = 320 — 80,
4х = 240,
х = 60 (см) — ширина узкой грядки.
Найдем ширину центральной грядки (широкой). 2х = 2 * 60 = 120 (см).
Ответ: 120.
Задание 5 (ОГЭ 2020)
Найдите высоту входа в теплицу. Ответ дайте в сантиметрах.
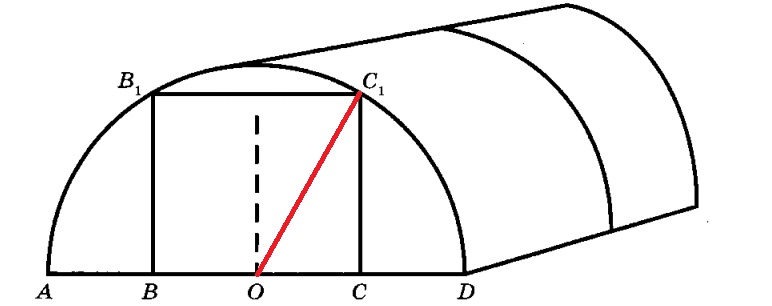
Чтобы найти высоту входа в теплицу,нужно рассмотреть прямоуголный треугольник OC1A. Применив теорему Пифагора, вычислим высоту CC1 теплицы.
По условию AB = BO = OC = CD = 320 см : 4 = 80 см.
ОС1 = OD = 160 см — радиусы.
По теореме Пифагора имеем: СС1 = 80√3 см = 136 см.
Ответ: 136.
Подробный ОГЭ 2020 — земледелец устраивает на склонах гор терассы — задания 1 — 5.
Версия для печати и копирования в MS Word
Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 60 см?
Алексей Юрьевич решил построить на дачном участке теплицу длиной NP = 4,5 м. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Алексей Юрьевич заказывает металлические дуги в форме полуокружностей длиной 5,2 м каждая и плёнку для обтяжки. В передней стенке планируется вход, показанный на рисунке прямоугольником ACDB. Точки A и B — середины отрезков MO и ON соответственно.
Спрятать решение
Решение.
Переведем 60 см = 0,6 м. Найдем количество промежутков между дугами: 4,5 : 0,6 = 7,5, следовательно, наименьшее количество промежутков — 8. Количество дуг на единицу больше, чем количество промежутков: 8 + 1 = 9.
Ответ: 9.
1
Найдите примерную ширину MN теплицы в метрах. Число π возьмите равным 3,14. Результат округлите до десятых.
2
Найдите примерную площадь участка внутри теплицы в квадратных метрах. Ответ округлите до целых.
3
Сколько квадратных метров плёнки нужно купить для теплицы с учётом передней и задней стенок, включая дверь? Для крепежа плёнку нужно покупать с запасом 10 %. Число π возьмите равным 3,14. Ответ округлите до целых.
4
Найдите примерную высоту входа в теплицу в метрах. Число π возьмите равным 3,14. Ответ округлите до десятых.
