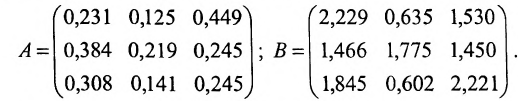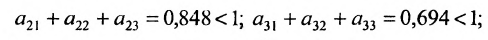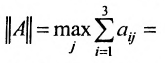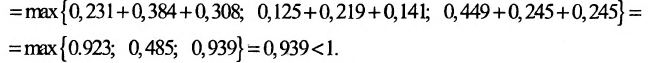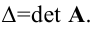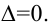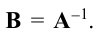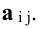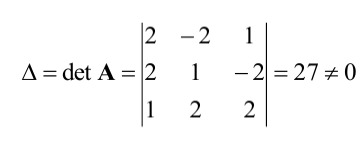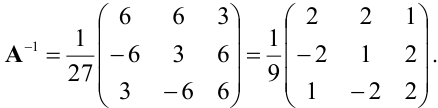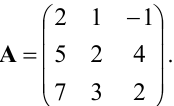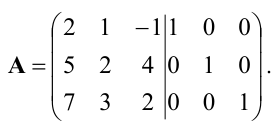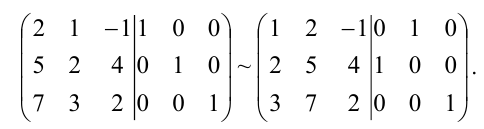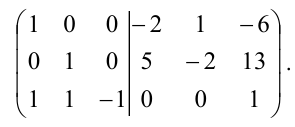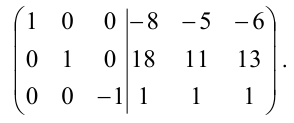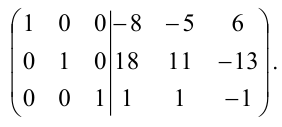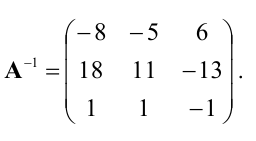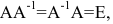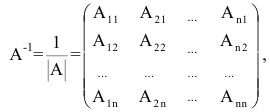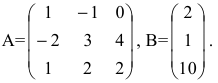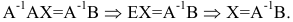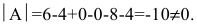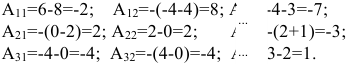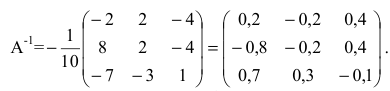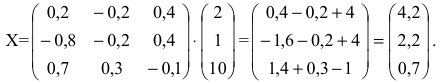Как найти обратную матрицу
- Быстрый способ для матриц $2 times 2$
- Пример 1
- Пример 2
- Нахождение с помощью метода Гаусса
- Пример 3
- Пример 4
- Метод союзной матрицы(алгебраические дополнения)
- Пример 5
Обратная матрица обозначается $ A^{-1} $ и существует только для матриц, у которых определитель не равен нулю $ det A neq 0 $.
Быстрый способ для матриц $2 times 2$
Пусть задана матрица $A = begin{pmatrix} a&b\c&d end{pmatrix}$. Для быстрого способа нахождения обратной матрицы необходимо поменять местами элементы стоящие на главной диагонали, а для оставшихся элементов поменять знак на противоположный. Затем каждый элемент разделить матрицы разделить на определитель исходной матрицы. Математическая формула выглядит следующим образом $$A^{-1} = frac{1}{det A} begin{pmatrix} d&-b \ -c&a end{pmatrix} = frac{1}{ad-bc} begin{pmatrix} d&-b \ -c&a end{pmatrix}.$$
| Пример 1 |
| Найти обратную матрицу для $A = begin{pmatrix} 3&4 \ 5&9 end{pmatrix}$. |
| Решение |
|
Первым делом вычисляем определитель и убеждаемся, что он не равен нулю $$det A = begin{vmatrix} 3&4 \ 5&9 end{vmatrix} = 3cdot9 – 4cdot5 = 27 – 20 = 7.$$ Итак, определитель не равен нулю, значит, обратная матрица существует. Продолжаем наш алгоритм. Меняем элементы на главной диагонали местами, а у оставшихся элементов меняем знак на противоположный. $$A^{-1} = frac{1}{7} begin{pmatrix} 9&-4 \ -5&3 end{pmatrix} = begin{pmatrix} frac{9}{7}&frac{-4}{7} \ frac{-5}{7}&frac{3}{7} end{pmatrix}.$$ |
| Ответ |
| $$A^{-1} = begin{pmatrix} frac{9}{7}&frac{-4}{7} \ frac{-5}{7}&frac{3}{7} end{pmatrix}$$ |
| Пример 2 |
| Вычислить обратную матрицу для $A = begin{pmatrix} 2&-1 \ 4&-6 end{pmatrix}$. |
| Решение |
|
Находим определитель $$det A = begin{vmatrix} 2&-1 \ 4&-6 end{vmatrix} = 2cdot(-6) – 4cdot(-1) = -12 + 4 = -8.$$ Меняем местами элементы главной диагонали, а остальным меняем знак на противоположный. Не забываем затем каждый элемент разделить на определитель. $$A^{-1} = frac{1}{-8} begin{pmatrix} -6&1 \ -4&2 end{pmatrix} = begin{pmatrix} frac{-6}{-8}&frac{1}{-8} \ frac{-4}{-8}&frac{2}{-8} end{pmatrix} = begin{pmatrix} frac{3}{4}&-frac{1}{8} \ frac{1}{2}&-frac{1}{4} end{pmatrix}$$ |
| Ответ |
| $$A^{-1} = begin{pmatrix} frac{3}{4}&-frac{1}{8} \ frac{1}{2}&-frac{1}{4} end{pmatrix}$$ |
Нахождение с помощью метода Гаусса
На практике чаще всего метод Гаусса используется как способ нахождения обратной матрицы. Суть метода в том, что к основной матрице добавляется дополнительная единичная матрица с такой же размерностью.
$$ Bigg (begin{matrix} a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33} end{matrix} Bigg | begin{matrix} 1&0&0\0&1&0\0&0&1 end{matrix} Bigg ) $$
Далее нужно путем простейших элементарных преобразований привести левую матрицу к единичной, а одновременно с ней справа получится обратная матрица:
$$ Bigg (begin{matrix} 1&0&0\0&1&0\0&0&1 end{matrix} Bigg | begin{matrix} b_{11}&b_{12}&b_{13}\b_{21}&b_{22}&b_{23}\b_{31}&b_{32}&b_{33} end{matrix} Bigg ) $$
$$A^{-1} = begin{pmatrix} b_{11}&b_{12}&b_{13}\b_{21}&b_{22}&b_{23}\b_{31}&b_{32}&b_{33} end{pmatrix}$$
| Пример 3 |
| Найти обратную матрицу элементарными преобразованиями $$A = begin{pmatrix} 2&-1&0 \ 0&2&-1 \ -1&-1&1 end{pmatrix}.$$ |
| Решение |
|
Вычисляем определитель матрицы, чтобы убедиться что он не равен нулю $$det A = begin{vmatrix} 2&-1&0 \ 0&2&-1 \ -1&-1&1 end{vmatrix} = 4-1+0-0-2-0=1 neq 0.$$ Выписываем основную матрицу и добавляем справа единичную матрицу. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&-1 &|& 0&1&0 \ -1&-1&1 &|& 0&0&1 end{pmatrix}$$ Проводим элементарные преобразования над строками матриц таким образом, чтобы слева получилась единичная матрица. В то же время как справа получим обратную матрицу. Умножаем третью строку на 2 и прибавляем первую. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&-1 &|& 0&1&0 \ 0&-3&2 &|& 1&0&2 end{pmatrix}$$ Умножаем третью строку на 2 и прибавляем к ней вторую строку, умноженную на 3. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&-1 &|& 0&1&0 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$ Теперь запускаем обратный ход преобразований снизу вверх. Ко второй строке прибавляем третью. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&0 &|& 2&4&4 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$ Умножаем первую строку на 2 и прибавляем к ней вторую строчку матрицы. $$begin{pmatrix} 4&0&0 &|& 4&4&4 \ 0&2&0 &|& 2&4&4 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$ Теперь, чтобы слева получилась единичная матрица нужно первую строку разделить на 4, вторую на 2. $$begin{pmatrix} 1&0&0 &|& 1&1&1 \ 0&1&0 &|& 1&2&2 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$ Справа как видим получилась обратная матрица $$A^{-1} = begin{pmatrix} 1&1&1 \ 1&2&2 \ 2&3&4 end{pmatrix}.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$A^{-1} = begin{pmatrix} 1&1&1 \ 1&2&2 \ 2&3&4 end{pmatrix}$$ |
| Пример 4 |
| Дана матрица, найти обратную $$A = begin{pmatrix} 3&2&1 \ 1&0&2 \ 4&1&3 end{pmatrix}.$$ |
| Решение |
|
Первым делом вычисляем определитель, чтобы убедиться в существовании обратной матрицы $$det A = begin{vmatrix} 3&2&1 \ 1&0&2 \ 4&1&3 end{vmatrix} = 0+16+1-0-6-6=5.$$ Теперь справа от матрицы дописываем единичную матрицу $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 1&0&2 &|& 0&1&0 \ 4&1&3 &|& 0&0&1 end{pmatrix}.$$ Теперь с помощью элементарных преобразований делаем так, чтобы слева стояла единичная матрица. А справа получим одновременно обратную матрицу. Умножаем вторую строку на 3 и вычитаем из неё первую. Умножаем третью строчку на 3 и вычитаем первую, умноженную на 4. $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 0&-2&5 &|& -1&3&0 \ 0&-5&5 &|& -4&0&3 end{pmatrix}$$ Умножаем третью строку на 2 и вычитаем вторую, умноженную на 5. $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 0&-2&5 &|& -1&3&0 \ 0&0&-15 &|& -3&-15&6 end{pmatrix}$$ Третью строку можно разделить на 3, чтобы уменьшить числа для дальнейшего удобства. Сделаем это. $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 0&-2&5 &|& -1&3&0 \ 0&0&-5 &|& -1&-5&2 end{pmatrix}$$ Начинаем проводить преобразования над строками теперь снизу вверх. Умножаем первую строку на 5 и прибавляем к ней третью. Ко второй строке просто прибавляем третью. $$begin{pmatrix} 15&10&0 &|& 4&-5&2 \ 0&-2&0 &|& -2&-2&2 \ 0&0&-5 &|& -1&-5&2 end{pmatrix}$$ К первой строке прибавляем вторую, умноженную на 5. $$begin{pmatrix} 15&0&0 &|& -6&-15&12 \ 0&-2&0 &|& -2&-2&2 \ 0&0&-5 &|& -1&-5&2 end{pmatrix}$$ Осталось разделить первую строку на 15, вторую на (-2), а третью на (-5). $$begin{pmatrix} 1&0&0 &|& -frac{2}{5}&-1&frac{4}{5} \ 0&1&0 &|& 1&1&-1 \ 0&0&1 &|& frac{1}{5}&1&-frac{2}{5} end{pmatrix}$$ |
| Ответ |
| $$begin{pmatrix} 1&0&0 &|& -frac{2}{5}&-1&frac{4}{5} \ 0&1&0 &|& 1&1&-1 \ 0&0&1 &|& frac{1}{5}&1&-frac{2}{5} end{pmatrix}$$ |
Метод союзной матрицы(алгебраические дополнения)
Формула нахождения обратной матрицы через алгебраические дополнения выглядит следующим образом
$$A^{-1} = frac{1}{|A|} (A^*)^T. $$
Матрица $A^*$ называется союзной (присоединенной) матрицей и представляет собой набор алгебраических дополнений матрицы $ A $:
$$ A^* = begin{pmatrix} A_{11}&A_{12}&A_{13}\A_{21}&A_{22}&A_{23}\A_{31}&A_{22}&A_{33} end{pmatrix}, text{ где } A_{ij}=(-1)^{i+j} M_{ij} $$
$M_{ij} $ называется минором матрицы, который получается путем вычеркивания $ i $-ой строки и $ j $-того столбца из матрицы.
| Пример 5 |
| Найти обратную матрицу методом алгебраических дополнений $$ A = begin{pmatrix} 3&1&2\-1&3&-2\0&-1&4 end{pmatrix} $$ |
| Решение |
|
Итак, пользуемся формулой $ A^{-1} = frac{1}{|A|} (A^*)^T $ Первым делом вычисляем определитель матрицы $ A $, так как необходимым условием существование обратной матрицы является неравенство его к нулю: $$ |A| = begin{vmatrix} 3&1&2\-1&3&-2\0&-1&4 end{vmatrix} = 36 + 0 + 2 – 0 – 6 + 4 = 36 neq 0 $$ Находим алгебраические дополнения матрицы $ A $. Для этого удаляем все элементы стоящие в i-ой строке и в j-ом столбце. Оставшиеся элементы матрицы переписываем в определитель и проводим его вычисление. Вычеркиваем первую строку и первый столбец: $$ A_{11} = (-1)^{1+1} cdot begin{vmatrix} 3&-2\-1&4 end{vmatrix} = 12 – 2 = 10 $$ Убираем первую строку и второй столбец: $$ A_{12} = (-1)^{1+2} cdot begin{vmatrix} -1&-2\0&4 end{vmatrix} = -(-4 – 0) = 4 $$ Оставшиеся алгебраические дополнения находим по аналогии с предыдущими двумя. $$ A_{13} = (-1)^{1+3} cdot begin{vmatrix} -1&3\0&-1 end{vmatrix} = 1 – 0 = 1 $$ $$ A_{21} = (-1)^{2+1} cdot begin{vmatrix} 1&2\-1&4 end{vmatrix} = -(4 + 2) = -6 $$ $$ A_{22} = (-1)^{2+2} cdot begin{vmatrix} 3&2\0&4 end{vmatrix} = 12 – 0 = 12 $$ $$ A_{23} = (-1)^{2+3} cdot begin{vmatrix} 3&1\0&-1 end{vmatrix} = -(-3 – 0) = 3 $$ $$ A_{31} = (-1)^{3+1} cdot begin{vmatrix} 1&2\3&-2 end{vmatrix} = -2 – 6 = -8 $$ $$ A_{32} = (-1)^{3+2} cdot begin{vmatrix} 3&2\-1&-2 end{vmatrix} = -(-6 + 2) = 4 $$ $$ A_{33} = (-1)^{3+3} cdot begin{vmatrix} 3&1\-1&3 end{vmatrix} = 9+1 = 10 $$ Составляем союзную (присоединенную) матрицу $ A^* $ из алгебраических дополнений: $$ A^* = begin{pmatrix} 10&4&1\-6&12&3\-8&4&10 end{pmatrix}. $$ Транспонируем её и обозначаем $ (A^*)^T $: $$ (A^*)^T = begin{pmatrix} 10&-6&-8\4&12&4\1&3&10 end{pmatrix} $$ В итоге находим обратную матрицу $ A^{-1} $: $$ A^{-1} = frac{1}{36} begin{pmatrix} 10&-6&-8\4&12&4\1&3&10 end{pmatrix} $$ Делим каждый элемент матрицы на 36 и получаем следующее: $$begin{pmatrix} frac{5}{18}&-frac{1}{6}&-frac{2}{9}\ frac{1}{9}&frac{1}{3}&frac{1}{9}\frac{1}{36}&frac{1}{12}&frac{5}{18} end{pmatrix}.$$ |
| Ответ |
| $$A^{-1} =begin{pmatrix} frac{5}{18}&-frac{1}{6}&-frac{2}{9}\ frac{1}{9}&frac{1}{3}&frac{1}{9}\frac{1}{36}&frac{1}{12}&frac{5}{18} end{pmatrix}$$ |
Матрица BB является обратной матрицей к квадратной матрице AA, если AB=BA=EAB = BA = E.
Из определения можно понять, что обратная матрица BB будет квадратной матрицей аналогичного порядка, какой имеет матрица AA (иначе какое-либо из произведений ABAB или BABA будет не определено).
Обратная матрица для исходной матрицы AA определяется так: A−1A^{-1}. Можно утверждать, что если A−1A^{-1} существует, то AA−1=A−1A=EAA^{-1} = A^{-1} A= E.
Также легко видеть, что (A−1)−1=A(A^{-1})^{-1} = A.
Если детерминант матрицы является нулем, то обратную к ней матрицу нельзя получить.
Онлайн-калькулятор
Квадратную матрицу AA можно назвать вырожденной матрицей тогда, когда определитель матрицы AA равен нулю, и невырожденной, если определитель не равен нулю.
В том случае, если обратная матрица может существовать, то она будет единственной.
Формула для вычисления обратной матрицы
Обратную матрицу A−1A^{-1} к матрице AA можно найти по формуле:
A−1=1detA⋅A∗A^{-1}=frac{1}{det A}cdot A^*
detAdet A — определитель матрицы A,A,
A∗A^* — транспонированая матрица алгебраических дополнений к матрице A.A.
Нужно найти обратную матрицу для следующей матрицы:
A=(1−20 342 −131)A = begin{pmatrix}
1& -2 & 0\
3 & 4 & 2\
-1& 3& 1 \
end{pmatrix}
Решение
Вычислим детерминант:
detA=∣1−20342−131∣=1∣4231∣−(−2)∣32−11∣+0∣34−13∣=8det A = begin{vmatrix}
1 & -2 & 0 \
3 & 4 & 2 \
-1 & 3 & 1 \
end{vmatrix} = 1 begin{vmatrix}
4 & 2 \
3 & 1 \
end{vmatrix} – (-2) begin{vmatrix}
3 & 2 \
-1 & 1 \
end{vmatrix} +0 begin{vmatrix}
3 & 4 \
-1 & 3 \
end{vmatrix} = 8
Так как detA≠0det A neq 0, то матрица – невырожденная, и обратная для нее существует.
Посчитаем алгебраические дополнение:
A11=(−1)1+1∣4231∣=−2,A_{11} = (-1)^{1+1} begin{vmatrix}
4 & 2 \
3 & 1 \
end{vmatrix} = -2,
A12=(−1)1+2∣32−11∣=−5,A_{12} = (-1)^{1+2} begin{vmatrix}
3 & 2 \
-1 & 1 \
end{vmatrix} = -5,
A13=(−1)1+3∣34−13∣=13A_{13} = (-1)^{1+3} begin{vmatrix}
3 & 4 \
-1 & 3 \
end{vmatrix} = 13,
A21=(−1)2+1∣−2031∣=2A_{21} = (-1)^{2+1} begin{vmatrix}
-2 & 0 \
3 & 1 \
end{vmatrix} = 2,
A22=(−1)2+2∣10−11∣=1A_{22} = (-1)^{2+2} begin{vmatrix}
1 & 0 \
-1 & 1 \
end{vmatrix} = 1,
A23=(−1)2+3∣1−2−13∣=−1A_{23} = (-1)^{2+3} begin{vmatrix}
1 & -2 \
-1 & 3 \
end{vmatrix} = -1,
A31=(−1)3+1∣−2042∣=−4A_{31} = (-1)^{3+1} begin{vmatrix}
-2 & 0 \
4 & 2 \
end{vmatrix} = -4,
A32=(−1)3+2∣1032∣=−2A_{32} = (-1)^{3+2} begin{vmatrix}
1 & 0 \
3 & 2 \
end{vmatrix} = -2,
A33=(−1)3+3∣1−234∣=10.A_{33} = (-1)^{3+3} begin{vmatrix}
1 & -2 \
3 & 4 \
end{vmatrix} = 10.
Обратная матрица:
A−1=18(−22−4−51−213−110)A^{-1} = frac{1}{8} begin{pmatrix}
-2 & 2 & -4 \
-5 & 1 & -2 \
13 & -1 & 10 \
end{pmatrix}
Чтобы избежать ошибок, необходимо сделать проверку: для этого нужно посчитать произведение первоначальной матрицы на конечную. Если в результате получится единичная матрица, то вы нашли обратную матрицу безошибочно.
Найдите обратную матрицу для матрицы:
A=(13−25)A = begin{pmatrix}
1 & 3\
-2 & 5 \
end{pmatrix}
Решение
detA=11≠0→A−1det A= 11 neq 0 rightarrow A^{-1} – существует.
A11=(−1)1+1⋅5=5A_{11} = (-1)^ {1+1} cdot 5 = 5,
A12=(−1)1+2⋅(−2)=2A_{12} = (-1)^ {1+2} cdot (-2) = 2,
A21=(−1)2+1⋅3=−3A_{21} = (-1)^ {2+1} cdot 3 = -3,
A22=(−1)2+2⋅1=1.A_{22} = (-1)^ {2+2} cdot 1 = 1.
Ответ:
A−1=111(5−321)A^{-1} = frac{1}{11} begin{pmatrix}
5 & -3 \
2 & 1 \
end{pmatrix}
Нами был рассмотрен способ нахождения матрицы с помощью алгебраических дополнений. Существует еще один способ, который называется методом элементарных преобразований.
Метод элементарных преобразований
Метод основан на элементарных преобразованиях матриц, под которыми будем понимать такие преобразования, в результате которых сохраняется эквивалентность матриц:
- перестановка местами любых двух рядов (строк или столбцов) матрицы;
- умножение любого ряда матрицы (строки или столбца) на некоторое число, отличное от нуля;
- прибавление к любому ряду (строке или столбцу) матрицы другого ряда (строки или столбца), умноженного на некоторое число, отличное от нуля.
Рассмотрим алгоритм нахождения обратной матрицы данным методом.
Алгоритм нахождения обратной матрицы методом элементарных преобразований
- Из исходной матрицы AA и единичной матрицы EE того же порядка составить расширенную матрицу, т.е. матрицу вида (A∣E)begin{pmatrix}A|Eend{pmatrix}.
- С помощью элементарных преобразований над строками расширенной матрицы получить единичную матрицу слева от черты: (E∣A−1)begin{pmatrix}E|A^{-1}end{pmatrix}.
- Выписать обратную матрицу, которая находится справа от черты.
Найти матрицу K−1K^{-1}, если K=(1301)K=begin{pmatrix}1&3\0&1end{pmatrix}.
Из матрицы KK второго порядка и единичной матрицы второго порядка составим расширенную матрицу:
(1301∣1001)begin{pmatrix}left.begin{matrix}1&3\0&1end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}.
Произведем элементарные преобразования расширенной матрицы.
Прибавим к строке №1 строку №3, умноженную на -3:
(1301∣1001)∼(1001∣1−301)begin{pmatrix}left.begin{matrix}1&3\0&1end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0\0&1end{matrix}right|begin{matrix}1&-3\0&1end{matrix}end{pmatrix}.
Слева получили единичную матрицу.
Выпишем обратную матрицу:
K−1=(1−301)K^{-1}=begin{pmatrix}1&-3\0&1end{pmatrix}.
Сделаем проверку, чтобы убедиться в том, что найденная матрица действительно является обратной.
K⋅K−1=(1301)⋅(1−301)=(1⋅1+3⋅01⋅(−3)+3⋅10⋅1+1⋅00⋅(−3)+1⋅1)=(1001)Kcdot K^{-1}=begin{pmatrix}1&3\0&1end{pmatrix}cdotbegin{pmatrix}1&-3\0&1end{pmatrix}=begin{pmatrix}1cdot1+3cdot0&1cdot(-3)+3cdot1\0cdot1+1cdot0&0cdot(-3)+1cdot1end{pmatrix}=begin{pmatrix}1&0\0&1end{pmatrix}.
Значит, обратная матрица найдена правильно.
Найти матрицу F−1F^{-1}, если F=(110010033)F=begin{pmatrix}1&1&0\0&1&0\0&3&3end{pmatrix}.
Из матрицы FF третьего порядка и единичной матрицы третьего порядка составим расширенную матрицу:
(110010033∣100010001)begin{pmatrix}left.begin{matrix}1&1&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&0&0\0&1&0\0&0&1end{matrix}end{pmatrix}.
Произведем элементарные преобразования расширенной матрицы.
Прибавим к строке №1 строку №2, умноженную на -1:
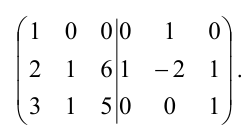
(110010033∣100010001)∼(100010033∣1−10010001)begin{pmatrix}left.begin{matrix}1&1&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&0&0\0&1&0\0&0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&0&1end{matrix}end{pmatrix}.
Прибавим к строке №3 строку №2, умноженную на -3:
(100010033∣1−10010001)∼(100010003∣1−100100−31)begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&0&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&-3&1end{matrix}end{pmatrix}.
Умножим строку №3 на 13frac{1}{3}:
(100010003∣1−100100−31)∼(100010001∣1−100100−113)begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&0&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&-3&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&0&1end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&-1&frac{1}{3}end{matrix}end{pmatrix}.
Слева получили единичную матрицу.
Выпишем обратную матрицу:
F−1=(1−100100−113)F^{-1}=begin{pmatrix}1&-1&0\0&1&0\0&-1&frac{1}{3}end{pmatrix}.
Сделаем проверку, чтобы убедиться в том, что найденная матрица действительно является обратной.
F⋅F−1=(110010033)⋅(1−100100−113)=(100010001)Fcdot F^{-1}=begin{pmatrix}1&1&0\0&1&0\0&3&3end{pmatrix}cdotbegin{pmatrix}1&-1&0\0&1&0\0&-1&frac{1}{3}end{pmatrix}=begin{pmatrix}1&0&0\0&1&0\0&0&1end{pmatrix}.
Значит, обратная матрица найдена правильно.
Выполнение контрольных работ на заказ недорого от профильных авторов на бирже Студворк!
Обра́тная ма́трица — такая матрица 


Обратную матрицу можно определить как:
- где
— соответствующая присоединённая матрица,
— определитель матрицы
.
Из этого определения следует критерий обратимости: матрица обратима тогда и только тогда, когда она невырождена, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.
Свойства обратной матрицы[править | править код]
Пусть квадратные матрицы 
Способы нахождения обратной матрицы[править | править код]
Если матрица обратима, то для нахождения обратной матрицы можно воспользоваться одним из следующих способов:
Точные (прямые) методы[править | править код]
Метод Жордана—Гаусса[править | править код]
Возьмём две матрицы: саму 



При использовании метода Гаусса первая матрица будет умножаться слева на одну из элементарных матриц 
Вторая матрица после применения всех операций станет равна 

С помощью матрицы алгебраических дополнений[править | править код]
Матрица, обратная матрице 
- где
— присоединенная матрица (матрица, составленная из алгебраических дополнений для соответствующих элементов транспонированной матрицы).
Сложность алгоритма зависит от сложности 

Использование LU- или LUP-разложения[править | править код]
Матричное уравнение 

















Матрицу, обратную к заданной невырожденной матрице 
Результатом LUP-разложения матрицы 

















В случае использования LU-разложения (


Сложность обоих алгоритмов — 
Итерационные методы[править | править код]
Матрицу 
Последовательность матриц 


Выбор начального приближения[править | править код]
Проблема выбора начального приближения 

















Для метода Ньютона в качестве начального приближения можно выбрать 






Примеры[править | править код]
Матрица 2 × 2[править | править код]
[4]
Обращение матрицы 2 × 2 возможно только при условии, что 
Примечания[править | править код]
- ↑ Кормен Т., Лейзерсон Ч., Ривест Р., Штайн К. Алгоритмы: построение и анализ, — М.: Вильямс, 2006 (с. 700).
- ↑ Petković, M. D. Generalized Schultz iterative methods for the computation of outer inverses (англ.) // Computers & Mathematics with Applications. — 2014. — June (vol. 67, iss. 10). — P. 1837—1847. — doi:10.1016/j.camwa.2014.03.019.
- ↑ Pan, V., Reif, J. Fast and efficient parallel solution of dense linear systems (англ.) // Computers & Mathematics with Applications. — 1989. — Vol. 17, iss. 11. — P. 1481—1491. — doi:10.1016/0898-1221(89)90081-3.
- ↑ Как найти обратную матрицу? mathprofi.ru. Дата обращения: 18 октября 2017. Архивировано 17 октября 2017 года.
Ссылки[править | править код]
- Реализация с полным выбором ведущего элемента на C++
В статье расскажем, что такое обратная матрица и обоснуем её основные свойства. Также рассмотрим несколько примеров с подробным решением, при помощи которых вы научитесь строить обратную матрицу для заданной.
Понятие обратной матрицы
Обратная матрица действует только для квадратных матриц с определителями, которые отличны от нуля. Это невырожденные матрицы
Обратная матрица лучше всего рассматривается на примере квадратной матрицы третьего порядка, которую по аналогии можно будет обобщить для матриц произвольного порядка.
Пусть
Квадратная матрица называется обратной матрицей этой
, если выполняется равенство:
(1)
тогда произведение этих матриц равняется единичной матрице
Давайте рассмотрим теорему на основании вышеописанных определений:
Если матрица – неособенная
тогда это условие необходимое и достаточное для существования обратной матрицы
Докажем необходимость:
Пусть у матрицы есть обратная матрица
, то есть
Согласно теореме про определитель произведения двух матриц получается:
так как
(2)
Достаточность. Пусть определитель матрицы не равен нулю, то есть
Сокращённо обозначим
Покажем, как найти обратную матрицу.
Для каждого из элементов матрицы
найдём соответствующие им алгебраические дополнения
=
: тогда
, разместив их в виде новой матрицы
соответственно расположению элементов
в
Получим:
(3)
Транспонируем матрицу , заменяя строки столбцами, получим формулу обратной матрицы:
=
=
(4)
При помощи теорем про раскладывание и аннулирование для определителей третьего порядка, несложно проверить, что
Нахождение обратной матрицы
Нужно найти обратную матрицу к матрице:
Решение будет в такой последовательности:
Шаг 1:
Вычислим определитель матрицы при помощи правила треугольников и получаем:
=
Как видите, , тогда существует обратная матрица:
Шаг 2:
Находим алгебраические дополнения элементов матрицы :
;
;
;
;
;
;
;
;
Шаг 3:
записываем новую матрицу по формуле (3):
Шаг 4:
По формуле (4) получим обратную матрицу:
=
=
=
Шаг 5:
Проверим, что
=
=
*
=
= =
=
=
=
В вышеописанном примере мы искали более сложную матрицу поэтапно. Давайте рассмотрим пример 2, который проще предыдущего.
Найти матрицу, обратную к матрице
Решение:
1)
2)
3)
4) =
*
5) =
*
*
=
*
=
= *
Содержание:
Теоремы существования и единственности обратной матрицы:
Рассмотрим квадратную матрицу:
Определение 4.1.1. Матрица, которая в результате умножения на матрицу А, равна единичной матрице Е, называется обратной А и обозначается
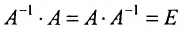
Отметим, что если А и В квадратные матрицы одного порядка, то определитель 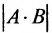
определителей множителей
Теорема 4.1.1. (теорема существования). Для существования обратной матрицы необходимо и достаточно, чтобы матрица А была невырожденной, т. е. чтобы 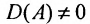
Доказательство. Необходимость. Пусть обратная матрица 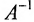
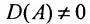
Так как обратная матрица существует, то 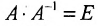
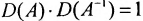
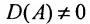
Достаточность. Пусть 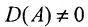
Вычислим алгебраические дополнения 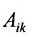
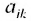
Матрица С называется союзной, или присоединенной, по отношению к матрице А, причем в i-й строке союзной матрицы С стоят алгебраические дополнения элементов i-го столбца матрицы А. Составим произведение матриц С и А, тогда элемент произведения, стоящий в i-й строке и k-м столбце, равен
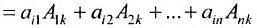
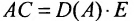
Так как 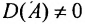
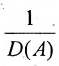
Тогда матрица 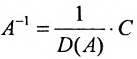
Сформулируем алгоритм нахождения обратной матрицы:.
- Вычислите определитель
исходной квадратной матрицы
- Если определитель равен нулю, то исходная матрица не имеет обратной; если определитель не равен нулю, то переходите ко второму шагу.
- Вычислите алгебраические дополнения элементов определителя исходной матрицы.
- Составьте присоединенную матрицу С, записав алгебраические дополнения элементов строк в столбцы.
- Умножьте элементы присоединенной матрицы на обратную величину определителя
исходной матрицы, тем самым постройте обратную матрицу
.
- Выполните проверку, т. е. рассмотрите произведение
или
. Должны получить единичную матрицу.
Этот алгоритм можно представить в виде следующей схемы:
Теорема 4.1.2. (теорема единственности). Для каждой неособенной матрицы А существует единственная обратная матрица.
Доказательство. Допустим, что наряду с обратной матрицей 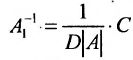
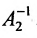
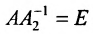
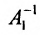
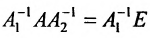
Поскольку 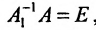
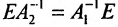
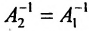
Вычислив определители левой и правой частей равенства 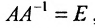
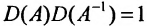
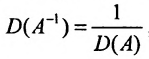
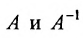
Замечание. Формула 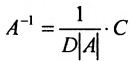
Свойства обратной матрицы. Подобная матрица
Укажем некоторые свойства обратной матрицы:
- Обратная матрица является невырожденной, т.е.
.
- Обратной матрице
будет матрица
.
- Обратная к транспонированной матрице равна транспонированной обратной матрице:
.
- Если матрица А симметрическая, то такой же будет обратная матрица:
.
- Матрица, обратная к произведению матриц, равна произведению обратных матриц, взятых в обратном порядке при условии, что обратные матрицы существуют:
.
- Если А такова, что обратная к ней матрица равна транспонированной матрице А, то говорят, что А – ортогональная матрица и
.
- Обратная для блочной квазидиагональной матрицы равна квазидиагональной матрице, состоящей из обратных матриц диагональных клеток:
Понятие обратной матрицы позволяет ввести следующее определение:
Определение 4.2.1. Квадратная матрица А называется подобной матрице В, если существует невырожденная матрица Т, для
которой выполняется равенство 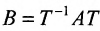
Говорят, что матрица А трансформируется в матрицу В при помощи матрицы Т.
Отношение подобия обладает тремя основными свойствами:
- а) рефлексивности: А подобна А;
- б) симметричности: если А подобна В, то и В подобна А;
- в) транзитивности: если А подобна В и В подобна С, то и А подобна С.
Приложения обратной матрицы в экономических исследованиях
Применение обратных матриц в экономических исследованиях столь многочисленно и разнообразно, что мы приведём отдельные примеры использования обратной матрицы в экономических исследованиях.
Пример:
Предположим, что затраты времени оборудования при выпуске изделий пропорциональны количеству готовых изделий и пусть известна квадратная матрица Т норм затрат времени оборудования на различные изделия на различных типах оборудования. Если задана матрица-столбец А затрат времени на различных типах оборудования, необходимое для выполнения производственной профаммы, то определение возможного выпуска готовых изделий X осуществляется с использованием обратной матрицы 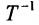
Валовой выпуск продукции X также можно определить, зная матрицу Z норм затрат рабочего времени рабочих различных категорий и фонд рабочего времени F по категориям рабочих, вычислив произведение обратной матрицы 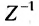
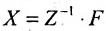
Пример:
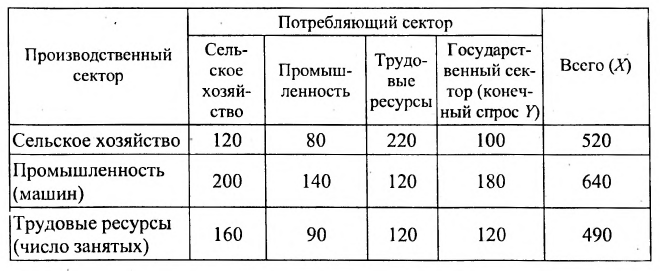
Рассмотрим четырёхсскторнос описание экономики, в котором выделены две отрасли: сельское хозяйство и промышленность, один первичный фактор производства – труд и государственный сектор, который потребляет продукцию обеих отраслей и использует труд. Государственный сектор ничего не производит для экономики и его потребление представляет собой конечный спрос на товары, производимые в этих секторах. В процессе производства каждая отрасль потребляет некоторое количество продукции другой, отрасли, а также труд; рабочая сила нуждается в продукции обеих отраслей и, наряду с этим, в затратах труда для своего воспроизводства. Трудовые ресурсы могут быть свободно импортированы и экспортированы, таким образом, никогда не может быть безработицы или излишнего спроса на труд. Основной капитал и запасы продукции поддерживаются на одном и том же уровне в течение всего периода. Наблюдая за потоками продукции между четырьмя секторами экономики составим таблицу «затраты-выпуск», табл.4.3.1.
Таблица 4.3.1
Сумма показателей в строках даёт общий выпуск каждой отрасли и суммарное число занятых. Суммы показателей по столбцам показывают затраты данного сектора, необходимые для производства всего объёма продукции. Следовательно, каждый столбец описывает производственную функцию данного сектора. Так, например, первый столбец характеризует основной производственный процесс, который в текущем периоде применяется в сельском хозяйстве. Для производства 520 т продукции сельского хозяйства требуется 120 т сельскохозяйственной продукции, 200 машин и 160 работников. Определим валовой выпуск продукции для конечного спроса, определяемого матрицей-столбцом: 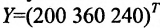
Решение:
Пусть 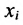
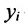
где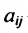
X = AX + Y, (4.3.1)
где X, Y- матрицы столбцы, а А- матрица коэффициентов прямых затрат. Все её элементы неотрицательны.
Воспользовавшись алгебраическими операциями над матрицами, перепишем уравнение (4.3.1) в виде: EX – АХ = Y, (E-A)X = Y. Умножив последнее матричное уравнение слева на обратную матрицу 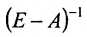
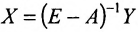
Следовательно, для определения валового выпуска продукции X в новом периоде нам нужно последовательно определить элементы матрицы А, Е-А и обратной матрицы 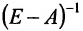
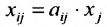
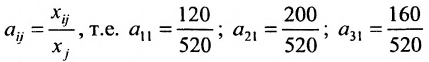
Далее вычисляем элементы матрицы Е-А:
вычисляем определитель
и алгебраические дополнения элементов матрицы (Е-А):
Составляем из алгебраических дополнений присоединённую матрицу С:
и вычисляем элементы обратной матрицы 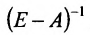
Тогда в силу (4.3) находим валовой выпуск продукции:
Таким образом, для удовлетворения новых показателей спроса необходимо будет произвести приблизительно 1042 т продукции сельского хозяйства, 1280 машин и нанять 1119 работников.
Особенности матриц в ценностном и натуральном выражении
Матрица коэффициентов прямых материальных затрат А, рассмотренная нами в примере предыдущего пункта, относится к классу неотрицательных матриц, так как матрица-столбец 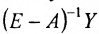
Определение 4.4.1. Если решение системы (4.3.1) сществует для любой неотрицательной матрицы Y конечного спроса, то матрица А называется продуктивной.
Поэтому элементы матрицы А не могут принимать произвольные положительные значения. Все диагональные элементы матрицы А должны быть меньше единицы. В противном случае производство лишается всякого смысла (если 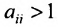
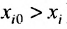
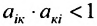
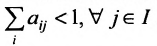
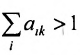
Так как норму матрицы А можно определить по формуле
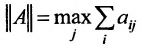
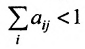
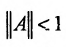
Если норма матрицы А меньше единицы, то
- 1)
;
- 2)
;
- 3)
;
- 4) все собственные
матрицы А по модулю меньше единицы, а наибольшее собственное значение положительно (теорема Фрабеииуса-Перропа);
- 5) все главные
матрицы (Е – А) положительны и меньше единицы.
Отметим, что в матрицах межотраслевого баланса в натуральном выражении условия 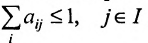
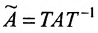
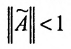
Подобные матрицы имеют равные по величине собственные значения и главные миноры;
Для продуктивности матрицы А необходимо и достаточно, чтобы выполнялось одно из приведенных ниже условий:
- Все главные миноры матрицы (Е – А) положительны и меньше единицы.
- Все собственные значения матрицы А по модулю меньше единицы.
- Матрица
полуположительна.
Условие 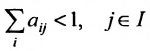
Матрица 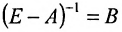
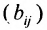
Коэффициенты полных затрат 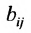
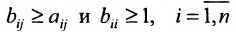
Вернёмся к примеру 1.12 и проанализируем матрицы коэффициентов прямых затрат А и полных затрат 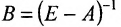
Элементы матрицы А удовлетворяют условиям:
4) норма матрицы
Значит матрица А является продуктивной и для неё существует обратная матрица 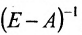
Из вида матрицы В следует, что все коэффициенты полных затрат 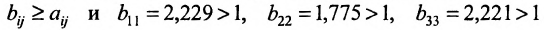
Определение обратной матрицы
Рассмотрим квадратную матрицу
Обозначим
Квадратная матрица А называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной, или особенной, если
Квадратная матрица В называется обратной для квадратной матрицы А того же порядка, если их произведение 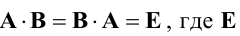
Теорема. Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля.
Матрица, обратная матрице А, обозначается через 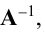
Обратная матрица вычисляется по формуле 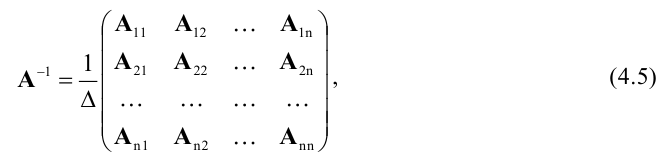
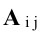
Вычисление обратной матрицы по формуле (4.5) для матриц высокого порядка очень трудоемко, поэтому на практике бывает удобно находить обратную матрицу с помощью метода элементарных преобразований (ЭП). Любую неособенную матрицу А путем ЭП только столбцов (или только строк) можно привести к единичной матрице Е. Если совершенные над матрицей А ЭП в том же порядке применить к единичной матрице Е, то в результате получится обратная матрица. Удобно совершать ЭП над матрицами А и Е одновременно, записывая обе матрицы рядом через черту. Отметим еще раз, что при отыскании канонического вида матрицы с целью нахождения ее ранга можно пользоваться преобразованиями строк и столбцов. Если нужно найти обратную матрицу, в процессе преобразований следует использовать только строки или только столбцы.
- Заказать решение задач по высшей математике
Пример:
Для матрицы 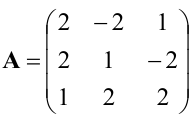
Решение:
Находим сначала детерминант матрицы А:
значит, обратная матрица существует и мы ее можем найти по формуле: 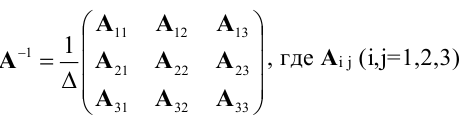
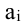
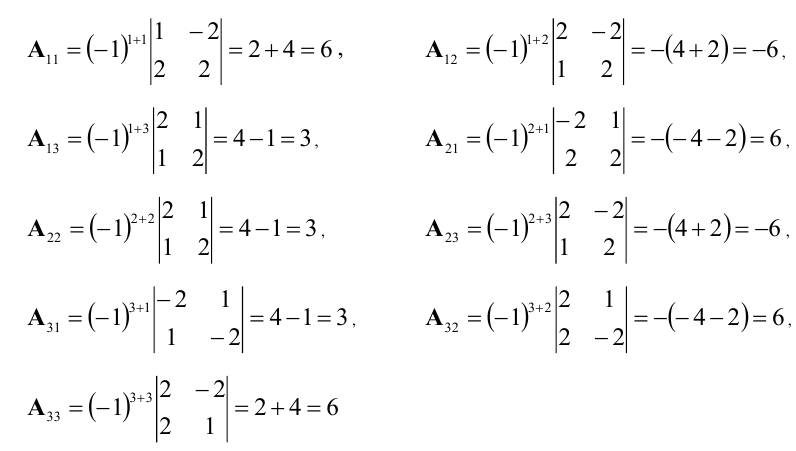
Пример:
Методом элементарных преобразований найти обратную матрицу для матрицы:
Решение:
Приписываем к исходной матрице справа единичную матрицу того же порядка:
С помощью элементарных преобразований столбцов приведем левую “половину” к единичной, совершая одновременно точно такие преобразования над правой матрицей. Для этого поменяем местами первый и второй столбцы:
К третьему столбцу прибавим первый, а ко второму – первый, умноженный на -2:
Из первого столбца вычтем удвоенный второй, а из третьего – умноженный на 6 второй;
Прибавим третий столбец к первому и второму:
Умножим последний столбец на -1:
Полученная справа от вертикальной черты квадратная матрица является обратной к данной матрице А. Итак,
Что такое обратная матрица и как её решать
Квадратная матрица, у которой все элементы вне главной диагонали равны нулю, называется диагональной.
Диагональная матрица, элементы 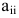
Пусть А – квадратная матрица порядка n. Матрица 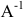
где Е – единичная матрица порядка n.
Внимание! Обратная матрица существует только для невырожденной квадратной матрицы.
Квадратная матрица, определитель которой отличен от нуля, называется невырожденной. В противном случае матрица называется вырожденной.
Теорема:
Для невырожденной матрицы 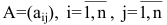
где 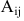
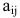
Пример:
Найти матрицу X из матричного уравнения АХ=В, где
Решение:
Умножим уравнение АХ=В на 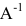
Найдем 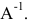
Вычислим алгебраические дополнения элементов матрицы А:
Следовательно,
Произведение матриц 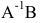
- Ранг матрицы – определение и вычисление
- Определители второго и третьего порядков и их свойства
- Метод Гаусса – определение и вычисление
- Прямая линия на плоскости и в пространстве
- Определённый интеграл
- Кратный интеграл
- Ряды в математике
- Дифференциальные уравнения с примерами











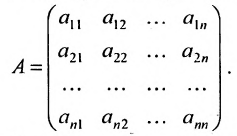
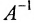
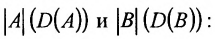
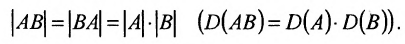
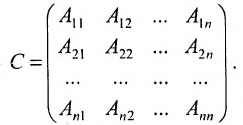
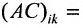
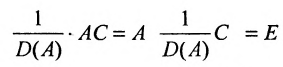
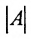 исходной квадратной матрицы
исходной квадратной матрицы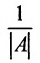 исходной матрицы, тем самым постройте обратную матрицу
исходной матрицы, тем самым постройте обратную матрицу 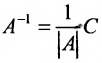 .
.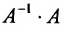 или
или 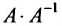 . Должны получить единичную матрицу.
. Должны получить единичную матрицу.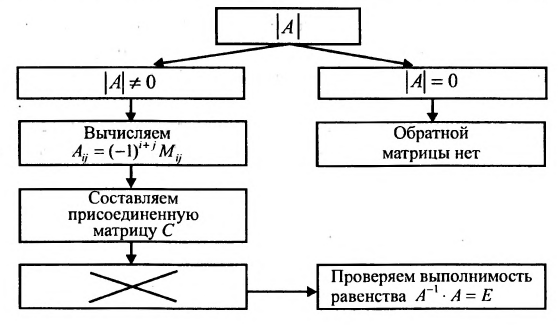
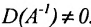 .
.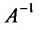 будет матрица
будет матрица 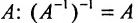 .
.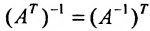 .
.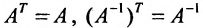 .
.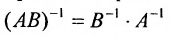 .
.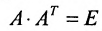 .
.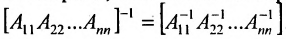
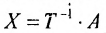
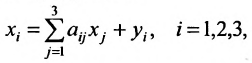


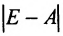

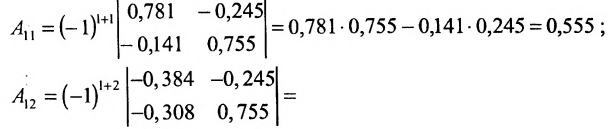

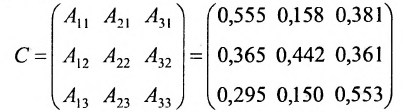

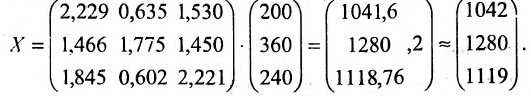
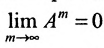 ;
;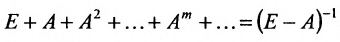 ;
;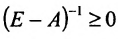 ;
;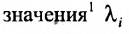 матрицы А по модулю меньше единицы, а наибольшее собственное значение положительно (теорема Фрабеииуса-Перропа);
матрицы А по модулю меньше единицы, а наибольшее собственное значение положительно (теорема Фрабеииуса-Перропа);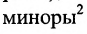 матрицы (Е – А) положительны и меньше единицы.
матрицы (Е – А) положительны и меньше единицы.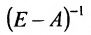 полуположительна.
полуположительна.