Взвешенный граф как найти вес ребра

Взвешенные графы

В классических графах все рёбра считаются равноценными и длина пути
соответствует количеству рёбер, которые он содержит. Однако часто
в задаче каждому ребру соответствует некоторый параметр – длина
ребра или стоимость прохождения по нему. В терминологии графов такой
параметр называется весом ребра, а граф, содержащий взвешенные
рёбра, взвешенным.

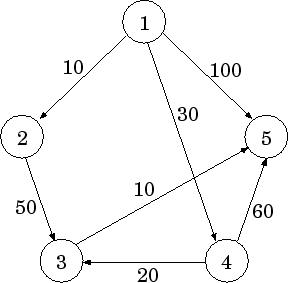
Типичная задача для таких графов – поиск кратчайшего пути. Например,
в этом графе кратчайший путь между вершинами (1) и (5): (1 – 4 – 3 – 5), так
как его вес равен (30 + 20 + 10 = 60), а вес ребра (1 – 5) равен (100).

Алгоритм Дейкстры

Классический алгоритм для поиска кратчайших путей во взвешенном графе –
алгоритм Дейкстры (по имени автора Эдгара Дейкстры). Он позволяет найти
кратчайший путь от одной вершины графа до всех остальных за (O(M log N))
((N, M) – количество вершин и рёбер соответственно).

Принцип работы алгоритма напоминает принцип работы BFS: на каждом шаге
обрабатывается ближайшая ещё не обработанная вершина (расстояние до неё
уже известно). При её обработке все ещё не посещённые соседи добавляются
в очередь для посещения (расстояние до каждой из них рассчитывается как
расстояние до текущей вершины + длина ребра). Главное отличие от BFS
заключается в том, что вместо классической очереди используется очередь с
приоритетом. Она позволяет нам выбирать ближайшую вершину за (O(log N)).

Анимация выполнения алгоритма Дейкстры для поиска кратчайшего пути из вершины
(a) в вершину (b):

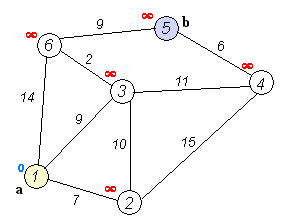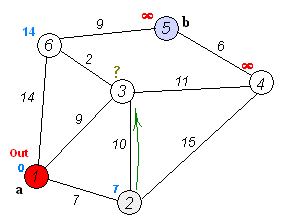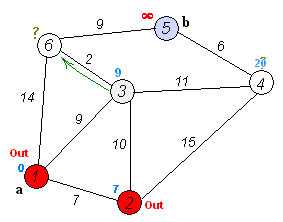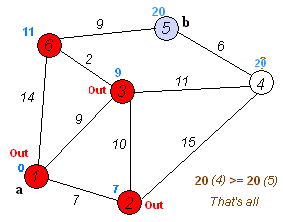
С помощью псевдокода алгоритм Дейкстры описывается следующим образом:

ans = массив расстояний от начальной вершины до каждой.
      изначально заполнен бесконечностями (ещё не достигнута).

ans[start] = 0

q = очередь с приоритетом, хранящая пары (v, dst),
    где dst - предполагаемое расстояние до v

добавить (start, 0) в q

пока q не пуста:
    (v, dst) = первая вершина в очереди (с минимальным расстоянием), и расстояние до неё
    извлечь (v, dst) из очереди

    если ans[v] < dst:   //мы уже обработали эту вершину, используя другой путь
        перейти к следующей вершине

    для каждой v -> u:
        n_dst = dst + len(v -> u)   //расстояние до u при прохождении через v
        если n_dst < ans[u]:        //если мы можем улучшить ответ
            ans[u] = n_dst
            добавить (u, n_dst) в q

Как видите, в очереди с приоритетом хранится не только номер вершины, но
и вычисленное расстояние до неё, по которому и ведётся сортировка. Также
возможна ситуация, при которой одна и та же вершина будет помещена в очередь
несколько раз с разным расстоянием (так как она достижима по нескольким рёбрам).
В такой ситуации обрабатываем её только один раз (с минимальным возможным
расстоянием).

Реализация

В нашей очереди с приоритетом должны храниться пары (вершина, расстояние до неё),
причём отсортированы они должны быть по уменьшению расстояния. Для этого нужно
использовать тип
std::priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>>:
первым элементом пары будет расстояние, а вторым – номер вершины.

Для хранения взвешенного графа в виде списка смежности для каждой вершины мы
храним вектор пар (соседняя вершина, длина ребра до неё).

Реализация на C++:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47



#include <bits/stdc++.h>

using namespace std;

const int INF = 1e9 + 7;

vector<pair<int, int>> graph[100000];
int ans[100000];

int main() {
    //Ввод графа и вершины start.

    for (int i = 0; i < n; i++) {
        ans[i] = INF;
    }

    ans[start] = 0;

    priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> q;

    q.push({0, start});

    while (!q.empty()) {
        pair<int, int> c = q.top();
        q.pop();

        int dst = c.first, v = c.second;

        if (ans[v] < dst) {
            continue;
        }

        for (pair<int, int> e: graph[v]) {
            int u = e.first, len_vu = e.second;

            int n_dst = dst + len_vu;
            if (n_dst < ans[u]) {
                ans[u] = n_dst;
                q.push({n_dst, u});
            }
        }
    }

    for (int i = 0; i < n; i++) {
        cout << "Shortest path from " << start + 1 << " to " << i + 1 << " has length " << ans[i] << endl;
    }
}






Реализация с восстановлением пути
Восстановление пути для алгоритма Дейкстры реализуется точно так же, как и для

BFS: при успешном улучшении пути в вершину (u) через вершину (v), мы запоминаем,

что (prev[v] = u). После окончания работы алгоритма используем массив (prev) для

восстановления пути в обратном направлении.
Реализация на C++:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64



#include <bits/stdc++.h>

using namespace std;

const int INF = 1e9 + 7;

vector<pair<int, int>> graph[100000];
int ans[100000];
int pr[100000];     //prev

int main() {
    //Ввод графа и вершин start и end.

    for (int i = 0; i < n; i++) {
        ans[i] = INF;
        pr[i] = -1;   //Значение, обозначающее что из этой вершины возвращаться некуда
    }

    ans[start] = 0;

    priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> q;

    q.push({0, start});

    while (!q.empty()) {
        pair<int, int> c = q.top();
        q.pop();

        int dst = c.first, v = c.second;

        if (ans[v] < dst) {
            continue;
        }

        for (pair<int, int> e: graph[v]) {
            int u = e.first, len_vu = e.second;

            int n_dst = dst + len_vu;
            if (n_dst < ans[u]) {
                ans[u] = n_dst;
                pr[u] = v;
                q.push({n_dst, u});
            }
        }
    }

    vector<int> path;

    int cur = end;
    path.push_back(cur);

    while (pr[cur] != -1) {
        cur = pr[cur];
        path.push_back(cur);
    }

    reverse(path.begin(), path.end());

    cout << "Shortest path between vertices " << start + 1 << " and " << end + 1 << " is: " << endl;

    for (int v: path) {
        cout << v + 1 << ", ";
    }
}






Область применения алгоритма Дейкстры
Алгоритм Дейкстры является оптимальным для поиска пути практически в любых

графах, но он имеет одно ограничение. Алгоритм Дейкстры неприменим для графов,

содержащих рёбра с отрицательным весом. Для поиска кратчайшего пути в таких

графах обычно используют алгоритм Форда-Беллмана.

Все, что познается, имеет число, ибо невозможно ни понять ничего, ни познать без него – Пифагор

В этой статье:

Матрица смежности

Матрица инцидентности

Список смежности (инцидентности)

Взвешенный граф (коротко)

Итак, мы умеем задавать граф графическим способом. Но есть еще два способа как можно задавать граф, а точнее представлять его. Для экономии памяти в компьютере граф можно представлять с помощью матриц или с помощью списков.

Матрица является удобной для представления плотных графов, в которых число ребер близко к максимально возможному числу ребер (у полного графа).

Другой способ называется списком. Данный способ больше подходит для более разреженных графов, в котором число ребер намного меньше максимально возможного числа ребер (у полного графа).

Перед чтением материала рекомендуется ознакомится с предыдущей статьей, о смежности и инцидентности, где данные определения подробно разбираются.

Матрица смежности

Но тем кто знает, но чуть забыл, что такое смежность есть краткое определение.

Смежность – понятие, используемое только в отношении двух ребер или в отношении двух вершин: два ребра инцидентные одной вершине, называются смежными; две вершины, инцидентные одному ребру, также называются смежными. 

Матрица (назовем ее L) состоит из n строк и n столбцов и поэтому занимает n^2 места.  

Каждая ячейка матрицы равна либо 1, либо 0;

Ячейка в позиции L (i, j) равна 1 тогда и только тогда, когда существует ребро (E) между вершинами (V) i и j. Если у нас положение (j, i), то мы также сможем использовать данное правило. Из этого следует, что число единиц в матрице равно удвоенному числу ребер в графе. (если граф неориентированный). Если ребра между вершинами i и j не существует, то ставится 0.

Для практического примера возьмем самый обыкновенный неориентированный граф:

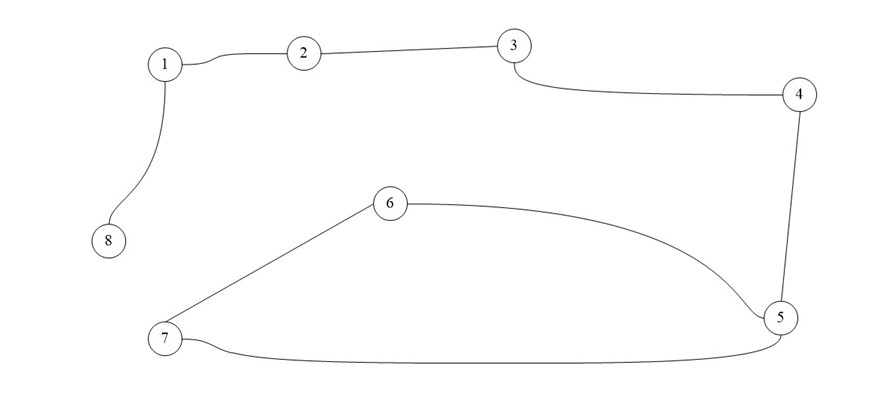
А теперь представим его в виде матрицы:

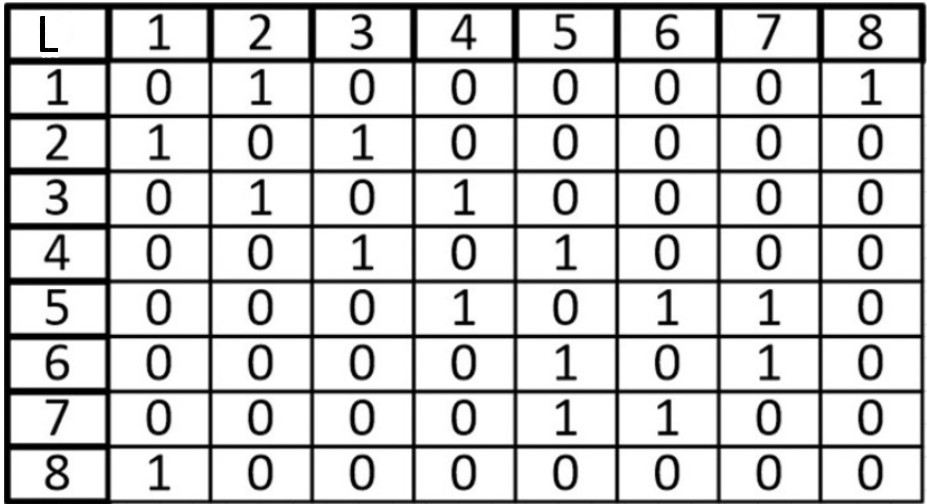
Ячейки, расположенные на главной диагонали всегда равны нулю, потому что ни у одной вершины нет ребра, которое и начинается, и заканчивается в ней только если мы не используем петли. То есть наша матрица симметрична относительно главной диагонали. Благодаря этому мы можем уменьшить объем памяти, который нам нужен для хранения.

С одной стороны объем памяти будет:

Но используя вышеописанный подход получается:

Потому что нижнюю часть матрицы мы можем создать из верхней половины матрицы. Только при условии того, что у нас главная диагональ должна быть пустой, потому что при наличии петель данное правило не работает.

Если граф неориентированный, то, когда мы просуммируем строку или столбец мы узнаем степень рассматриваемой нами вершины.

Если мы используем ориентированный граф, то кое-что меняется.

Здесь отсутствует дублирование между вершинами, так как если вершина 1 соединена с вершиной 2, наоборот соединена она не может быть, так у нас есть направление у ребра.

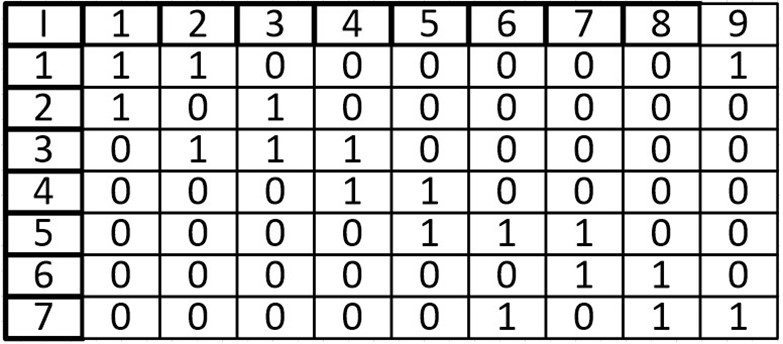
Возьмем в этот раз ориентированный граф и сделаем матрицу смежности для него:

В виде матрицы:

Если мы работаем со строкой матрицы, то мы имеем элемент из которого выходит ребро, в нашем случаи вершина 1 входит в вершину 2 и 8. Когда мы работаем со столбцом то мы рассматриваем те ребра, которые входят в данную вершину. В вершину 1 ничего не входит, значит матрица верна.

Объем памяти:

Если бы на главной диагонали была бы 1, то есть в графе присутствовала петля, то мы бы работали уже не с простым графом, с каким мы работали до сих пор.

Используя петли мы должны запомнить, что в неориентированном графе петля учитывается дважды, а в ориентированном – единожды.

Матрица инцидентности

Инцидентность – понятие, используемое только в отношении ребра и вершины: две вершины (или два ребра) инцидентными быть не могут.

Матрица (назовем ее I) состоит из n строк которое равно числу вершин графа, и m столбцов, которое равно числу ребер. Таким образом полная матрица имеет размерность n x m. То есть она может быть, как квадратной, так и отличной от нее.

Ячейка в позиции I (i, j) равна 1 тогда, когда вершина инцидентна ребру иначе мы записываем в ячейку 0, такой вариант представления верен для неориентированного графа.

Сразу же иллюстрируем данное правило:

В виде матрицы:

Сумма элементов i-ой строки равна степени вершины.

При ориентированным графе, ячейка I (i, j) равна 1, если вершина V (i) начало дуги E(j) и ячейка I (i, j) равна -1 если вершина V (i) конец дуги E (j), иначе ставится 0.

Ориентированный граф:

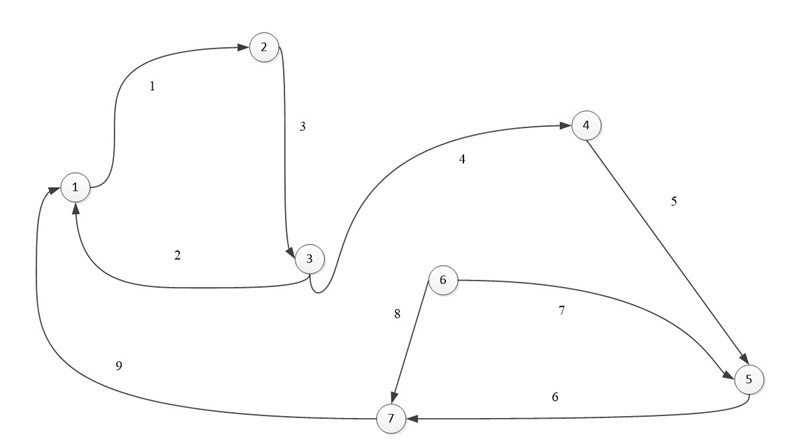
В виде матрицы:

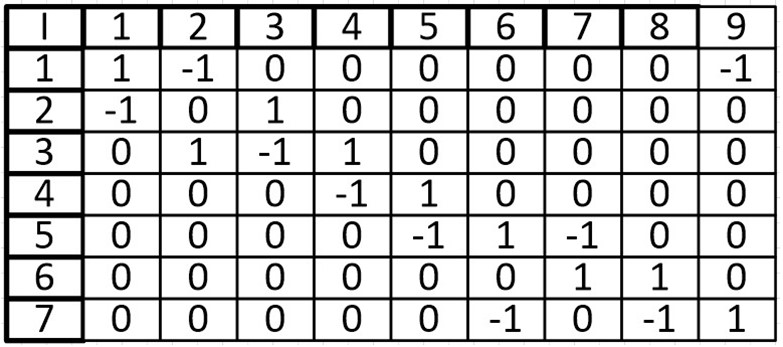
Одной из особенностей данной матрицы является то, что в столбце может быть только две ненулевых ячейки. Так как у ребра два конца.

При суммировании строки, ячейки со значением -1, могут складываться только с ячейками, также имеющими значение -1, то же касается и 1, мы можем узнать степень входа и степень выхода из вершины. Допустим при сложении первой вершины, мы узнаем, что из нее исходит 1 ребро и входят два других ребра. Это является еще одной особенностью (при том очень удобной) данной матрицы.

Объем памяти:

Список смежности (инцидентности)

Список смежности подразумевает под собой, то что мы работаем с некоторым списком (массивом). В нем указаны вершины нашего графа. И каждый из них имеет ссылку на смежные с ним вершины.

В виде списка это будет выглядеть так:

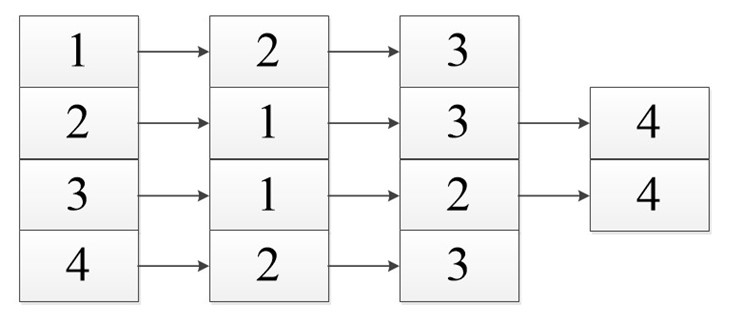
Неважно в каком порядке вы расположите ссылку так как вы рассматриваете смежность относительно первой ячейки, все остальные ссылки указывают лишь на связь с ней, а не между собой.

Так как здесь рассматривается смежность, то здесь не обойдется без дублирования вершин. Поэтому сумма длин всех списков считается как:

Объем памяти:

Когда мы работаем с ориентированным графом, то замечаем, что объем задействованной памяти будет меньше, чем при неориентированном (из-за отсутствия дублирования).

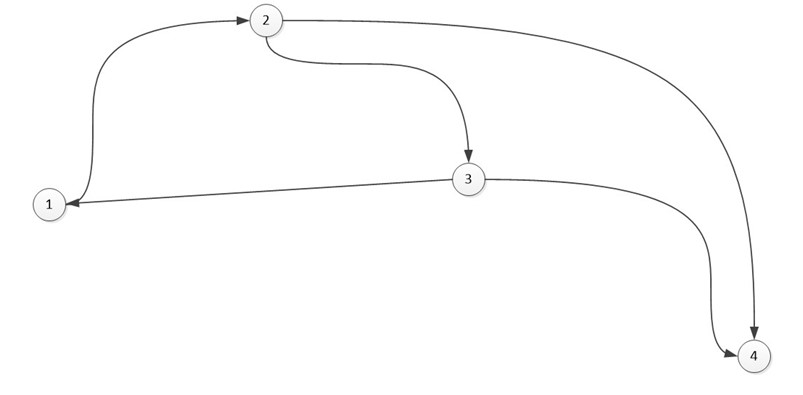
В виде списка:

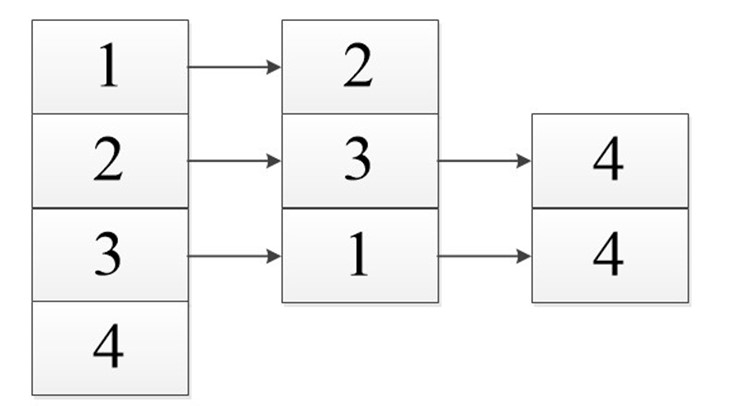
Сумма длин всех списков:

Объем памяти:

Со списком инцидентности все просто. Вместо вершин в список (массив) вы вставляете рёбра и потом делаете ссылки на те вершины, с которыми он связан.

К недостатку списка смежности (инцидентности) относится то что сложно определить наличие конкретного ребра (требуется поиск по списку). А если у вас большой список, то удачи вам и творческих успехов! Поэтому, чтобы работать максимальной отдачей в графе должно быть мало рёбер.

Взвешенность графа

Взвешенный граф – это граф, в котором вместо 1 обозначающее наличие связи между вершинами или связи между вершиной и ребром, хранится вес ребра, то есть определённое число с которым мы будем проводить различные действия.

К примеру, возьмем граф с весами на ребрах:

И сделаем матрицу смежности:

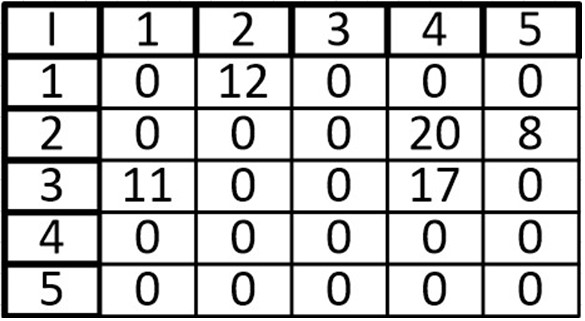
В ячейках просто указываем веса ребра, а в местах где отсутствует связь пишем 0 или -∞.

Более подробно данное определение будет рассмотрено при нахождении поиска кратчайшего пути в графе.

Итак, мы завершили разбор представления графа с помощью матрицы смежности и инцидентности и списка смежности (инцидентности). Это самые известные способы представления графа. В дальнейшем мы будем рассматривать и другие матрицы, и списки, которые в свою очередь будут удобны для представления графа с определёнными особенностями.

Если заметили ошибку или есть предложения пишите в комментарии.

На каком языке программирования проводить операции с графами

Проголосовали 47 пользователей.

Воздержались 8 пользователей.

При необходимости
дополнительной информации о вершинах
и рёбрах, используются взвешенные
графы.

Если каждому ребру
графа приписано некоторое положительное
число, то такое число называется весом,
а сам граф называется взвешенным
графом.

Четвёрка <V,
E,
f,
g>
называется взвешенным
графом,
когда для вершины v
элемент f(v)
– вес вершины,
а для ребра e
элемент g(е)
– вес ребра.

Информацию
о весах рёбер во взвешенном графе
представляют с помощью матрицы весовW=w_ij
,

Пример
7.8.
Схема
автомобильных дорог с указанием их
протяжённости будет
описана матрицей весов:

7.7. Упорядочивание вершин и дуг орграфа.

Расчеты в задачах,
связанных с графами, заметно упрощаются,
если их элементы упорядочены. Под
упорядочиванием вершин
связного орграфа без циклов понимают
такое разбиение его вершин на группы,
при котором:

1) вершины первой
группы не имеют предшествующих вершин,
а вершины последней группы последующих;

2) вершины любой
другой группы не имеют предшествующих
в следующей группе;

3) вершины одной
и той же группы дугами не соединяются.

Аналогичным
образом вводится понятие упорядочения
дуг. В
результате упорядочения элементов
получают орграф, изоморфный исходному.

Упорядочение
элементов выполняется графическим или
матричным способом.

Графический способ
упорядочивание вершин, дуг орграфа
носит название алгоритма
Фалкерсона.

Алгоритм Фалкерсона для упорядочения вершин:

1. Находят вершины
графа, в которые не входит ни одна дуга.
Они образуют первую группу. Нумеруют
вершины группы в натуральном порядке
1, 2, … . При этом присвоение номеров
вершинам внутри группы может быть
сделано не единственным образом, что
не имеет значения.

2. Вычеркиваем все
пронумерованные вершины и дуги, из них
выходящие. В получившемся графе найдется,
по крайней мере, одна вершина, в которую
не входит ни одна дуга. Этим вершинам,
входящим во вторую группу, присваивается
очередной номер и т.д. Повторяем до тех
пор, пока все вершины не будут упорядочены
(пронумерованы).

Алгоритм Фалкерсона для упорядочения дуг:

1. Найти дуги, не
имеющие непосредственно предшествующих
(они образуют I
группу).

2. Вычеркнуть
найденные дуги; после этого появится,
по крайней мере, одна новая дуга, не
имеющая непосредственно предшествующей
(в графе без дуг I
группы). Такие дуги составляют II
группу. Повторять этот шаг, пока все
дуги не будут разбиты на группы. В
заключение упорядочения дугам присваивают
новые обозначения с индексами 1, 2, … .

Пример 7.11.
Графическим способом упорядочить
вершины и дуги заданного орграфа.

Решение.
Используя алгоритм Фалкерсона,
упорядочим вершины и дуги заданного
орграфа.

Вершина b
называется достижимой
из вершины а, если существует (a,b)-путь.

Пусть A – матрица
смежностей ориентированного графа G.

Элемент на
пересечении i-й строки и j-го столбца
матрицы Aⁿ
равен
количеству путей длины n из i-й вершины
в j-ю вершину.

Получив матрицу
Bⁿ=A+A²+…+Aⁿ,
можно определить количество
путей из v_i
в v_j
длины, меньшей или равной n.

Пусть G=(V,E) –
ориентированный граф, содержащий n
вершин. Матрица P размерности n x n,
элементы которой задаются выражением

называется
матрицей
достижимости
(путевой матрицей) графа G.

Соседние файлы в папке Лекции_2

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Разберем несколько причин, почему граф

, который строит алгоритм Крускала, действительно остовное дерево графа:

Теперь рассмотрим, почему у дерева Крускала

— минимальный вес. Представим минимальное расходящееся дерево

, которое не равно

. Когда мы проходим через процесс Крускала и добавляем ребра, мы добавляем в

ребро

, которое не является частью

.

Предположим, мы попытаемся добавить

в

. Это создаст цикл по основным свойствам деревьев. Вдоль этого цикла должно быть еще какое-то ребро

, которого нет в

.

— это дерево, и оно не может содержать все ребра этого цикла.

В этом примере показана гипотетическая часть

вместе с

и

:

Теперь удалим

из

и заменим его на

— это дерево

. Если просто менять одно ребро цикла на другое,

все равно прямое дерево

.

Процесс Крускала добавил ребро

, а не

. Это означает, что вес

меньше или равен весу

. Это делает

минимальным прямым деревом

, которое согласуется с

на одно ребро больше, чем

.

Мы можем повторять этот процесс, пока не получим минимальное остовное дерево, которое согласуется с

по каждому ребру. Это означает, что

должно быть минимальным остовным деревом.

Информатика. Учебник для 9 класса (по учебнику К. Ю. Полякова, Е.А. Еремина, базовый уровень) 

§17. Графы.

---

Что такое граф?

Ключевые слова:

• граф	
• вершина	
• ребро	
• матрица смежности	
• степень вершины	
• связный граф
• взвешенный граф
• весовая матрица
• ориентированный граф
• оптимальный путь
• количество путей

Давайте подумаем, как можно наглядно представить такую информацию:

От пос. Васюки три дороги идут в Солнцево, Грибное и Ягодное. Между Солнцевом и Грибным и между Грибным и Ягодным также есть дороги. Кроме того, есть дорога, которая идет из Грибного в лес и возвращается обратно в Грибное.
Нарисуйте в тетради схему дорог по этому описанию.

Можно, например, нарисовать такую схему (рис. 3.17, а).

Рис. 3.17

В информатике для исследования таких схем используют графы.

Граф — это набор вершин (узлов) и связей между ними — рёбер.

Граф, соответствующий нашей схеме дорог, показан на рис. 3.17, б, для краткости населённые пункты обозначены латинскими буквами.

Матрица смежности графа

Для хранения информации об узлах и связях показанного выше графа можно использовать таблицу такого вида (рис. 3.18).

Рис. 3.18

Единица на пересечении строки А и столбца В означает, что между вершинами А и В есть связь. Ноль указывает на то, что связи нет. Такая таблица называется матрицей смежности. Она симметрична относительно главной диагонали (см. закрашенные клетки в таблице).

Исследуйте матрицу смежности и сравните её с графом на рис. 3.17, б. Что означает единица на пересечении столбца С и строки С?

В этом графе есть петля — ребро, которое начинается и заканчивается в одной и той же вершине.

Степенью вершины называют количество рёбер, с которыми связана вершина. При этом петля считается дважды (с вершиной связаны оба конца ребра!).

Подсчитайте по матрице смежности, сколько ребёр в графе. Определите степени всех вершин. Как вы рассуждали?

Строго говоря, граф — это математический объект, а не рисунок. Конечно, его можно нарисовать на плоскости (например, как на рис. 3.17, б), но матрица смежности не даёт никакой информации о том, как именно располагать вершины друг относительно друга. Для таблицы, приведённой выше, возможны, например, такие варианты (рис. 3.19).

Рис. 3.19

Нарисуйте по матрице смежности (рис. 3.20) два разных изображения графа.

Рис. 3.20

Граф имеет 4 вершины, причём каждая вершина связана рёбрами со всеми остальными. Нарисуйте этот граф. Сколько всего рёбер в этом графе?

Граф имеет N вершин, причём каждая вершина связана рёбрами со всеми остальными. Сколько всего рёбер в этом графе?

Граф имеет 4 ребра. Чему равна сумма степеней вершин в этом графе? Зависит ли она от количества вершин?

Граф имеет N рёбер. Чему равна сумма степеней вершин в этом графе?

Попробуйте нарисовать граф с пятью вершинами, где все вершины имеют степень 3. Получилось ли у вас? Почему?

Связный граф

В графе на рис. 3.17, б все вершины связаны: между любой парой вершин существует путь — последовательность вершин, в которой каждая следующая связана ребром с предыдущей. Такой граф называется связным.

Связный граф — это граф, между любыми вершинами которого существует путь.

Теперь представьте себе, что дороги Васюки-Солнцево, Васю- ки-Грибное и Грибное-Ягодное завалило снегом (или размыло дождём) так, что по ним ни пройти, ни проехать (рис. 3.21).

Рис. 3.21

Эту схему тоже можно считать графом (она соответствует определению), но в таком графе есть две несвязанные части, каждая из которых — связный граф. Такие части называют компонентами связности.

Постройте матрицу смежности графа, изображённого на рис. 3.21.

Граф имеет 4 вершины и две компоненты связности. Какое наибольшее количество рёбер может быть в этом графе, если в нём нет петель? Нарисуйте этот граф.

Вспоминая материал предыдущего параграфа, можно сделать вывод, что дерево — это частный случай связного графа. Но у него есть одно важное свойство — в дереве нет замкнутых путей — циклов, т. е. путей, которые начинаются и заканчиваются в одной и той же вершине.

Найдите все циклы в графе на рис. 3.17.

Дерево — это связный граф, в котором нет циклов.

Взвешенный граф

Если в нашем примере нас заинтересует не только наличие дорог между посёлками, но ещё и расстояния между ними, каждой связи нужно сопоставить число — вес ребра (рис. 3.22).

Рис. 3.22

Взвешенный граф — это граф, с каждым ребром которого связано некоторое число — вес ребра.

Весом может быть не только расстояние, но и, например, стоимость проезда или другая величина.

Как хранить информацию о таком графе? Ответ напрашивается сам собой — нужно в таблицу записывать не 1 или 0, а вес ребра. Если связи между двумя узлами нет, на бумаге можно оставить ячейку таблицы пустой, а при хранении в памяти компьютера записывать в неё условный код, например, число -1 или очень большое число. Такая таблица называется весовой матрицей, потому что содержит веса рёбер. В данном случае она выглядит так (рис. 3.23).

Рис. 3.23

Так же как и матрица смежности, весовая матрица симметрична относительно диагонали.

Что означают пустые ячейки в весовой матрице?

Как по весовой матрице сразу определить, сколько рёбер в графе?

Определите по весовой матрице (рис. 3.24) длины путей ADBEC, ABDCE, DEBAC. Как вы рассуждали?

Рис. 3.24

Оптимальный путь в графе

Для того чтобы определить оптимальный (наилучший) путь между двумя вершинами графа, нужно ввести какой-то числовой показатель, по которому можно сравнивать пути — определять, какой из них лучше. Обычно для оценки пути используют сумму весов ребёр, входящих в этот путь. Например, при поиске кратчайшего пути чем меньше это значение, тем лучше.

Какие показатели вы используете в жизни для определения оптимального пути? Всегда ли самый короткий путь — самый лучший?

Если в графе немного узлов, по весовой матрице можно легко определить оптимальный путь из одной вершины в другую простым перебором вариантов. Рассмотрим граф, заданный весовой матрицей на рис. 3.25 (числа определяют стоимость поездки между соседними пунктами).

Рис. 3.25

Найдём наилучший путь из А в В — такой, при котором общая стоимость поездки минимальная.

Для решения задачи будем строить дерево перебора вариантов. Видим, что из пункта А напрямую

Рис. 3.26

Числа около рёбер обозначают стоимость поездки по этому участку, а индексы у названий узлов показывают общую стоимость проезда в данный узел из узла А. Теперь разберём варианты дальнейшего движения из узла С I tM lt;pb р (рис. 3.27).

Рис. 3.27

Почему, на ваш взгляд, на схеме не показана возможность движения из С в А?

Видим, что из С сразу можно попасть в В, стоимость проезда в этом случае равна 7.

Почему нельзя на этом остановиться, ведь путь из А в В найден?

Проверяя пути через узел В, выясняем, что можно сократить стоимость до 6 (рис. 3.28)

Рис. 3.28

Нужно ли исследовать дальше путь, содержащий цепочку ACED? Сравните стоимость этого пути и стоимость уже найденного пути из А в В.

Аналогично строим вторую часть схемы (рис. 3.29).

Рис. 3.29

Таким образом, оптимальный (наилучший) путь — ADEB, его стоимость — 3.

Нужно ли проверять пути ACED и ADEC, не дошедшие до узла В? Могут ли они улучшить результат?

Конечно, для более сложных графов метод перебора работает очень долго, поэтому используются более совершенные (но значительно более сложные) методы.

Ориентированный граф

Наверное, вы заметили, что при изображении деревьев, которые описывают иерархию (подчинение), мы ставили стрелки от верхних уровней к нижним. Это означает, что для каждого ребра указывается направление, и двигаться можно только по стрелкам, но не наоборот.

Ориентированный граф (орграф) — это граф, в котором каждое ребро имеет направление.

Орграф может служить, например, моделью системы дорог с односторонним движением. Матрица смежности и весовая матрица для орграфа уже не обязательно будут симметричными.

На схеме на рис. 3.30 всего две дороги с двусторонним движением, по остальным можно ехать только в одну сторону.

Рис. 3.30

Рёбра в орграфе называют дугами. Дуга, в отличие от ребра, имеет начало и конец.

Нарисуйте граф по весовой матрице, показанной на рис. 3.31. С помощью дерева перебора найдите все возможные пути из вершины А в вершину Е, не проходящие дважды через одну и ту же вершину, и стоимости проезда по каждому из этих путей. Определите оптимальный путь из вершины А в вершину Е.

Рис. 3.31

---

Количество путей

Определим количество возможных путей из вершины А в вершину К для ориентированного графа, показанного на рис. 3.32.

Рис. 3.32

Так как граф ориентированный, переходить в другую вершину можно только по стрелкам.

В графе на рис. 3.32 есть одна начальная вершина А, из которой дуги только выходят. Такая вершина называется истоком. Вершина, в которую дуги только входят (и ни одна не выходит), называется конечной вершиной или стоком. В нашем графе сток — это вершина К.

По весовой матрице на рис. 3.31 найдите исток и сток в графе. Как вы рассуждали?

Будем двигаться по стрелкам от начальной вершины А. Около каждой вершины запишем количество возможных путей из вершины А в эту вершину. В вершину А существует единственный путь — пустой (никуда не ехать). Найдём все вершины, в которые можно приехать только из А: это вершины Б и Г, записываем около них количество путей 1 (рис. 3.33).

Рис. 3.33

Теперь ищем вершины, в которые можно попасть только из уже отмеченных вершин. Например, в вершину В есть один путь из А напрямую, а также по одному пути через Б и Г (так как эти вершины отмечены числом 1). Общее количество путей из А в Б равно сумме отметок предыдущих вершин: для вершины В получаем 3 пути. В вершину Ж можно попасть только из Г, поэтому число путей в Г и Ж совпадает (рис. 3.34).

Рис. 3.34

В вершину Д идёт один путь через Б и три пути через В, поэтому общее число путей — 4. Аналогично получаем 4 пути в вершину Е: 3 пути через В и один через Ж (рис. 3.35).

Рис. 3.35

Далее находим один путь из А в И (только через Ж) и 4 пути из А в 3 (все через Д). В конечную вершину К можно приехать через вершины Д (4 пути), 3 (4 пути), Е (4 пути) и И (1 путь), таким образом, общее количество различных путей равно 13 (рис. 3.36).

Рис. 3.36

---

Выводы

• Граф — это набор вершин (узлов) и связей между ними — рёбер.
• Матрица смежности — это таблица, в которой единица на пересечении строки и столбца обозначает ребро между соответствующими вершинами, а ноль — отсутствие ребра.
• Связный граф — это граф, между любыми вершинами которого существует путь.
• Цикл — это замкнутый путь в графе.
• Дерево — это связный граф, в котором нет циклов.
• Взвешенный граф — это граф, с каждым ребром которого связано некоторое число — вес ребра. Взвешенный граф описывается весовой матрицей.
• Ориентированный граф (орграф) — это граф, в котором каждое ребро имеет направление. Рёбра орграфа называют дугами. Матрица смежности и весовая матрица орграфа могут быть несимметричными.

Нарисуйте в тетради интеллект-карту этого параграфа.

---

Вопросы и задания

1. Можно ли сказать, что лес (множество деревьев) — это граф? Почему?
2. Как по матрице смежности определить, есть ли петли в графе?
3. Как по весовой матрице определить длину пути в графе?
4. Когда для представления данных используются орграфы? Приведите примеры.
5. Выполните по указанию учителя задания в рабочей тетради.

---

Оглавление

§16. Списки и деревья.

§17. Графы.

§18. Игровые стратегии.

---