Параметры параболы
Точка F(p/2, 0) называется фокусомпараболы, величина p – параметром, точка О(0, 0) – вершиной (рис. 9.15). При этом прямая OF, относительно которой парабола симметрична, задает ось этой кривой.

Величина 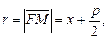 где M(x, y) – произвольная точка параболы, называется фокальным радиусом, прямая D: x = –p/2 – директрисой (она не пересекает внутреннюю область параболы). Величина
где M(x, y) – произвольная точка параболы, называется фокальным радиусом, прямая D: x = –p/2 – директрисой (она не пересекает внутреннюю область параболы). Величина 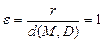 называется эксцентриситетомпараболы.
называется эксцентриситетомпараболы.
Основное характеристическое свойство параболы: все точки параболы равноудалены от директрисы и фокуса (рис. 9.15).
Существуют иные формы канонического уравнения параболы, которые определяют другие направления ее ветвей в системе координат (рис. 9.16):
а) 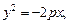 б)
б) 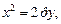 в)
в) 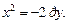

Для параметрического задания параболы в качестве параметра t может быть взята величина ординаты точки параболы:
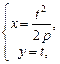
где t – произвольное действительное число.
Пример 1.Определить параметры и форму параболы по ее каноническому уравнению:
1) 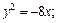 2)
2) 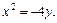
Решение.1) Уравнение y 2 = –8x определяет параболу с вершиной в точке О(0; 0), симметричную относительно оси Оx. Ее ветви направлены влево. Сравнивая данное уравнение с уравнением y 2 = –2px, находим: 2p = 8, p = 4, p/2 = 2. Следовательно, фокус находится в точке F(–2; 0), уравнение директрисы D: x = 2 (рис. 9.17).
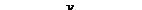
2) Уравнение x 2 = –4y задает параболу с вершиной в точке O(0; 0), симметричную относительно оси Oy. Ее ветви направлены вниз. Сравнивая данное уравнение с уравнением x 2 = –2py, находим: 2p = 4, p = 2, p/2 = 1. Следовательно, фокус находится в точке F(0; –1), уравнение директрисы D: y = 1 (рис. 9.18).

Пример 2.Определить параметры и вид кривой x 2 + 8x – 16y – 32 = 0. Сделать рисунок.
Решение. Преобразуем левую часть уравнения, используя метод выделения полного квадрата:
(x + 4) 2 – 16 – 16y – 32 = 0;
В результате получим:
Это каноническое уравнение параболы с вершиной в точке (–4; –3), параметром p = 8, ветвями, направленными вверх 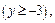 осью x = –4. Фокус находится в точке F(–4; –3 + p/2), т. е. F(–4; 1) Директриса D задается уравнением y = –3 – p/2 или y = –7 (рис. 9.19).
осью x = –4. Фокус находится в точке F(–4; –3 + p/2), т. е. F(–4; 1) Директриса D задается уравнением y = –3 – p/2 или y = –7 (рис. 9.19).
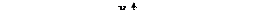
Пример 3. Написать уравнение кривой, все точки которой равноудалены от прямой y = –3 и точки F(0; 3).
Решение. Точка F(0; 3) лежит на оси Oy и находится с прямой y = –3 по разные стороны от начала координат, причем на одинаковом расстоянии (d = 3). Это позволяет заключить, что искомой кривой является парабола x 2 = 2py с параметром p = 2 × 3 = 6, т. е. x 2 = 12y (рис. 9.20).
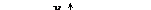
Пример 4.Составить уравнение параболы с вершиной в точке V(3; –2) и фокусом в точке F(1; –2).
Решение. Вершина и фокус данной параболы лежат на прямой, параллельной оси Ox (одинаковые ординаты), ветви параболы направлены влево (абсцисса фокуса меньше абсциссы вершины), расстояние от фокуса до вершины равно p/2 = 3 – 1 = 2, p = 4. Следовательно, искомое уравнение
Дата добавления: 2015-09-29 ; просмотров: 8094 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Уравнения с параметрами.
Исследование и решение уравнений с параметрами считается не самым простым разделом школьной математики. Однако, параметр, как понятие, часто воспринимается школьниками гораздо более сложным, чем есть в действительности. Здесь в первом пункте представлены очень простые вводные примеры использования параметров в уравнениях. Те, для кого это понятие не составляет большой трудности, могут сразу перейти к решению задач, которые представлены ниже.
Что такое уравнение с параметром?
Допустим нам нужно решить уравнение 2х + 5 = 2 − x.
Решение: 2x + x = 2 − 5; 3x = −3; x = −3/3 = −1.
Теперь нужно решить уравнение 2x + 5 = 3 − x.
Решение: 2x + x = 3 − 5; 3x = −2; x = −2/3
Затем нужно решить уравнение 2x + 5 = 0,5 − x.
Решение: 2x + x = 0,5 − 5; 3x = −4,5; x = −4,5/3 = −1,5.
А потом может потребоваться решить уравнение 2x + 5 = 10,7 − x или уравнение 2x + 5 = −0,19 − x.
Понятно, что уравнения похожи, а потому их решение будет сопровождаться теми же действиями, что выше. Возникает естественный вопрос – сколько можно делать одно и то же?
Уменьшим себе трудозатраты. Заметим, что все эти уравнения отличаются только одним числом в правой части. Обозначим это число символом a .
Получим уравнение 2х + 5 = a − х,
где a – переменная величина, вместо которой можно подставить нужное числовое значение и получить нужное уравнение. Эта переменная и называется параметром.
Решим это уравнение так же, как и все предыдущие.
Решение: 2х + 5 = a − x; 2x + x = a − 5; 3x = a − 5; x = (a − 5)/3.
Теперь для того, чтобы найти ответы для двух последних примеров, мы можем не повторять полностью всё решение каждого уравнения, а просто подставить в полученную формулу для х числовое значение параметра а:
x = (10,7 − 5)/3 = 5,7/3 = 1,9;
x = (−0,19 − 5)/3 = −5,19/3 = −1,73.
Таким образом, под термином “уравнение с параметром”, фактически, скрывается целое семейство “почти одинаковых уравнений” , которые отличаются друг от друга только одним числом (одним слагаемым или одним коэффициентом) и одинаково решаются. Параметр – это число, которое меняется от уравнения к уравнению.
Полученную формулу для корня уравнения мы можем запрограммировать на компьютере. Достаточно будет только ввести значение параметра a, чтобы получить решение любого такого уравнения.
Рассмотрим еще один пример.
Замечаем, что они похожи друг на друга и отличаются только первым коэффициентом. Обозначим его, например, символом k.
Решим уравнение kх + 5 = 2 − x с параметром k.
С помощью этой формулы вычислим все ответы для приведенных уравнений.
x = −3/(2 + 1) = −1
x = −3/(3 + 1) = −0,75
x = −3/(−4 + 1) = 1
x = −3/(17 + 1) = −1/6
Можем ли мы теперь запрограммировать эту формулу и сказать, что с её помощью можно решить любое аналогичное уравнение?
Запрограммировать можем. Компьютер справится как с очень большими значениями коэффициента, так и с очень маленькими.
Например, если введём k = 945739721, то для уравнения заданного вида будет получен корень примерно равный −0,0000000031721201195353831188, если k = 0,0000004, то получим корень ≈ −2,9999988000004799998080000768.
Но, если мы введем в программу, казалось бы, более простое значение k = −1, то компьютер зависнет.
Почему?
Посмотрим внимательнее на формулу x = −3/(−1 + 1) = −3/0. Деление на ноль.
Посмотрим на соответствующее уравнение −1·х + 5 = 2 − x.
Преобразуем его −х + x = 2 − 5.
Оказывается, оно равносильно уравнению 0 = −3 (. ) и не может иметь корней.
Таким образом, из общего подхода к решению “почти одинаковых уравнений” могут существовать исключения, о которых нужно позаботиться отдельно. Т.е. провести предварительное исследование всего семейства уравнений. Именно этому и учатся на уроках математики с помощью так называемых задач с параметрами.
Графические способы решения уравнений
Сначала вспомним, что представляет собой графический способ решения обычного уравнения (без параметра).
Пусть дано уравнение вида f(x) = g(x) . Построим графики функций y = f(x) и y = g(x) и найдём точки пересечения этих графиков. Абсциссы точек пересечения и есть корни уравнения.
Для быстрого построения эскизов графиков повторите еще раз графики элементарных функций, которые изучаются в школьном курсе математики, и правила преобразования графиков функций.
Рассмотрим примеры.
1. Решить уравнение
2х + 5 = 2 − x

Ответ: x = −1.
2. Решить уравнение
2х 2 + 4х − 1 = 2х + 3

3. Решить уравнение
log2х = −0,5х + 4

Ответ: x = 2.
Первые два из приведенных уравнений вы можете решить и аналитически, так как это обычные линейное и квадратное уравнения. Второе уравнение содержит функции разных классов – степенную (здесь линейную) и трансцендентную (здесь логарифмическую). Для таких случаев выбор способов решения у школьников очень ограничен. Фактически, единственным доступным способом является именно графическое решение.
Внимание: Для корней, найденных графическим способом, обязательна проверка! Вы уверены, что на третьем рисунке пересечение именно в точке х = 4 , а не в точке 3,9 или 4,1? А если на реальном экзамене у вас нет возможности построить график достаточно точно? На чертеже “от руки” разброс может быть еще больше. Поэтому алгоритм действий должен быть следующим:
- Предварительный вывод: х ≈ 4.
- Проверка: log24 = −0,5·4 + 4; 2 = −2 + 4; 2 ≡ 2.
- Окончательный вывод х = 4.
Чтобы графически решать уравнения с параметрами надо строить не отдельные графики, а их семейства.
Решение уравнений с параметрами с помощью графиков.
Задача 1.
Найти все значения параметра q при которых уравнение |x + 1| − |x − 3| − x = q 2 − 8q + 13 имеет ровно 2 корня.
При каждом значении параметра q можно вычислить значение выражения q 2 − 8q + 13 . Результат обозначим переменной а.
Т.е. примем q 2 − 8q + 13 = a и решим уравнение с параметром |x + 1| − |x − 3| − x = a
Строим график функции y = |x + 1| − |x − 3| − x , расположенной в левой части уравнения.
Для этого разобьём числовую ось на отрезки точками, в которых каждый из встречающихся модулей принимает нулевое значение.

Для каждого из этих участков раскроем модули с учётом знаков.
Вспомним: по определению |x| = x, если х ≥ 0, и |x| = −x, если х Чтобы проверить знаки модулей на участке достаточно подставить любое промежуточное значение x из этого отрезка, например, −2, 0 и 4.
Таким образом на участке I, где −∞ имеем −(x + 1) + (x − 3) − x = − x − 4.
Следовательно, должны построить график функции y = − x − 4 .
Это линейная функция. Её график прямая линия, которую можно построить по двум точкам, например, x = 0, y = −4 и у = 0, x = −4. Cтроим всю прямую бледной линией, а затем выделяем часть графика, относящуюся только к рассматриваемому участку.
Аналогично, разбираемся с оставшимися двумя участками.
На участке II, где −1 имеем (x + 1) + (x − 3) − x = x − 2
и должны построить соответствующую часть графика функции y = x − 2 .
На участке III, где 3 , имеем (x + 1) − (x − 3) − x = − x + 4
и должны построить соответствующую часть графика функции y = − x + 4 .
Последовательное построение итогового графика показано ниже. (Чтобы увеличить рисунок, нужно щелкнуть по нему левой кнопкой мыши.)
Замечание: если вы освоили тему Преобразование графиков функций, то с этой частью задачи сможете справиться быстрее, чем показано в примере.
Итак, построение графика функции, расположенной в левой части уравнения, мы завершили. Посмотрим, что находится в правой части.
График функции y = a представляет собой прямую линию, параллельную оси абсцисс (Ox), и пересекающую ось ординат (Oy) в точке а. Так как а – параметр, который может принимать разные значения, то нужно построить целое семейство таких параллельных линий, пересекающих ось ординат на разной высоте. Очевидно, что все графики семейства построить мы не сможем, поскольку их бесконечное множество. Изобразим для примера несколько штук в районе уже построенного графика функции. Ниже прямые семейства y = a показаны красным цветом.
Из рисунка видно, что количество точек пересечения каждой из красных прямых с ранее построенным (зелёным) графиком зависит от высоты, на которой расположена эта прямая, т.е. от параметра а. Прямые, расположенные ниже y = −3 , пересекают график в одной точке, а значит эти уравнения имеют только одно решение. Прямые, проходящие на уровне −3 имеют по три точки пересечения, значит соответствующие уравнения будут иметь по три решения. Прямые, расположенные выше точки y = 1 , снова имеют только по одной точке пересечения.
Ровно две точки пересечения с зелёным графиком будут иметь только прямые y = 1 и y = −3 . Соответствующие уравнения будут иметь ровно два корня, что и требовалось определить в задании.
Однако мы нашли значения введённого нами параметра а, при котором заданное уравнение имеет 2 корня, а вопрос задачи состоял в том, чтобы найти все значения параметра q. Для этого придётся решить следующую совокупность уравнений: 
Это обычные квадратные уравнения, которые решаются через дискриминант или по теореме Виета. 
Таким образом, окончательный ответ: <2;4;6>.
Задача 2.
Найти все значения параметра a, при которых уравнение (2 − x)x(x − 4) = a имеет ровно 3 корня.
Рассмотрим функцию y = (2 − x)x(x − 4) . Видно, что если раскрыть скобки, то старший член будет −х 3 . Т.е. графиком функции должна быть кубическая парабола, причем на при x, стремящемcя к +∞, y → −∞, а при x, стремящемся к −∞, y → +∞.
Поскольку уравнение (2 − x)x(x − 4) = 0 имеет три корня 2, 0 и 4, то график функции будет пересекать ось абсцисс трижды.
Понятно, что при упомянутых условиях график непрерывной функции должен иметь участок с “волной”. Строим от руки эскиз графика.
Правая часть уравнения y = a такая же, как в предыдущей задаче. Поэтому дальнейшие построения не требуют комментариев. Смотрите рисунки. Чтобы увеличить, используйте щелчок мышью.






Из рисунков видно, что прямые, отделяющие линии с тремя точками пересечения от других случаев, проходят через экстремумы кубической функции. Поэтому определяем значения ymax и ymin через производную. (Исследовать функцию полностью не нужно, так как примерное положение точек экстремума мы видим на эскизе графика.) Обратите внимание на то, что при вычислении значений функции используются точные значения x и формулы сокращенного умножения. Приближенные значения в промежуточных вычислениях не используют.
Ответ: 
Задача для самостоятельного решения
Задача 3.
При каком наибольшем отрицательном значении параметра а уравнение  имеет один корень?
имеет один корень?
Ответ: -1,625
Задача реального экзамена ЗНО-2013 (http://www.osvita.ua/).
Переход на главную страницу сайта “Математичка”.

Есть вопросы? пожелания? замечания?
Обращайтесь – mathematichka@yandex.ru
Внимание, ©mathematichka. Прямое копирование материалов на других сайтах запрещено. Ставьте гиперссылку.
Примеры решений: кривые второго порядка
В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости на тему Кривые второго порядка: приведение к каноническому виду, нахождение характеристик, построение графика т.п.
Кривые 2-го порядка: решения онлайн
Задача 1. Привести к каноническому виду уравнение кривой 2 порядка, найти все ее параметры, построить кривую.
Задача 2. Дана кривая. Привести к каноническому виду. Построить и определить вид кривой.
Задача 3. Выяснить вид кривой по общему уравнению, найти её параметры и положение в системе координат. Сделать рисунок.
Задача 4. Общее уравнение кривой второго порядка привести к каноническому. Найти координаты центра, координаты вершин и фокусов. Написать уравнения асимптот и директрис. Построить линии на графики, отметить точки.
Задача 5. Дана кривая $y^2+6x+6y+15=0$.
1. Докажите, что данная кривая – парабола.
2. Найдите координаты ее вершины.
3. Найдите значения ее параметра $р$.
4. Запишите уравнение ее оси симметрии.
5. Постройте данную параболу.
Задача 6. Дана кривая $5x^2+5y^2+6xy-16x-16y=16$.
1. Докажите, что эта кривая – эллипс.
2. Найдите координаты центра его симметрии.
3. Найдите его большую и малую полуоси.
4. Запишите уравнение фокальной оси.
5. Постройте данную кривую.
Задача 7. Найти уравнения параболы и её директрисы, если известно, что парабола имеет вершину в начале координат и симметрична относительно оси $Ox$ и что точка пересечения прямых $y=x$ и $x+y-2=0$ лежит на параболе.
Задача 8. Составить уравнение кривой, для каждой точки которой отношение расстояния до точки $F(0;10)$ к расстоянию до прямой $x=-4$ равно $sqrt<2/5>$. Привести это уравнение к каноническому виду и определить тип кривой.
Задача 9. Даны уравнения асимптот гиперболы $y=pm 5x/12$ и координаты точки $M(24,5)$, лежащей на гиперболе. Составить уравнение гиперболы.
Задача 10. Даны уравнение параболы $y=1/4 x^2+1$ и точка $C(0;2)$, которая является центром окружности. Радиус окружности $r=5$.
Требуется найти
1) точки пересечения параболы с окружностью
2) составить уравнение касательной и нормали к параболе в точках её пересечения с окружностью
3) найти острые углы, образуемые кривыми в точках пересечения. Чертёж.
[spoiler title=”источники:”]
http://mathematichka.ru/school/parametry/param_equation.html
http://www.matburo.ru/ex_ag.php?p1=agk2
[/spoiler]
Сообщения без ответов | Активные темы
| Автор | Сообщение | |||
|---|---|---|---|---|
|
||||
|
Пожалуйста, помогите с такой задачей. Как такое делается, решается? Найти параметр [math]p[/math] параболы [math]{y^2} = 2px[/math], если известно, что эта парабола проходит через точки пересечения прямой [math]y = x[/math] с окружностью [math]{x^2} + {y^2} – 6x = 0[/math].
|
|||
| Вернуться к началу |
|
|||
|
The_Blur |
|
||
|
Почему система?
|
|||
| Вернуться к началу |
|
||
|
Alexdemath |
Заголовок сообщения: Re: Найти параметр “p” параболы
|
|
The_Blur писал(а): Почему система? Да, и всё.
|
|
| Вернуться к началу |
|
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Найти уравнение параболы
в форуме Аналитическая геометрия и Векторная алгебра |
dadessm |
15 |
447 |
20 дек 2018, 11:55 |
|
Найти уравнение параболы
в форуме Аналитическая геометрия и Векторная алгебра |
ArsPol |
1 |
669 |
25 окт 2013, 19:36 |
|
Как найти дуги параболы
в форуме Интегральное исчисление |
brom |
3 |
306 |
05 апр 2017, 22:34 |
|
Найти пересечение параболы и окружности
в форуме Геометрия |
ferma-T |
11 |
386 |
10 апр 2022, 10:30 |
|
Найти каноническое уравнение параболы
в форуме Аналитическая геометрия и Векторная алгебра |
MYNAME |
14 |
524 |
18 ноя 2017, 11:14 |
|
Найти координаты точки параболы
в форуме Аналитическая геометрия и Векторная алгебра |
hahahacker |
4 |
199 |
10 ноя 2021, 21:17 |
|
Найти расстояние от точки до параболы
в форуме Исследование операций и Задачи оптимизации |
whit3_1 |
9 |
363 |
13 ноя 2021, 15:11 |
|
Найти массу дуги параболы
в форуме Интегральное исчисление |
Irina123 |
2 |
1443 |
19 июн 2018, 15:05 |
|
Найти каноническое уравнение параболы
в форуме Аналитическая геометрия и Векторная алгебра |
Zqquiet |
5 |
245 |
07 дек 2020, 17:32 |
|
Найти координаты фокусов,уравнение директрисы параболы
в форуме Аналитическая геометрия и Векторная алгебра |
norogen |
5 |
11810 |
27 июн 2013, 11:48 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 5 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Координаты фокуса параболы: как найти, формула
Содержание:
- Формулировка параболы в алгебре и геометрии
- Что такое фокус параболы, определение
-
Как найти фокус параболы
- Уравнение расчета
- Чему равны координаты фокуса
- Абсцисса фокуса параболы
- Примеры расчета фокусного расстояния в задачах
Формулировка параболы в алгебре и геометрии
Определение
Парабола — совокупность точек на плоскости, расположенных на одинаковом удалении от фокуса F и директрисы d, в которую точка F не входит.
Парабола является коническим сечением, или коникой. Это значит, что она возникает при пересечении плоскости с поверхностью кругового конуса. Плоскость сечения при этом параллельна одной из касательных плоскостей конуса.
Точка пересечения параболы с ее осью называется вершиной. Она считается началом системы координат, канонической для данной кривой.
Что такое фокус параболы, определение
Определение
Расстояние от точки фокуса до любой точки параболы равняется расстоянию от этой точки к директрисе.
Если в фокус поместить источник света, все исходящие из него световые лучи после отражения от нее пойдут по прямым, параллельным оси симметрии. И наоборот, все световые лучи, идущие параллельно оси, после отражения от «стенок» кривой соберутся в одной точке. Это оптическое свойство широко применяется в конструкциях прожекторов, фар, фонарей, телескопов-рефлекторов.
Как найти фокус параболы
Уравнение расчета
Каноническое уравнение:
(y^2;=;2px)
Если расположить параболу слева от оси ординат, уравнение примет вид:
(y^2;=;-;2px)
Параметр p — расстояние от фокуса до директрисы, которая определяется уравнением:
(х;=;-frac p2)
Чтобы узнать расстояние r от любой точки параболы до фокуса, равное ее расстоянию до директрисы, нужно воспользоваться формулой:
(r;=;frac p2;+;x)
В полярной системе координат с центром в фокусе и направлением вдоль оси фокальный параметр можно найти по формуле:
(p;=;rho;times;(1;+;cosleft(varthetaright)))
Чему равны координаты фокуса
Фокус будет иметь координаты ((frac p2;;0)).
Абсцисса фокуса параболы
Также фокус и параметр p можно искать через так называемую фокальную хорду (Р_1Р_2).
Эта прямая, проходящая через фокус и параллельная директрисе, пересекает параболу в двух точках. Половина длины фокальной хорды будет равна параметру p, являясь абсолютной величиной ординаты любой из точек (Р_1, Р_2).
Абсцисса каждой из этих точек будет равна абсциссе фокуса (frac p2).
Для ординаты y каждой из точек (Р_1, Р_2):
(y^{2;}=;2p;times;frac p2;=;p^2).
Примеры расчета фокусного расстояния в задачах
Пример 1
Определить координаты фокуса параболы (y^{2;}=;4х).
Решение
Находим параметр p:
4 = 2p
p = 2
Координаты (1; 0).
Пример 2
Определить координаты фокуса параболы (y^{2;}=;6х).
Решение
Находим параметр p:
6 = 2p
p = 3
Координаты (1,5; 0).
Насколько полезной была для вас статья?
Рейтинг: 2.02 (Голосов: 47)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Сперва найдем точки пересечения прямой у=х и окружности х^2+y^2-6*x=0, для чего подставим у из уравнения прямой в уравнение окружности. Получим
x^2+x^2-6*x=0, откуда х=0 и х=3. Соответственно в этих точках из уравненя прямой получим у=0 и у=3. Подставляя координаты точек пересечения в уравнение параболы, получим, что через точку(0;0) парабола проходит при любых р, а в точке (3;3) уравнение параболы примет вид 3^2=2*р*3, откуда р=1.5
1,5 K
Комментировать ответ…Комментировать…
Ответы на похожие вопросы
Парабола — это график функции описанный определённой формулой. Чтобы построить параболу нужно следовать формуле, определениям и уравнениям.
Парабола
Парабола – это множество точек плоскости, которые равноотделённые от заданной точки, что называется фокусом и заданной прямой под названием директриса.
Чтобы получить каноническое уравнение параболы, расположим директрису перпендикулярно оси , а фокус
на оси
так, чтобы начало координат
помещался на одинаковом расстоянии от них (см. рис. 1). Обозначим через
расстояние от фокуса к директрисе, тогда у фокуса будут координаты
,
.
Для произвольной точки параболы расстояний
, а расстояние к директрисе
. По определению
из рис. 1 видим, что
, а
и поэтому:
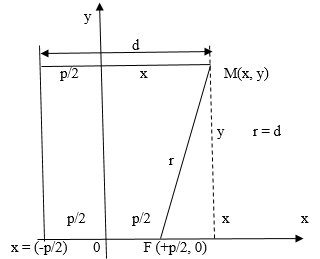
Рис. 1
(1)
– каноническое уравнение параболы.
Нужна помощь в написании работы?

Мы – биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Заказать работу
Что такое вершина параболы
Вершина параболы – это парабола, которая проходит через точки . Если точка
принадлежит параболе, то и
тоже принадлежит параболе, так как из:
.
Значит, парабола симметрична относительно оси , её график достаточно построить в первой четверти, где из канонического уравнения параболы получается, что:
Чтобы найти вершину параболы, необходимо знать формулу: .
Давайте посмотрим, как данная формула действует, допустим дано уравнение:
Тогда:
,
,
. Чтобы найти величины
,
и
, в квадратном уравнении коэффициент при
, при
, постоянная (коэффициент без переменной) =
. Если взять тот же пример,
, получается, что:
,
,
.
Форма и характеристики параболы
Исследуем за каноническим уравнением форму и расположение параболы:
1. В уравнении переменная входит в парной степени откуда получается, что парабола симметрична относительно оси
. Ось
– это ось, которая симметрична параболе.
2. Так как , тогда
, откуда получается, что парабола расположена справа от оси
.
3. При мы имеем
, то есть парабола проходит через начало координат. Точка
– это вершина параболы.
4. При увеличении значений переменной модуль
тоже возрастает. Изобразим параболу на рисунке:
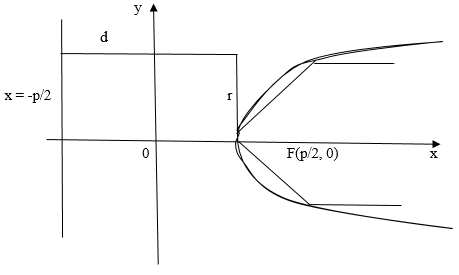
Рис. 2
5. В полярной системе координат, у канонического уравнения параболы такой вид:
6. Уравнение ,
,
, тоже описывают параболы:
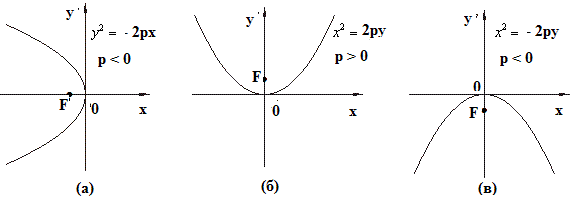
Рис. 3
Оптическое свойство параболы
У параболы “оптическое” свойство, если: в фокусе параболы поместить источник света, тогда отбитые от параболы лучи будут параллельными оси . Это свойство учитывают при изготовлении прожекторов, зеркальных телескопов, теле- и радио антенн.
При положительном уравнении:
описывают параболу симметричную относительно с вершиной в точке
, ветви которой направлены влево (рис. 3 (а)).
Аналогично изложенному, уравнение и
описывают параболы с вершиной в точке
симметрично относительно
, ветви которой направлены соответственно вверх и вниз (см. рис. 3 (б) и (в)). Если например, уравнение
решить относительно
и обозначить
, тогда получим известное со школьного курса уравнение параболы
. Теперь её фокусное расстояние
.
Примеры решения
Задача
Найти координаты фокуса и составить уравнение директрисы параболы .
Решение
Сравнивая каноническое уравнение и данное
, получим
,
, тогда
. Так как уравнение директрисы
, тогда в данном случае
.
Ответ
координаты фокуса: , а уравнение директрисы параболы:
.
Задача
Составить каноническое уравнение параболы:
а) с фокусом в точке ;
б) с фокусом в точке .
Решение
а). Так как фокус на положительной полуоси
, тогда парабола симметрична относительно
с вершиной в точке
и
, поэтому
и согласно формуле (1)
.
б). Фокус лежит на отрицательной полуоси
с вершиной в точке
, ветви направлены вниз, каноническое уравнение следует искать в виде
. Фокусное расстояние параболы
и уравнение запишется
.
Ответ
а) каноническое уравнение параболы с фокусом в точке :
;
б) каноническое уравнение с фокусом в точке :
.
Задача
Показать путём выделения полного квадрата, что уравнение – это уравнение параболы. Привести его к каноническому виду. Найти вершину, фокус, ось и директрису этой параболы.
Решение
Выделим относительно переменной полный квадрат
=
=
=
=
=
=
.
Обозначим ,
. Тогда в результате параллельного переноса координатных осей в новое начало, то есть в точку
, получим каноническое уравнение параболы
.
Ветви этой параболы направлены вниз симметрично относительно оси ,
,
– фокусное расстояние. В новой системе координат фокус находится в точке
, уравнение директрисы в новой системе
.
Повернёмся к старым координатам при помощи замены ,
. Уравнение оси в новой системе
, а в старой
– уравнение оси параболы.
Уравнение директрисы в новой системе координат , а в старой
.
В новой системе для фокуса
,
, а в старой системе
,
, то есть
.
Ответ
Каноническое уравнение параболы – ;
вершина – ветви параболы направлены вниз;
,
,
– фокусное расстояние, а фокус находится в точке
;
уравнение оси ;
уравнение директрисы .




