
Всех приветствую, решал накануне задачки по этой теме и 2 из них получились с корявым ответом((( Так и должно быть или где-то что-то попутал??
Освещенность, получаемая при нормальном падении солнечных лучей на поверхность Земли около 1.0 * 10^5 лк. Считая, что излучение Солнца подчиняется закону Ламберта и пренебрегая поглощением света в атмосфере, определить яркость Солнца,если известно, что радиус земной орбиты 1,5*10^8 км, а диаметр Солнца 1,4*10^6 км.
Решал вот как
И того получилось
З.Ы. тут в правилах прочитал, что одна тема – один вопрос, относится ли то же к задачам? Можно ли написать вторую задачу в этой теме или нужно создать новую?

Звёздная величина Солнца и Луны
Продолжим нашу алгебраическую экскурсию к небесным светилам. В той шкале, которая применяется для оценки блеска звёзд, могут, помимо неподвижных звёзд; найти себе место и другие светила – планеты, Солнце, Луна. О яркости планет мы побеседуем особо; здесь же укажем звёздную величину Солнца и Луны. Звёздная величина Солнца выражается числом минус 26,8, а полной1) Луны – минус 12,6. Почему оба числа отрицательные, читателю, надо думать, понятно после всего сказанного ранее. Но, быть может, его приведёт в недоумение недостаточно большая разница между звёздной величиной Солнца и Луны: первая «всего вдвое больше второй».
Не забудем, однако, что обозначение звёздной величины есть, в сущности, некоторый логарифм (при основании 2,5). И как нельзя, сравнивая числа, делить один на другой их логарифмы, так не имеет никакого смысла, сравнивая между собой звёздные величины, делить одно число на другое. Каков результат правильного сравнения, показывает следующий расчёт.
Если звёздная величина Солнца «минус 26,8», то это значит, что Солнце ярче звезды первой величины
в 2,527,8 раза. Луна же ярче звезды первой величины
в 2,513,6 раза.
Значит, яркость Солнца больше яркости полной Луны в
2,527,8 2,514,2 раза. 2,513,6
Вычислив эту величину (с помощью таблиц логарифмов), получаем 447 000. Вот, следовательно, правильное отношение яркостей Солнца и Луны: дневное светило в ясную погоду освещает Землю в 447 000 раз сильнее, чем полная Луна в безоблачную ночь.
Считая, что количество теплоты, отбрасываемое Луной, пропорционально количеству рассеиваемого ею света, – а это, вероятно, близко к истине, – надо признать, что Луна посылает нам и теплоты в 447 000 раз меньше, чем Солнце. Известно, что каждый квадратный сантиметр на границе земной атмосферы получает от Солнца около 2 малых калорий теплоты в 1 минуту. Значит, Луна посылает на 1 см2 Земли ежеминутно не более 225 000-й доли малой калории (т. е. может нагреть 1 г воды в 1 минуту на 225 000-ю часть градуса). Отсюда видно, насколько не обоснованы все попытки приписать лунному свету какое-либо влияние на земную погоду2).
1)В первой и в последней четверти звёздная величина Луны минус 9.
2)Вопрос о том, может ли Луна влиять на погоду своим притяжением, будет рассмотрен в конце книги (см. «Луна и погода»).
120
Распространённое убеждение, что облака нередко тают под действием лучей полной Луны, – грубое заблуждение, объясняемое тем, что исчезновение облаков в ночное время (обусловленное другими причинами) становится заметным лишь при лунном освещении.
Оставим теперь Луну и вычислим, во сколько раз Солнце ярче самой блестящей звезды всего неба – Сириуса. Рассуждая так же, как и раньше, получаем отношение их блеска:
|
2,527,8 |
2,525,2 |
10 000 000 000. |
|
2,52,6 |
т. е. Солнце ярче Сириуса в 10 миллиардов раз.
Очень интересен также следующий расчёт: во сколько раз освещение, даваемое полной Луной, ярче совокупного освещения всего звёздного неба, т. е. всех звёзд, видимых простым глазом на одном небесном полушарии? Мы уже вычислили, что звёзды от первой до шестой величины включительно светят вместе так, как сотня звёзд первой величины. Задача, следовательно, сводится к вычислению того, во сколько раз Луна ярче сотни звёзд первой величины.
Это отношение равно
2,513,6
100 2700.
Итак, в ясную безлунную ночь мы получаем от звёздного неба лишь 2700-ю долю того света, какой посылает полная Луна, и в 2700×447 000, т. е. в 1200 миллионов раз меньше, чем даёт в безоблачный день Солнце.
Прибавим ещё, что звёздная величина нормальной международной
«свечи» на расстоянии 1 м равна минус 14,2, значит, свеча на указанном расстоянии освещает ярче полной Луны в 2,514,2-12,6 т. е. в четыре раза.
Небезынтересно, может быть, отметить ещё что прожектор авиационного маяка силой в 2 миллиарда свечей виден был бы с расстояния Луны звездой 4½-й величины, т. е. мог бы различаться невооружённым глазом.
Истинный блеск звёзд и Солнца
Все оценки блеска, которые мы делали до сих пор, относились только к их видимому блеску. Приведённые числа выражают блеск светил на тех расстояниях, на каких каждое из них в действительности находится. Но мы хорошо знаем, что звёзды удалены от нас неодинаково; видимый блеск звёзд говорит нам поэтому как об их истинном блеске, так и об их удалении от нас, – вернее, ни о том, ни о другом, пока мы не расчленим оба фактора. Между тем важно знать, каков был бы сравнительный блеск или, как говорят, «светимость» различных звёзд, если бы они находились от нас на одинаковом расстоянии.
Ставя так вопрос, астрономы вводят понятие об «абсолютной» звёздной величине звёзд. Абсолютной звёздной величиной звезды называется та, которую звезда имела бы, если бы находилась от нас на рас-
121

стоянии 10 «парсеков». Парсек – особая мера длины, употребляемая для звёздных расстояний; о её происхождении мы побеседуем позднее особо, здесь скажем лишь, что один парсек составляет около 30 800 000 000 000 км. Самый расчёт абсолютной звёздной величины произвести нетрудно, если знать расстояние звезды и принять во внимание, что блеск должен убывать пропорционально квадрату расстояния1).
Мы познакомим читателя с результатом лишь двух таких расчётов: для Сириуса и для нашего Солнца. Абсолютная величина Сириуса +1,3, Солнца +4,8. Это значит, что с расстояния 30 800 000 000 000 км Сириус сиял бы нам звездой 1,3-й величины, а паше Солнце 4,8-й величины, т. е. слабее Сириуса в
2,53,8 2,53,5 25 раз,
2,50,3
хотя видимый блеск Солнца в 10 000 000 000 раз больше блеска Сириуса.
Мы убедились, что Солнце – далеко не самая яркая звезда неба. Не следует, однако, считать наше Солнце совсем пигмеем среди окружающих его звёзд: светимость его всё же выше средней. По данным звёздной статистики, средними по светимости из звёзд, окружающих Солнце до расстояния 10 парсеков, являются звёзды девятой абсолютной величины. Так как абсолютная величина Солнца равна 4,8, то оно ярче, нежели средняя из «соседних» звёзд, в
|
2,58 |
2,54,2 |
50 раз. |
|
|
2,53,8 |
|||
Будучи в 25 раз абсолютно тусклее Сириуса, Солнце оказывается всё же в 50 раз ярче, чем средние из окружающих его звёзд.
Самая яркая звезда из известных
Самой большой светимостью обладает недоступная простому глазу звёздочка восьмой величины в созвездии Золотой Рыбы, обозначаемая
1) Вычисление можно выполнить по следующей формуле, происхождение которой станет ясно читателю, когда немного позднее он познакомится ближе с «парсеком» и «параллаксом»:
|
M |
2,5 |
m |
2 |
|
|
2,5 |
. |
|||
|
0,1 |
||||
Здесь М – абсолютная величина звезды, m – её видимая величина, π – параллакс звезды в
секундах. Последовательные преобразования таковы: 2,5M = 2,5m · 100π2,
M lg 2,5 = m lg 2,5 + 2 + 2 lg π, 0,4M = 0,4m +2 + 2 lg π,
откуда
M = m + 5 + 5 lg π.
Для Сириуса, например, m = –1,6π = 0″,38. Поэтому его абсолютная величина
M = –l,6 + 5 + 5 lg 0,38 = 1,3.
122
латинской буквой S. Созвездие Золотой Рыбы находится в южном полушарии неба и не видно в умеренном поясе нашего полушария. Упомянутая звёздочка входит в состав соседней с нами звёздной системы – Малого Магелланова Облака, расстояние которого от нас оценивается примерно в 12 000 раз больше, чем расстояние до Сириуса. На таком огромном удалении звезда должна обладать совершенно исключительной светимостью, чтобы казаться даже восьмой величины. Сириус, заброшенный так же глубоко в пространстве, сиял бы звездой 17-й величины, т. е. был бы едва виден в самый могущественный телескоп.
Какова же светимость этой замечательной звезды? Расчёт даёт такой результат: минус восьмая величина. Это значит, что наша звезда абсолютно в: 400 000 раз (примерно) ярче Солнца! При такой исключительной яркости звезда эта, будучи помещена на расстоянии Сириуса, казалась бы на девять величин ярче его, т. е. имела бы примерно яркость Луны в фазе четверти! Звезда, которая с расстояния Сириуса могла бы заливать Землю таким ярким светом, имеет бесспорное право считаться самой яркой из известных нам звёзд.
Звёздная величина планет на земном и чужом небе
Возвратимся теперь к мысленному путешествию на другие планеты (проделанному нами в разделе «Чужие небеса») и оценим более точно блеск сияющих там светил. Прежде всего укажем звёздные величины планет в максимуме их блеска на земном небе. Вот табличка.
На небе Земли:
|
Венера……………………….. |
–4,3 |
Сатурн………………………… |
–0,4 |
|
Марс……………………………. |
–2,8 |
Уран……………………………. |
+5,7 |
|
Юпитер……………………… |
–2,5 |
Нептун……………………….. |
+7,6 |
|
Меркурий…………………. |
–1,2 |
Просматривая её, видим, что Венера ярче Юпитера почти на две звёздные величины, т. е. в 2,52 = 6,25 раза, а Сириуса в 2,5-2,7 = 13 раз
(блеск Сириуса – 1,6-й величины). Из той же таблички видно, что тусклая планета Сатурн всё же ярче всех неподвижных звёзд, кроме Сириуса и Канопуса. Здесь мы находим объяснение тому факту, что планеты (Венера, Юпитер) бывают иногда днём видны простым глазом, звёзды же при дневном свете совершенно недоступны невооружённому зрению.
Далее приводим таблички блеска светил на небе Венеры, Марса и Юпитера без новых пояснений, так как они представляют собой лишь количественное выражение того, о чём говорилось уже в разделе «Чужие небеса»:
На небе Марса:
|
Солнце…………………… |
–26 |
|
Фобос ……………………. |
–8 |
|
Демос …………………… |
–3,7 |
|
Меркурий………………. |
–0,8 |
|
Венера…………………… |
–3,2 |
|
Юпитер………………….. |
–2,8 |
|
Земля…………………….. |
–2,6 |
|
Сатурн…………………… |
–0,6 |
123
Соседние файлы в папке Для школьников и студентов (Я.И. Перельман)
- #
- #
- #
- #
- #
- #
- #
27.10.20175.06 Mб65Perelman – Zanimatelnaya mekhanika 1951.djvu
- #
Светимость Солнца
- Светимость Солнца
-
Солнечная светимость,
— единица светимости, обычно используемая астрономами для представления светимости звёзд. Равна светимости Солнца, составляющей 3,827 × 1026 Вт или 3,827 × 1033 Эрг/с.
Расчёт константы
Вы можете рассчитать количество солнечной энергии, попадающей на Землю, путём сравнения площади сферы с радиусом, равным расстоянию Земли от Солнца (центр находится в звезде) и площади сечения, сделанного таким образом, чтобы ось вращения планеты принадлежала плоскости сечения.
- Радиус Земли — 6.378 км.
- Площадь сечения Земли: SЗемля = π×радиус² = 128.000.000 км²
- Среднее расстояние до Солнца: RСолнце = 150.000.000 км. (1 а.е.)
- Площадь сферы: SСолнце = 4×π×RСолнце² = 2,82×1017 км².
- Количество энергии в единицу времени, попадающей на Землю: PЗемля = PСолнце × SЗемля/SСолнце = 1,77×1017 Вт.
- Количество энергии (в единицу времени)на квадратный метр: PЗемля/SЗемля = 1387 Вт/м² (Солнечная постоянная)
- Человечество примерно потребляет 12×1012 Вт. Какая площадь необходима для обеспечения энергопотребления? Лучшие солнечные батареи имеют КПД около 33 %. Необходимая площадь составляет 12×1012/(1387×0,33) = 26×109 м² = 26000 км², или квадрат ~160×160 км. (На самом деле требуется бо́льшая площадь, так как солнце не всегда находится в зените и, к тому же, некоторая часть излучения рассеивается облаками и атмосферой.)
Ссылки
- I.-J. Sackmann, A. I. Boothroyd (2003). “Our Sun. V. A Bright Young Sun Consistent with Helioseismology and Warm Temperatures on Ancient Earth and Mars”. The Astrophysical Journal 583 (2): 1024-1039.
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое “Светимость Солнца” в других словарях:
-
Светимость — в астрономии полная энергия, излучаемая источником в единицу времени (в абсолютных единицах или в единицах светимости Солнца; светимость Солнца = 3,86·1033 эрг/с). Иногда говорят не о полной С., а о С. в некотором диапазоне длин волн. Напр., в… … Астрономический словарь
-
Светимость — Светимость термин, используемый для именования некоторых физических величин. Содержание 1 Фотометрическая светимость 2 Cветимость небесного тела … Википедия
-
Светимость звезды — Светимость звезды, сила света звезды, т. е. величина излучаемого звездой светового потока, заключённого в единичном телесном угле. Термин «светимость звезды» не соответствует термину «светимость» общей фотометрии. С. звезды может относиться как к … Большая советская энциклопедия
-
СВЕТИМОСТЬ — в точке поверхности. одна из световых величин, отношение светового потока, исходящего от элемента поверхности, к площади этого элемента. Единица С. (СИ) люмен с квадратного метра (лм/м2). Аналогичная величина в системе энергетич. величин наз.… … Физическая энциклопедия
-
СВЕТИМОСТЬ — СВЕТИМОСТЬ, абсолютная яркость ЗВЕЗДЫ количество энергии, излучаемой ее поверхностью в секунду. Выражается в ваттах (джоулях в секунду) или в единицах измерения яркости Солнца. Болометрическая светимость измеряет общую мощность света звезды на… … Научно-технический энциклопедический словарь
-
СВЕТИМОСТЬ — СВЕТИМОСТЬ, 1) в астрономии полное количество энергии, испускаемое космическим объектом в единицу времени. Иногда говорят о светимости в некотором диапазоне длин волн, например радиосветимость. Обычно измеряется в эрг/с, Вт или в единицах… … Современная энциклопедия
-
СВЕТИМОСТЬ — звезды мощность излучения. Обычно выражается в единицах, равных светимости Солнца L? = 3,86?1026 Вт … Большой Энциклопедический словарь
-
СВЕТИМОСТЬ (в астрономии) — СВЕТИМОСТЬ звезды, мощность излучения. Обычно выражается в единицах, равных светимости Солнца L¤ = 3,86Ч1026 Вт … Энциклопедический словарь
-
Светимость — I Светимость в точке поверхности, отношение светового потока (См. Световой поток), исходящего от малого элемента поверхности, который содержит данную точку, к площади этого элемента. Одна из световых величин (См. Световые величины).… … Большая советская энциклопедия
-
Светимость (в физике) — В общей физике, светимость плотность потока световой энергии в данном направлении. В экспериментальной физике элементарных частиц светимостью называют параметр ускорителя или коллайдера, характеризующий интенсивность столкновения встречных пучков … Википедия
Со́лнечная свети́мость, 
Расчёт константы[править | править код]
Светимость Солнца можно вычислить путём измерения количества энергии, попадающей в единицу времени на единичную площадку, находящуюся в окрестностях Земли (на расстоянии 1 а.e. от Солнца) и повёрнутую перпендикулярно к направлению падения солнечных лучей. Этот поток энергии называется солнечной постоянной, он равен в среднем A = 1361 Вт/м² (вариации связаны в основном с периодическими изменениями солнечной активности, они составляют около 0,1 %). Площадь сферы с радиусом R = 1 а.e. = 149 597 870 691 м равна S = 4πR2 ≈ 2,8123⋅1023 м2; следовательно, эту сферу пересекает поток энергии, равный AS = 3,827⋅1026 Вт.
Другой метод вычисления солнечной светимости основан на том факте, что Солнце с большой степенью точности представляет собой абсолютно чёрное тело. В результате количество энергии, излучаемой в секунду с единицы площади поверхности Солнца, зависит только от его температуры T, согласно закону Стефана — Больцмана: L⊙ = σT4×S☉, где σ — постоянная Стефана — Больцмана, S☉ = 4πR⊙2 — площадь поверхности Солнца.
См. также[править | править код]
- Солнечная масса
- Солнечный радиус
- Парадокс слабого молодого Солнца
Ссылки[править | править код]
- I.-J. Sackmann, A. I. Boothroyd. Our Sun. V. A Bright Young Sun Consistent with Helioseismology and Warm Temperatures on Ancient Earth and Mars (англ.) // The Astrophysical Journal : journal. — IOP Publishing, 2003. — Vol. 583, no. 2. — P. 1024—1039.
Эта заметка — о приёмах оценки, приближенных расчетов интересных величин. Применительно к Солнцу.
Средняя плотность тела — это масса тела, деленная на его объем. Если плотность постоянна, одинакова во всех точках, то средняя ей равна. Если нет, то можно сказать только одно: в какой-то точке плотность равна средней (но только при условии непрерывного распределения плотности).
Средняя плотность черной дыры на удивление быстро убывает с ростом радиуса горизонта событий. Под средней плотностью черной дыры мы подразумеваем среднюю плотность области, ограниченной горизонтом событий. Радиус горизонта пропорционален массе: мы это много раз обсуждали и совсем просто это можно получить из анализа размерностей. В самом деле, метр пропорционален секунде, так как скорость света постоянна. Гравитационная постоянная тоже постоянна, а ее размерность м³/(кг∙с²). Иными словами, килограмм пропорционален м³/с², а с учетом пропорциональности метра и секунды, килограмм пропорционален метру. Так что радиус может быть только пропорционален массе, никак иначе. Другое дело, что коэффициент пропорциональности очень мал.
Так вот, объем шара растет как куб радиуса, а масса внутри шара растет как радиус, так что средняя плотность убывает обратно пропорционально квадрату радиуса. Дыра вдвое большей массы имеет вчетверо меньшую среднюю плотность.
Но эту плотность ни к чему не пристегнуть.
Давайте вернемся к Солнцу. Нам дана его масса, 2∙10³⁰ кг, и расстояние до него: 1.5∙10¹¹м. Больше ничего не дано, кроме самого Солнца. Масса Солнца, кстати, почти точно в триста тысяч раз больше массы Земли, а 300000 — это скорость света в км/ч (никакой связи тут нет, чисто мнемоника!)
Диск Солнца можно покрыть большим пальцем на расстоянии вытянутой руки. То есть диск Солнца виден под тем же углом, что большой палец (порядка 1см) с расстояния вытянутой руки (порядка 1м). Иными словами, диаметр Солнца относится к расстоянию до него так же, как 1см к 1м. Или в сто раз меньше. То есть,1.5∙10⁹м.
Проверим: 1.4 млн км. Почти точно.
Объем шара считается по формуле (1⅓)πR³. Приближенно это 4R³: нам хватит такой точности. Радиус есть половина диаметра, но можно сразу через диаметр переписать формулу: D³/2. Получим 3.375∙10²⁷/2=1.67∙10²⁷м³. Делим массу Солнца на его объем: получается 1.2∙10³кг/м³=1.2г/см³. Плотность воды составляет 1000кг/м³=1г/см³. Получается, что плотность Солнца лишь чуть больше плотности воды и близка к глицерину: у него 1.261. Точное значение 1.4.
Внутри Солнце весьма плотное, зато поверхностные слои очень малой плотности: газ, милорды, газ.
Мы могли бы обойтись без массы Солнца, точнее, могли бы вычислить ее сами. Расстояние до Солнца A=1.5∙10¹¹м, значит, длина орбиты (она почти точно окружность) около 9∙10¹¹м. Земля пролетает такой путь за год, а в году немного более, чем 3∙10⁷с. Значит, скорость Земли составляет v=3∙10⁴м/с. И скорость эта — первая космическая для Солнца и для данного расстояния до его центра (или до самого Солнца, ошибка невелика).
Квадрат первой космической скорости равен GM/A, где G — гравитационная постоянная. Стало быть, 9∙10⁸м²/с²=GM/A, или GM=13.5∙10¹⁹. Гравитационная постоянная известна: это 6.67∙10⁻¹¹ в системе Си (метры-секунды-килограммы, размерность приведена выше). Делим и приблизительно получаем M=2∙10³⁰кг.
Давайте оценим мощность Солнца. Мы знаем, что на Землю поступает 1400 Ватт на квадратный метр: это солнечная постоянная. Но столько энергии поступает в секунду на любой квадратный метр на сфере радиусом А. Ее площадь равна 4πA², то есть 28∙10²²м². Умножая, получаем почти 4∙10²⁶Вт. Точный ответ 3.6-3.8, а не 4: неплохо.
Поделим на площадь Солнца. Его диаметр мы нашли, это D=1.5∙10⁹м, а формула площади сферы через диаметр вообще простая: πD². Так что площадь поверхности Солнца составляет примерно 7∙10¹⁸м². Поделим мощность Солнца на его площадь: получим примерно 5∙10⁷Вт/м².
Итак, Солнце излучает 50 мегаватт с квадратного метра. Точный ответ — 63 мегаватта. Если учесть, что Солнце — абсолютно чёрное тело, то можно воспользоваться законом Стефана-Больцмана. Поделив на их константу 5.6∙10⁻⁸Вт/м²/К⁴, получим четвертую степень температуры Солнца: 9∙10¹⁴. Извлекая корень четвертой степени (или квадратный дважды), получим примерно 5400К. Точное значение 5800К.
Теперь давайте прикинем энергоэффективность Солнца, поделив его мощность (4∙10²⁶Вт) на его массу (2∙10³⁰кг): получим 2∙10⁻⁴Вт/кг. Это до смешного мало, так как человек излучает намного больше. В самом деле, температура кожи 33 градуса, в одежде еще меньше (пусть 300К), так что чистое излучение порядка 450Вт с квадратного метра. Площадь кожи около 2 кв.м, что дает 900Вт без учета поглощения излучения извне. Делим на массу порядка 100кг и имеем 9Вт/кг.
Учтем поглощение при температуре в 20 градусов (293К). Получается около 400Вт/кв.м. То есть эффективно человек излучает примерно 100Вт, или около 1Вт/кг. Всё равно в пять тысяч раз эффективнее солнышка!
Правда, мы излучаем только инфракрасный свет, а солнышко — еще приятный видимый и ультрафиолетовый. И оно светит исправно миллиарды лет, а мы — без воздуха, воды, пищи и солнечного света — существенно меньше. Да и с этими всеми благами вопрос открытый. А если это всё учесть, то эффективность сразу снизится. В этом плане у звёзд конкурентов нет.
Давайте попробуем еще немного снизить зависимость от данных. Пока мы зависим только от расстояния от Земли до Солнца, которое измерить напрямую не можем. Зато мы можем измерить период обращения Венеры вокруг Солнца: он в полтора раза меньше нашего года, 224 дня, или около 2∙10⁷с. Положимся на закон Кеплера: квадраты периодов относятся как кубы расстояний до Солнца. Если годы Венеры и Земли относятся как ⅔, то в квадрате это 4/9; извлекаем кубический корень и получаем примерно 0.77. Так относятся расстояния до Солнца, то есть мы знаем отношение. Расстояние от Земли до Венеры в момент соединения (наиближайшего положения) измерено Котельниковым: 40 млн км, или 4∙10¹⁰м. Это разность расстояний от планет до Солнца.
Имеем два уравнения: x-y=4∙10¹⁰, y/x=0.77. Отсюда получаем 0.23х=4∙10¹⁰ и, окончательно, расстояние от Земли до Солнца х=1.7∙10¹¹м (неплохо, у нас было 1.5).
Можно использовать не год Венеры, а минимальное и максимальное расстояния (если максимальное 260 млн км нам тоже известно). Тогда x-y=4∙10¹⁰, x+y=26∙10¹⁰, откуда сразу x=15∙10¹⁰м.
Кто-то может возразить: мы заменили одно неизвестное на другое неизвестное. Верно, но так и работает наука. Мы не знаем этого и не можем измерить, но мы можем измерить что-то другое и вычислить желаемое…так и живем.
Давайте в заключение посчитаем, насколько бы хватило топлива, будь Солнце чисто химическим источником тепла и света. Мощность 4∙10²⁶Вт, масса 2∙10³⁰кг. Теплота горения водорода превышает 100МДж/кг, или 10⁸Дж/кг. Игнорируем кислород (понимаю) и получаем 2∙10³⁸Дж. На самом деле, конечно, в разы меньше, так как кислород намного тяжелее водорода, а его нужно лишь вдвое меньше. Ну пусть пока так. Делим этот запас энергии на расход (ватт — это джоуль в секунду): 5∙10¹¹с. В году, как я уже говорил, примерно 3∙10⁷с, то есть получаем 20000 лет, а на самом деле ещё меньше.
Если взять природный газ или нефть, то будет еще вдвое меньше; если уголь, то вчетверо; если дрова, то в 10, а то и более.
Любопытная шкала энергоэффективности! Для урана эффективность порядка 80ТДж/кг, или 8∙10¹³Дж/кг. В миллион раз (почти) эффективнее и, соответственно, в восемьсот тысяч раз дольше. Урановое Солнце могло бы светить миллиарды лет, прямо как термоядерное… каковым оно и является.
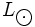 — единица светимости, обычно используемая астрономами для представления светимости звёзд. Равна светимости Солнца, составляющей 3,827 × 1026 Вт или 3,827 × 1033 Эрг/с.
— единица светимости, обычно используемая астрономами для представления светимости звёзд. Равна светимости Солнца, составляющей 3,827 × 1026 Вт или 3,827 × 1033 Эрг/с.