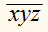Skip to content
Задача «Число десятков»
Условие
Дано натуральное число. Найдите число десятков в его десятичной записи.
Решение задачи от разработчиков на Python:
Другие интересные реализации задачи:
Смотреть видео — Задача «Число десятков» решение на Python
Делитесь с друзьями ссылкой на ответ и задавайте вопросы в комментариях! 👇
Related Posts
Формулировка задачи:
Разбор:
Чтобы найти число десятков числа n надо найти остаток от деления n на 100, а потом этоже чило делить нацело на 10.
Условие:
Дано натуральное число. Найдите число десятков в его десятичной записи (то есть вторую справа цифру его десятичной записи).
Код к задаче: «Число десятков»
textual
var a,n:integer; begin readln(n); a:=(n mod 100) div 10; writeln(a); end.
Полезно ли:
13 голосов , оценка 3.538 из 5
|
Есть 500 рублей. Потратили 200, осталось 300. Потратили 150, осталось 150. Потратили 90, осталось 60. Потратили 60, осталось 0. Если сложить оставшиеся части, получим 300 + 150 + 60 = 510. Откуда появились лишние 10 рублей? Почему сумма оставшихся денег равна 510 рублей? В интернете пишут, что только 7% людей могут решить эту задачу. Помнится в школе, мы на уроках (вроде бы алгебры) искали и находили какие-то доказательства любопытным методом, который назывался “от обратного”. Есть предложение и здесь перевернуть всё с ног на голову. То есть сначала прокрутить картинку на 180 градусов: А затем произвести вычисления в обратном порядке. Если в условии вычитались числа 200, 150, 90 и 60, то мы их тоже вычтем, но с другой стороны очереди, как показано стрелками. Что же мы получим в итоге? Давайте сведём наши расчёты в одну таблицу: Как видно, сумма промежуточных остатков чуть ли не вдвое превышает количество денег в кошельке до начала вычитаний. Мало того, если увеличить количество итераций до десяти-двадцати или вовсе каждый раз вычитать по рублю, то в нижней ячейке правого столбика можно будет получить сумму в десятки или даже в сотни раз превышающую число 500. О чём это говорит? Исключительно о том, что создатель вопроса искусно подобрал числовые значения так, чтобы два значения 500 и 510 незначительно отличались друг от друга и тем самым ввести нас в заблуждение. Ведь складывать следует только значения из второй колонки – то есть суммы денег, которые поэтапно изымались из нашего кошелька. Берём четыре значения из приведённой выше таблички и складываем. Что получилось? Пишем 60+90+150+200 = те самые 500 рубликов и никак не иначе. P.S. Кстати, обратите внимание, если из числа пятьсот сделать всего лишь одно вычитание, отняв ту самую пятисотку, то в результате в правой колоночке сразу нарисуется ноль. А путём подбора количества вычитаний и значений вычитаемых чисел можно получить и результаты в интервале от 1 до 499. Желающие могут поэкспериментировать. автор вопроса выбрал этот ответ лучшим Каролина 2 года назад Решение у этой загадки банальное, а объяснение одно – сумма остатков по правилам математики и не должна совпадать с суммой потраченных денег. Например, если из первоначальной суммы вычитать более мелкими “деньгами”, скажем, по 1 рублю, сумма остатков вообще может “зашкалить”. Считают только расход, либо приход, а если суммировать остатки – получится двойной учет, ведь часть денег, которые не были потрачены с первого раза, частично попадает в повторное сложение в каждом последующем остатке. Анжелика 13 2 года назад Вообще-то положено складывать не остатки а потраченные деньги. 200 + 150 + 90 + 60 – 500 Если складывать остатки то никак не выйдет нужная сумма. Это типа старой советской загадки про 50 рублей, которая до сих пор жива. Никольский 2 года назад Как тайное сделать явным? Просто. Какие у нас возникли траты? Постепенно тратились следующие суммы: 200, 150, 90 и 60 рублей. Введем обозначения: а=200, в=150, с=90 и d=60. Теперь поэтапно посмотрим, что будет происходить с тратами и остатками в буквенном выражении. Потратили а=200, осталось: в+с+d=300. Потратили в=150, осталось: с+d=150. Потратили с=90, осталось: d=60. Потратили d=60, осталось: 0. Стало быть потратили следующую сумму: а+в+с+d. А вот в остатках получили (в+с+d)+(с+d)+d — один раз в, два раза с, три раза d и ни одного раза а, что составило сумму в+2с+3d. Очевидно, что эти суммы не всегда равны. Именно что не всегда! Например, если с + 2d = а, то сумма потраченных денег будет таки равна сумме остатков. Пример: пусть с1=100, d1=50 тогда 200+150+100+50 = 300+150+50+0, где слева – сумма потраченных денег, а справа – сумма остатков. Поэтому в математике вы не найдете правила, которое каким бы то ни было образом урегулировало бы отношение между суммой потраченных денег и суммой остатков. Этот вопрос математика обходит молчанием. Да и что тут скажешь, когда то так, то эдак; то равны, то не равны. Ира ЛДВО на БВ 2 года назад Сумма оставшихся денег, как бы заумно загадка не звучала, и какие бы числа в рублях не наводили тень на плетень, равна нулю. Выходит последующий любой лукавый подсчёт не верен. Верен только тот который дан в вопросе в ту или иную сторону. В вопросе деньги отнимаются. А в ответе к нулю прибавляются: 60, 90, 150 и 200 и пятисотка виртуально в кармане, кошельке, руке. Это словно фильм пустить в обратном направлении. Про 7% вообще не понятно, даже среди неграмотного населения 100% на этот подвох не поймаешь, люди копейки считают, а тут рубли. Резюме: хорошая загадка улыбнуться, но не почувствовать себя в тех пресловутых 7%. Елена Шамсиева 2 года назад В заблуждение вводит то, что разница получилась совсем небольшой, и все начинают пересчитывать. Но тут изначально не верные числа взяты были – зачем складывать оставшиеся после каждой траты части? Нужно складывать то, что было потрачено. А это, конечно же, не одно и то же. Ведь каждый последующий остаток уже включает то, что оставалось в предыдущий раз. Для того чтобы лучше было понять, о чем я говорю, представьте не бумажные деньги и сдачу с них, а рублёвые монетки. На предпоследнем шаге осталось 60 монеток,но их же уже считали на предыдущих шагах. Cappuccino 2 года назад Это вранье, что только 7% могут решить эту задачу. Так специально пишут, чтобы вы почувствовали себя умным, который входит в 7% людей. Складывается совсем не то, что надо – вот и ответ неверный. Таких глупых задач в интернете полно. Georstargiystar 2 года назад Смотри 500-200 = 300 300 – 150 = 150 150 – 90 = 60 60 – 60 = 0 500+300+150+60= 1010 200+ 150+90+60 = 500 1010 – 500 = 510 Надеюсь понятно объяснил) А на счет 7% сомневаюсь мне кажется больше 70% увидели подвох Евгений трохов 2 года назад Надо складывать потраченные суммы, а не оставшиеся. Пример: Было 10 рублей, потратили 9 рублей – остался 1 рубль. Далее потратили этот последний 1 рубль- осталось 0 рублей. Сложим потраченные суммы: 9+1=10 рублей . Сложим остатки: 1+0=1-это никоим образом не 10 рублей. Все понятно. А в данной задаче про 500 рублей специально такие числа подобраны чтобы запутать читающего. нужно складывать сколько ты потратил, а не сколько осталось, чтобы получилась сумма 500рэ. Предположим если оставшиеся 60 рэ разбить еще на несколько. Например из оставшихся 60 р потратили 30р, осталось 30р. из оставшихся 30р потратили 10р. осталось 20р итд… и сумма остатков будет больше 500 рублей. SerKar246 2 года назад Сумма остатков не должна равняться сумме. Например вы потратили 1 рубль, потом еще 1 и еще 1. Это не значит, что 499 + 498 + 497 = 500. Так что это просто неверное высказывание. Но числа подобраны так, чтобы это не было сразу очевидно. ДарьяОлеговна3103 2 года назад Так потратили 200+150+90+60,как раз 500 и получается. Странная загадка какая-то Знаете ответ? |

Здравствуйте.
На этот вопрос меня сподвигла задача из питонтьютора:
“Дано натуральное число. Найдите число десятков в его десятичной записи.”
“Классическое математическое” решение этой задачи:
| Python | ||
|
“Гуманитарное” решение основывается на том, что десятки это всегда вторая цифра с конца числа (от 0 до 9):
| Python | ||
|
Код работает, если числа больше 9. Если меньше: IndexError на строке 1: string index out of range.
Как вписать в код условие “если n меньше 9, то n=0” для положительных чисел от 0 до 9 и для отрицательных от -1 до -9?
Спасибо.
Обозначение
десятеричной записи числа.
Запись
обозначает число, в
котором х сотен, у десятков и z единиц. Это число можно представить в виде
многочлена:
где
х – цифра указывающая
количество сотен в числе
у – цифра указывающая количество
десятков в числе
z – цифра указывающая
количество единиц в числе.
ПРИМЕР:
Четырёхзначное число с цифрами a, b, c
и d можно обозначить
Эта запись означает
1000a + 100b + 10c + d.
ПРИМЕР:
378
= 100 × 3 + 10 × 7 + 8.
ЗАДАЧА:
В двузначном числе цифра десятков на 4 больше цифры единиц. Когда это число
разделили на цифру единиц, то в частном получилось 24, а в остатке число, которое
на 2 меньше делителя. Найти задуманное число.
РЕШЕНИЕ:
Решая эту
задачу, можно использовать обозначение десятеричной записи числа. Заданное
число можно обозначить
В
соответствии с этим обозначением можно записать:
а по условию задачи имеем:
= 24
и ост (х – 4) – 2
=
24(х – 4) + х – 6.
10х + х
– 4 = 24(х – 4) + х – 6,
10х – 4 = 24х – 96 – 6,
14х
= 98, х = 7, тогда 10 × 7 + 7 – 4 = 73.
Задуманное число 73.
Алгоритм
решения задач, в которых используется формула двузначного числа.
Вводится
обозначение:
х – цифра десятков
у – цифра единиц
Искомое
двузначное число
10х + у
Составляется
система уравнений.
ЗАДАЧА:
Двузначное число в четыре раза больше суммы
его цифр. Если к этому числу прибавить произведение его цифр, то получится 32. Найдите это
двузначное число.
РЕШЕНИЕ:
х – цифра
десятков, у – цифра
единиц.
10х + у – искомое число, тогда по условию задачи:
2х2 + 12х – 32 = 0,
х2 + 6х
– 16 = 0.
х1 = –8 (посторонний корень)
х1 = 2, тогда у =
4.
ОТВЕТ: 24
Задания к уроку 37