54
1.
Задача 1
“Исследование
напряженно-деформированного состояния
в
точке тела”
Цель решения этой
задачи – усвоение основ теории напряжений
и деформаций.
Полагаем, что
напряженно-деформированное состояние
тела было
определено расчетами или экспериментально.
1.1.
Напряженное состояние в точке
тела
Мысленно
вырежем в окрестности произвольной
точки
![]()
нагруженного тела элементарный
(бесконечно малый) параллелепипед, грани
которого перпендикулярны координатным
осям
![]() .
.
Условие
задачи.
Компоненты напряжений, действующие по
граням параллелепипеда, равны
следующим величинам:

(1.1)
Э

Рис. 1
ти компоненты напряженного состояния
показаны на рис. 1 с учетом
правила знаков, принятого в теории
упругости (см. первую часть учебного
пособия, стр. 6).
Совокупность
нормальных и касательных напряжений
на трех взаимно перпендикулярных
площадках

называют тензором
напряжений.
Напряженное
состояние (НС) в точке полностью
определено, если известны шесть
компонентов тензора напряжений
![]()
(см. рис. 1), т. е., зная эти шесть компонентов
напряжений в
точке, можно вычислить напряжения на
любой
площадке, проходящий через
эту точку.
Найдем напряжения
на некоторой наклонной к осям
![]()
площадке, проходящей через заданную
точку. Положение площадки относительно
осей координат определяется направляющими
косинусами
![]()
внешней нормали
![]()
к этой площадке. Вначале вычисляем
значения проекций на оси координат
![]()
полного напряжения
![]()
по формулам:

(1.2)
Затем находим
величину полного напряжения:
![]()
(1.3)
Зная проекции
![]() ,
,
полного напряжения, действующего по
наклонной площадке, можно определить
нормальное
![]()
и касательное
![]()
напряжения по формулам:
![]()
![]()
(1.4)
![]()
![]()
(1.5)
Р

Рис.
2
ассмотрим применение формул
(1.2)-(1.5), используя исходные данные (1.1).
Пусть положение
внешней нормали к площадке
![]()
(рис. 2) относительно координатных осей
![]()
определено следующими значениями
направляющих косинусов (табл. 1.2 первой
части учебного пособия):
![]()
![]()
![]()
Полезно проверить
правильность величин направляющих
косинусов
подстановкой
их в выражение
![]()
(1.6)
которое должно
превращаться в тождество.
Подставляя значения
напряжений и направляющих косинусов в
формулы (1.3), получим:

(1.7)
С

Рис. 3
оставляющие полного напряжения и,
имеющие знак минус, противоположны
направлениям осей
![]()
и
![]() .
.
Положительная составляющая
![]()
направлена вдоль положительной оси y
(см. рис.2).
Значения
![]() ,
,
![]()
и
![]() ,
,
вычисленные по формулам (1.3)–(1.5) с учетом
заданных напряжений (1.1) и направляющих
косинусов, имеют следующие значения:
![]()
![]()
Напряжение
![]()
имеет знак плюс. Следовательно, оно
будет направлено от сечения (рис. 3).
1.1.2. Вычисление проекции касательного напряжения на заданное направление
Направление
касательного напряжения
![]()
в плоскости
сечения с внешней нормалью
![]()
относительно
любых
двух ортогональных осей
![]()
и
![]() ,
,
лежащих в той же плоскости определяется
следующим образом.
Вначале
определяются проекции полного напряжения
![]()
на оси
![]()
и
![]()
в виде
![]()
и
![]()
(рис. 4).
З
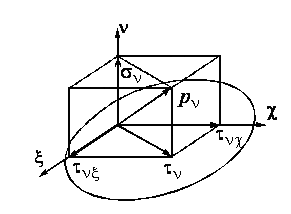
Рис. 4
атем угол
![]()
между касательным напряжением
![]()
и, например, осью
![]()
найдем по формуле
![]()
Напомним,
как найти, например,
![]()
– проекцию
полного напряжения
![]()
на ось
![]() .
.
Обозначим
направляющие косинусы
оси
![]() ,
,
как
![]() ,
,
и спроектируем
![]()
на ось
![]() :
:
![]()
(1.8)
Подставляя в (1.8)
вместо
![]()
их значения
в виде
(1.2), получим
![]()
![]()
![]()
(1.9)
Здесь
![]()
– направляющие косинусы внешней нормали
![]()
к площадке, по которой действует
касательное напряжение
![]() .
.
Рассмотрим вновь
трехгранную призму, показанную на рис.
3. Найдём проекцию касательного напряжения
![]() ,
,
действующую по площадке ВСК,
на ось
![]() ,
,
т.е. касательное напряжение
![]()
(см. рис. 3).
Внешняя нормаль
к площадке ВСК
совпадает с положительной осью
![]()
и её направляющие косинусы
![]()
(1.10)
Направляющие
косинусы оси
![]()
имеют следующие значения:
![]()
(1.11)
Вычислим касательное
напряжение
![]()
по формуле (1.9) с учётом (1.1), (1.10) и (1.11):
![]()
Поскольку внешняя
нормаль к площадке совпадает с
положительной осью
![]() ,
,
то отрицательное касательное напряжение
![]()
будет направлено в сторону, противоположную
направлению оси
![]()
(см. рис. 3).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Эпюры касательных напряжений для прямоугольного, двутаврового, круглого сечений
Эпюры касательных напряжений прямоугольного сечения
При выводе формулы Журавского предполагалось: балка имеет прямоугольное поперечное сечение (рис. 7.11), поэтому
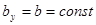 ;
;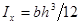 ;
;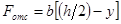 ;
; 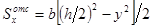
где y – расстояние от точки, в которой определяется касательное напряжение, до нейтральной оси x.
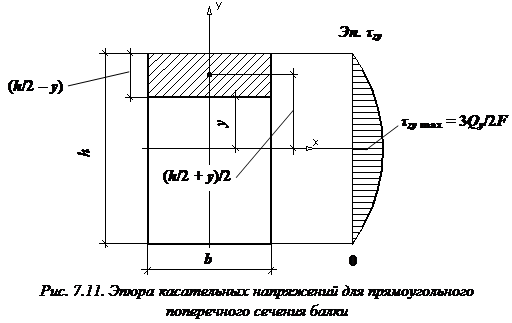 Подставляя эти формулы в формулу Журавского, для касательных напряжений получим:
Подставляя эти формулы в формулу Журавского, для касательных напряжений получим:
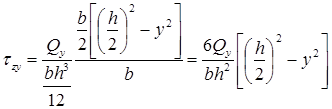
Касательные напряжения изменяются по высоте поперечного сечения по закону квадратичной параболы (см. рис. 7.11).
При 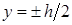 (для наиболее удаленных от нейтральной оси точек)
(для наиболее удаленных от нейтральной оси точек) 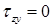 .
.
Для точек, расположенных на нейтральной оси (при 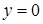 ),
), 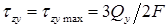 .
.
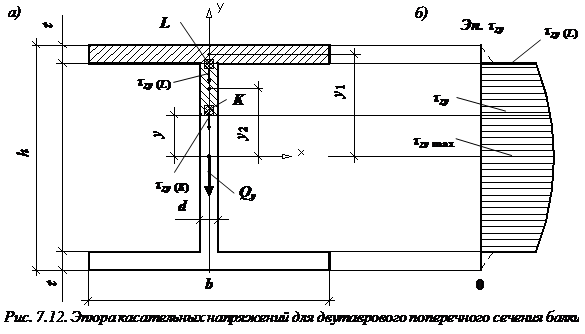
Эпюры касательных напряжений двутаврового сечения
Характерная особенность двутаврового сечения: резкое изменение ширины поперечного сечения (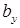 ), где полка соединяется со стенкой.
), где полка соединяется со стенкой.
Определим касательное напряжение в некоторой точке K (рис. 7.12), проведя через нее сечение, ширина которого равна толщине стенки: 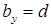 .
.
Рассмотрим верхнюю отсеченную часть поперечного сечения (заштрихована на рис. 7.12), статический момент инерции которой относительно нейтральной оси x равен сумме статических моментов инерции полки и заштрихованной части стенки:
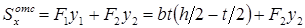
Эпюра касательных напряжений для двутаврового сечения представлена на рис. 7.12, б.
Касательные напряжения 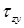 , возникающие в точках полки двутавра, по формуле Журавского вычислять нельзя, поскольку при ее выводе использовалось допущение о равномерности распределения касательных напряжений по ширине поперечного сечения, что справедливо только если ширина сечения
, возникающие в точках полки двутавра, по формуле Журавского вычислять нельзя, поскольку при ее выводе использовалось допущение о равномерности распределения касательных напряжений по ширине поперечного сечения, что справедливо только если ширина сечения 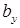 невелика. Однако очевидно, что касательные напряжения малы и не оказывают практического влияния на прочность балки. Эпюра касательных напряжений для двутаврового сечения показана штриховой линией (см. рис. 7.12, б).
невелика. Однако очевидно, что касательные напряжения малы и не оказывают практического влияния на прочность балки. Эпюра касательных напряжений для двутаврового сечения показана штриховой линией (см. рис. 7.12, б).
Формула касательного напряжения в точке L ( где полка соединяется со стенкой):
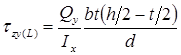
Наибольшие касательные напряжения возникают в точках, лежащих на нейтральной оси x.
Эпюры касательных напряжений круглого сечения
Для построения эпюры касательных напряжений круглого сечения выясним направление касательных напряжений при изгибе, возникающих в некоторой точке контура поперечного сечения стержня.
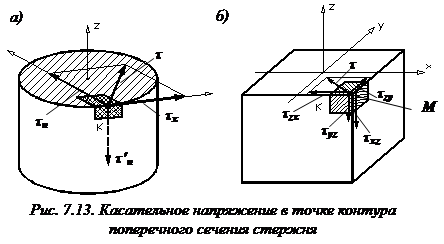 Рассмотрим произвольное поперечное сечение стержня (рис. 7.13, а).
Рассмотрим произвольное поперечное сечение стержня (рис. 7.13, а).
Предположим: в некоторой точке контура К касательное напряжение при изгибе 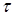 направлено произвольно по отношению к контуру. Разложим касательное напряжение на две составляющие
направлено произвольно по отношению к контуру. Разложим касательное напряжение на две составляющие 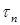 и
и 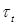 , направленные соответственно по нормали и касательной к контуру. Если касательное напряжение
, направленные соответственно по нормали и касательной к контуру. Если касательное напряжение 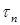 существует, то по закону парности касательных напряжений на поверхности стержня должно существовать равное ему по значению касательное напряжение при изгибе
существует, то по закону парности касательных напряжений на поверхности стержня должно существовать равное ему по значению касательное напряжение при изгибе 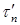 . Поскольку поверхность стержня свободна от внешних сил, параллельных оси балки z, касательное напряжение на поверхности стержня
. Поскольку поверхность стержня свободна от внешних сил, параллельных оси балки z, касательное напряжение на поверхности стержня 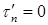 и, следовательно,
и, следовательно, 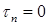 .
.
Таким образом, в точке контура поперечного сечения, поверхность которого не нагружена продольными внешними нагрузками, касательное напряжение при изгибе направлено по касательной к контуру.
Покажем, что в вершине угла поперечного сечения стержня касательное напряжение равно нулю (рис. 7.13, б).
Предположим, что в вершине угла (в точке M) возникает касательное напряжение 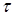 . Разложим его на составляющие касательные напряжения
. Разложим его на составляющие касательные напряжения 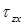 и
и 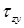 . По закону парности касательных напряжений эти составляющие равны нулю, поскольку равны нулю напряжения на поверхности стержня
. По закону парности касательных напряжений эти составляющие равны нулю, поскольку равны нулю напряжения на поверхности стержня 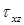 и
и 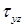 .
.
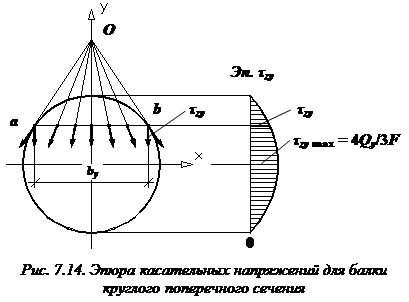 |
Задача вычисления касательных напряжений в произвольной точке балки круглого поперечного сечения усложняется. Однако если сделать предположение: в точках, расположенных на некоторой линии ab (рис. 7.14), касательные напряжения 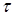 при изгибе направлены так, что все они пересекаются в точке О, и вертикальные проекции этих напряжений равномерно распределены вдоль линии ab, то формулу Журавского можно использовать для вычисления вертикальных проекций
при изгибе направлены так, что все они пересекаются в точке О, и вертикальные проекции этих напряжений равномерно распределены вдоль линии ab, то формулу Журавского можно использовать для вычисления вертикальных проекций 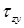 при построении эпюр касательных напряжений стержня круглого сечения. Вычисление остальных величин, входящих в формулу Журавского, производится, как и для прямоугольного поперечного сечения.
при построении эпюр касательных напряжений стержня круглого сечения. Вычисление остальных величин, входящих в формулу Журавского, производится, как и для прямоугольного поперечного сечения.
Наибольшие касательные напряжения, возникающие в точках, расположенных на нейтральной оси x, вычисляются по формуле:
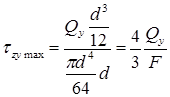
Пример решения задачи на теорию напряженного состояния.
Дано : σx=50 МПа; σy=60 МПа; τxy=70 МПа; E=1.3*105 МПа; μ=0.22
Требуется:
1. Определить величину главных напряжений и положение главных площадок;
2. Найти максимальные касательные напряжения τmax;
3. Определить относительные деформации и относительное изменение объёма;
4. Установить удельную потенциальную энергию деформации.
Решение.
1. Определим величину главных напряжений и положение главных площадок
В соответствии с правилом знаков, устанавливаем : σx=50 МПа ; σy=60 МПа ; τyx=-τxy
По формуле
σmax/min=![]() определим величину главных напряжений.
определим величину главных напряжений.
σmax=![]() =125,2 МПа
=125,2 МПа
σmin=![]() = – 15,2 МПа
= – 15,2 МПа
Для определения положения главных площадок используем формулу:
tg2α0=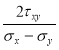 =
=![]() = 14 = tg86°
= 14 = tg86°
откуда 2α0=86° и α0=43°
Для определения площадки, по которой действуют напряжения σmax , поворачиваем горизонтальную площадку (так как по ней действуют нормальные напряжения, больше, чем по вертикальной площадке) на угол α0=43° против часовой стрелки, т.е. в том направлении, в котором вектор касательного напряжения (на поворачиваемой площадке) стремиться вращать элементарный параллелепипед относительно его центра. Найденная площадка показана на рисунке.
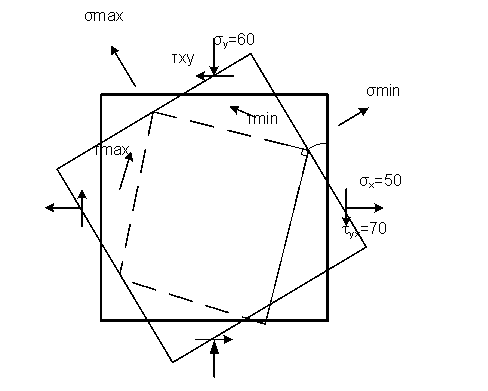
2. Найдём максимальные касательные напряжения τmax
Максимальные касательные напряжения находим по формуле :
τmax/min=![]() =
=![]() =±140,4 МПа
=±140,4 МПа
Положения площадок сдвига (по которым касательные напряжения имеют максимальные значения) определяем по положениям главных площадок, к которым они наклонены под углами 45°. Экстремальные касательные напряжения действуют в направлениях от σmin к σmax.
3. Определим относительные деформации и относительное изменение объёма
Относительные деформации находим по формулам:
εx=(1/E)[σx–μσy]=1/(1.3*1011)[50-0.22*60]*106=2,83*10-4
εy=(1/E)[σy–μσx]=1/(1.3*1011)[60-0.22*50]*106=3,77*10-4
Относительное изменение объёма по формуле Ж
θ=εx+εy=(2,83+3,77)*10-4=6,6*10-4
4. Установим удельную потенциальную энергию деформации.
Удельную потенциальную энергию деформации находим по формуле:
u=![]() = =
= =![]() =57956,7 Дж/м3
=57956,7 Дж/м3
Ответ : σmax=125,2 МПа; σmin= -15,2 МПа; τmax/min=±140,4 МПа; εx=2,83*10-4 ; εy=3,77*10-4 ; θ=6,6*10-4 ; u=57956,7 Дж/м3.
Определение касательных напряжений в двутавровом сечении. Рассмотрим сечение двутавра. Sx=96,9 см3; Yх=2030 см4; Q=200 кН

Для определения касательного напряжения применяется формула Д.И. Журавского![]() ,где Q — поперечная сила в сечении, Sx0 – статический момент части поперечного сечения, расположенной по одну сторону от слоя, в котором определяются касательные напряжения, Ix – момент инерции всего поперечного сечения, b – ширина сечения в том месте, где определяется касательное напряжение
,где Q — поперечная сила в сечении, Sx0 – статический момент части поперечного сечения, расположенной по одну сторону от слоя, в котором определяются касательные напряжения, Ix – момент инерции всего поперечного сечения, b – ширина сечения в том месте, где определяется касательное напряжение
Вычислим максимальное касательное напряжение:
Вычислим статический момент для верхней полки:
![]()
Теперь вычислим касательные напряжения:
Строим эпюру касательных напряжений:

Касательные напряжения в балке двутаврового сечения
Содержание:
- Напряжения в поперечных сечениях
- Касательные напряжения
- Пример решения задачи 1.
- Пример решения задачи 2
- Расчет на прочность
- Пример решения задачи 3
- Пример решения задачи 4
В инженерной практике часто применяются балки с поперечным сечением, имеющим вертикальную ось симметрии. Если внешняя нагрузка и реактивные усилия лежат в одной плоскости, которая совпадает с осью симметрии сечения, то балка будет изгибаться в той же плоскости. Такой изгиб называется плоским (рис.1). 
При плоском поперечном изгибе в сечениях балки возникают два внутренних усилия – поперечная сила  и изгибающий момент
и изгибающий момент  (рис.2).
(рис.2). 
Напряжения в поперечных сечениях
Поскольку поперечная сила  является равнодействующей касательных напряжений
является равнодействующей касательных напряжений  (рис.3), а изгибающий момент
(рис.3), а изгибающий момент  – равнодействующей нормальных напряжений
– равнодействующей нормальных напряжений  (рис.4), то, следовательно, в поперечных сечениях балки в общем случае возникают и нормальные напряжения
(рис.4), то, следовательно, в поперечных сечениях балки в общем случае возникают и нормальные напряжения  и касательные
и касательные 

Можно показать, что нормальные напряжения  распределяются по высоте сечения по линейному закону (рис.5). Линия, во всех точках которой
распределяются по высоте сечения по линейному закону (рис.5). Линия, во всех точках которой  называется нейтральной линией. В рассматриваемом случае плоского вертикального изгиба нейтральная линия совпадает с осью
называется нейтральной линией. В рассматриваемом случае плоского вертикального изгиба нейтральная линия совпадает с осью 
По мере удаления от нее напряжения возрастают по модулю, достигая наибольших по модулю значений в крайних точках сечения, наиболее удаленных от нейтральной линии.

Чтобы определить нормальные напряжения в произвольной точке  используется следующая формула
используется следующая формула

где  – величина изгибающего момента в рассматриваемом сечении, определяется по эпюре
– величина изгибающего момента в рассматриваемом сечении, определяется по эпюре 
 – осевой момент инерции поперечного сечения, табличная величина;
– осевой момент инерции поперечного сечения, табличная величина;
 – координата точки, в которой определяется напряжение.
– координата точки, в которой определяется напряжение.
Возможно вам будут полезны данные страницы:
Знак  определяется с помощью эпюры
определяется с помощью эпюры  Подробнее это будет рассмотрено при решении конкретных задач.
Подробнее это будет рассмотрено при решении конкретных задач.
Преобразуя формулу (1), можно получить формулу для определения максимальных напряжений 

где  – осевой момент сопротивления сечения, табличная величина.
– осевой момент сопротивления сечения, табличная величина.
Касательные напряжения
Касательные напряжения  в поперечном сечении балки определяются по формуле Журавского:
в поперечном сечении балки определяются по формуле Журавского:

где  – величина поперечной силы в рассматриваемом сечении, определяется по эпюре
– величина поперечной силы в рассматриваемом сечении, определяется по эпюре 
 – осевой момент инерции всего сечения, табличная величина;
– осевой момент инерции всего сечения, табличная величина;
 – статический момент отсеченной части сечения, определяется по формуле:
– статический момент отсеченной части сечения, определяется по формуле:
 – координата отсеченной части сечения;
– координата отсеченной части сечения;
 ее площадь;
ее площадь;  – ширина сечения на уровне отсеченной части. Распределение касательных напряжений по высоте поперечного сечения зависит от формы самого сечения. На рис.6 приведены эпюры касательных напряжений для некоторых часто встречающихся форм поперечных сечений балки.
– ширина сечения на уровне отсеченной части. Распределение касательных напряжений по высоте поперечного сечения зависит от формы самого сечения. На рис.6 приведены эпюры касательных напряжений для некоторых часто встречающихся форм поперечных сечений балки.

Как видно из этих рисунков, максимальной величины касательные напряжения достигают на нейтральной линии, а в крайних точках сечения они равны нулю. Рассмотрим примеры определения нормальных и касательных напряжений.
Пример решения задачи 1.
1) Пусть в опасном сечении балки, сечение которой изображено на рис.7, возникают изгибающий момент  растягивающий нижние волокна и
растягивающий нижние волокна и  Определить нормальные и касательные напряжения в точке
Определить нормальные и касательные напряжения в точке  а также наибольшие нормальные и касательные напряжения. Построить эпюру распределения нормальных напряжений по высоте сечения.
а также наибольшие нормальные и касательные напряжения. Построить эпюру распределения нормальных напряжений по высоте сечения.  Решение:
Решение:
1) Покажем на чертеже сечения положение центра тяжести  и проводим оси
и проводим оси  Это будет система главных центральных осей, так как ось
Это будет система главных центральных осей, так как ось  совпадает с осью симметрии сечения.
совпадает с осью симметрии сечения.
2) Выпишем из справочника [3, табл.5] формулу для определения момента инерции  для треугольного сечения и подставим численные значения
для треугольного сечения и подставим численные значения 
3) Найдем нормальные напряжения в точке  используя формулу (1)
используя формулу (1)

Эти напряжения будут отрицательными, так как согласно условию задачи растягиваются нижние волокна сечения, то есть выше нейтральной линии (ось  лежит зона сжатия, а ниже – зона растяжения. Точка
лежит зона сжатия, а ниже – зона растяжения. Точка  находится в зоне сжатия, поэтому
находится в зоне сжатия, поэтому 
4) Найдем наибольшее нормальное напряжение. Поскольку сечение несимметрично относительно оси  то целесообразно пользоваться формулой (1). Из чертежа видно, что наибольшие сжимающие напряжения возникают в точке 1, так как эта точка является наиболее удаленной от нейтральной линии в зоне сжатия. Наибольшие растягивающие напряжения возникают в нижних точках сечения
то целесообразно пользоваться формулой (1). Из чертежа видно, что наибольшие сжимающие напряжения возникают в точке 1, так как эта точка является наиболее удаленной от нейтральной линии в зоне сжатия. Наибольшие растягивающие напряжения возникают в нижних точках сечения 
По полученным данным построим эпюру  (рис.7).
(рис.7).
5) Найдем касательное напряжение в точке  Сначала проведем через точку
Сначала проведем через точку  линию, параллельную оси
линию, параллельную оси  и назовем отсеченной часть сечения, лежащую выше этой линии. Обозначим через точку
и назовем отсеченной часть сечения, лежащую выше этой линии. Обозначим через точку  центр тяжести отсеченной части и вычислим его координату
центр тяжести отсеченной части и вычислим его координату  Из чертежа видно
Из чертежа видно

статический момент отсеченной части.
Используем формулу (3):

Здесь  ширина основания отсеченной части.
ширина основания отсеченной части.
Пример решения задачи 2
Пусть в сечении балки возникают поперечная сила  и изгибающий момент
и изгибающий момент  растягивающий верхние волокна. Определить наибольшие нормальные и касательные напряжения.
растягивающий верхние волокна. Определить наибольшие нормальные и касательные напряжения. 
Решение:
1) Покажем положение главной центральной системы координат 
2) Найдем осевой момент сопротивления  используя справочник
используя справочник 

3) Так как сечение симметрично относительно оси  и удобнее использовать формулу (2).
и удобнее использовать формулу (2).

Согласно условию задачи растягиваются верхние волокна, поэтому 

4) Из рис.6 следует, что наибольшие касательные напряжения возникают в точках, лежащих на нейтральной линии, поэтому проводим линию, совпадающую с осью  Отсеченной будет, например, верхняя часть сечения, т.
Отсеченной будет, например, верхняя часть сечения, т.  -центр тяжести этой части, т.е. полукруга.
-центр тяжести этой части, т.е. полукруга.
Найдем  используя формулу из [3, табл.5]:
используя формулу из [3, табл.5]:

Найдем момент инерции всего сечения (т.е. круга) [3, табл.5]:

Используем формулу (3)

Построим эпюры  (рис.8).
(рис.8).
Расчет на прочность
Расчет на прочность начинается с построения эпюр внутренних усилий балки  Сечение, в котором величина
Сечение, в котором величина  достигает наибольшего значения, считается опасным сечением. Именно для такого сечения и делается расчет на прочность.
достигает наибольшего значения, считается опасным сечением. Именно для такого сечения и делается расчет на прочность.
Если балка выполнена из пластического материала, который одинаково работает на растяжение и сжатие, то условие прочности записывается в виде:

где  – расчетное сопротивление, заданная величина .
– расчетное сопротивление, заданная величина .
Если балка выполнена из хрупкого материала, который неодинаково работает на растяжение и сжатие, то используются два условия прочности.

где  расчетное сопротивление на растяжение,
расчетное сопротивление на растяжение,
 расчетное сопротивление на сжатие.
расчетное сопротивление на сжатие.
Как правило, расчет балки на прочность производится только по нормальным напряжениям, так как в подавляющем большинстве балок величина нормальных напряжений намного превосходит величину напряжений касательных. Однако в следующих случаях проверяется и условие прочности по касательным напряжениям:
- 1) если рассчитываемая балка выполнена из дерева, так как дерево плохо сопротивляется скалыванию вдоль волокон;
- 2) если балка короткая;
- 3) если на балку действуют большие сосредоточенные силы, приложенные на наибольших расстояниях от опор.
В последних двух случаях поперечные сечения в балке достигают большой величины, в то время как изгибающие моменты за счет малых плеч сравнительно невелики.
Условие прочности по касательным напряжениям записывается в виде:

где  расчетное сопротивление на срез.
расчетное сопротивление на срез.
Пример решения задачи 3
Проверить выполнение условий прочности по нормальным и касательным напряжениям для деревянной балки (рис.9), если 

Решение:
1) Строим эпюры  Опасным является сечение в заделке,
Опасным является сечение в заделке,  (рис.9).
(рис.9).
2) Проверим условие прочности по нормальным напряжениям

Величина  была определена в примере 2:
была определена в примере 2:

Условие прочности по нормальным напряжениям выполняется.
3) Проверим условие прочности по касательным напряжениям

Величину  берем из примера 2:
берем из примера 2:

Условие прочности по касательным напряжениям выполняется. Замечание.
Во всех последующих примерах будем использовать только условие прочности по нормальным напряжениям.
Пример решения задачи 4
Проверить выполнение условия прочности для балки, выполненной из чугуна, если 

Решение: 1) Построим эпюры внутренних усилий  Опасным является сечение в заделке
Опасным является сечение в заделке  (рис.10). 2) Так как балка выполнена из хрупкого материала, то проверяем два условия прочности (5):
(рис.10). 2) Так как балка выполнена из хрупкого материала, то проверяем два условия прочности (5):

Значения напряжений  были определены в примере 1.
были определены в примере 1.

Условие прочности на сжатие выполняется.

Условие прочности на растяжение не выполняется.
