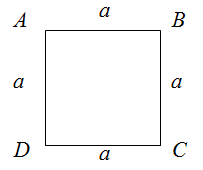Квадрат — это геометрическая фигура, правильный четырехугольник, у которого все углы и стороны равны.
Онлайн-калькулятор периметра квадрата
Противоположные стороны квадрата параллельны.
Другими словами, квадрат — это прямоугольник, у которого все стороны равны, или квадрат — это ромб, у которого все углы прямые. Квадрат имеет две диагонали, которые делятся точкой их пересечения пополам. Диагонали квадрата также делят его углы пополам и соединяют несмежные вершины.
Формула периметра квадрата
Для того чтобы найти периметр квадрата, нужно сложить длины всех его сторон.
P=a+a+a+a=4⋅aP=a+a+a+a=4cdot a
aa — длина стороны квадрата.
Разберем задачу на нахождение периметра квадрата.
Найти периметр квадрата со стороной 12 см.
Решение
a=12a=12
Воспользуемся формулой нахождения периметра квадрата и подставим вместо aa его численное значение:
P=4⋅a=4⋅12=48P=4cdot a=4cdot 12=48 см.
Ответ: 48 см.
Ищете, где заказать решение контрольной работы? Эксперты Студворк с радостью помогут вам!
Тест по теме «Периметр квадрата»
Памятка
для решения задач, нахождение периметра фигур
1. Задача
Найди
периметр треугольника со сторонами 3см, 5см, 6см.
Объясняю:
Чтобы найти периметр треугольника, нужно все 3 стороны сложить.
Запись в тетради:
Р
= 3 + 5 + 6 = 14 (см)
Ответ:
14 см периметр треугольника.
2. Задача
Найди
периметр прямоугольника со сторонами 2см и 5см.
Объясняю:
1
способ: Чтобы найти периметр прямоугольника,
нужно все 4 стороны сложить.
Запись в тетради:
Р
= 2 + 5 + 2 + 5 = 14 (см) или Р = 2 + 2 + 5 + 5 = 14 (см)
Ответ:
14 см периметр прямоугольника.
2
способ: Чтобы найти периметр прямоугольника
применю формулу Р = (а + b)·2,
где а – длина одной стороны, b
– длина второй стороны.
В
формулу вместо букв поставлю известные данные Р = (2 + 5)·2
= 14 (см)
Запись в тетради:
Р
= (2 + 5)·2 = 14 (см)
Ответ:
14 см периметр прямоугольника.
3. Задача
Найди
периметр квадрата со стороной 3 см.
Объясняю:
1 способ:
Чтобы найти периметр квадрата, нужно все 4 стороны сложить
Запись в тетради:
Р = 3 + 3 + 3 + 3 = 12
(см)
Ответ: 12 см периметр
квадрата.
2 способ: Чтобы
найти периметр квадрата применю формулу Р = а·4,
где а – длина стороны квадрата. В формулу вместо буквы а,
поставлю известные данные
Запись в тетради:
Р = 3·4
= 12 (см)
Ответ: 12 см периметр
квадрата.
4. Задача
Длина одной
из сторон прямоугольника равна 6 см, длина другой стороны – на 4 см больше.
Найди периметр прямоугольника.
Объясняю:
У прямоугольника противоположные стороны равны. Чтобы найти периметр прямоугольника,
нужно все 4 стороны сложить. Но неизвестна вторая сторона, найду сначала её. В
задаче сказано, что она больше первой на 4см, буду прибавлять: 1) 6 + 4 = 10
(см) – вторая сторона. Все стороны известны, могу найти периметр, сложу все
четыре стороны: 2) 6 + 6 + 10 + 10 = 32 (см)
Запись в тетради:
1) 6
+ 4 = 10 (см) – вторая сторона.
2) 6
+ 6 + 10 + 10 = 32 (см) или Р = (6 + 10)·2 = 16·2
= 32 (см)
Ответ: 32 см периметр
прямоугольника.
5. Задача
Длина одной
из сторон прямоугольника равна 8 см, длина другой стороны – на 5 см меньше.
Найди периметр прямоугольника.
Объясняю:
У прямоугольника противоположные стороны равны. Чтобы найти периметр прямоугольника,
нужно все 4 стороны сложить. Но неизвестна вторая сторона, найду сначала её. В
задаче сказано, что она меньше первой на 5 см, буду вычитать: 1) 8 – 5 = 3
(см) – вторая сторона. Все стороны известны, могу найти периметр, сложу все
четыре стороны: 2) 8 + 8 + 3 + 3 = 22 (см)
Запись в тетради:
1) 8
– 5 = 3 (см) – вторая сторона.
2) 8
+ 8 + 3 + 3 = 22 (см) или Р = (8 + 3)·2 = 11·2
= 22 (см)
Ответ: 22 см периметр
прямоугольника.
6. Задача
Начерти
квадрат, периметр которого равен 16 см.
Объясняю: Чтобы начертить
квадрат, нужно знать длину стороны, а она неизвестна. Я знаю, что у квадрата
все четыре стороны равны, что периметр квадрата равен 16 см. Разделю периметр
16 см на 4 стороны, получу одну сторону.
Запись в тетради:
16 : 4 = 4 (см) – сторона
квадрата
Черчу квадрат
 |
В данной публикации мы рассмотрим, каким образом можно посчитать периметр квадрата и разберем примеры решения задач.
-
Формула вычисления периметра
- По длине стороны
- По длине диагонали
-
Примеры задач
Формула вычисления периметра
По длине стороны
Периметр (P) квадрата равняется сумме длин его сторон.
P = a + a + a + a
Так как все стороны квадрата равны, формулу можно представить в виде произведения:
P = 4 ⋅ a
По длине диагонали
Периметр (P) квадрата равен произведению длины его диагонали на число 2√2:
P = d ⋅ 2√2
Данная формула следует из соотношения длин стороны (a) и диагонали (d) квадрата:
d = a√2.
Примеры задач
Задание 1
Найдите периметр квадрата, если его сторона равна 6 см.
Решение:
Используем формулу, в которой участвует значение стороны:
P = 6 см + 6 см + 6 см + 6 см = 4 ⋅ 6 см = 24 см.
Задание 2
Найдите периметр квадрата, диагональ которого равняется √2 см.
Решение 1:
С учетом известной нам величины воспользуемся второй формулой:
P = √2 см ⋅ 2√2 = 4 см.
Решение 2:
Выразим длину стороны через диагональ:
a = d / √2 = √2 см / √2 = 1 см.
Теперь, используя первую формулу, получаем:
P = 4 ⋅ 1 см = 4 см.
Содержание:
- Формула
- Примеры вычисления периметра квадрата
Формула
Чтобы найти периметр квадрата, необходимо длину его стороны умножить на четыре.
По определению, квадрат – это правильный четырехугольник, у которого все углы и стороны равны. Тогда, если задан квадрат
$ABCD$ со стороной
$a$, то для него формула для нахождения периметра примет вид:
$$P_{Delta A B C D}=a+a+a+a=4 a$$
Примеры вычисления периметра квадрата
Пример
Задание. Дан квадрат
$ABCD$ со стороной
$a=0,25$ см. Вычислить периметр заданного квадрата.
Решение. Для нахождения периметра квадрата воспользуемся формулой
$$P_{Delta A B C D}=4a$$
Подставляя в неё значение 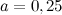
$P_{Delta A B C D}=4 cdot 0,25=1$ (см)
Ответ. $P_{Delta A B C D}=1$ (см)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
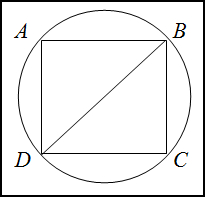
Задание. Найти периметр квадрата
$ABCD$, который вписан в окружность радиуса
$r=2$ дм.
Решение. Сделаем рисунок.
Диаметр описанной окружности является диагональю вписанного в неё квадрата, то есть
$DB=d=2r=2 cdot 2=4$ (дм)
Известно, что сторона квадрата $AB$ связана с его диагональю
$DB$ соотношением:
$$D B=A B sqrt{2}$$
Откуда получаем, что
$A B=frac{D B}{sqrt{2}}=frac{4}{sqrt{2}}=2 sqrt{2}$ (дм)
А тогда искомый периметр:
Ответ. $P_{Delta A B C D}=8 sqrt{2}$ (дм)
Читать дальше: как найти периметр прямоугольника.

{P = 4 cdot a}
Периметр квадрата рассчитывается довольно просто, но если вы забыли формулу или не имеете под рукой калькулятора, мы собрали для вас формулы для расчета периметра квадрата и онлайн калькулятор, который рассчитает периметр по длине стороны, диаметру, радиусам вписанной или описанной окружности, площади.
Содержание:
- калькулятор периметра квадрата
- формула периметра квадрата через длину стороны
- формула периметра квадрата через диагональ
- формула периметра квадрата через площадь
- формула периметра квадрата через радиус описанной окружности
- формула периметра квадрата через радиус вписанной окружности
- примеры задач
Квадрат – четырехугольник, у которого все стороны равны и все углы равны (прямые, 90 градусов). Квадрат так же называют правильным четырехугольником. Квадрат является частным случаем прямоугольника и ромба.
Кроме квадрата на сайте вы можете найти периметр ромба, прямоугольника, параллелограмма.
Формула периметра квадрата через длину стороны
{P = 4 cdot a}
a – сторона квадрата
Формула периметра квадрата через диагональ
{P = 2 sqrt{2} cdot d}
d – диагональ квадрата
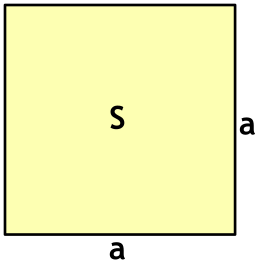
Формула периметра квадрата через площадь
{P = 4sqrt{S}}
S – площадь квадрата
Формула периметра квадрата через радиус описанной окружности
{P = 4sqrt{2} cdot R}
R – радиус описанной около квадрата окружности
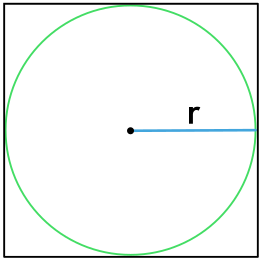
Формула периметра квадрата через радиус вписанной окружности
{P = 8r}
r – радиус вписанной в квадрат окружности
Примеры задач на нахождение периметра квадрата
Задача 1
Найти периметр квадрата, вписанного в окружность с R = 4√2.
Решение
Среди формул для решения этой задачи используем наиболее подходящую формулу №4. В условии сказано про квадрат, вписанный в окружность. Но при этом окружность будет описана около квадрата. Именно поэтому мы используем эту формулу. Подставим в нее известный из условия радиус вписанной окружности (в нашем случае он будет являться радиусом описанной окружности):
P = 4sqrt{2} cdot R = 4sqrt{2} cdot 4sqrt{2} = ({4sqrt{2}})^2 = {4^2 cdot ({sqrt{2}})^2} = 16 cdot 2 = 32 : см
Ответ: 32
Проверить полученный ответ можно с помощью калькулятора . Однако, радиус задан не просто числом, а выражением с квадратным корнем – 4√2. К счастью, наш калькулятор может анализировать математические выражения и производить с ними вычисления. Так как на клавиатуре компьютера нет знака квадратного корня, ввести значение радиуса необходимо в таком виде – 4*sqrt(2).
Задача 2
Найдите периметр квадрата сторона которого 13см.
Решение
Чтобы решить эту задачу используем первую формулу:
P = 4 cdot a = 4 cdot 13 = 52 : см
Ответ: 52 см
Проверить ответ поможет калькулятор .
Задача 3
Найдите периметр квадрата сторона которого 5см.
Решение
Для решения этой задачи также используем первую формулу:
P = 4 cdot a = 4 cdot 5 = 20 : см
Ответ: 20 см
Проверить ответ поможет калькулятор .
Задача 4
Найдите периметр квадрата с диагональю 2√2.
Решение
При решении этой задачи воспользуемся формулой №2:
P = 2 sqrt{2} cdot d = 2 sqrt{2} cdot 2 sqrt{2} = ({2 sqrt{2}})^2 = 2^2 cdot ({sqrt{2}})^2 = 4 cdot 2 = 8 : см
Ответ: 8 см
Проверить ответ к этой задаче можно с помощью калькулятора . Диагональ задана выражением с квадратным корнем, введем ее в виде, который сможет распознать наш калькулятор – 2 * sqrt(2).