Задача как найти расстояние между остановками

Он заметил, что ему все равно, к какой остановке идти. То есть, например, он идёт к 1 остановке, против движения автобуса. Допустим, что он приходит на остановку, и одновременно приезжает автобус, и он сразу садится. Если же он выйдет в это же время и пойдёт ко 2 остановке, по ходу движения, то этот же самый автобус его догонит, и опять он придёт на остановку одновременно с автобусом. Это и означает, что ему все равно, к какой остановке идти. А теперь внимание, вопрос: Если расстояние между остановками считать за 1, то на каком расстоянии от первой остановки стоит его дом? Рассмотреть разные случаи для разного соотношения скоростей человека и автобуса. В том числе случай, когда человек едет, например, на роликах, быстрее автобуса. бонус за лучший ответ (выдан): 20 кредитов Пусть человек доходит от дома до второй остановки за время t2, до первой – за время t1. Ровно столько же времени потребуется человеку чтобы дойти от первой остановки до дома. Таким образом, на путь от первой остановки до второй человеку требуется время (t2+t1). Автобус за время t1 подходит к первой остановке, за время t2 – ко второй. Значит от одной остановки до другой он проходит за время (t2-t1). Пусть скорость человека х, а скорость автобуса в k раз больше, т.е. k*x. Расстояние между остановками (t2+t1)*х=(t2-t1)*k*­x. Получаем уравнение: (t2+t1)=(t2-t1)*k (1). Тогда отношение расстояния от дома до первой остановки к расстоянию между остановками (обозначим его “а”) равно а=t1/(t2+t1). Выразив время t2 через t1 и k, и подставив его в выражение для а и проведя преобразования, получим очень простую формулу: а=0,5-0,5/k. График зависимости а от k (а – ордината, k – абсцисса), представляет собой гиперболу с асимптотами “отрицательное направление оси ординат” и прямой а=0,5. Из него сразу становится ясно, что k >= 1, и значения а лежат в пределах 0<=а<0,5. P/S. Задачу решил сразу же как ознакомился с условием, но буквально тут же попал “в бан”, а когда бан закончился, были уже представлены все решения, в том числе и авторское. Некоторое время размышлял, стоит ли представлять свой вариант, но решил всё-таки стоит, так как мой вариант проще и нагляднее всех других. автор вопроса выбрал этот ответ лучшим Mefod­y66 [35.1K] 5 лет назад  Напишу правильное решение. Обозначим скорости автобуса и пешехода va и vp. Пусть в момент выхода из дома расстояние автобуса от 1 остановки равно S, а от 2 остановки S+1. Расстояние от дома до 1 остановки x, до 2 остановки 1-x. Время, за которое пешеход дойдёт до 1 остановки, равно времени, за которое автобус доедет до этой же 1 остановки. t1 = S/va = x/vp Время, за которое автобус и пешеход дойдут до 2 остановки t2 = (S+1)/va = (1-x)/vp Составляем пропорции S*vp = x*va (S+1)*vp = (1-x)*va Раскрываем скобки S*vp = x*va S*vp + vp = va – x*va Подставляем 1 уравнение во 2 уравнение x*va + vp = va – x*va 2x*va = va – vp x = (va – vp)/(2*va) = 1/2 – vp/(2*va) Вот насколько дом левее середины отрезка между остановками. Если скорость va = vp, то x = 1/2 – 1/2 = 0 Дом должен находиться на 1 остановке. Если скорость пешехода в 2 раза меньше скорости автобуса, то x = 1/2 – 1/4 = 1/4 расстояния между остановками. Вариант, что человек движется быстрее автобуса (или с одинаковой с ним скоростью) можно выкинуть из рассмотрения вовсе – ибо в этом случае автобус его никогда не догонит, когда человек движется в сторону 2-й остановки. Остаётся вариант, что человек движется медленнее автобуса. Тогда ясно, что расстояние от его дома до 1-й остановки должно быть меньше половины единицы. Насколько меньше, зависит от соотношения его скорости и скорости автобуса. Скорость автобуса больше скорости человека в ((1-2х)/х), где х – расстояние до первой остановки. Например, если расстояние до 1-й остановки равно 0.1 (от той единицы, что составляет расстояние между остановками), то скорость автобуса больше в 4-ре раза. Если если расстояние до 1-й остановки равно 0.2, то скорость автобуса больше в 3-и раза. smog2­605 [14.6K] 5 лет назад  Довольно неожиданная задача. Примем обозначения. В таком случае несложно составить расчет выхода пешехода к первой и второй остановкам. А также введем коэффициенты скоростей и расстояний. Приравняем скорости t1 и t2. В результате преобразований почти все сократится и останется простенькое выражение, определяющее взаимосвязь между коэффициентами расстояний (k) и скоростей (p). Произведем замену. Получим такой график, который даст ответ на все поставленные вопросы. Соотношение скоростей не может быть больше 1. То есть, автобус всегда быстрее. В случае равенства скоростей (p=1), человек должен жить на первой остановке. Если он не сядет в автобус, то одновременно с ним достигнет второй остановки. Если p=0, то есть скорость пешехода равна нулю, то жилище должно находится на середине пути, поскольку все равно куда идти, а точнее НЕ идти. Пример: точка на графике. Если скорость человека в половину от скорости автобуса, то он должен жить на четверти пути от первой остановки. И напоследок маленькая игрушка. Предположим между остановками 1.5 километра. Скорость автобуса 30 км/ч, пешехода 5 км/ч. В таком случае он должен искать жилье на расстоянии 625 метров от первой остановки. ССЫЛКА НА МАКЕТ P.S. Выставил ответ и увидел ответ автора, который появился на пол часа раньше. Мне не хочется удалять свой ответ. Я на него потратил время и желание. Евген­ий трохо­в [56.3K] 5 лет назад  Пусть дом находится на расстоянии х от первой остановки.Тогда х+(1-х)=1.Пусть С -расстояние от автобуса до первой остановки,п- скорость автобуса,н-скорость человека,м- первое время( время движения автобуса и человека до первой остановки),т- второе время ( время движения автобуса и человека до второй остановки) Составим выражения С=мп. х=мн. С+1=тп. 1- х=тн.Решая их получим зависимость п/н=1/(1-2 х) .Получается что по условиям задачи должна быть вот такая связь между этими тремя величинами.Параметр х вообще- то лежит в пределах 0<х< 1 ,но значения х большие или равные 1/2 не имеют смысла( получается что отношение скоростей- отрицательная величина или бесконечная ).И ещё,в целом вся эта дробь больше единицы,поэтому в том случае если скорость человека превышает скорость автобуса тоже получается что дробь меньше единицы а значит (1-2 х)>1 ,отсюда 2х < 0, что противоречит условию.То есть нормальные варианты получаются только в том случае если человек живёт ближе к первому дому и скорость автобуса превышает скорость человека. Дом находится посредине между остановками, то есть 0,5 расстояния от дома до каждой из остановок. В таком случае неважна скорость и способ передвижения от дома до остановок. Время всегда будет равное и никакого выигрыша не будет в вариантах, то есть выходить можно в одно и то же время из дома, чтобы попасть на этот автобус. Выигрыш мог бы быть, если бы проезд оплачивался по километрам, а не так, как сейчас в городе платят все одинаково, независимо от длительности. Ну и выигрыш может быть тогда, когда автобус может не прибыть и придется далее идти пешком. Тогда лучше шагать до остановки, которая ближе к пункту назначения. Еще не рассматриваем случай, когда дорога идет под уклон, об этом ничего не говорится. Тогда легче идти к той остановке, к которой дорога идет вниз. Расстояние может быть больше, скорость выше, а время – одинаковое. То же самое с ветром, он может быть попутным или встречным. Но, по условию задачи, пешеходу все равно как идти, значит, дорога ровная, ветра нет, как и собак, хулиганов и т.п. Знаете ответ?

Как найти расстояние между остановками, если известно…? Подскажите пожалуйста

Автобусы специального городского маршрута, приезжая на конечную остановку, ожидают одну минуту, после чего едут в обратном направлении. Известно, что от конечной остановки автобусы отправляются каждые 10 минут. Ровно в тот момент, когда школьник подбежал к конечной остановке, двери автобуса закрылись, и он уехал. Мальчик решил пойти пешком до следующей остановки. Он шёл со скоростью 5 км/ч, и в середине пути между остановками мимо него проехал следующий автобус, следуя к конечной остановке. Увеличив скорость до 10 км/ч, школьник успел добежать до остановки и сел в этот автобус.
Найдите расстояние между остановками. Считайте, что все автобусы движутся с одинаковой постоянной скоростью. Ответ выразите в км, округлите до сотых.

---

Пусть расстояние между остановками x, тогда мальчик прошел полпути со скорость 5 км/ч и полпути со скоростью 10 км/ч. На всю дорогу у него ушло 10 минут между остановками и 1 минуту ожидания, так как по условию он успел добежать и сесть. Переведем время в часы 11 мин = 11/60 часов.
Составим уравнение:
(x/2)/5 + (x/2)/10 = 11/60
Помножим все коэффициенты на 60 и решим:
6*x + 3*x = 11
9*x = 11
x = 11/9 = 1,22
Мой ответ: расстояние между остановками 1,22 км.

Он заметил, что ему все равно, к какой остановке идти.

То есть, например, он идёт к 1 остановке, против движения автобуса. Допустим, что он приходит на остановку, и одновременно приезжает автобус, и он сразу садится.

Если же он выйдет в это же время и пойдёт ко 2 остановке, по ходу движения, то этот же самый автобус его догонит, и опять он придёт на остановку одновременно с автобусом.

Это и означает, что ему все равно, к какой остановке идти.

А теперь внимание, вопрос:

Если расстояние между остановками считать за 1, то на каком расстоянии от первой остановки стоит его дом?

Рассмотреть разные случаи для разного соотношения скоростей человека и автобуса.

В том числе случай, когда человек едет, например, на роликах, быстрее автобуса.

подробнее о бонусах

бонус за лучший ответ: 20 кредитов
хотите увеличить?

тэги:

движение,

задача,

математика

категория:

образование

ответить

в избранное

бонус

Vasil Stryzhak
[7.6K]

Когда на роликах быстрее автобуса, то зачем нужен он. Во-первых, быстрее добираться до места. Во-вторых, можно сэкономить время на утренней зарядке (больше поспать), а главное — выгодно. Но вот если проездной в кармане, то все кардинально меняется и верно.
— 16 часов назад

комментировать

3 ответа:

старые выше
новые выше
по рейтингу

1

Евген­ий трохо­в
[17.6K]

13 часов назад

Пусть дом находится на расстоянии х от первой остановки.Тогда х+(1-х)=1.Пусть С -расстояние от автобуса до первой остановки,п- скорость автобуса,н-скорость человека,м- первое время( время движения автобуса и человека до первой остановки),т- второе время ( время движения автобуса и человека до второй остановки) Составим выражения С=мп. х=мн. С+1=тп. 1- х=тн.Решая их получим зависимость п/н=1/(1-2 х) .Получается что по условиям задачи должна быть вот такая связь между этими тремя величинами.Параметр х вообще- то лежит в пределах 0<х< 1 ,но значения х большие или равные 1/2 не имеют смысла( получается что отношение скоростей- отрицательная величина или бесконечная ).И ещё,в целом вся эта дробь больше единицы,поэтому в том случае если скорость человека превышает скорость автобуса тоже получается что дробь меньше единицы а значит (1-2 х)>1 ,отсюда 2х < 0, что противоречит условию.То есть нормальные варианты получаются только в том случае если человек живёт ближе к первому дому и скорость автобуса превышает скорость человека.

комментировать

в избранное

ссылка

отблагодарить

1

msb
[97.5K]

13 часов назад

Дом находится посредине между остановками, то есть 0,5 расстояния от дома до каждой из остановок. В таком случае неважна скорость и способ передвижения от дома до остановок. Время всегда будет равное и никакого выигрыша не будет в вариантах, то есть выходить можно в одно и то же время из дома, чтобы попасть на этот автобус. Выигрыш мог бы быть, если бы проезд оплачивался по километрам, а не так, как сейчас в городе платят все одинаково, независимо от длительности. Ну и выигрыш может быть тогда, когда автобус может не прибыть и придется далее идти пешком. Тогда лучше шагать до остановки, которая ближе к пункту назначения. Еще не рассматриваем случай, когда дорога идет под уклон, об этом ничего не говорится. Тогда легче идти к той остановке, к которой дорога идет вниз. Расстояние может быть больше, скорость выше, а время — одинаковое. То же самое с ветром, он может быть попутным или встречным. Но, по условию задачи, пешеходу все равно как идти, значит, дорога ровная, ветра нет, как и собак, хулиганов и т.п.

комментировать

в избранное

ссылка

отблагодарить

1

Nasos
[16.4K]

16 часов назад

Вариант, что человек движется быстрее автобуса (или с одинаковой с ним скоростью) можно выкинуть из рассмотрения вовсе — ибо в этом случае автобус его никогда не догонит, когда человек движется в сторону 2-й остановки.

Остаётся вариант, что человек движется медленнее автобуса.

Тогда ясно, что расстояние от его дома до 1-й остановки должно быть меньше половины единицы.

Насколько меньше, зависит от соотношения его скорости и скорости автобуса.

Скорость автобуса больше скорости человека в ((1-2х)/х), где х — расстояние до первой остановки.

Например, если расстояние до 1-й остановки равно 0.1 (от той единицы, что составляет расстояние между остановками), то скорость автобуса больше в 4-ре раза.

Если если расстояние до 1-й остановки равно 0.2, то скорость автобуса больше в 3-и раза.

комментировать

в избранное

ссылка

отблагодарить

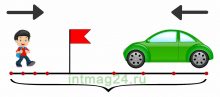Чтобы быстро решить задачи на движение, в том числе сложные и запутанные, нужно составить к ней схему или таблицу данных.

• Схемы задач на движение помогают представить наглядно условие задачи и найти верное решение.
• Таблица к задачам на движение позволяет структурировать данные, чтобы наглядно видеть исходные данные и неизвестные величины.

Поэтому, чтобы решить сложные задачи на движение, нужно нарисовать схему, а в дополнение к схеме рекомендуется нарисовать таблицу, где в шапке параметры скорости, времени и расстояния. При этом везде применяется основная формула:

Рассмотрим решение следующих типов задач:

• простые задачи на скорость, время и расстояние;
• задачи на движение в разных направлениях: сближение и удаление;
• задачи на движение в одном направлении: сближение и удаление;
• решение задач на движение по реке.

Решить простые задачи на движение

Для решения простых задач на движение, как правило, схема или таблица не требуется, в них применяется формула нахождения скорости, времени или расстояния. Но иногда, чтобы не запутаться в решении, лучше воспользоваться каким-либо методом. Рассмотрим схему и таблицу, чтобы вы смогли выбрать наиболее удобный для себя способ разобраться в задаче.

Задача 1. Средняя скорость

Первые 5 часов автомобиль ехал со скоростью 60 км/ч, следующие 3 часа — со скоростью 100 км/ч, а последние 4 часа — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

Решение.
Нарисуем схему движения.

Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)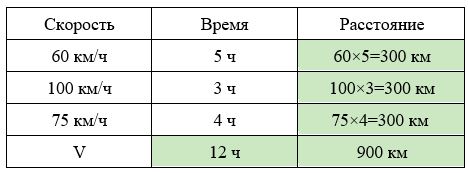 

Средняя скорость — это отношение пройденного пути ко времени, за который пройден этот путь.

• Найдем общее расстояние: 900 км.
• Найдем время в пути: 5 + 3 + 4 = 12 часов.
• Найдем среднюю скорость автомобиля: 900:12 = 75 км/ч.

Задача 2. Движение с остановкой

В 9:00 велосипедист выехал из пункта А в пункт Б. Доехав до пункта Б, он сделал остановку на полчаса, а в 11:30 выехал обратно с прежней скоростью. В 13:00 ему оставалось проехать 8 км до пункта А. Найдите расстояние между пунктами А и Б.

Решение.
Нарисуем схему движения.

Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности.

• Найдем скорость: 8 : 0,5 = 16 км/ч
• Найдем расстояние: 16×2=32 км.

Задача 3. Уровень ЕГЭ.

Лыжник планировал проехать 10 км с горы за 20 минут с постоянной скоростью v. Вместо этого первые несколько километров он проехал в два раза быстрее, чем планировал, а оставшиеся километры он проехал в два раза медленнее, чем планировал. В итоге весь путь занял у него 34 минуты. Сколько километров лыжник проехал в два раза быстрее, чем планировал?

Решение.
Нарисуем схему движения.

Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)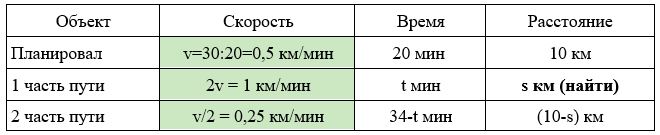

• Найдем скорость, с которой лыжник планировал скатиться: 10 : 20 = 0,5км/мин
• Найдем скорости, с которыми лыжник скатывался: 3км/мин и 0,25км/мин.
• Составим систему уравнений:
  1) 1×t=s  → t=s
  2) 0,25×(34-t)=10-s → 0,25×(34-s)=10-s → s=2 км.

Решить задачи на движение в разных направлениях: сближение и удаление

Задача 4. Скорость удаления

Два автомобиля выехали одновременно из одного и того же пункта в противоположных направлениях. Скорость первого автомобиля  100  км/ч, скорость второго —  70  км/ч. Какое расстояние будет между автомобилями через  4  часа?

Решение.
Нарисуем схему движения.

Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом) /

Способ 1.
1) 100× 4 = 400 (км)  — проехал первый автомобиль,
2) 70 × 4 = 280 (км)  — проехал второй автомобиль.
3) 400 + 280 = 680 (км).

Способ 2.
1)  (100 + 70),  170  км/ч — это скорость удаления автомобилей.
2) 170× 4 = 680 км.

Задача 5. Скорость сближения

Расстояние между городами А и В равно 750 км. Из города А в город В со скоростью 50 км/ч выехал первый автомобиль, а через три часа после этого навстречу ему из города В выехал со скоростью 70 км/ч второй автомобиль. На каком расстоянии от города А автомобили встретятся?

Решение.
Нарисуем схему движения.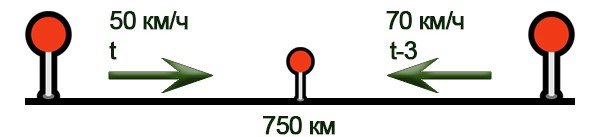

Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)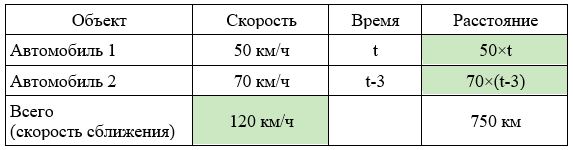

Способ 1.

• Составим уравнение: 50×t + 70×(t-3) =750
• Решим уравнение: 120t=960; t=8 часов.
• По условиям задачи нужно найти расстояние от пункта А, то есть расстояние для первого автомобиля: 50×8=400км.

Способ 2.

• За первые три часа пути автомобиль, выехавший из города А, проехал 150 километров и расстояние от него до города В стало равным 600 км.
• Скорость сближения двух автомобилей равна 120 км/ч, значит, они встретятся через 5 часов после выезда второго автомобиля: 600:120=5 часов.
• Таким образом, первый автомобиль всего ехал  8 часов: 50×8=400км.

Задача 6. Скорость сближения

Расстояние между пунктами А и В равно 135 км. Из пункта А в пункт В выехал легковой автомобиль. Одновременно с ним из пункта В в пункт А выехал грузовой автомобиль, скорость которого на 15 км/ч меньше скорости легкового. Через час после начала движения они встретились. Через сколько минут после встречи грузовой автомобиль прибыл в пункт А?

Решение.
Нарисуем схему движения.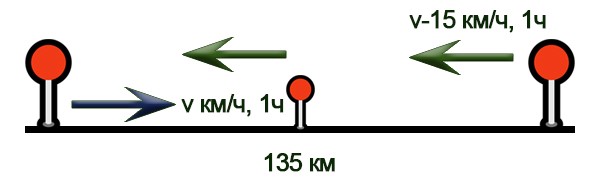

Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)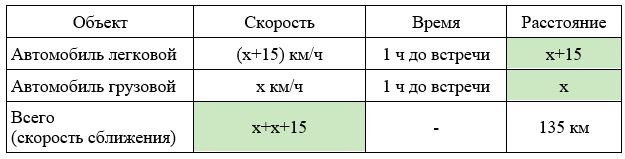

• Пусть x км/ч — скорость грузового автомобиля, тогда (x + 15) км/ч — скорость легкового автомобиля. Получаем уравнение: x+x+15=135; x=60км/ч. 
• Найдем сколько времени грузовой автомобиль затратил на весь путь: 135:60=2,25 часов.
• Найдем сколько времени грузовой автомобиль затратил на путь после встречи: 2,25-1=1,25 часов или 75 минут (1,25*60).
• Ответ: 75 мин.

Задача 7. Уровень ЕГЭ.

Два поезда движутся навстречу друг другу – один со скоростью 70 км/ч, другой со скоростью 80 км/ч. Пассажир, сидящий во втором поезде, заметим, что первый поезд прошел мимо него за 12 секунд. Какова длина первого поезда? Ответ дайте в метрах.

Решение.
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)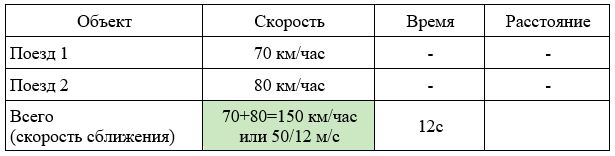

• Найдем скорость сближения: 70+80=150км/ч.
• Переведем ее в другие единицы измерения: 150 км/ч = 150000/3600 = 50/12 м/с
• Заметим, что фраза “первый поезд прошел мимо пассажира за 12с” означает, что с того момента, как пассажир увидел голову поезда, до того момента, как он увидел хвост поезда, прошло 12с.
  
• Найдем расстояние 50/12 × 12 =50 метров.

Решить задачи на движение в одном направлении: сближение и удаление

Задача 8. Скорость сближения

Поезд, двигаясь равномерно со скоростью 63 км/ч, проезжает мимо идущего в том же направлении параллельно путям со скоростью 3 км/ч пешехода за 57 секунд. Найдите длину поезда в метрах.

Решение.
Нарисуем схему движения.

Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)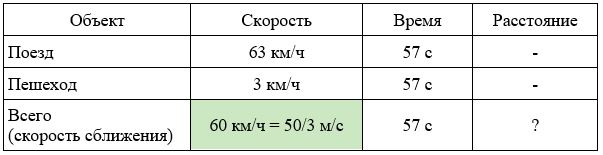

• Найдем скорость поезда относительно пешехода: 63 − 3 = 60 км/ч
• Переведем скорость сближения в другие единицы измерения: 60 км/ч = 60000/3600=50/3 м/с.
• Найдем длину поезда (расстояние, которое проехал поезд): (50/3)*57=950 м.

Задача 9. Скорость сближения

Два туриста одновременно вышли в одном направлении в город N. При этом вышли они из разных городов, расстояние между которыми 9 км. Известно, что турист, изначально находившийся дальше от города N, шёл со скоростью, в два раза превышающей скорость другого туриста. В город N они прибыли одновременно, через 3 часа после начала движения. Найдите скорость туриста, который шёл быстрее. Ответ дайте в км/ч.

Решение.
Нарисуем схему движения.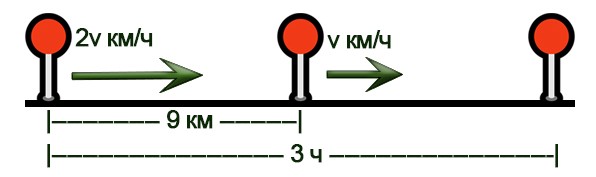

Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)

• Найдем скорость сближения туристов: 9:3=3 км/ч.
• По формуле сближения получаем: 2v-v=3  → v=3 →2v=6 км/ч.
• Ответ: 6

Задача 10. Скорость удаления

Два велосипедиста выехали из одного места в одном направлении. Скорость первого – 10 км/ч, а второго – 18 км/ч. Через сколько часов расстояние между велосипедистами будет равно 104 км?

Решение.
Нарисуем схему движения.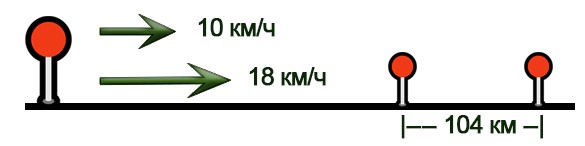

Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)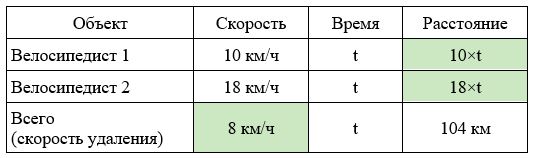

• Найдем скорость удаления: 18-10=8 км/ч
• Найдем время в пути: 108:8=13 часов.
• Ответ: 13

Задача 11. Скорость удаления

Два велосипедиста выехали в одном направлении из мест, находящихся на расстоянии 13 км друг от друга. Скорость первого – 12 км/ч, а второго – 17 км/ч, причем второй находился в начале движения впереди. Через сколько часов расстояние между велосипедистами будет равно 58 км?

Решение.
Нарисуем схему движения.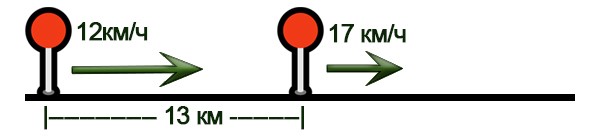

Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)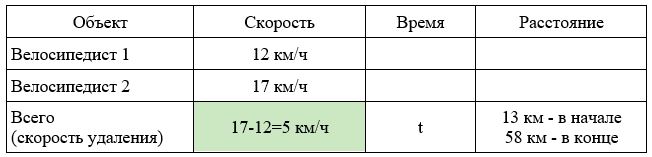

• Найдем скорость удаления: 17-12=5 км/ч
• Найдем расстояние, на которое они удались друг от друга: 58-13=45 км.
• Найдем время: 45:5=9 часов. 

Задача 12. Уровень ЕГЭ

Два кота одновременно выбегают в одном направлении из одного и того же подъезда. Скорость первого на 0,5 км/ч больше скорости второго. Через сколько минут расстояние между котами станет равным 200 метрам?

Решение.
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)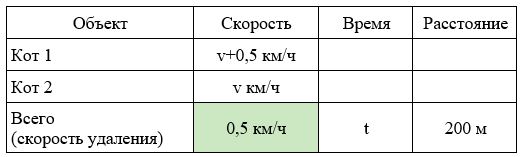

• Скорость удаления будет 0,5 км/ч — это скорость, с которой первый кот бежит быстрее второго.
• Найдем время: 0,2 : 0,5 = 0,4 часа
• Переведем время в другие единицы измерения: 0,4 ч = 0,4*60 = 24 мин.

Решить задачи на движение по реке

Задача 13.

Яхта движется по стоячей воде, ее собственная скорость равна 30 км/ч. Встречный ветер каждую минуту сносит яхту на 20 метров. За сколько часов яхта пройдет 259200 метров?

Решение.
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)

• Переведем скорость яхты в другие единицы измерения: 30 км/ч = 500 м/с.
• Найдем скорость удаления: 500-20=480 м/с.
• Найдем время: 259200 :480=540 минут = 9 часов.

Задача 14.

Расстояние от пристани А до пристани Б по течению реки катер прошёл за 5 часов, а на обратный путь он затратил на 1 час больше. Найдите скорость катера в неподвижной воде (собственную скорость), если скорость течения реки 2 км/ч. 

Решение.
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)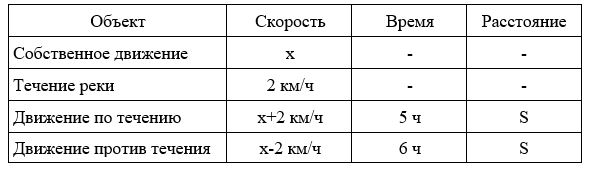

• Пусть скорость катера в неподвижной воде равна x км/ч.
• Составим уравнение: 5×(x+2)=6×(x-2); x=22 км/ч.

Правильность решения задач вы можете проверить на сайте intmag24.ru с помощью калькулятора решения задач на движение.

Советы для решения задач на движения

• В процессе решения задач на движение может быть составлена формула квадратного уравнения, которое будет иметь два корня. В этом случае нужно взять тот ответ, который  будет логичен для задачи (положительный). Отрицательный корень не берется во внимание.
• Внимательно следите, чтобы в задаче все данные измерялись одними величинами. Если это не так, нужно се привести к единым единицам измерения.