Задачи с процентами часто попадаются в экзаменационных заданиях. Многих они сбивают с толку – как разобраться с условием и как это решить? И совершенно зря, потому что с задачами на проценты каждый часто встречается в обычной жизни.
Пока такие задачки остаются оторванными от реальности строчками в учебнике, их бывает сложно понять и тем более решить. Чтобы стало понятнее, мы вам сейчас покажем примеры из обычной жизни, где вам могут встретиться проценты. А еще просто и доступно объясним, как решать задачи на проценты. И все у вас станет на свои места.
Задачи про проценты вокруг нас
Давайте оглядимся по сторонам: значения в процентах указаны на упаковках с любыми продуктами. Значок процента «%» смотрит на нас с рекламных плакатов скидок и распродаж. В новостях проценты сразу бросаются в глаза, когда речь идет о повышении цен на товары или коммунальные услуги. Разве вы сможете расшифровать все эти послания, если не научитесь решать задачи с процентами? Но вы, конечно, научитесь – мы в вас верим.
А вот такая ситуация: вы купили что-нибудь через интернет и получили извещение от ближайшего почтового отделения. Или сами собираетесь послать подарок другу в другой город. Вам обязательно надо уметь разбираться с процентами, чтобы узнать, сколько денег почта захочет получить за свои услуги по пересылке.
Или возьмем банковские кредиты и ипотеку. Банки в договорах всегда пишут мелкими буквами всякие вещи, которые полезно понимать. Например, какой процент по кредиту придется заплатить банку кроме тех денег, которые вы у него «одолжили» и обязаны вернуть.
А самый близкий школьникам пример связан с ЕГЭ. Каждый год после экзаменов публикуют официальную статистику. В которой немало задействованы и проценты. И эти проценты имеют прямое отношение к будущим выпускникам. Например, процент ребят, сдавших экзамен по математике на «хорошо» и «отлично» косвенно говорит о том, сколько абитуриентов с высокими баллами могли подать документы в вузы на технические специальности. А еще на программирование, прикладную математику и т.п. Чем их больше, тем выше конкурс. Если сравнивать их результаты со своими оценками, можно прикинуть собственные шансы на поступление.
Что такое процент?
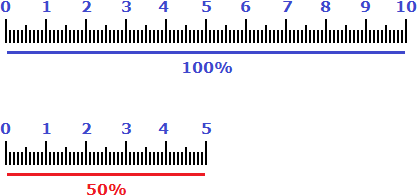
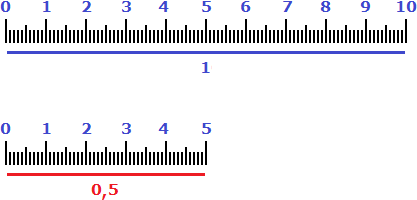
Самое очевидное определение: процент – это десятичная дробь. В жизни редко что-то можно сравнивать целиком, чаще приходится сравнивать разные части чего-то целого. Поэтому мы используем такие понятия, как половина (1/2), треть (1/3), четверть (1/4). Ну да, все так привыкли к слову «четверть» в школе, что забывают о его формальном значении – «четвертая часть учебного года». Сравнивать сотые доли удобнее всего – так появился процент (1/100): pro centum – «за сто» на латыни.
Все задачи по математике на проценты вертятся вокруг сравнения частей одного целого, определения, какую долю составляет часть от целого, нахождения целого исходя из величины его части и т.п.
Проценты можно записать со знакомым всем значком процента: 1%. Можно представить в виде десятичной дроби (или натурального числа). Для этого нужно разделить на 100: 0,01. Можно наоборот: выразить число в процентах. Тогда его следует умножить на 100%.
Типы задач на проценты
Раз мы уже договорились, что задачи на проценты – это задачи на дроби, такой тактики будем придерживаться и дальше.
Тип 1: Находим процент (дробь) от числа.
- Задача. За месяц на предприятии изготовили 500 приборов. 20% изготовленных приборов не смогли пройти контроль качества. Сколько приборов не прошло контроль качества?
- Решение. Нужно найти 20% от общего количества изготовленных приборов (500). 20% = 0,2. 500 * 0,2 = 100. 100 из общего количества изготовленных приборов контроль не прошло.
Тип 2: Находим число по его проценту (дроби).
- Задача. Готовясь к экзамену, школьник решил 38 задач из пособия для самоподготовки. Что составляет 23% числа всех задач в пособии. Сколько всего задач собрано в этом пособии для самоподготовки?
- Решение. Мы не знаем, сколько всего задача в пособии. Но зато нам известно, что 38 задач составляют 25% от общего их количества. Запишем 23% в виде дроби: 0,23. Далее нам следует известную нам часть целого разделить на ту долю, которую она составляет от всего целого: 38/0,25 = 38 * 100/25 = 152. Именно 152 задачи включили в этот сборник.
Тип 3: Находим процентное отношение двух чисел (часть от целого числа).
- Задача. В классе 30 учеников. 14 из них – девочки. Сколько процентов девочек в классе?
- Решение. Чтобы узнать, какой процент составляет одно число от другого, нужно то число, которое требуется найти, разделить на общее количество и умножить на 100%. Значит, 14/30*100% = 7/15*100% = 7*100%/15 = 47%.
Тип 4: Увеличиваем число на процент.
- Задача. На прошлогоднем экзамене по математике 140 старшеклассников получили пятерки. В этом году число отличников выросло на 15%. Сколько человек получили пятерки за экзамен по математике в этом году?
- Решение. Если некое число а увеличено на х%, то оно увеличилось в (1 + х /100) раз. Откуда а * (1 + х /100). Подставим в эту формулу данные нам по условию задачи цифры и получим ответ: 140 * (1 + 15/100) = 161.
Тип 5: Уменьшаем число на процент.
- Задача. Год назад школу закончили 100 ребят. А в это году выпускников на 25 меньше. Сколько выпускников в этом году?
- Решение. Если число а уменьшено на х% и при этом 0 ≤ х ≤ 100, то число уменьшено в (1 – х/100) раз. И нужное нам число находим по формуле а * (1 – х/100). Подставляем цифры из условия задачи и получаем ответ: 100 * (1 – 25/100) = 75.
Тип 6: Задачи на простые проценты.
- Задача. Родители взяли в банке кредит 5000 рублей сроком на год под 15% ежемесячно. Сколько денег они заплатят банку через год?
- Решение. Простые проценты называются так, потому что они начисляются многократно, но всякий раз к исходной сумме. Если обозначить исходную сумму как а, сумму, которая наращивается, как S, процентную ставку как х% и количество периодов начисления процента как у, то формулу можно записать так: S = а * (1 + у * х/100). Теперь подставим сюда цифры из условия задачи и узнаем, сколько денег родители заплатят банку: S = 5000 * (1 + 12 * 15/100) = 14000.
Тип 7: Задачи на сложные проценты.
- Задача. На этот раз сумма кредита 25000 рублей, взятых под те же 15% сроком на 3 месяца. Снова надо узнать, сколько денег придется заплатить банку по истечении срока кредита.
- Решение. Сложные проценты отличаются от простых тем, что процент много раз начисляется не к исходной сумме, а к сумме с уже начисленными раньше процентами. Пускай снова S – наращиваемая сумма, а – исходная, х% – процентная ставка, у – количество периодов начисления процента. В этом случае формула принимает вид: S = а * (1 + х/100)у. Подставляем цифры из условия: S = 25000 * (1 + 15/100)3 = 38021,875 – искомая сумма.
Кстати, простые задачи на проценты можно очень легко решать с помощью пропорции. Этот метод наглядный и дает такой же результат, так что выбирать можно каждому тот способ решения, который кажется проще. Давайте решим задачу №3 про класс и процент девочек в нем, составив пропорцию.
- Решение. Обозначим искомый процент девочек в классе как х, общее количество учеников примем за 100%. Пропорция выглядит так:
30 – 100%
14 – х%
Перемножим крест накрест левую и правую части пропорции и получим, что 30* х = 14 * 100 («30 относится к х также, как 14 относится к 100»). Откуда найти х уже совсем несложно: х = 14 * 100/30 = 47%.
Задачи на проценты с решением
Давайте решим несколько задач для подготовки к ЕГЭ. Как вы сами видите, решать их совсем несложно. Сейчас просто закрепим материал.
Задача 1. После открытия торгов на бирже в понедельник акции некой компании выросли в цене на неизвестное количество процентов. А во вторник на то же самое количество процентов упали в цене. В итоге они подешевели на 4% по отношению к своей первоначальной стоимости в понедельник. На какой процент акции этой компании поднимались в цене в понедельник?
Решение. Пускай первоначальная стоимость акций это 1. В понедельник акции дорожают на х * 100%. Их стоимость в это время: 1 + х * 1. Во вторник акции дешевеют на х * 100%. Их стоимость после этого: 1 + х – х * (1 + х). После чего они стали дешевле на 4%, т.е. стали стоить 0,96.
Отсюда 1 + х – х * (1 + х) = 0,96 ↔1 – х2 = 0,96 ↔ х2 = 0,04 ↔ х = 0,2. Т.е. в понедельник акции компании дорожали на 20%.
Задача 2. Четыре пары брюк дешевле одного пальто на 8%. Подсчитайте, на сколько процентов пять пар брюк стоят дороже, чем одно пальто.
Решение. Исходя из условия задачи, стоимость четырех пар брюк – это 92% от стоимости пальто. Легко подсчитать, что стоимость одной пары брюк – это 23% стоимости пальто (92/4 = 23). Теперь умножим стоимость одной пары брюк на пять и узнаем, что пять пар брюк обойдутся в 115% стоимости пальто (23 * 5 = 115). Т.е. пять пар брюк на 15% дороже, чем одно пальто.
Задача 3. Семья состоит из трех человек: муж, жена и дочь-студентка. Если зарплата мужа вырастет в два раза, общий доход семьи возрастет на 67%. Если дочери в три раза урежут стипендию, общий доход этой семьи уменьшится на 4%. Надо вычислить, какой процент в общий доход семьи приносит заработок жены.
Решение. Из условия следует, что общий доход семьи находится в прямой зависимости от доходов мужа. Не так важно, насколько ему поднимут зарплату. В любом случае общий доход семьи вырастет на 67%. Значит, зарплата мужа составляет как раз эти 67% от общего дохода. Если стипендия дочери уменьшится в три раза (т.е. на 1/3), останется 2/3 – это и есть 4%, на которые уменьшился бы семейных доход. Можно составить простую пропорцию и выяснить, что раз 2/3 стипендии – это 4% дохода, то вся стипендия – это 6%. А теперь отнимем от всего дохода вклад мужа и дочери и узнаем, какой процент составляет заработок жены в общем доходе семьи: 100% – 67% – 6% = 27%.
Задача 4. В емкости находится 5 литров водного раствора с концентраций вещества, равной 12%. В емкость добавили еще 7 литров воды. Раствор какой концентрации (с каким процентным содержанием вещества) получился после этого?
Решение. Опишем концентрацию вещества в растворе такой формулой: С = Vвещества/ Vраствора * 100%. Изначально в растворе содержится 0,12 * 5 = 0,6 литра вещества. Когда были добавлены 7 литров воды, объем раствора в емкости увеличился. Но концентрация вещества понизилась (его объем остался неизменным). Подставим все известные нам цифры в формулу и получим ответ: 0,6/5 + 7 *100% = 0,6 /12 * 100% = 5%.
Задача 5. В свежих абрикосах 90% влаги, а в кураге, которая из них получается, только 5%. Сколько килограммов абрикосов нужно, чтобы получить 20 килограммов кураги?
Решение. Исходя из условия, в абрикосах 10% питательного вещества, а в кураге оно содержится в концентрированном виде – 95%. Поэтому в 20 килограммах кураги 20 * 0,95 = 19 кг питательного вещества. На вопрос задачи мы ответим, если разделим одинаковое количество питательного вещества, которое содержится в разных объемах свежих абрикосов и кураги, на его процентное содержание в абрикосах. Чтобы получить 20 килограммов кураги, нужно взять 19/0,1 = 190 килограммов свежих абрикосов.
Заключение
Сами видите, решать задачи на проценты не так уж сложно. Если усвоить основные правила и подключить воображение, вы сможете щелкать такие задачки как орешки.
Вы даже можете составить задачу на проценты сами по нашим образцам. Кстати, будет очень хорошо, если вы так и поступите. Можете оставить нам свои задачи в комментариях – пускай другие наши читатели решат ваши задачи. А вы сможете решить те, что придумают они. Чтобы задач для подготовки к экзаменам получилось больше, расскажите про эту статью своим друзьям в социальных сетях.
Вот увидите, задачи на проценты вам придется решать еще много раз даже после того, как вы закончите школу. Они встречаются в физике, химии, биологии. Да и в повседневной жизни умение решать их может не раз пригодится. Не бойтесь сложных задач – мы всегда поможем вам найти к ним ключ.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Как посчитать процент от числа
- Главная
- /
- Математика
- /
- Арифметика
- /
- Как посчитать процент от числа
Чтобы найти процент от числа или определить сколько процентов число составляет от другого числа, надо воспользоваться пропорцией или нашим онлайн калькулятором:
Онлайн калькулятор
Сколько будет % от числа ?
Ответ:
0
Для того чтобы найти процент от числа, нужно просто это число умножить на число процентов и разделить на 100%.
Сколько процентов число составляет от числа ?
Ответ:
0
%
Чтобы определить сколько процентов число составляет от другого числа, необходимо первое число умножить на 100% и разделить на второе.
Число это % от какого числа?
Ответ:
0
Для того чтобы выяснить от какого числа другое число (X) составляет определённое количество процентов, надо число X умножить на 100% и разделить на количество интересующих вас процентов.
Теория
Сколько будет P% от числа Y?
Формула
X = (Y*P)/100
Пример
К примеру, определим сколько будет 12% от 600?
X = (600*12)/100
Ответ: X = 72
Сколько процентов число X составляет от числа Y?
Формула
P = (X*100)/Y
Пример
К примеру, определим сколько процентов число 72 составляет от 600?
P = (72*100)/600
Ответ: P = 12%
Число X это P% от какого числа?
Формула
Y = (100*X)/P
Пример
К примеру, определим: число 72 это 12% от какого числа?
Y = (100*72)/12
Ответ: Y = 600
Сколько процентов составляет одно число от другого
Онлайн калькулятор вычисляет сколько процентов составляет число от другого числа. Расчёт производится через пропорции.
Значащих цифр:
Сколько % составляет число
от числа
Как найти сколько процентов составляет одно число от другого
Чтобы вычислить сколько процентов составляет число от другого числа, нужно первое число умножить на 100% и разделить на второе число.
Разберём пример:
Вычислить сколько процентов составляет число 30 от числа 60.
30 * 100% / 60 = 50%
Эту задачу можно также решить через пропорцию
60 – 100%
30 – x
Из пропорции следует что x = 30 * 100% / 60 = 50%
Формула вычисления процента числа от числа
Разберём пример:
Найдём сколько процентов составляет число 40 от числа 200
40 * 100% / 200 = 20%
Похожие калькуляторы
7. Текстовые задачи базового уровня сложности
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи на нахождение процента по числу
В парке посажены три вида деревьев: березы, дубы и клены. Березы составляют 24(%) от всех деревьев, 880 деревьев — это дубы, а всего деревьев — 1375 штук. Сколько процентов составляют клены от всех деревьев?
1 способ.
Так как березы составляют (24%) от 1375 деревьев, то берез (1375cdot 0,24=330) штук. Следовательно, кленов (1375-330-880=165) штук. Тогда количество процентов, которое составляют клены от всех деревьев, равно [dfrac{165}{1375}cdot 100%=12%]
2 способ.
Дубы составляют от общего числа деревьев [dfrac{880}{1375}cdot
100%=64%] Следовательно, клены составляют (100%-24%-64%=12%).
Ответ: 12
Масса топлива ракеты до старта составляла 280 тонн. Через некоторое время часть топлива сгорела и масса оставшегося топлива стала 238 тонн. На сколько процентов уменьшилась масса топлива?
Сгорело (280 – 238 = 42) тонны топлива. Чтобы найти, сколько процентов от 280 составляет 42, надо разделить 42 на 280 и умножить на 100(%): (42 : 280 cdot 100% = 15%).
Ответ: 15
Масса палки колбасы до того, как её заметил Артем Я., составляла 1,2 килограмма. Артем Я. кое-что сделал с колбасой, после чего масса оставшейся части палки колбасы стала 0,75 килограмма. На сколько процентов уменьшилась масса палки колбасы?
Артем Я. куда-то дел (1,2 – 0,75 = 0,45) килограмма колбасы. Чтобы найти, сколько процентов от 1,2 составляет 0,45, надо разделить 0,45 на 1,2 и умножить на 100(%): (0,45 : 1,2 cdot 100 % = 37,5%).
Ответ: 37,5
Объем воды в графине до того, как его заметил Коля, составлял 2 литра. Коля выпил часть воды так, что оставшийся объем составил 1,3 литра. На сколько процентов уменьшился объем воды в графине?
Коля выпил (2 – 1,3 = 0,7) литра воды. Чтобы найти, сколько процентов от 2 составляет 0,7, надо разделить 0,7 на 2 и умножить на 100(%): (0,7 : 2 cdot 100% = 35%).
Ответ: 35
В прошлом году цена рубашки составляла 1300 рублей, а цена футболки 700 рублей. В этом году цена рубашки выросла на 35(%), а цена футболки выросла на 29(%). На сколько процентов больше нужно заплатить за комплект из рубашки и футболки в этом году по сравнению с прошлым годом?
Рубашка теперь стоит (1300 cdot (1 + 0,35) = 1755) рублей. Футболка стала стоить (700 cdot (1 + 0,29) = 903) рубля. Рубашка и футболка вместе стоят (1755 + 903 = 2658) рублей. В прошлом году комплект стоил (1300 + 700 = 2000) рублей, тогда его цена увеличилась в этом году на (dfrac{2658}{2000}cdot 100% – 100% = 32,9%).
Ответ: 32,9
В прошлом году цена трусов составляла 250 рублей, а цена пары носков 50 рублей. В этом году цена трусов выросла на 20(%), а цена пары носков выросла на 10(%). На сколько процентов больше нужно заплатить за комплект из двух трусов и десяти пар носков в этом году, чем в прошлом?
Трусы теперь стоят (250 cdot (1 + 0,2) = 300) рублей. Пара носков стала стоить (50 cdot (1 + 0,1) = 55) рублей. Комплект из двух трусов и десяти пар носков стоит (2cdot 300 + 10cdot 55 = 1150) рублей. В прошлом году такой комплект стоил (2cdot 250 + 10cdot 50
= 1000) рублей, тогда его цена увеличилась в этом году на (dfrac{1150}{1000}cdot 100% – 100% = 15%).
Ответ: 15
В прошлом году в кинотеатре “Фильм” цена большого ведра попкорна составляла 200 рублей, а цена банки колы 50 рублей. В этом году цена большого ведра попкорна выросла на 27(%), а цена банки колы выросла на 18(%). На сколько процентов больше нужно заплатить за набор из трёх больших вёдер попкорна и восьми банок колы в этом году, чем в прошлом?
Большое ведро попкорна теперь стоит (200 cdot (1 + 0,27) = 254) рубля. Банка колы стала стоить (50 cdot (1 + 0,18) = 59) рублей. Набор из трёх больших вёдер попкорна и восьми банок колы стоит (3cdot 254 + 8cdot 59 = 1234) рубля. В прошлом году такой набор стоил (3cdot 200 + 8cdot 50 = 1000) рублей, тогда его цена увеличилась в этом году на (dfrac{1234}{1000}cdot 100% – 100% =
23,4%).
Ответ: 23,4

УСТАЛ? Просто отдохни
Продолжаем изучать элементарные задачи по математике. Данный урок посвящен задачам на проценты. Мы рассмотрим несколько задач, а также затронем те моменты, которые не упоминали ранее при изучении процентов, посчитав что на первых порах они создают трудности для обучения.
Большинство задач на проценты сводятся к тому, чтобы найти процент от числá, найти число по проценту, выразить в процентах какую-либо часть, либо выразить в процентном соотношении взаимосвязь между несколькими объектами, числами, величинами.
Способы нахождения процента
Процент можно находить различными способами. Самый популярный способ — разделить число на 100 и умножить полученный результат на искомое количество процентов.
Например, чтобы найти 60% от 200 рублей, нужно сначала эти 200 рублей разделить на сто равных частей:
200 руб : 100 = 2 руб.
Когда мы делим число на 100, мы тем самым находим один процент от этого числа. Так, разделив 200 рублей на 100 частей, мы автоматически нашли 1% от двухсот рублей, то есть узнали сколько рублей прихóдится на одну часть. Как видно из примера, на одну часть (на один процент) приходится 2 рубля.
1% от 200 рублей — 2 рубля
Зная сколько рублей приходится на одну часть (на 1%), можно узнать сколько рублей приходится на две части, на три, на четыре, на пять и т.д. То есть можно найти любое количество процентов. Для этого достаточно умножить эти 2 рубля на искомое количество частей (процентов). Давайте найдём шестьдесят частей (60%)
2 руб × 60 = 120 руб.
Найдём 5%
2 руб × 5 = 10 руб.
Найдем 90%
2 руб × 90 = 180 руб.
Найдем 100%
2 руб × 100 = 200 руб.
100% это все сто частей и они составляют все 200 рублей.
Второй способ заключается в том, чтобы представить проценты в виде обыкновенной дроби и найти эту дробь от того числа, откуда требуется найти процент.
Например, найдем те же 60% от 200 рублей. Сначала предстáвим 60% в виде обыкновенной дроби. 60% это шестьдесят частей из ста, то есть шестьдесят сотых:
![]()
Теперь задание можно понимать как «найти ![]() от 200 рублей«. Это нахождение дроби от числа, которое мы изучали ранее. Напомним, что для нахождения дроби от числа, нужно это число разделить на знаменатель дроби и полученный результат умножить на числитель дроби
от 200 рублей«. Это нахождение дроби от числа, которое мы изучали ранее. Напомним, что для нахождения дроби от числа, нужно это число разделить на знаменатель дроби и полученный результат умножить на числитель дроби
200 : 100 = 2
2 × 60 = 120
Либо умножить число на дробь (быстрый способ нахождения дроби от числа):
![]()
Третий способ заключается в том, чтобы представить процент в виде десятичной дроби и умножить число на эту десятичную дробь.
Например, найдем те же 60% от 200 рублей. Для начала представляем 60% в виде дроби. 60% процентов это шестьдесят частей из ста
![]()
Выполним деление в этой дроби. Перенесем запятую в числе 60 на две цифры влево:
![]()
Теперь находим 0,60 от 200 рублей. Для нахождения десятичной дроби от числа, нужно это число умножить на десятичную дробь:
200 × 0,60 = 120 руб.
Приведенный способ нахождения процента является наиболее удобным, особенно если человек привык пользоваться калькулятором. Этот способ позволяет найти процент в одно действие.
Как правило выразить процент в десятичной дроби не составляет особого труда. Достаточно приписать «ноль целых» перед процентной долей, если процентная доля представляет собой двузначное число, или приписать «ноль целых» и еще один ноль, если процентная доля представляет собой однозначное число. Примеры:
60% = 0,60 — приписали ноль целых перед числом 60, поскольку число 60 является двузначным
6% = 0,06 — приписали ноль целых и еще один ноль перед числом 6, поскольку число 6 является однозначным.
При делении на 100 мы воспользовались методом передвижения запятой на две цифры влево. В ответе 0,60 ноль, стоящий после цифры 6, сохранился. Но если выполнить это деление уголком, ноль исчезает — получается ответ 0,6
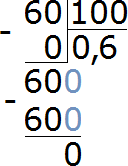
Надо помнить, что десятичные дроби 0,60 и 0,6 равны одному и тому же значению:
0,60 = 0,6
В том же «уголке» можно продолжать деление бесконечно, каждый раз приписывая к остатку ноль, но это будет бессмысленным действием:

Выражать проценты в виде десятичной дроби можно не только делением на 100, но и умножением. Значок процента (%) сам по себе заменяет собой множитель 0,01. А если учитывать, что число процентов и значок процента записаны слитно, то между ними располагается «невидимый» знак умножения (×).
Так, запись 45% на самом деле выглядит следующим образом:
![]()
Заменим знак процента на множитель 0,01
![]()
Данное умножение на 0,01 выполнятся путем перемещения запятой на две цифры влево:
![]()
Задача 1. Бюджет семьи составляет 75 тыс. рублей в месяц. Из них 70% — деньги, заработанные папой. Какую часть заработала мама?
Решение
Всего процентов 100. Если папа заработал 70% денег, то остальные 30% денег заработала мама.
Задача 2. Бюджет семьи составляет 75 тыс. рублей в месяц. Из них 70% — деньги, заработанные папой, а 30% — деньги, заработанные мамой. Сколько денег заработал каждый?
Решение
Найдем 70 и 30 процентов от 75 тыс. рублей. Так мы определим сколько денег заработал каждый. Для удобства 70% и 30% запишем в виде десятичных дробей:
75 × 0,70 = 52,5 (тыс. руб. заработал папа)
75 × 0,30 = 22,5 (тыс. руб. заработала мама)
Проверка
52,5 + 22,5 = 75
75 = 75
Ответ: 52,5 тыс. руб. заработал папа, 22,5 руб. заработала мама.
Задача 3. При остывании хлеб теряет до 4% своей массы в результате испарения воды. Сколько килограммов испарится при остывании 12 тонн хлеба.
Решение
Переведем 12 тонн в килограммы. В одной тонне тысяча килограмм, а в 12 тоннах в 12 раз больше:
1000 × 12 = 12 000 кг
Теперь найдем 4% от 12000. Полученный результат и будет ответом к задаче:
12 000 × 0,04 = 480 кг
Ответ: при остывании 12 тонн хлеба испарится 480 килограмм.
Задача 4. Яблоки при сушке теряют 84% своей массы. Сколько получится сушенных яблок из 300 кг свежих?
Найдем 84% от 300 кг
300 : 100 × 84 = 252 кг
300 кг свежих яблок в результате сушки потеряют 252 кг своей массы. Чтобы ответить на вопрос сколько получится сушенных яблок, нужно из 300 вычесть 252
300 − 252 = 48 кг
Ответ: из 300 кг свежих яблок получится 48 кг сушенных.
Задача 5. В семенах сои содержится 20% масла. Сколько масла содержится в 700 кг сои?
Решение
Найдем 20% от 700 кг
700 × 0,20 = 140 кг
Ответ: в 700 кг сои содержится 140 кг масла
Задача 6. Гречневая крупа содержит 10% белков, 2,5% жиров и 60% углеводов. Сколько этих продуктов содержится в 14,4 ц гречневой крупы?
Решение
Переведем 14,4 центнера в килограммы. В одном центнере 100 килограмм, в 14,4 центнерах в 14,4 раз больше
100 × 14,4 = 1440 кг
Найдем 10%, 2,5% и 60% от 1440 кг
1440 × 0,10 = 144 (кг белков)
1440 × 0,025 = 36 (кг жиров)
1440 × 0,60 = 864 (кг углеводов)
Ответ: в 14,4 ц гречневой крупы содержится 144 кг белков, 36 кг жиров, 864 кг углеводов.
Задача 7. Для лесопитомника школьники собрали 60 кг семян дуба, акации, липы и клена. Желуди составляли 60%, семена клена 15%, семена липы 20% всех семян, а остальное составляли семена акации. Сколько килограммов семян акации было собрано школьниками?
Решение
Примем за 100% семена дуба, акации, липы и клена. Вычтем из этих 100% проценты, выражающие семена дуба, липы и клена. Так мы узнаем сколько процентов составляют семена акации:
100% − (60% + 15% + 20%) = 100% − 95% = 5%
Теперь находим семена акации:
60 × 0,05 = 3 кг
Ответ: школьниками было собрано 3 кг семян акации.
Проверка:
60 × 0,60 = 36
60 × 0,15 = 9
60 × 0,20 = 12
60 × 0,05 = 3
36 + 9 + 12 + 3 = 60
60 = 60
Задача 8. Купил человек продукты. Молоко стоит 60 рублей, что составляет 48% от стоимости всех покупок. Определить общую сумму денег, потраченных на продукты.
Решение
Это задача на нахождение числа по его проценту, то есть по его известной части. Такую задачу можно решать двумя способами. Первый заключается в том, чтобы выразить известное число процентов в виде десятичной дроби и найти неизвестное число по этой дроби
Выразим 48% в виде десятичной дроби
48% : 100 = 0,48
Зная, что 0,48 составляет 60 рублей, мы можем определить сумму всех покупок. Для этого нужно найти неизвестное число по десятичной дроби:
60 : 0,48 = 125 рублей
Значит, общая сумма денег, затраченных на продукты составляет 125 рублей.
Второй способ заключается в том, чтобы сначала узнать сколько денег приходится на один процент, затем полученный результат умножить на 100
48% это 60 рублей. Если мы разделим 60 рублей на 48, то узнаем сколько рублей приходится на 1%
60 : 48% = 1,25 рублей
На 1% приходится 1,25 рублей. Всего процентов 100. Если мы умножим 1,25 рублей на 100, получим общую сумму денег, затраченных на продукты
1,25 × 100 = 125 рублей
Задача 9. Из свежих слив выходит 35% сушенных. Сколько надо взять свежих слив, чтобы получить 140 кг сушенных? Сколько получится сушенных слив из 600 кг свежих?
Решение
Выразим 35% в виде десятичной дроби и найдем неизвестное число по этой дроби:
35% = 0,35
140 : 0,35 = 400 кг
Чтобы получить 140 кг сушенных слив, нужно взять 400 кг свежих.
Ответим на второй вопрос задачи — сколько получится сушенных слив из 600 кг свежих? Если из свежих слив выходит 35% сушенных, то достаточно найти эти 35% от 600 кг свежих слив
600 × 0,35 = 210 кг
Ответ: чтобы получить 140 кг сушенных слив, нужно взять 400 кг свежих. Из 600 кг свежих слив получится 210 кг сушенных.
Задача 10. Усвоение жиров организмом человека составляет 95%. За месяц ученик употребил 1,2 кг жиров. Сколько жиров может быть усвоено его организмом?
Решение
Переведем 1,2 кг в граммы
1,2 × 1000 = 1200 г
Найдем 95% от 1200 г
1200 × 0,95 = 1140 г
Ответ: 1140 г жиров может быть усвоено организмом ученика.
Выражение чисел в процентах
Процент, как было сказано ранее, можно представить в виде десятичной дроби. Для этого достаточно разделить число этих процентов на 100. Например, представим 12% в виде десятичной дроби:
![]()
Замечание. Мы сейчас не находим процент от чего-то, а просто записываем его в виде десятичной дроби.
Но возможен и обратный процесс. Десятичная дробь может быть представлена в виде процента. Для этого нужно умножить эту дробь на 100 и поставить знак процента (%)
Представим десятичную дробь 0,12 в виде процентов
0,12 × 100 = 12%
Это действие называют выражением числа в процентах или выражением чисел в сотых долях.
Умножение и деление являются обратными операциями. К примеру, если 2 × 5 = 10, то 10 : 5 = 2

Точно так же деление можно записать в обратном порядке. Если 10 : 5 = 2, то 2 × 5 = 10:
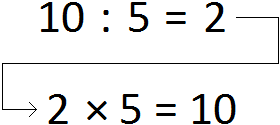
Тоже самое происходит, когда мы выражаем десятичную дробь в виде процентов. Так, 12% были выражены в виде десятичной дроби следующим образом: 12 : 100 = 0,12 но потом эти же 12% были «возвращены» с помощью умножения, записав выражение 0,12 × 100 = 12%.
Аналогично можно выразить в процентах любые другие числа, в том числе и целые. Например, выразим в процентах число 3. Умножим данное число на 100 и к полученному результату добавим знак процента:
3 × 100 = 300%
Большие проценты вида 300% поначалу могут сбивать с толку, поскольку человек привык считать 100% максимальной долей. Из дополнительных сведений о дробях мы знаем, что один целый объект можно обозначать через единицу. К примеру, если имеется целый не разрезанный торт, то его можно обозначить через 1
Этот же торт можно обозначить как 100% торта. В этом случае и единица и 100% будут обозначать один и тот же целый торт:

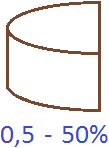
Разрежем торт пополам. В этом случае единица обратится в десятичное число 0,5 (поскольку это половина единицы), а 100% обратятся в 50% (поскольку 50 это половина от сотни)
Вернем обратно целый торт, единицу и 100%

Изобразим ещё два таких торта с такими же обозначениями:
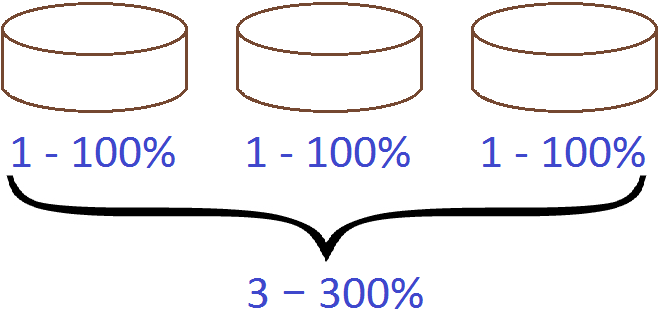
Если один торт является единицей, то три торта являются тремя единицами. Каждый торт является целым стопроцентным. Если сложить эти три сотни получится 300%.
Поэтому при переводе целых чисел в проценты, мы умножаем эти числа на 100.
Задача 2. Выразить в процентах число 5
5 × 100 = 500%
Задача 3. Выразить в процентах число 7
7 × 100 = 700%
Задача 4. Выразить в процентах число 7,5
7,5 × 100 = 750%
Задача 5. Выразить в процентах число 0,5
0,5 × 100 = 50%
Задача 6. Выразить в процентах число 0,9
0,9 × 100 = 90%
Пример 7. Выразить в процентах число 1,5
1,5 × 100 = 150%
Пример 8. Выразить в процентах число 2,8
2,8 × 100 = 280%
Задача 9. Джордж идет со школы домой. Первые пятнадцать минут он прошел 0,75 пути. В остальное время он прошел оставшиеся 0,25 пути. Выразите в процентах части пути, пройденные Джорджом.
Решение
0,75 × 100 = 75%
0,25 × 100 = 25%
Задача 10. Джона угостили половиной яблока. Выразите эту половину в процентах.
Решение
Половина яблока записывается в виде дроби 0,5. Чтобы выразить эту дробь в процентах, умножим её на 100 и к полученному результату добавим знак процента
0,5 × 100 = 50%
Аналоги в виде дробей
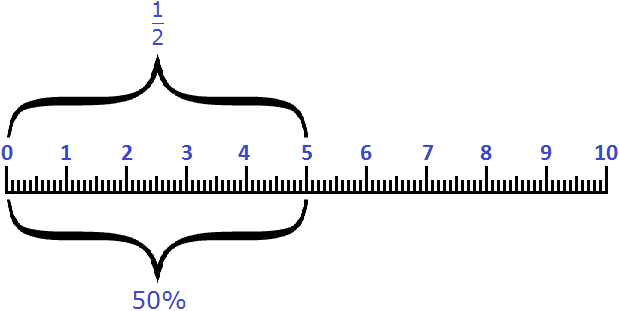
Величина, выраженная в процентах, имеет свой аналог в виде обычной дроби. Так, аналогом для 50% является дробь ![]() . Пятьдесят процентов также можно назвать словом «половина».
. Пятьдесят процентов также можно назвать словом «половина».
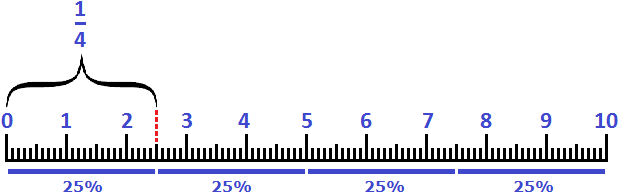
Аналогом для 25% является дробь ![]() . Двадцать пять процентов также можно назвать словом «четверть».
. Двадцать пять процентов также можно назвать словом «четверть».
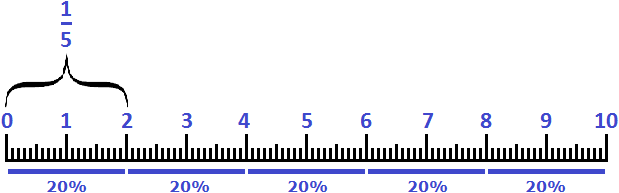
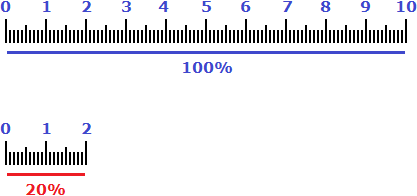
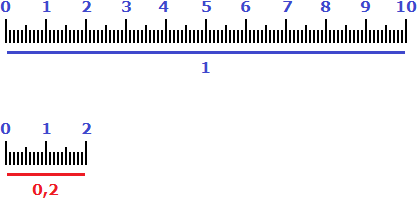
Аналогом для 20% является дробь ![]() . Двадцать процентов также можно назвать словами «пятая часть».
. Двадцать процентов также можно назвать словами «пятая часть».
Аналогом для 40% является дробь ![]() .
.
Аналогом для 60% является дробь ![]()
Пример 1. Пять сантиметров это 50% от дециметра или ![]() или же просто половина. Во всех случаях речь идет об одной и той же величине — пяти сантиметрах из десяти
или же просто половина. Во всех случаях речь идет об одной и той же величине — пяти сантиметрах из десяти
Пример 2. Два с половиной сантиметра это 25% от дециметра или ![]() или же просто четверть
или же просто четверть
Пример 3. Два сантиметра это 20% от дециметра или ![]()
Пример 4. Четыре сантиметра это 40% от дециметра или ![]()
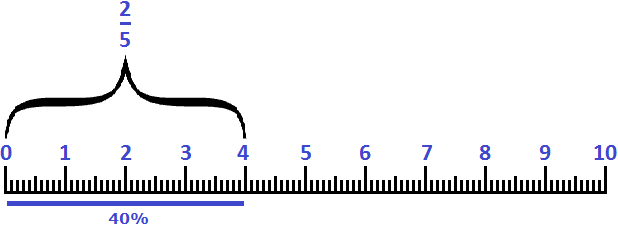
Пример 5. Шесть сантиметров это 60% от дециметра или ![]()
Уменьшение и увеличение процентов
При увеличении или уменьшении величины, выраженной в процентах употребляется предлог «на».
Примеры:
- Увеличить на 50% — означает увеличить величину в 1,5 раза;
- Увеличить на 100% — означает увеличить величину в 2 раза;
- Увеличить на 200% — означает увеличить в 3 раза;
- Уменьшить на 50% — означает уменьшить величину в 2 раза;
- Уменьшить на 80% — означает уменьшить в 5 раз.
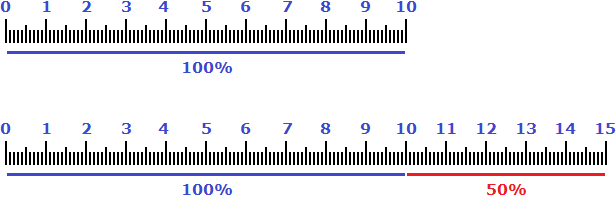
Пример 1. Десять сантиметров увеличили на 50%. Сколько сантиметров получилось?
Чтобы решать подобные задачи, нужно исходную величину принимать за 100%. Исходная величина это 10 см. 50% от них составляют 5 см
Изначальные 10 см увеличили на 50% (на 5 см), значит получилось 10+5 см, то есть 15 см
Аналогом же увеличения десяти сантиметров на 50% является множитель 1,5. Если умножить на него 10 см получится 15 см
10 × 1,5 = 15 см
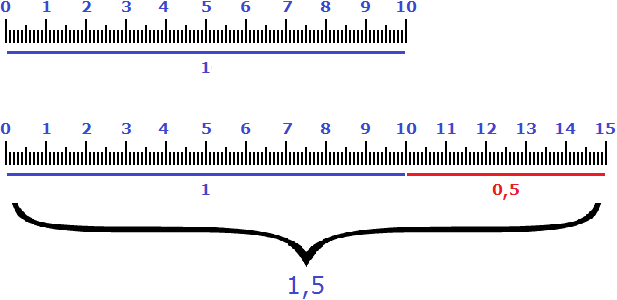
Поэтому выражения «увеличить на 50%» и «увеличить в 1,5 раза» говорят об одном и том же.
Пример 2. Пять сантиметров увеличили на 100%. Сколько сантиметров получилось?
Примем исходные пять сантиметров за 100%. Сто процентов от этих пяти сантиметров будут сами 5 см. Если увеличить 5 см на эти же 5 см, то получится 10 см
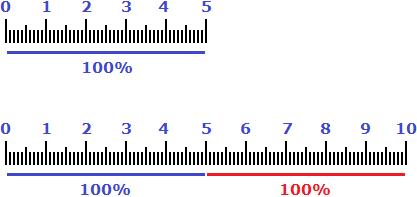
Аналогом же увеличения пяти сантиметров на 100% является множитель 2. Если умножить на него 5 см получится 10 см
5 × 2 = 10 см
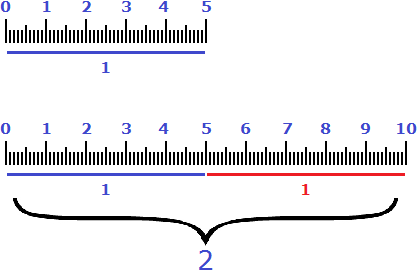
Поэтому выражения «увеличить на 100%» и «увеличить в 2 раза» говорят об одном и том же.
Пример 3. Пять сантиметров увеличили на 200%. Сколько сантиметров получилось?
Примем исходные пять сантиметров за 100%. Двести процентов это два раза по сто процентов. То есть 200% от 5 см будут составлять 10 см (по 5 см на каждые 100%). Если увеличить 5 см на эти 10 см, то получится 15 см
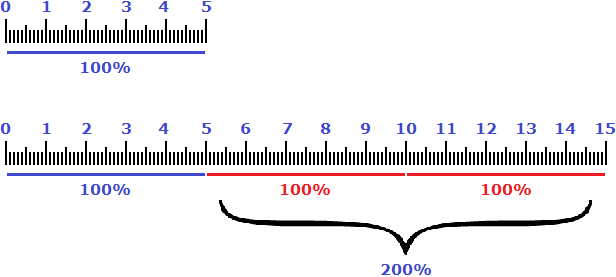
Аналогом же увеличения пяти сантиметров на 200% является множитель 3. Если умножить на него 5 см получится 15 см
5 × 3 = 15 см
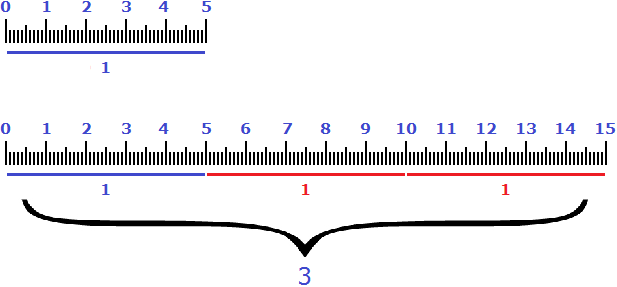
Поэтому выражения «увеличить на 200%» и «увеличить в 3 раза» говорят об одном и том же.
Пример 4. Десять сантиметров уменьшили на 50%. Сколько сантиметров осталось?
Примем исходные 10 см за 100%. Пятьдесят процентов от 10 см составляют 5 см. Если уменьшить 10 см на эти 5 см, останется 5 см
Аналогом же уменьшения десяти сантиметров на 50% является делитель 2. Если разделить на него 10 см, то получится 5 см
10 : 2 = 5 см
Поэтому выражения «уменьшить на 50%» и «уменьшить в 2 раза» говорят об одном и том же.
Пример 5. Десять сантиметров уменьшили на 80%. Сколько сантиметров осталось?
Примем исходные 10 см за 100%. Восемьдесят процентов от 10 см составляют 8 см. Если уменьшить 10 см на эти 8 см, останется 2 см
Аналогом же уменьшения десяти сантиметров на 80% является делитель 5. Если разделить на него 10 см, то получится 2 см
10 : 5 = 2 см
Поэтому выражения «уменьшить на 80%» и «уменьшить в 5 раз» говорят об одном и том же.
При решении задач на уменьшение и увеличение процентов, можно умножать/делить величину на указанный в задаче множитель.
Задача 1. Насколько процентов изменилась величина, если она увеличилась в 1,5 раза?
Величину о которой говорится в задаче можно обозначить как 100%. Далее умножить эти 100% на множитель 1,5
100% × 1,5 = 150%
Теперь из полученных 150% вычтем изначальные 100% и получим ответ к задаче:
150% − 100% = 50%
Задача 2. Насколько процентов изменилась величина, если она уменьшилась в 4 раза?
В этот раз будет происходить уменьшение величины, поэтому будем выполнять деление. Величину о которой говорится в задаче обозначим как 100%. Далее разделим эти 100% на делитель 4
100% : 4 = 25%
Из изначальных 100% вычтем полученные 25% и получим ответ к задаче:
100% − 25% = 75%
Значит, при уменьшении величины в 4 раза она уменьшилась на 75%.
Задача 3. Насколько процентов изменилась величина, если она уменьшилась в 5 раз?
Величину о которой говорится в задаче обозначим как 100%. Далее разделим эти 100% на делитель 5
100% : 5 = 20%
Из изначальных 100% вычтем полученные 20% и получим ответ к задаче:
100% − 20% = 80%
Значит, при уменьшении величины в 5 раз она уменьшилась на 80%.
Задача 4. Насколько процентов изменилась величина, если она уменьшилась в 10 раз?
Величину о которой говорится в задаче обозначим как 100%. Далее разделим эти 100% на делитель 10
100% : 10 = 10%
Из изначальных 100% вычтем полученные 10% и получим ответ к задаче:
100% − 10% = 90%
Значит, при уменьшении величины в 10 раз она уменьшилась на 90%.
Задача на нахождение процентного соотношения
Чтобы выразить что-либо в процентном соотношении, сначала нужно записать дробь, показывающую какую часть первое число составляет от второго, затем выполнить деление в этой дроби и полученный результат выразить в процентах.
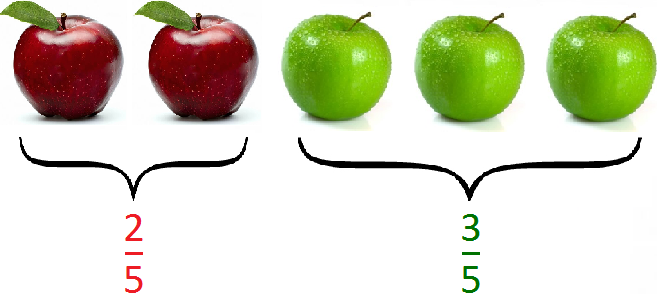
Например, пусть имеется пять яблок. При этом два яблока являются красными, три — зелеными. Выразим красные и зеленые яблоки в процентном соотношении.
Сначала нужно узнать какую часть составляют красные яблоки. Всего яблок пять, а красных два. Значит, два из пяти или две пятых составляют красные яблоки:

Зеленых же яблок три. Значит, три из пяти или три пятых составляют зеленые яблоки:
Имеем две дроби ![]() и
и ![]() . Выполним деление в этих дробях
. Выполним деление в этих дробях
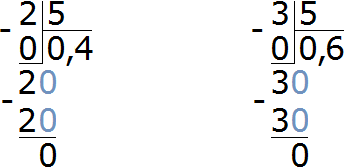
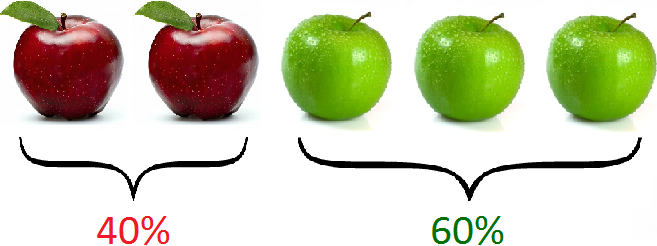
Получили десятичные дроби 0,4 и 0,6. Теперь выразим в процентах эти десятичные дроби:
0,4 × 100 = 40%
0,6 × 100 = 60%
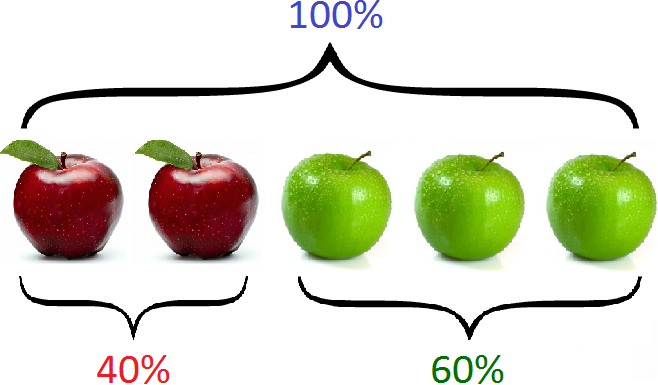
Значит, 40% составляют красные яблоки, 60% — зеленые.
А все пять яблок составляют 40%+60%, то есть 100%
Задача 2. Двум сыновьям мама дала 200 рублей. Младшему брату мама дала 80 рублей, а старшему 120 рублей. Выразите в процентном соотношении деньги, данные каждому брату.
Решение
Младший брат получил 80 рублей из 200 рублей. Записываем дробь восемьдесят двухсотых:
![]()
Старший брат получил 120 рублей из 200 рублей. Записываем дробь сто двадцать двухсотых:
![]()
Имеем дроби ![]() и
и ![]() . Выполним деление в этих дробях
. Выполним деление в этих дробях
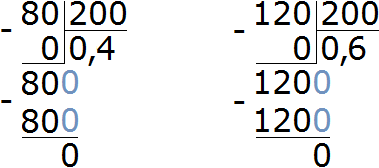
Выразим в процентах полученные результаты:
0,4 × 100 = 40%
0,6 × 100 = 60%
Значит, 40% денег получил младший брат, а 60% — старший.
Некоторые дроби, показывающие какую часть первое число составляет от второго, можно сокращать.
Так дроби ![]() и
и ![]() можно было бы сократить. От этого ответ к задаче не изменился бы:
можно было бы сократить. От этого ответ к задаче не изменился бы:
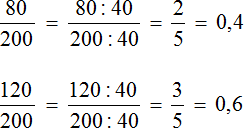
Задача 3. Бюджет семьи составляет 75 тыс. рублей в месяц. Из них 52,5 тыс. руб. — деньги, заработанные папой. 22,5 тыс. руб. — деньги, заработанные мамой. Выразите в процентах деньги, заработанные папой и мамой.
Решение
Данная задача, как и предыдущая, является задачей на нахождение процентного соотношения.
Выразим в процентах деньги, заработанные папой. Он заработал 52,5 тыс. рублей из 75 тыс. рублей
![]()
Выполним деление в этой дроби:
![]()
Выразим полученный результат в процентах:
0,7 × 100 = 70%
Значит, папа заработал 70% денег. Далее нетрудно догадаться, что остальные 30% денег заработала мама. Ведь 75 тыс. рублей это все 100% денег. Для уверенности сделаем проверку. Мама заработала 22,5 тыс. руб. из 75 тыс. руб. Записываем дробь, выполняем деление и выражаем в процентах полученный результат:
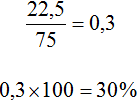
Задача 4. Школьник тренируется делать подтягивания на перекладине. В прошлом месяце он мог делать 8 подтягиваний за подход. В этом месяце он может делать 10 подтягиваний за подход. На сколько процентов он увеличил количество подтягиваний?
Решение
Узнаем на сколько больше подтягиваний школьник делает в текущем месяце, чем в прошлом
10 − 8 = 2
Узнаем какую часть два подтягивания составляют от восьми подтягиваний. Для этого найдем отношение 2 к 8
![]()
Выполним деление в этой дроби
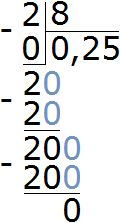
Выразим полученный результат в процентах:
0,25 × 100 = 25%
Значит, школьник увеличил количество подтягиваний на 25%.
Эту задачу можно решить и вторым, более быстрым методом — узнать во сколько раз 10 подтягиваний больше, чем 8 подтягиваний и полученный результат выразить в процентах.
Чтобы узнать во сколько раз десять подтягиваний больше восьми подтягиваний, нужно найти отношение 10 к 8
![]()
Выполним деление в получившейся дроби
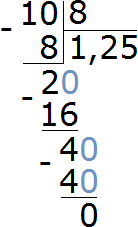
Выразим полученный результат в процентах:
1,25 × 100 = 125%
Показатель подтягиваний в текущем месяце составляет 125%. Данное высказывание нужно понимать именно как «составляет 125%», а не как «показатель увеличился на 125%». Это два разных высказывания, выражающих различные количества.
Высказывание «составляет 125%» нужно понимать как «восемь подтягиваний, которые составляют 100% плюс два подтягивания, которые составляют 25% от восьми подтягиваний». Графически это выглядит следующим образом:
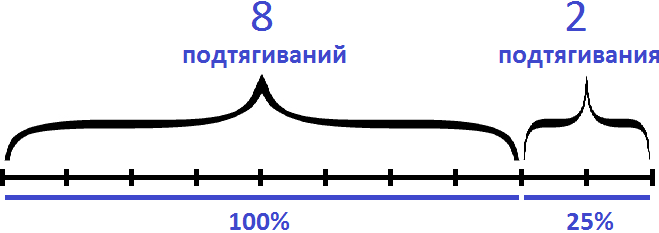
А высказывание «увеличился на 125%» нужно понимать как «к текущим восьми подтягиваниях, которые составляли 100% добавились еще 100% (еще 8 подтягиваний) плюс еще 25% (2 подтягивания)». Итого получается 18 подтягиваний
100% + 100% + 25% = 8 + 8 + 2 = 18 подтягиваний
Графически это высказывание выглядит следующим образом:
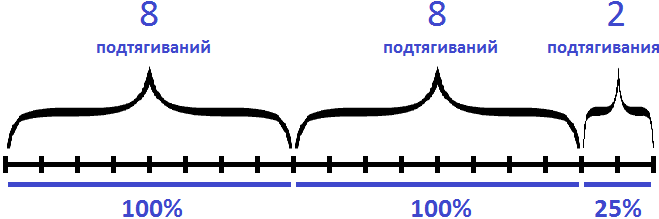
Всего же получается 225%. Если найти 225% от восьми подтягиваний, мы получим 18 подтягиваний
8 × 2,25 = 18
Задача 5. В прошлом месяце зарплата составляла 19,2 тыс. руб. В текущем месяце она составила 20,16 тыс. руб. На сколько процентов повысилась зарплата?
Эту задачу как и предыдущую можно решать двумя способами. Первый заключается в том, чтобы сначала узнать на сколько рублей увеличилась зарплата. Далее узнать какую часть эта прибавка составляет от зарплаты прошлого месяца
Узнаем на сколько рублей повысилась зарплата:
20,16 − 19,2 = 0,96 тыс. руб.
Узнаем какую часть 0,96 тыс. руб. составляет от 19,2. Для этого найдем отношение 0,96 к 19,2
![]()
Выполним деление в получившейся дроби. По пути вспомним, как выполняется деление десятичных дробей:
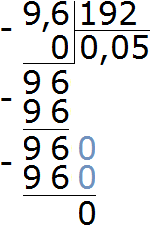
Выразим полученный результат в процентах:
0,05 × 100 = 5%
Значит, зарплата повысилась на 5%.
Решим задачу вторым способом. Узнаем во сколько раз 20,16 тыс. руб. больше, чем 19,2 тыс. руб. Для этого найдем отношение 20,16 к 19,2
![]()
Выполним деление в получившейся дроби:
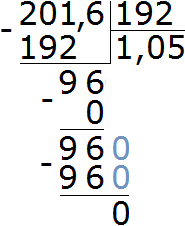
Выразим полученный результат в процентах:
1,05 × 100 = 105%
Зарплата составляет 105%. То есть сюда входят 100%, которые составляли 19,2 тыс. руб., плюс 5% которые составляют 0,96 тыс. руб.
100% + 5% = 19,2 + 0,96
Задача 6. Цена ноутбука в этом месяце повысилась на 5%. Какова его цена, если в прошлом месяце он стоил 18,3 тыс. рублей?
Решение
Найдем 5% от 18,3:
18,3 × 0,05 = 0,915
Прибавим эти 5% к 18,3:
18,3 + 0,915 = 19,215 тыс. руб.
Ответ: цена ноутбука составляет 19,215 тыс. руб.
Задача 7. Цена ноутбука в этом месяце снизилась на 10%. Какова его цена, если в прошлом месяце он стоил 16,3 тыс. рублей?
Решение
Найдем 10% от 16,3:
16,3 × 0,10 = 1,63
Вычтем эти 10% из 16,3:
16,3 − 1,63 = 14,67 (тыс. рублей)
Подобные задачи можно записывать кратко:
16,3 − (16,3 × 0,10) = 14,67 (тыс. рублей)
Ответ: цена ноутбука составляет 14,67 тыс. рублей.
Задача 8. В прошлом месяце цена ноутбука составляла 21 тыс. рублей. В этом месяце цена повысилась до 22,05 тыс. рублей. На сколько процентов повысилась цена?
Решение
Определим насколько рублей повысилась цена
22,05 − 21 = 1,05 (тыс. руб)
Узнаем какую часть 1,05 тыс. руб. составляет от 21 тыс. руб.
![]()
Выразим полученный результат в процентах
0,05 × 100 = 5%
Ответ: цена ноутбука повысилась на 5%
Задача 8. Рабочий должен был изготовить по плану 600 деталей, а он изготовил 900 деталей. На сколько процентов он выполнил план?
Решение
Узнаем во сколько раз 900 деталей больше, чем 600 деталей. Для этого найдем отношение 900 к 600
![]()
Значение данной дроби равно 1,5. Выразим это значение в процентах:
1,5 × 100 = 150%
Значит, рабочий выполнил план на 150%. То есть выполнил его на все 100%, изготовив 600 деталей. Затем изготовил еще 300 деталей, что составляет 50% от изначального плана.
Ответ: рабочий выполнил план на 150%.
Сравнение величин в процентах
Мы уже много раз сравнивали величины различными способами. Первым нашим инструментом была разность. Так, к примеру чтобы сравнить 5 рублей и 3 рубля, мы записывали разность 5−3. Получив ответ 2, можно было сказать, что «пять рублей больше трех рублей на два рубля».
Получаемый в результате вычитания ответ в повседневной жизни называют не «разностью», а «разницей».
Так, разница между пятью и тремя рубля составляет два рубля.
Следующим инструментом, которым мы воспользовались для сравнения величин, было отношение. Отношение позволяло нам узнать во сколько раз первое число больше второго (или сколько раз первое число содержит второе).
Так, к примеру десять яблок больше двух яблок в пять раз. Или по другому, десять яблок содержит два яблока пять раз. Данное сравнение можно записать с помощью отношения
![]()
Но величины можно сравнить и в процентах. Например, цену двух товаров сравнивать не в рублях, а оценивать, насколько цена одного товара больше или меньше цены другого в процентах.
Для сравнения величин в процентах, одну из них нужно обозначить как 100%, а вторую исходя из условий задачи.
Например, узнаем на сколько процентов десять яблок больше, чем восемь яблок.
За 100% нужно обозначить ту величину с которой мы что-либо сравниваем. Мы сравниваем 10 яблок с 8 яблоками. Значит, за 100% обозначаем 8 яблок:

Теперь наша задача сравнить на сколько процентов 10 яблок больше, чем эти 8 яблок. 10 яблок это 8+2 яблока. Значит, добавив к восьми яблокам ещё два яблока, мы увеличим 100% еще на какое-то число процентов. Чтобы узнать на какое именно, определим сколько процентов от восьми яблок составляют два яблока
![]()
Добавив эти 25% к восьми яблокам, мы получим 10 яблок. А 10 яблок это 8+2, то есть 100% и еще 25%. Итого получаем 125%

Значит, десять яблок больше восьми яблок на 25%.
Теперь решим обратную задачу. Узнаем насколько процентов восемь яблок меньше, чем десять яблок. Сразу напрашивается ответ, что восемь яблок меньше на 25%. Однако это не так.
Мы сравниваем восемь яблок с десятью яблоками. Мы договорились, что за 100% будем брать то, с чем сравниваем. Поэтому в этот раз за 100% берем 10 яблок:

Восемь яблок это 10−2, то есть уменьшив 10 яблок на 2 яблока, мы уменьшим их на какое-то число процентов. Чтобы узнать на какое именно, определим сколько процентов от десяти яблок составляют два яблока
![]()
Отняв эти 20% от десяти яблок, мы получим 8 яблок. А 8 яблок это 10−2, то есть 100% и минус 20%. Итого получаем 80%
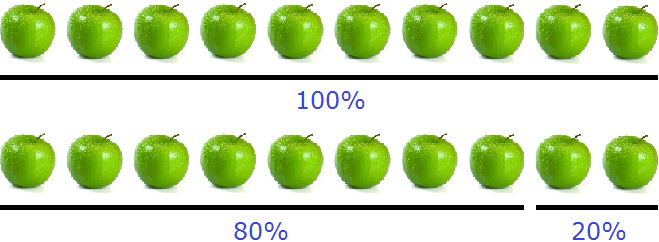
Значит, восемь яблок меньше десяти яблок на 20%.
Задача 2. На сколько процентов 5000 рублей больше, чем 4000 рублей?
Решение
Примем 4000 рублей за 100%. 5 тысяч больше 4 тысяч на 1 тысячу. Значит, увеличив четыре тысячи на одну тысячу, мы увеличим четыре тысячи на какое-то количество процентов. Узнаем на какое именно. Для этого определим какую часть одна тысяча составляет от четырех тысяч:
![]()
Выразим полученный результат в процентах:
0,25 × 100 = 25%
1000 рублей от 4000 рублей составляют 25%. Если прибавить эти 25% к 4000, то получится 5000 рублей. Значит, 5000 рублей на 25% больше, чем 4000 рублей
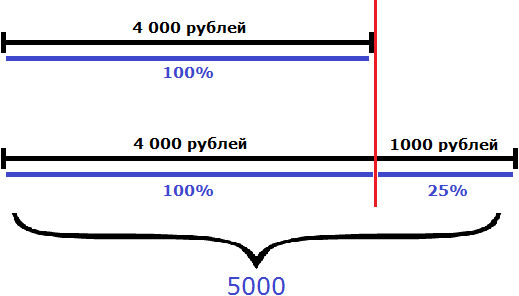
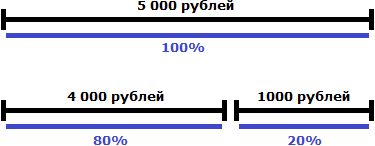
Задача 3. На сколько процентов 4000 рублей меньше, чем 5000 рублей?
В этот раз сравниваем 4000 с 5000. Примем 5000 за 100%. Пять тысяч больше четырех тысяч на одну тысячу рублей. Узнаем какую часть одна тысяча составляет от пяти тысяч
![]()
Тысяча от пяти тысяч составляет 20%. Если вычесть эти 20% от 5000 рублей, то получим 4000 рублей.
Значит, 4000 рублей меньше 5000 рублей на 20%
Задачи на концентрацию, сплавы и смеси
Допустим, возникло желание приготовить какой-нибудь сок. У нас в распоряжении имеется вода и малиновый сироп

Нальем 200 мл воды в стакан:
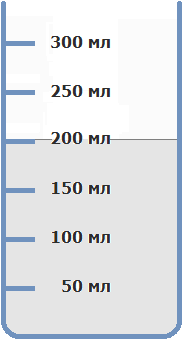
Добавим 50 мл малинового сиропа и размешаем полученную жидкость. В результате у нас получится 250 мл малинового сока (200 мл воды + 50 мл сиропа = 250 мл сока)
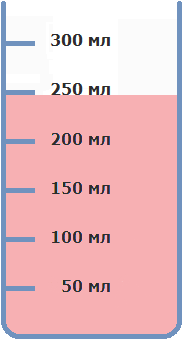
Какую часть от получившегося сока составляет малиновый сироп?
Малиновый сироп составляет ![]() сока. Вычислим это отношение, получим число 0,20. Это число показывает количество растворённого сиропа в получившемся соке. Назовём это число концентрацией сиропа.
сока. Вычислим это отношение, получим число 0,20. Это число показывает количество растворённого сиропа в получившемся соке. Назовём это число концентрацией сиропа.
Концентрацией растворённого вещества называют отношение количества растворённого вещества или его массы к объему раствора.
Концентрация обычно выражается в процентах. Давайте выразим концентрацию сиропа в процентах:
0,20 × 100 = 20%
Таким образом, концентрация сиропа в малиновом соке составляет 20%.
Вещества в растворе могут быть неоднородными. Например, смешаем 3 л воды и 200 г соли.
Масса 1 л воды составляет 1 кг. Тогда масса 3 л воды будет составлять 3 кг. Переведем 3 кг в граммы, получим 3 кг = 3000 г.
Теперь в 3000 г воды опустим 200 г соли и смешаем полученную жидкость. В результате получится соленный раствор, общая масса которого будет составлять 3000+200, то есть 3200 г. Найдем концентрацию соли в полученном растворе. Для этого найдём отношение массы растворенной соли к массе раствора
![]()
Значит, при смешивании 3 л воды и 200 г соли получится 6,25%-й раствор соли.
Аналогично может быть определено количество вещества в сплаве или в смеси. Например, сплав содержит олово массой 210 г, и серебро массой 90 г. Тогда масса сплава будет составлять 210+90, то есть 300 г. Олова в сплаве будет содержаться ![]() , а серебра
, а серебра ![]() . В процентном соотношении олова будет 70%, а серебра 30%
. В процентном соотношении олова будет 70%, а серебра 30%
При смешивании двух растворов получается новый раствор, состоящий из первого и второго растворов. У нового раствора концентрация вещества может быть другой. Полезным навыком является умение решать задачи на концентрацию, сплавы и смеси. В общем итоге смысл таких задач заключается в отслеживании изменений, которые происходят при смешивании растворов различной концентрации.
Смешаем два малиновых сока. Первый сок объемом 250 мл содержит 12,8% малинового сиропа. А второй сок объемом 300 мл содержит 15% малинового сиропа. Сольем эти два сока в большой стакан и смешаем. В результате получим новый сок объемом 550 мл.
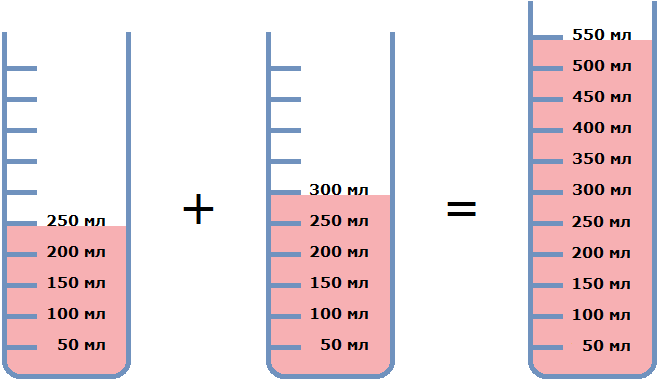
Теперь определим концентрацию сиропа в полученном соке. Первый слитый сок объемом 250 мл содержал 12,8% сиропа. А 12,8% от 250 мл это 32 мл. Значит, первый сок содержал 32 мл сиропа.
Второй слитый сок объемом 300 мл содержал 15% сиропа. А 15% от 300 мл это 45 мл. Значит, второй сок содержал 45 мл сиропа.
Сложим количества сиропов:
32 мл + 45 мл = 77 мл
Эти 77 мл сиропа содержатся в новом соке, объем которого составляет 550 мл. Определим концентрацию сиропа в этом соке. Для этого найдём отношение 77 мл растворённого сиропа к объему сока 550 мл:
![]()
Значит, при смешивании 12,8%-го малинового сока объемом 250 мл и 15%-го малинового сока объемом 300 мл, получается 14%-й малиновый сок объемом 550 мл.
Задача 1. Имеются 3 раствора морской соли в воде: первый раствор содержит 10% соли, второй содержит 15% соли и третий — 20% соли. Смешали 130 мл первого раствора, 200 мл второго раствора и 170 мл третьего раствора. Определите сколько процентов составляет морская соль в полученном растворе.
Решение
Определим объем полученного раствора:
130 мл + 200 мл + 170 мл = 500 мл
Поскольку в первом растворе было 130 × 0,10 = 13 мл морской соли, во втором растворе 200 × 0,15 = 30 мл морской соли, а в третьем — 170 × 0,20 = 34 мл морской соли, то в полученном растворе будет содержаться 13 + 30 + 34 = 77 мл морской соли.
Определим концентрацию морской соли в полученном растворе. Для этого найдём отношение 77 мл морской соли к объему раствора 500 мл
![]()
Значит, в полученном растворе содержится 15,4% морской соли.
Задача 2. Сколько граммов воды надо добавить к 50 г раствора, содержащего 8% соли, чтобы получить 5%-й раствор?
Решение
Заметим, что если к имеющемуся раствору добавить воды, то количество соли в нём не изменится. Изменится только её процентное содержание, поскольку добавление воды в раствор приведёт к изменению его массы.
Нам нужно добавить такое количество воды при котором восемь процентов соли стали бы пятью процентами.
Определим сколько граммов соли содержится в 50 г раствора. Для этого найдем 8% от 50
50 г × 0,08 = 4 г
8% от 50 г составляют 4 г. Другими словами, на восемь частей из ста приходятся 4 грамма соли. Давайте сделаем так, чтобы эти 4 грамма приходились не на восемь частей, а на пять частей, то есть на 5%
4 грамма — 5%
Теперь зная, что на 5% раствора приходятся 4 грамма, мы можем найти массу всего раствора. Для этого нужно найти число по его проценту:
4 г : 5 = 0,8 г
0,8 г × 100 = 80 г
80 граммов раствора это масса при которой 4 грамма соли будут приходиться на 5% раствора. А для получения этих 80 граммов, нужно к изначальным 50 граммам добавить 30 граммов воды.
Значит, для получения 5%-го раствора соли, нужно к имеющемуся раствору добавить 30 г воды.
Задача 2. Виноград содержит 91% влаги, а изюм – 7%. Сколько килограммов винограда требуется для получения 21 килограмма изюма?
Решение
Виноград состоит из влаги и чистого вещества. Если в свежем винограде содержится 91% влаги, то на остальные 9% будет приходиться чистое вещество этого винограда:

Изюм же содержит 93% чистого вещества и 7% влаги:

Заметим, что в процессе превращения винограда в изюм, исчезает только влага этого винограда. Чистое вещество остаётся без изменения. После того, как виноград превратится в изюм, в получившемся изюме будет 7% влаги и 93% чистого вещества.
Определим сколько чистого вещества содержится в 21 кг изюма. Для этого найдем 93% от 21 кг
21 кг × 0,93 = 19,53 кг
Теперь вернемся к первому рисунку. Наша задача состояла в том, чтобы определить сколько винограда нужно взять для получения 21 кг изюма. Чистое вещество массой 19,53 кг будет приходиться на 9% винограда:
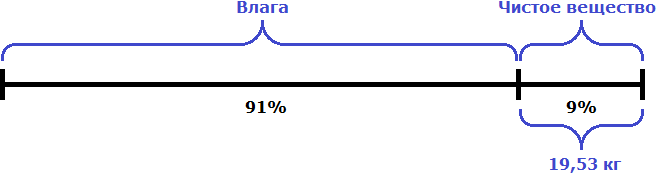
Теперь зная, что 9% чистого вещества составляют 19,53 кг, мы можем определить сколько винограда требуется для получения 21 кг изюма. Для этого нужно найти число по его проценту:
19,53 кг : 9 = 2,17 кг
2,17 кг × 100 = 217 кг
Значит, для получения 21 кг изюма нужно взять 217 кг винограда.
Задача 3. В сплаве олова и меди медь составляет 85%. Сколько надо взять сплава, чтобы в нём содержалось 4,5 кг олова?
Решение
Если в сплаве медь составляет 85%, то на остальные 15% будет приходиться олово:

Спрашивается сколько надо взять сплава, чтобы в нем содержалось 4,5 олова. Поскольку олова в сплаве содержится 15%, то 4,5 кг олова и будут приходиться на эти 15%.
А зная, что 4,5 кг сплава составляют 15% мы можем определить массу всего сплава. Для этого нужно найти число по его проценту:
4,5 кг : 15 = 0,3 кг
0,3 кг × 100 = 30 кг
Значит, сплава нужно взять 30 кг, чтобы в нём содержалось 4,5 кг олова.
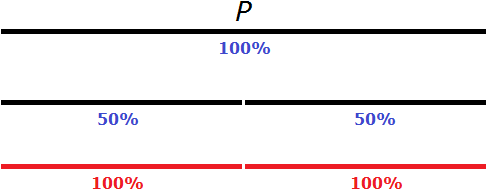
Задача 4. Смешали некоторое количество 12%-го раствора соляной кислоты с таким же количеством 20%-го раствора этой же кислоты. Найти концентрацию получившейся соляной кислоты.
Решение
Изобразим на рисунке первый раствор в виде прямой линии и выделим на нём 12%
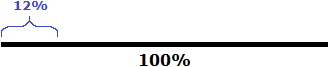
Поскольку количество растворов одинаково, рядом можно изобразить такой же рисунок, иллюстрирующий второй раствор с содержанием соляной кислоты 20%

У нас получилось двести частей раствора (100% + 100%), тридцать две части из которых составляют соляную кислоту (12% + 20%)
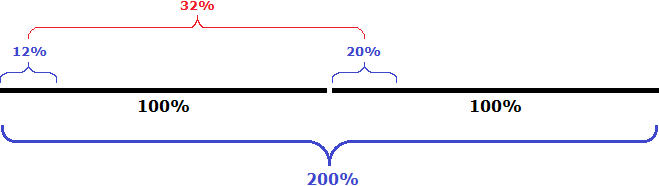
Определим какую часть 32 части составляют от 200 частей
![]()
Значит, при смешивании 12%-го раствора соляной кислоты с таким же количеством 20%-го раствора этой же кислоты получится 16%-й раствор соляной кислоты.
Для проверки представим, что масса первого раствора была 2 кг. Масса второго раствора так же будет составлять 2 кг. Тогда при смешивании этих растворов получится 4 кг раствора. В первом растворе соляной кислоты было 2 × 0,12 = 0,24 кг, а во втором — 2 × 0,20 = 0,40 кг. Тогда в новом растворе соляной кислоты будет 0,24 + 0,40 = 0,64 кг. Концентрация соляной кислоты составит 16%
![]()
Задачи для самостоятельного решения
Задание 1. Выразите в виде обыкновенной дроби следующие части:

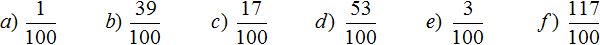
Задание 2. Выразите в виде обыкновенной дроби следующие части:
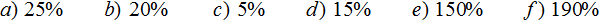
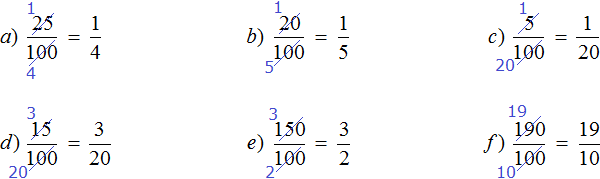
Задание 3. Выразите в виде десятичной дроби следующие части:


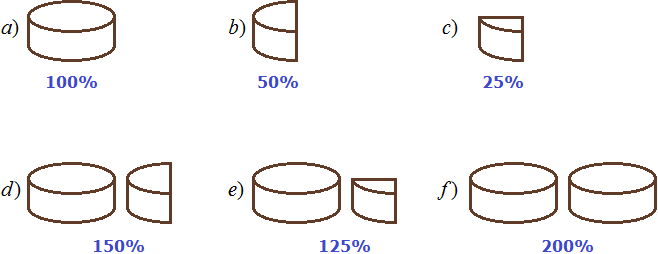
Задание 4. Изобразите графически следующие части:
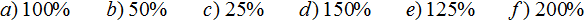
Задание 5. Опишите следующий рисунок в виде процентов:
Задание 6. Опишите следующий рисунок в виде процентов:
Задание 7. Опишите следующий рисунок в виде процентов:

Задание 8. Опишите следующий рисунок в виде процентов:
Задание 9. Опишите следующий рисунок в виде процентов:

Задача 10. Число 50 увеличили на 20%. Найти новое значение числа.
Решение
Найдем 20% от 50
50 × 0,20 = 10
Прибавим полученное число 10 к числу 50, получим новое значение 60
50 + 10 = 60
Ответ: новое значение равно 60.
Задача 11. Число увеличили на 60%. Найти новое значение числа.
Решение
Найдем 60% от и прибавим их к
. Так мы определим новое значение числа.
Для удобства нахождения шестидесяти процентов от , заменим 60% на его аналог в виде обыкновенной дроби
 . Умножив
. Умножив на
 , мы найдем 60% от числа
, мы найдем 60% от числа
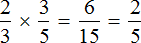
Теперь увеличим число на найденные 60%, т.е. на число

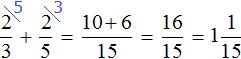
Ответ: новое значение равно 
Задача 12. Ответьте на следующие вопросы:
1) Потратили 80 % суммы. Сколько процентов этой суммы осталось?
2) Мужчины составляют 75 % всех работников завода. Сколько процентов работников завода составляют женщины?
3) Девочки составляют 40 % класса. Сколько процентов класса составляют мальчики?
Ответы
1) 20%
2) 25%
3) 60%
Задача 13. Ответьте на следующие вопросы:
1) В магазин привезли 2500 кг помидоров. В первый день продали 30% всех помидоров. Сколько килограммов помидоров осталось продать?
2) В школе 400 учащихся, 52 % этого числа составляют девочки. Сколько мальчиков в школе?
Задача 14. Число увеличили на 25%. На сколько процентов надо уменьшить новое число, чтобы получилось исходное?
Решение
Воспользуемся переменной. Пусть A это исходное число о котором говорится в задаче. Примем это исходное число А за 100%
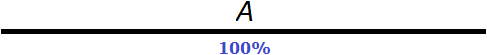
Увеличим это исходное число A на 25%

Теперь новое число составляет 125%. Узнаем какую часть от 125% составляет 25%. Для этого найдем отношение 25% к 125%
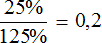
Выразим полученный результат в процентах:
0,2 × 100 = 20%

Ответ: чтобы получить исходное число, новое число надо уменьшить на 20%.
Задача 15. Число уменьшили на 50%. На сколько надо увеличить новое число, чтобы получилось исходное?
Решение
Воспользуемся переменной. Пусть P это исходное число о котором говорится в задаче. Примем это исходное число P за 100%
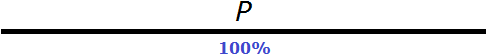
Уменьшим это исходное число P на 50%
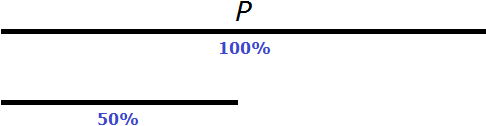
Теперь новое число составляет 50% от исходного числа. Узнаем во сколько раз исходное число P больше нового числа. Для этого найдем отношение 100% к 50%
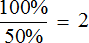
Исходное число в два раза больше нового. Это видно даже по рисунку. А чтобы сделать новое число равным исходному, его нужно увеличить в два раза. А увеличить число в два раза означает увеличить его на 100%.
Значит, новое число, которое составляет половину от исходного числа, нужно увеличить на 100%.
Рассматривая новое число, его также принимают за 100%. Так, на приведенном рисунке новое число является половиной от исходного числа и подписано как 50%. По отношению к исходному числу новое число является половиной. Но если рассматривать его отдельно от исходного, его нужно принимать за 100%.
Поэтому на рисунке, новое число которое изображается линией, сначала было обозначено как 50%. Но затем это число мы обозначили как 100%.
Ответ: чтобы получить исходное число, новое число надо увеличить на 100%.
Задача 16. В прошлом месяце в городе произошло 15 ДТП.
В этом месяце этот показатель снизился до 6. На сколько процентов снизилось количество ДТП?
Решение
В прошлом месяце было 15 ДТП. В этом месяце 6. Значит, количество ДТП снизилось на 9.
Примем 15 ДТП за 100%. Снизив 15 ДТП на 9, мы снизим их на какое-то число процентов. Чтобы узнать на какое именно, узнаем какую часть 9 ДТП составляет от 15 ДТП
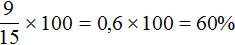
9 ДТП от 15 составляет 60%. Значит, количество ДТП снизилось на 60%.
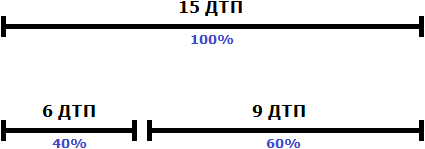
Ответ: количество ДТП снизилось на 60%.
Задача 17. Смешали 8 кг 18%-го раствора некоторого вещества с 12 кг 8%-го раствора этого же вещества. Найдите концентрацию получившегося раствора.
Решение
Сложим массы исходных растворов:
8 кг + 12 кг = 20 кг
В первом растворе было 8 × 0,18 = 1,44 кг вещества, а во втором растворе 12 × 0,08 = 0,96 кг этого же вещества. Тогда в получившемся растворе будет 1,44 + 0,96 = 2,40 кг.
Определим концентрацию вещества в получившемся растворе:
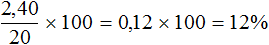
Ответ: концентрация получившегося раствора составляет 12%.
Задача 18. Смешали некоторое количество 11%-го раствора некоторого вещества с таким же количеством 19% раствора этого же вещества. Найдите концентрацию получившегося раствора.
Решение
Масса обоих растворов одинакова. Каждый раствор можно принять за 100%. После сложения растворов получится 200% раствора. В первом растворе было 11% вещества, а во втором 19% вещества. Тогда в получившемся 200%-м растворе будет 11% + 19% = 30% вещества.
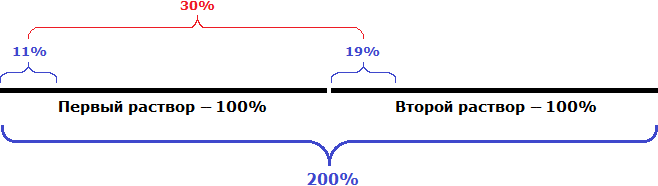
Определим концентрацию получившегося растворе. Для этого узнаем какую часть тридцать частей вещества составляют от двухсот частей вещества:
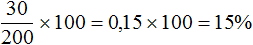
Ответ: концентрация получившегося раствора составляет 15%.
Задача 19. За последние 3 месяца цены на продукты питания росли в среднем на 10% за каждый месяц. На сколько процентов выросли цены за 3 месяца?
Решение
Примем первоначальную цену на продукты питания за 100%. Для удобства решения задачи, проценты будем выражать в десятичных дробях. Тогда 100% в виде десятичной дроби будут записаны как 1.
За первый месяц цена повысилась на 10%. Прибавим к имеющейся цене 1 десять процентов от этой цены, получим 1 + 0,10 × 1. Эта сумма равна выражению 1,10. Значит, цена за первый месяц станет 1,10.
За второй месяц цена также повысилась на 10%. Прибавим к нынешней цене 1,10 десять процентов от этой цены, получим 1,10 + 0,10 × 1,10. Эта сумма равна выражению 1,21. Значит, цена за второй месяц станет 1,21.
За третий месяц цена также повысилась на 10%. Прибавим к нынешней цене 1,21 десять процентов от этой цены, получим 1,21 + 0,10 × 1,21. Эта сумма равна выражению 1,331. Тогда цена за третий месяц станет 1,331.
Вычислим разницу между новой и старой ценой. Если изначальная цена была равна 1, то повысилась она на 1,331 − 1 = 0,331. Выразим этот результат в процентах, получим 0,331 × 100 = 33,1%
Ответ: за 3 месяца цены на продукты питания повысились на 33,1%.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже


