Задача как найти скорость каждого поезда

Ответ:

[Пусть x frac{км}{ч} – скорость товарного ]

[поезда;]

[(x + 20) frac{км}{ч} – скорость ]

[пассажирского поезда.]

[Пассажирский поезд проходит 120 км ]

[на 1 час быстрее, чем товарный.]

[Составим уравнение: ]

[frac{120}{x + 20} + 1 = frac{120}{x} text{ }| cdot x(x + 20)]

[ОДЗ: x neq 0; x neq – 20]

[120x + x(x + 20) = 120 cdot (x + 20)]

[120x + x^{2} + 20x = 120x + 2400]

[x^{2} + 140x – 120x – 2400 = 0]

[x^{2} + 20x – 2400 = 0]

[x_{1} + x_{2} = – 20; x_{1} cdot x_{2} = – 2400]

[x_{1} = 40 left( frac{км}{ч} right) – скорость товарного ]

[поезда. ]

[x_{2} = – 60 (не подходит).]

[x + 20 = 40 + 20 = 60 left( frac{км}{ч} right) – скорость ]

[пассажирского поезда.]

[Ответ:40 frac{км}{ч};60 frac{км}{ч}.]

Задачи на движение (скорость, время и расстояние) являются одной из основных типов задач по математике, которые должен уметь решать каждый школьник. В данной статье рассмотрены все типы задач на движение:
— простые задачи на скорость, время и расстояние;
— задачи на встречное и противоположное движение;
— задачи на движение в одном направлении (на сближение и удаление);
— решение задач на движение по реке.

Скорость, время и расстояние: определения, обозначения, формулы

скорость = расстояние: время — формула нахождения скорости;

время = расстояние: скорость — формула нахождения времени;

расстояние = скорость · время — формула нахождения расстояния.

Скорость – это расстояние, пройденное за единицу времени: за 1 секунду, за 1 минуту, за 1 час и так далее.
Пример обозначения: 7 км/ч (читается: семь километров в час).
Если весь путь проходится с одинаковой скоростью, то такое движение называется равномерным.

На сайте представлены калькуляторы онлайн, с помощью которых можно перевести скорость, время и расстояние в другие единицы измерения:

1.Конвертер единиц измерения скорости
2.Конвертер единиц измерения времени
3.Конвертер единиц измерения расстояния (длины)

Примеры простых задач.

Задача 1. 

Автомобиль проехал 180 км за 2 часа. Чему равна скорость автомобиля?
Решение: 180:2=90 (км/ч.)
Ответ: Скорость автомобиля равна 90 км/ч.

Задача 2. 

Автобус проехал путь в 240 км со скоростью 80 км/ч. Сколько времени ехал автобус?
Решение: 240:80=3 (ч.)
Ответ: Автобус проехал 3 часа.

Задача 3. 

Грузовик ехал 5 часов со скоростью 70 км/ч. Какое расстояние проехал грузовик за это время?
Решение: 70 · 3 = 350 (км)
Ответ: Грузовик за 5 часов проехал 350 км.

Задачи на встречное движение

В таких задачах два объекта движутся навстречу друг другу.
Задачи на встречное движение можно решать двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость сближения объектов (как сумму их скоростей), общие время и расстояние. Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.

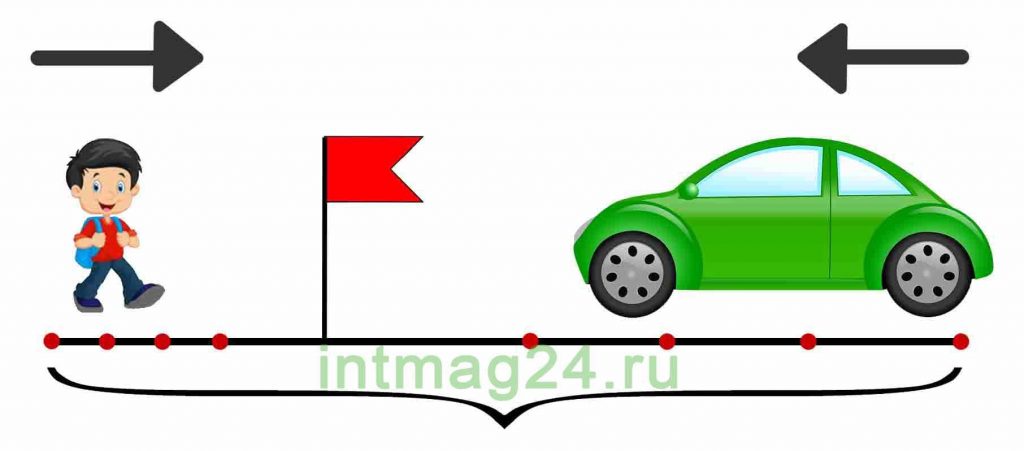
Задача 4. 

Из двух пунктов навстречу друг другу одновременно выехали два поезда и встретились через 3 часа. Первый поезд ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. На каком расстоянии друг от друга находятся пункты?
Решение: 
Первый способ. Найти расстояние, которое проехал каждый автобус, и сложить полученные данные:
80*3=240 (км) – проехал 1й автобус, 70*3=210 (км) – проехал 2й поезд,
240+210=450 (км) – проехали два поезда.
Второй способ. Найти скорость сближения поездов, то есть на сколько сокращалось расстояние между ними каждый час; а затем найти расстояние:
80+70=150 (км/ч), 150*3=450 (км).
Ответ: города находятся на расстоянии 450 км.

Задача 5. 

Из двух городов навстречу друг другу одновременно выехали два автобуса. Первый автобус ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. Какое расстояние будет между ними через 2 часа, если расстояние между городами 450 км?
Решение: 
Первый способ. Определить, сколько километров проехал каждый автобус и найти расстояние, которое осталось проехать:
80*2=160 (км)-проехал 1й автобус, 70*2=140 (км)-проехал 2й автобус,
160+140=300 (км)-проехали два автобуса, 450-300=150 (км)-осталось проехать.
Второй способ. Найти скорость сближения автобусов и умножить ее на время в пути.
80*70=150 (км/ч) – скорость сближения; 150*2=300 (км) – проехали два автобуса; 450-300=150 (км) – осталось проехать.
Ответ: Через 2часа расстояние между автобусами будет 150 км.

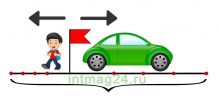
Задачи на движение в противоположных направлениях

В таких задачах два объекта движутся в противоположных направлениях, отдаляясь друг от друга. В таком типе задачи используется скорость удаления. Задачи на движение в противоположных направлениях также можно решить двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость удаления объектов (как сумму их скоростей), общие время и расстояние. Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.

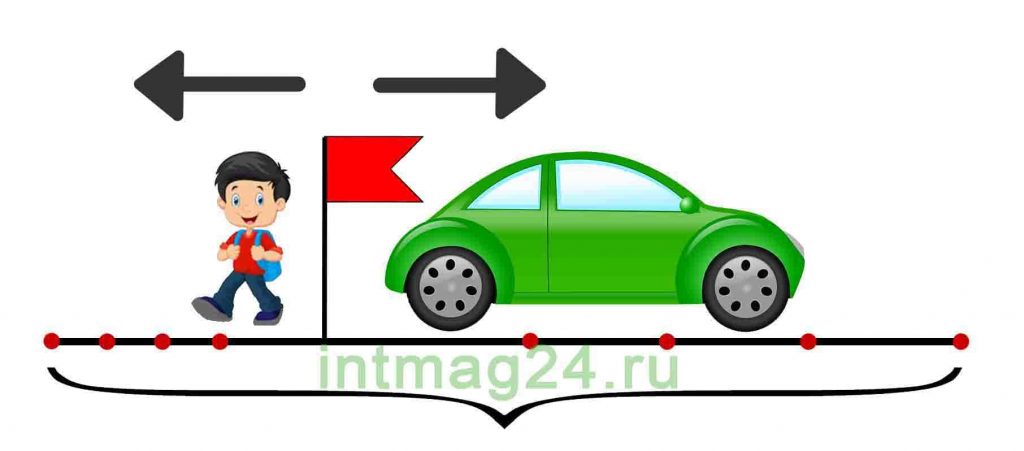
Задача 6. 

Два автомобиля выехали одновременно из одного и того же пункта в противоположных направлениях. Скорость первого автомобиля 100 км/ч, скорость второго – 70 км/ч. Какое расстояние будет между автомобилями через 4 часа?
Решение: 
Первый способ. Определить расстояние, которое проехал каждый автомобиль и найти сумму полученных результатов:
1) 100 · 4 = 400 (км) – проехал первый автомобиль
2) 70 · 4 = 280 (км) – проехал второй автомобиль
400 + 280 = 680 (км)
Второй способ. Найти скорость удаления, то есть значение увеличения расстояния между автомобилями за каждый час, а затем скорость удаления умножить на время в пути.
100 + 70= 170 км/ч – это скорость удаления автомобилей.
170 · 4 = 680 (км)
Ответ: Через 4 часа между автомобилями будет 680 км.

Задача 7. 

Из двух населённых пунктов, расстояние между которыми 40 км, вышли в противоположных направлениях два туриста. Первый турист шёл со скоростью 4 км/ч, а второй — 5 км/ч. Какое расстояние между туристами будет через 5 часов?
Решение: 
Первый способ. Определить сколько километров прошёл каждый из туристов за 5 часов, сложить полученные результаты, а затем к полученному расстоянию прибавить расстояние между населенными пунктами.
1) 4 · 5 = 20 (км) – прошёл первый турист;
2) 5 · 5 = 25 (км) – прошёл второй турист;
3) 20 + 25 = 45 (км);
4) 45 + 40 = 85 (км).
Второй способ. Найти скорость удаления пешеходов, затем найти пройденное расстояние, к полученному результату прибавить расстоянием между населёнными пунктами.
4 + 5 = 9 (км/ч);
9 · 5 = 45 (км);
45 + 40 = 85 (км);
Ответ: Через 5 часов расстояние между пешеходами будет 85 км.

Задачи на движение в одном направлении

В таких задачах два объекта движутся в одном направлении с разной скоростью, при этом они сближаются друг с другом или отдаляются друг от друга. Соответственно находится скорость сближения или скорость удаления объектов.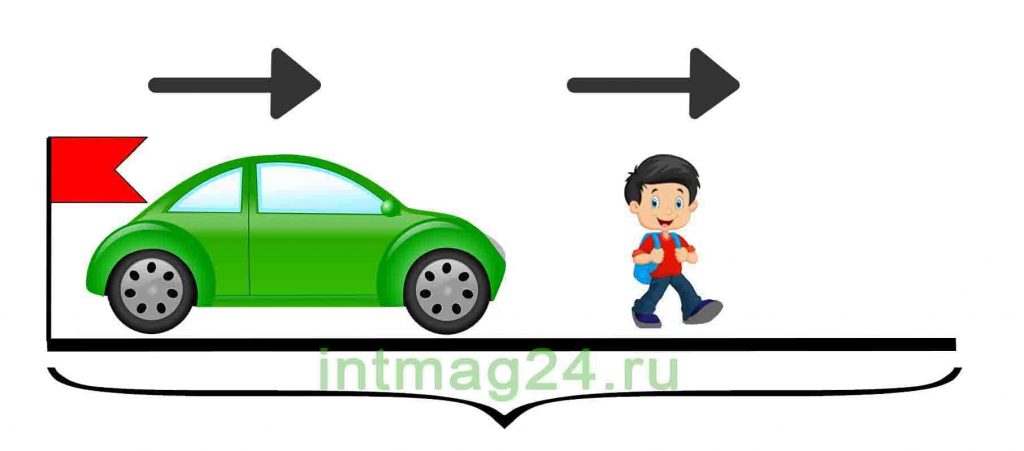

Формула нахождения скорости сближения или удаления двух объектов, которые движутся в одном направлении: из большей скорости вычесть меньшую.

Задача 8. 

Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?,
Решение: 
Задачу можно решить с помощью уравнения.
В этом случае скорость первого автомобиля 40 км/час, время в пути на 4 часа больше, чем время второго автомобиля (или t+4). Скорость второго автомобиля 60 км/час, время в пути – t. Расстояние оба автомобиля проехали одинаковое. Поэтому можно составить уравнение: 40*(t+4)=60*t. Отсюда получаем t=8 (часов) – время в пути второго автомобиля, за которое он догонит первый.
Решение задачи без использования уравнения.
Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалиться от города на: 40 · 4 = 160 (км).
Второй автомобиль движется быстрее первого, значит, каждый час расстояние между автомобилями будет сокращаться на разность их скоростей: 60 — 40 = 20 (км/ч) – это скорость сближения.
Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся: 160 : 20 = 8 (ч)
Ответ: Второй автомобиль догонит первый через 8 часов.

Задача 9. 

Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?
Решение: Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов: 5 — 4 = 1 (км/ч).
Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого: 5 : 1 = 5 (ч)
Ответ: Через 5 часов второй пешеход догонит первого.

Задача 10. 

Два автомобиля выехали одновременно из одного и того же пункта в одном направлении. Скорость первого автомобиля 80 км/ч, а скорость второго – 40 км/ч.
1) Чему равна скорость удаления между автомобилями?
2) Какое расстояние будет между автомобилями через 3 часа?
3) Через сколько часов расстояние между ними будет 200 км?
Решение: 
1) 80 — 40 = 40 (км/ч) — скорость удаления автомобилей друг от друга.
2) 40 · 3 = 120 (км) – расстояние между ними через 3 часа./
3) 200 : 40 = 5 (ч) – время, через которое расстояние между автомобилями станет 200 км.
Ответ:
1) Скорость удаления между автомобилями равна 40 км/ч.
2) Через 3 часа между автомобилями будет 120 км.
3) Через 5 часов между автомобилями будет расстояние в 200 км.

Задачи на движение по реке

Рассмотрим задачи, в которых речь идёт о движении объекта по реке. Скорость любого объекта в стоячей воде называют собственной скоростью этого объекта.

Чтобы узнать скорость объекта, который движется по течению реки, надо к собственной скорости объекта прибавить скорость течения реки. Чтобы узнать скорость объекта, который движется против течения реки, надо из собственной скорости объекта вычесть скорость течения реки.

Задача 11. 

Лодка движется по реке. За сколько часов она преодолеет расстояние 120 км, если ее собственная скорость 27 км/ч, а скорость течения реки 3 км/ч?
Решение: 
1) лодка движется по течению реки.
27 + 3 = 30 (км/ч) – скорость лодки по течению реки.
120 : 30 = 4 (ч) – проплывет путь.
2) лодка движется против течения реки.
27 — 3 = 24 (км/ч) — скорость лодки против течения реки
120 : 24 = 5 (ч) – проплывет путь.
Ответ:
1) При движении по течению реки лодка потратит 4 часа на путь.
2) При движении против течения реки лодка потратит 5 часов на путь.

Итак, для решения задач на движение:

1. Основная формула:S=ν*t;
2. Нужно сделать чертеж, который поможет определить тип задачи.
3. Все цифры нужно привести в единые единицы измерения: длина и время

Заключение.

Решая много задач по данной теме, ученик обязательно научится быстро ориентироваться в понятиях «скорость», «время» и «расстояние» и быстро решать задачи всех типов.

Весь курс начальной школы (за 1-4 классы) в краткой форме на сайте edu.intmag24.ru. С помощью курса можно быстро повторить основные моменты и правила по предметам: русский язык, математика, окружающий мир.

Для решения более сложных задач на движение посмотрите, как составлять схемы и таблицы данных для наглядного представления и структурирования данных.

772. Скорый поезд был задержан у семафора на 16 мин. и нагнал опоздание на перегоне в 80 км, идя со скоростью, на 10 км/час большей, чем полагалось по расписанию. Какова скорость поезда по расписанию? Решение Если же второй поезд отправится на 4 часа 20 минут раньше первого, то встреча произойдет через 8 часов после отправления первого. Если они будут продолжать путь, то, идя с прежней скоростью, первый придет в В через т часов, а второй придет в А через п часов после встречи.

Формула, которую обязательно нужно знать, и секрет, как ее легко запомнить

1. Вначале нам нужно внимательно прочитать условие задачи и определить, что же взять за переменную Х. Чаще всего в задачах на движение удобнее всего за переменную Х обозначить скорость. Если же скорость нам прямо дана в условиях задачи, то за переменную Х обозначаем время. Если в условиях задачи прямо указаны значения и скорости, и времени, тогда за переменную Х берем расстояние. Затем из условий задачи определить все, что нам известно и занести в таблицу.
2. На основании полученной таблицы составляем уравнение и решаем его. После решения уравнения не торопимся записывать ответ. Ведь нахождение Х – это не всегда ответ к исходной задаче. Такую ошибку совершают многие ученики: фактически правильно решив задачу, они записывают неправильный ответ.
3. После решения уравнения возвращаемся к условиям задачи и смотрим, что же требовалось найти. Находим неизвестное и записываем ответ.

Задачи на движение бывают разными. В таких задачах участники движения могут двигаться навстречу друг другу, вдогонку, они могут двигаться по реке (против течения или по течению). Каждая из этих задач имеет особенности решения, о которых мы поговорим ниже и разберем на примерах.

Сложная задача на логику — Журнал «Код» программирование без снобизма

786. По окружности длиной с равномерно и в одном направлении движутся две точки, которые сходятся через каждые t сек. Найти скорость каждой точки, зная, что одна из них пробегает всю окружность на п сек. быстрее другой. Решение По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых равны соответственно км ч и км ч. В таких задачах участники движения могут двигаться навстречу друг другу, вдогонку, они могут двигаться по реке против течения или по течению.

1. Если время движения сравнивается (то есть присутствуют слова больше/меньше), то мы приравниваем время и прибавляем слагаемое. То есть чтобы получить большее время, мы прибавляем к меньшему времени что-то еще (из условий задачи).
2. Если условия задачи содержат общее время, то дроби, выражающее время, складываются.

Данный случай предполагает, что в начальный момент времени движущиеся тела удалены друг от друга не некоторое расстояние S 0.
Из условий задачи известно, что автомобилист ехал на 3 часа дольше, чем мотоциклист (пользуемся первым правилом, которое разбирали при решении задач на движение вдогонку). Следовательно: Из условий задачи известно, что автомобилист ехал на 3 часа дольше, чем мотоциклист пользуемся первым правилом, которое разбирали при решении задач на движение вдогонку. Попробуем вычислить время, которое потребуется второму водителю, чтобы догнать первого, при условии, что они выехали в одно и то же время.

Комментарии

Кто сказал что длинна рельса 15 м. В условии задачи про это не сказано. Стандартная длина 12,5 25 и 50 м (ну это так к слову). И мы находясь в вагоне не знаем по какому участку в данный момент едем.
Так что ответ не верен .

Скорость можно узнать по «двойному стуку» двух колесных пар с блокированных в тележку. Растояние это не меняется во время движения, поэтому скорость равна L/T.
L — растояние между колесными парами.
Т — время между двумя ударами ( «стуками» ) колесных пар.

Допустим, количество толчков в минуту равно 50, это знчит, что за 1 мин. поезд проедит 50*15=750м=0,75км, т.е. за час получается 0,75*60=45км. По расчётам автора получается 9*50=450км/ч. Вывод: правильный ответ 0,9*[число толчков в минуту].

Прежде чем обсирать чужие решения, хорошенько подумайте, а не лоханетесь ли вы со своим ответом, когда к вам начнут также придираться ради стеба. В частности, хоть вы и отметили «двойной стук», но ваш ответ также не верен, ибо при прохождении стыков вагонов над стыками рельс раздается два двойных стука: «ту-дум—ту-дум».

а еще нужен секундомер, измерить точно время между стуками, или ноутбук с микрофоном и программой редактирования звуков. иначе точность будет никакой.
еще можно измерить при помощи GPS скорость, найти примерную длину рельса — округлить до стандартной длины рельса(не забыть прибавить зазор между рельсами), найти скорость:)

По-моему вопрос задан не корректно.
Можете ли вы определить скорость движения поезда по стуку колес?

Нет, я не могу определить скорость движения поезда по стуку колес. И чего дальше. мой ответ «нет» и он верен

Да чего Вы кипятитесь? Чувак пошутил — и молодец. А Вы так всё близко к сердцу приняли. И дело тут не в уме. Может у него секундомера нету или он глухой, или длину рельса не знает. Вот, я Вам дал «развёрнутое» объяснение.

А кто сказал, что скорость надо измерять в метрах в секунду или км в час?

Даже в россии уже давно рельсы сваривают дргу с другом, и стуков от езды по рельсам нет, а по другим стукам издаваемым колёсам нельзя!

Интересно,где это в России сваривают рельсы друг с другом? Наверное,после их сварки,рельсы перестают подчиняться законам физики(не сужаются и не расшираются).

Нет, рельсы после сварки не перестают подчиняться законам физики, но тем не менее их сваривают уже давно и находятся они в напряжении, которое в зависимости от периода года меняется. А не сварные рельсы применяются разве что на подъездных путях там где даже нет системы ключевой зависимости.

Метод ⭐ решения задач на движение: способы, схемы и планы решения задач

Классическая методика поиска решений заданий на движение включает такие пункты, как: Поскольку она развивает скорость 75 км ч, то до того момента, как столкнувшиеся локомотивы раздавят ее, муха успеет пролететь 150 км. В частности, хоть вы и отметили двойной стук , но ваш ответ также не верен, ибо при прохождении стыков вагонов над стыками рельс раздается два двойных стука ту-дум—ту-дум.
Время, которое тела провели в пути, удаляясь друг от друга, соответствует преодоленному расстоянию, поделенному на сумму скоростей этих тел.