Задача как найти ток короткого замыкания

Перейти к содержимому

Условие задачи:

Определить ток короткого замыкания источника питания, если при токе 15 А он отдает во внешнюю цепь мощность 135 Вт, а при токе 6 А – мощность 64,8 Вт.

Задача №7.4.36 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(I_1=15) А, (P_1=135) Вт, (I_2=6) А, (P_2=64,8) Вт, (I_{кз}-?)

Решение задачи:

Ток короткого замыкания (I_{кз}) определяют по формуле:

[{I_{кз}} = frac{{rm E}}{r};;;;(1)]

В этой формуле (rm E) – ЭДС источника питания, а (r) – его внутреннее сопротивление.

Запишем формулы для определения мощностей (P_1) и (P_2):

[left{ begin{gathered}
{P_1} = {U_1}{I_1} hfill \
{P_2} = {U_2}{I_2} hfill \
end{gathered} right.]

Напряжения на внешней цепи (U_1) и (U_2) можно найти по закону Ома для полной цепи:

[left{ begin{gathered}
{U_1} = {rm E} – {I_1}r hfill \
{U_2} = {rm E} – {I_2}r hfill \
end{gathered} right.]

Тогда:

[left{ begin{gathered}
{P_1} = left( {{rm E} – {I_1}r} right){I_1} hfill \
{P_2} = left( {{rm E} – {I_2}r} right){I_2} hfill \
end{gathered} right.]

Или, если раскрыть скобки в правой части:

[left{ begin{gathered}
{P_1} = {rm E}{I_1} – I_1^2r hfill \
{P_2} = {rm E}{I_2} – I_2^2r hfill \
end{gathered} right.]

Вот с этой системой нам и нужно будет поработать. Домножим обе части верхнего равенства на (I_2^2), а нижнего – на (I_1^2), тогда:

[left{ begin{gathered}
{P_1}I_2^2 = {rm E}{I_1}I_2^2 – I_1^2I_2^2r hfill \
{P_2}I_1^2 = {rm E}{I_2}I_1^2 – I_1^2I_2^2r hfill \
end{gathered} right.]

Вычтем из нижнего равенства верхнее:

[{P_2}I_1^2 – {P_1}I_2^2 = {rm E}{I_2}I_1^2 – {rm E}{I_1}I_2^2]

[{P_2}I_1^2 – {P_1}I_2^2 = {rm E}{I_1}{I_2}left( {{I_1} – {I_2}} right)]

Откуда ЭДС равна:

[{rm E} = frac{{{P_2}I_1^2 – {P_1}I_2^2}}{{{I_1}{I_2}left( {{I_1} – {I_2}} right)}};;;;(2)]

Возвращаемся опять к нашей системе (над которой мы хотели хорошо поработать). Домножим обе части верхнего равенства на (I_2), а нижнего – на (I_1), тогда:

[left{ begin{gathered}
{P_1}{I_2} = {rm E}{I_1}{I_2} – I_1^2{I_2}r hfill \
{P_2}{I_1} = {rm E}{I_1}{I_2} – I_2^2{I_1}r hfill \
end{gathered} right.]

Опять, вычтем из нижнего равенства верхнее:

[{P_2}{I_1} – {P_1}{I_2} = I_1^2{I_2}r – I_2^2{I_1}r]

[{P_2}{I_1} – {P_1}{I_2} = {I_1}{I_2}rleft( {{I_1} – {I_2}} right)]

Откуда внутреннее сопротивление равно:

[r = frac{{{P_2}{I_1} – {P_1}{I_2}}}{{{I_1}{I_2}left( {{I_1} – {I_2}} right)}};;;;(3)]

Подставим выражения (2) и (3) в формулу (1), тогда получим:

[{I_{кз}} = frac{{{P_2}I_1^2 – {P_1}I_2^2}}{{{P_2}{I_1} – {P_1}{I_2}}}]

Задача решена в общем виде, подставим данные задачи в полученную формулу и посчитаем ответ:

[{I_{кз}} = frac{{64,8 cdot {{15}^2} – 135 cdot {6^2}}}{{64,8 cdot 15 – 135 cdot 6}} = 60;А]

Ответ: 60 А.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

7.4.35 На сколько градусов поднимется температура медного стержня, если по нему в течение 0,5 с
7.4.37 ЭДС батареи аккумуляторов 12 В. Сила тока короткого замыкания 5 А. Какую наибольшую
7.4.38 В электрочайник с сопротивлением 140 Ом налита вода массой 1,5 кг при температуре 20 С

В сегодняшней статье разберем несколько решений задач на одну из распространенных тем: постоянный электрический ток.

Даже если задачи вас не интересуют, подписывайтесь на наш телеграм – там есть актуальные новости для студентов всех специальностей. А еще у нас есть канал, где можно найти приятные скидки на наши услуги.

Постоянный электрический ток: задачи

Рубрика «Физика для чайников» может пригодится вам в учебе. Там есть не только интересные статьи, но и решения задач по разным темам:

1. Закон Ома.
2. Параллельное и последовательное соединение проводников.
3. Правила Кирхгофа.
4. Работа и мощность тока.
5. Электрический ток в металлах.
6. Электрический ток в полупроводниках.
7. Ток в электиролитах и др.

Кстати, прежде чем приступать к решению задач по теме постоянный электрический ток, рекомендуем прочитать общую памятку: так у вас будет систематизированный план действий для решения любой задачи. На всякий случай под рукой можно держать полезные формулы.

Задача на постоянный ток №1

Условие

К источнику тока с ЭДС 1,5 В присоединили катушку с сопротивлением 0,1 Ом. Амперметр показал силу тока, равную 0,5 А. Когда к источнику тока присоединили последовательно еще один источник тока с такой же ЭДС, то сила тока в той же катушке оказалась равной 0,4 А. Определить внутренние сопротивления первого и второго источников тока.

Решение

Изобразим первоначальную схему:

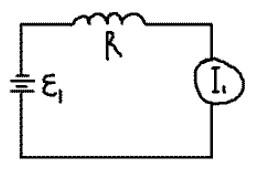
Общее сопротивление цепи:

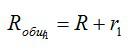
По закону Ома для участка цепи запишем:

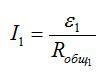
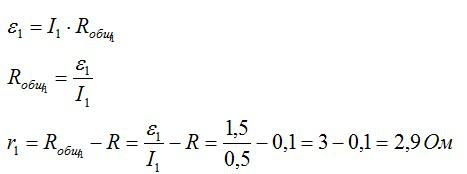
После последовательного подключения второго источника тока:

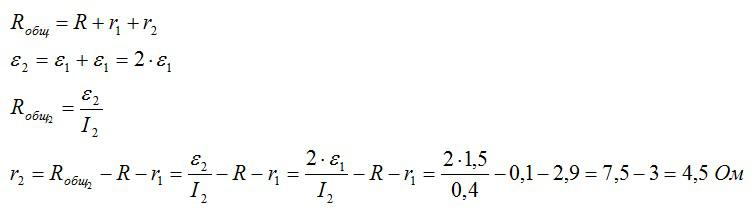Ответ: 2,9 Ом; 4,5 Ом

Задача на постоянный ток №2. Мощность тока

Условие

Два медных проводника одинаковой длины соединены последовательно и подключены к источнику тока, внутренним сопротивлением которого можно пренебречь.  При протекании тока в первом проводнике выделяется мощность P1. Какая мощность P2 выделяется в проводниках при их параллельном соединении, если площадь сечения второго проводника вдвое больше площади сечения первого проводника?

Решение

Запишем выражения для силы тока и мощности, выделяемой на проводниках, с учетом того, что проводники соединены последовательно:

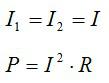
Сопротивление проводников равно:

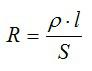
Теперь запишем выражения для мощности и выразим P2 через P1:

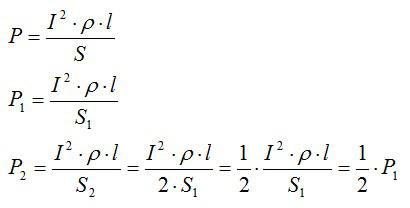
Ответ: P2 = 0,5P1

Задача на постоянный ток №3. Взаимодействие токов

Условие

Определите модуль силы, действующей на единицу длины второго проводника с током со стороны двух других проводников. Токи в проводниках равны I1=2А, I2=3А, I3=2А. Расстояние l=10 см.

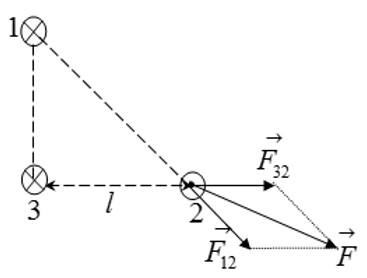
Решение

Направление силы показано на рисунке. 

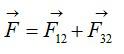
Силы 1-2 и 3-2 соответственно равны:

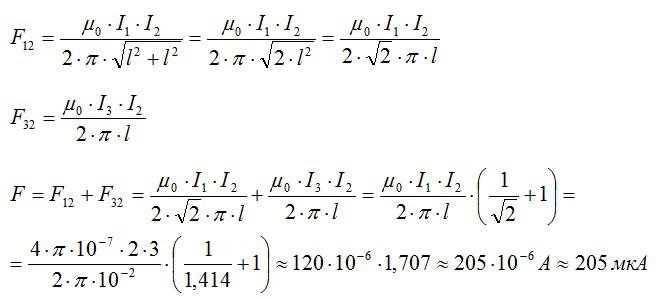
Ответ: 205 мкА.

Задача на постоянный ток №4. Короткое замыкание

Условие

Определить силу тока короткого замыкания в цепи, если при силе тока 2 А мощность тока во внешней цепи равна 10 Вт, а при силе тока 5 А мощность тока во внешней цепи равна 15Вт.

Решение

Чтобы вычислить ток короткого замыкания, нужно знать ЭДС и внутреннее сопротивление источника:

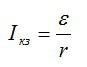
Запишем выражения для мощности тока во внешней цепи и напряжения нагрузки:

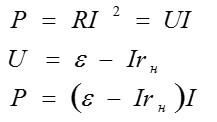
Условие задачи позволяет составить систему уравнений и найти нужные величины:

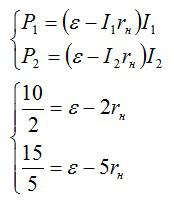
Отсюда: 

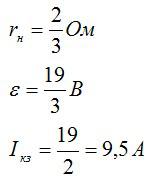
Ответ: 9,5 А.

Задача на постоянный ток №5. Закон Ома

Условие

Определить силу тока, проходящего через сопротивление 7 Ом, если напряжение на нем составляет 21 В.

Решение

Для решения этой элементарной задачи необходим закон Ома:

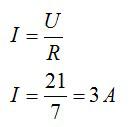
Ответ: 3 А.

Вопросы на тему «Постоянный ток»

Вопрос 1. Что такое электрический ток?

Ответ. Электрический ток – это упрядоченное движение заряженных частиц.

Вопрос 2. Какой ток называется постоянным?

Ответ. Постоянный ток – это ток, который со временем не меняется по величине и не меняет направления.

Ксати, в нашем блоге вы можете почитать о войне токов между Николой Теслой (переменный ток) и Томасом Эдисоном (постоянный ток).

Вопрос 3. Что определяет сила тока?

Ответ. Сила тока – это скаляр, который определяет заряд, переносимый через поперечное сечение проводника за определенное время.

Вопрос 4. Что такое ЭДС?

Ответ. ЭДС (электродвижущая сила) – скалярная физическая величина, равная отношению работы сторонних сил при перемещении заряда от отрицательного полюса источника тока к положительному, к величине этого заряда.

Вопрос 5. Как звучит закон Ома в простейщем виде?

Ответ. Закон Ома для участка цепи без ЭДС гласит:

Сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.

Нужна помощь в решении задач и выполнении других заданий? Обращайтесь в профессиональный студенческий сервис в любое время.