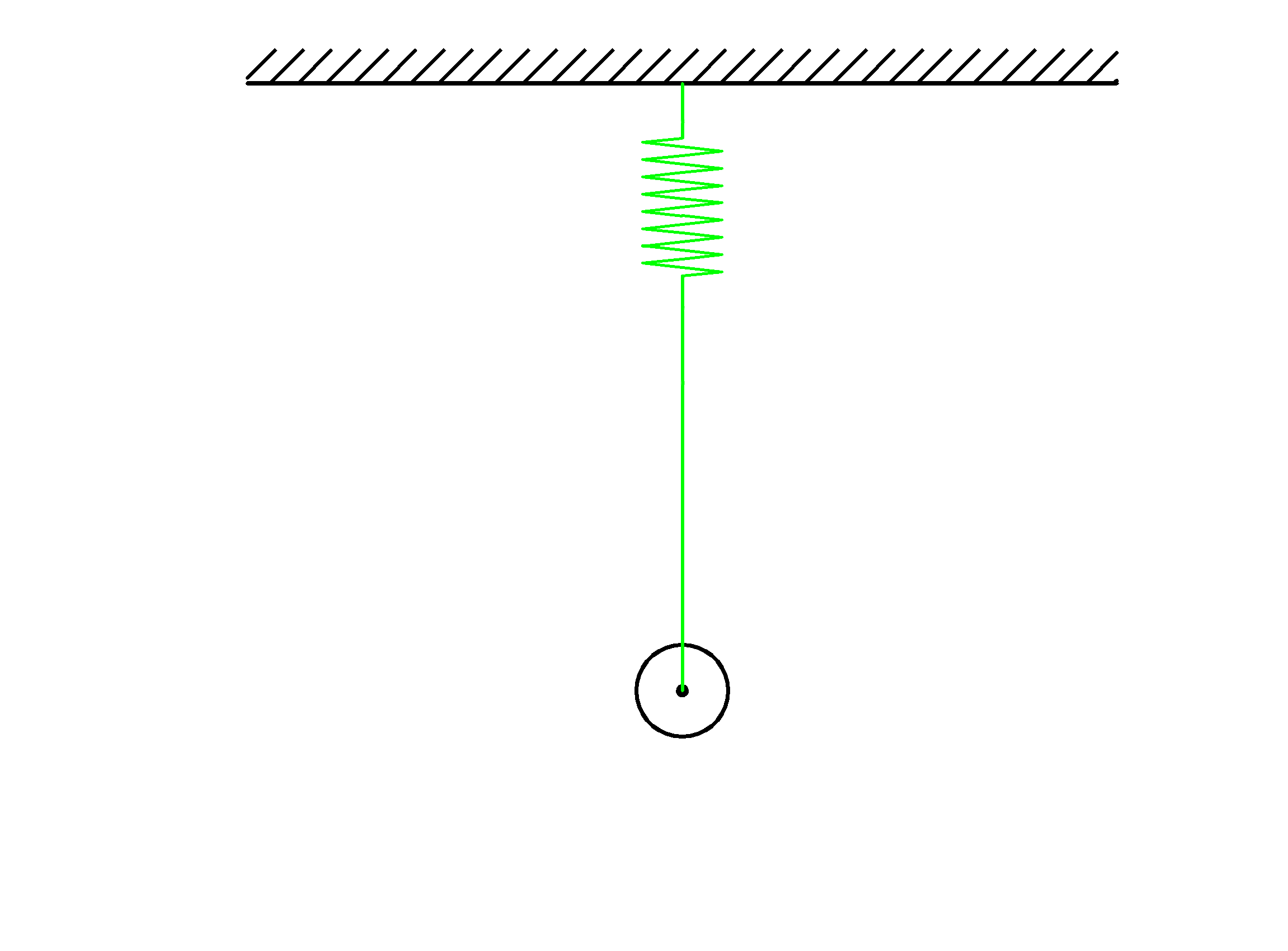
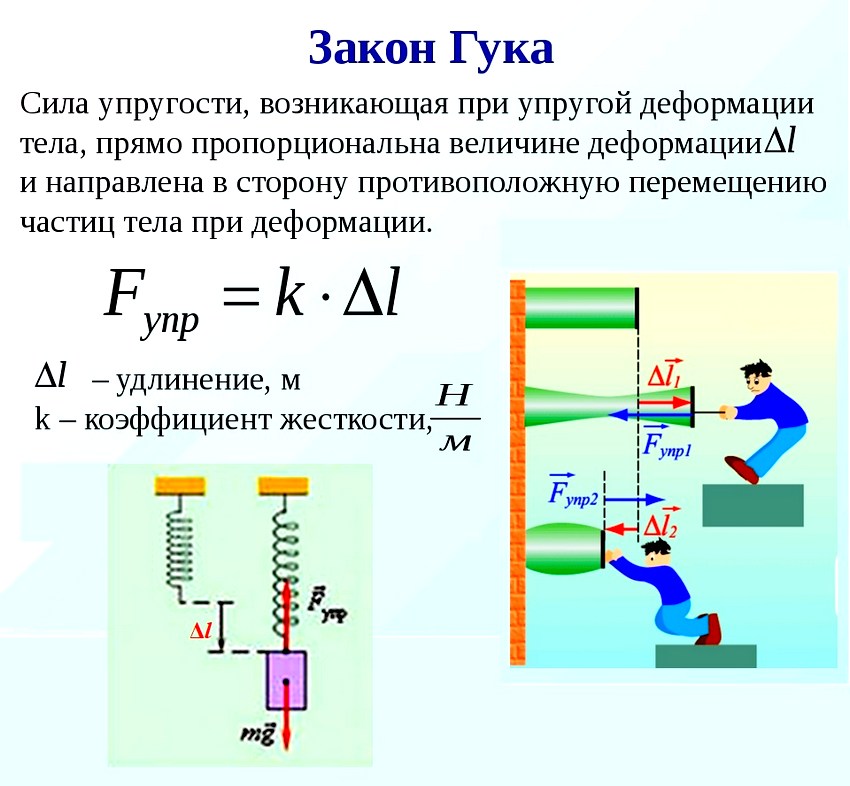
Задачи на закон Гука
(F=kx ) .
(F)- Сила, растягивающая или сжимающая пружину
(k)- коэффициент жесткости пружины
(x)- удлинение пружины (насколько растянулась пружина)
Репетитор по физике
+7 916 478 10 32
Задача 1. ( Закон Гука )
Пружина, с коэффициентом жесткости (k=100 Н/м ), растянулась на (x=0,1 м) после приложения к свободному концу
этой пружины силы (F.)
Найти силу (F), приложенную к этой пружине.
Показать ответ
Показать решение
Видеорешение
Задача 2. ( Закон Гука )
К пружине с коэффициентом жесткости (k=100 Н/м ) была приложена сила (F) , вследствии чего она удлиннилась на 10 сантиметров.
Найти силу (F), вызвавшую это удлинение.
Показать ответ
Показать решение
Видеорешение
Задача 3. ( Закон Гука )
Сила (F=50Н ) растягивает пружину на (x=0,5 м.)
Найти коэффициент жесткости этой пружины.
Показать ответ
Показать решение
Видеорешение
Задача 4. ( Закон Гука )
Найти коэффициент жесткости пружины, если сила (F=200Н), может растянуть эту пружину на 5 сантиметров.
Показать ответ
Показать решение
Видеорешение
Задача 5. ( Закон Гука )
На сколько растянется пружина с коэффициентом жесткости ( k=25Н/м ), если к ее будет растягивать сила
(F=10Н )
Показать ответ
Показать решение
Видеорешение
Задача 6. ( Закон Гука )
Найти растяжение пружины жесткостью ( k=600Н/м ), если к ее свободному концу приложить силу (F=30Н .)
Ответ дать в сантиметрах.
Показать ответ
Показать решение
Видеорешение
Задача 7. Приведено решение для тех, кому тяжело понять
Один конец пружины жесткостью ( k=400Н/м ) прикрепляют к потолку, а к другому ее концу
подвешивают груз массой (m=1 кг .)
На сколько сантиметров удлиннится пружина?
(g=10 Н/кг )
Показать ответ
Показать решение
Видеорешение
Задача 7. Приведено решение для тех, кто хочет научиться решать сложные задачи
Один конец пружины жесткостью ( k=400Н/м ) прикрепляют к потолку, а к другому ее концу
подвешивают груз массой (m=1 кг .)
На сколько сантиметров удлиннится пружина?
(g=10 Н/кг .)
Показать ответ
Показать решение
Видеорешение
Задача 8. Приведено решение для тех, кому тяжело понять
К свободному концу пружины жесткостью ( k=800Н/м ) прикрепляют груз массой (m=4 кг .)
Найти растяжение пружины.
Дать ответ в сантиметрах. (g=10 Н/кг . )
Показать ответ
Показать решение
Видеорешение
Задача 8. Приведено решение для тех, кто хочет научиться решать сложные задачи
Один конец пружины жесткостью ( k=800Н/м ) прикрепляют к потолку, а к другому ее концу
подвешивают груз массой (m=4 кг .)
На сколько сантиметров удлиннится пружина?
Дать ответ в сантиметрах. (g=10 Н/кг .)
Показать ответ
Показать решение
Видеорешение
Задача 9. Приведено решение для тех, кому тяжело понять
К пружине, закрепленной у потолка, подвешивают груз, при этом пружина растягивается на (x=0,08 м.)
Коэффициент жесткости пружины ( k=500Н/м ).
Найти массу груза, подвешенного к пружине.
(g=10 Н/кг . )
Показать ответ
Показать решение
Видеорешение
Задача 9. Приведено решение для тех, кто хочет научиться решать сложные задачи
К пружине, закрепленной у потолка, подвешивают груз, при этом пружина растягивается на (x=0,08 м.)
Коэффициент жесткости пружины ( k=500Н/м ).
Найти массу груза, подвешенного к пружине.
(g=10 Н/кг . )
Показать ответ
Показать решение
Видеорешение
Задача 10. Приведено решение для тех, кому тяжело понять
К пружине, закрепленной у потолка, подвешивают груз, при этом пружина растягивается на (x=0,01 м.)
Коэффициент жесткости пружины ( k=150Н/м ).
Найти массу груза, подвешенного к пружине.Дать ответ в граммах.
(g=10 Н/кг . )
Показать ответ
Показать решение
Видеорешение
Задача 10. Приведено решение для тех, кто хочет научиться решать сложные задачи
К пружине, закрепленной у потолка, подвешивают груз, при этом пружина растягивается на (x=0,08 м.)
Коэффициент жесткости пружины ( k=500Н/м ).
Найти массу груза, подвешенного к пружине. Дать ответ в граммах.
(g=10 Н/кг . )
Показать ответ
Показать решение
Видеорешение
Задача 11. ( Закон Гука )
Найти коэффициент жесткости пружины, если груз массой (m=5 кг ) растягивает ее на 2 сантиметра.
Показать ответ
Показать решение
Видеорешение
Задачи на силу упругости с решениями
Формулы, используемые на уроке «ЗАДАЧИ на силу упругости с решениями»
Название величины |
Обозначение |
Единицы измерения |
Формула |
Сила упругости |
Fупр |
H |
Fупр = –kx
|
Коэффициент упругости (жесткость) |
k |
H/м,кг/с2 |
k = ES/L |
Модуль Юнга (модуль упругости) |
E |
Н/м2 |
E = σ/ε |
Тренировочные задания для подготовки к контрольным, самостоятельным, проверочным и диагностическим работам.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Под действием груза в 200 Н пружина динамометра удлинилась на 0,5 см. Каково удлинение пружины под действием груза в 700 Н?
ОТВЕТ: 1,75 см.
Задача № 2.
Под действием силы давления вагона 50 кН буферные пружины между вагонами сжимаются на 1 см. С какой силой давит вагон, если пружины сжались на 4 см?
ОТВЕТ: 200 кН.
Задача № 3.
Резиновая лента удлинилась на 10 см под действием силы 10 Н. Какова ее жесткость?
ОТВЕТ: 100 Н/м.
Задача № 4.
Пружина без нагрузки длиной 20 см имеет коэффициент жесткости 20 Н/м. Какой станет длина пружины под действием силы 2 Н?
ОТВЕТ: на 0,1 м.
Задача № 5.
На сколько удлинится пружина под нагрузкой 12,5 Н, если под нагрузкой в 10 Н пружина удлинилась на 4 см?
ОТВЕТ: на 5 см.
Задачи на силу упругости
Задача № 6.
Какой груз нужно подвесить к пружине, жесткость которой 1000 Н/м, чтобы растянуть ее на 10 см?
ОТВЕТ: m ≈ 10 кг.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Задача № 7.
Грузовик взял на буксир легковой автомобиль «Волга» массой m = 2 т и, двигаясь равноускоренно, за 50 с проехал путь 400 м. На сколько удлинился при этом трос, соединяющий автомобили, если его жесткость 2 • 106 Н/м? Трением пренебречь.
ОТВЕТ: на 0,32 мм.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Задача № 8.
На рисунке приведен график зависимости удлинения резинового жгута от модуля приложенной к нему силы. Найти жесткость жгута.
ОТВЕТ: 10 Н/м.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Задача № 9.
Две пружины равной длины, скрепленные одними концами, растягивают за свободные концы руками. Пружина жесткостью 200 Н/м удлинилась на 4 см. Какова жесткость второй пружины, если ее удлинение равно 2 мм?
ОТВЕТ: 4000 Н/м.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Краткая теория к теме
«Задачи на силу упругости»
В физике упругость — это свойство твёрдых материалов возвращаться в свою первоначальную форму и размер после устранения сил, которые применялись при деформации. Виды упругих деформаций: растяжение, сжатие, кручение, изгиб, сдвиг, срез.
Силы упругости — силы, возникающие при деформации тела и направленные в сторону, противоположную деформации. При небольших деформациях растяжения или сжатия силу упругости можно определить по закону Гука: Fупр = –kx, где x — удлинение/сжатие тела (всегда положительное значение), k — коэффициент пропорциональности (коэффициент упругости), названный жесткостью тела Знак «минус» в законе означает, что сила упругости всегда направлена в сторону, противоположную деформации. Единицы измерения жесткости тела в СИ: 1 Н/м.
В некоторых учебниках и задачниках закон Гука выражают формулой Fупр = k • Δl. В этом случае: Δl — удлинение/сжатие тела (всегда отрицательное значение), k — коэффициент упругости (жесткость) тела.
Иногда, силу упругости, возникающую при деформации опоры, называют силой реакции опоры и обозначают буквой N. Силу упругости, возникающую при деформации нити или каната, называют силой натяжения нити (каната) и обозначают буквой Т.
Модуль Юнга (модуль упругости) — это физическая величина, которая характеризует свойства какого-либо материала сгибаться или растягиваться под воздействием силы; по сути именно от этого зависит жёсткость тела. Низкое значение модуля Юнга означает, что изучаемое твёрдое тело является эластичным. Высокое значение модуля Юнга означает, что изучаемое твёрдое тело является неэластичным или жёстким.
Конспект урока по физике «ЗАДАЧИ на силу упругости». Тренировочные задания для подготовки к контрольным, самостоятельным, проверочным и диагностическим работам. Выберите дальнейшее действие:
- Вернуться к Списку конспектов по физике для 7-11 классов
- Найти конспект через Кодификатор ОГЭ по физике
- Найти конспект через Кодификатор ЕГЭ по физике
В окружающем нас мире на различные тела действуют множество сил. Вы уже познакомились с несколькими из них: весом тела, силой тяжести и силой упругости.
- Сила тяжести действует на все тела находящиеся на Земле и всегда направлена вертикально вниз:
$F_{тяж} = gm$,
где $m$ — масса тела, $g$ — ускорение свободного падения ($g = 9.8 frac{Н}{кг}$) - Вес тела — это сила, с которой тело вследствие притяжения к Земле действует на опору или подвес. Вес тела приложен всегда к опоре или подвесу.
Если тело и опора/подвес неподвижны или движутся прямолинейно и равномерно, то вес будет численно равен силе тяжести, действующей на это тело:
$P = F_{тяж}$ - Сила упругости возникает в теле в результате его деформации и стремится вернуть тело в исходное положение.
Закон Гука определяет зависимость этой силы от деформации тела:
$F_{упр} = k Delta l$,
где $k$ — коэффициент упругости (жесткость тела), $Delta l$ — изменение длины тела
В данном уроке мы рассмотрим задачи и их подробные решения, чтобы вы научились уверенно использовать новые понятия и вычислять изученные силы.
Задача №1
Вычислите силу тяжести, действующую на тело массой: $1.5 space кг$; $500 space г$; $2.5 space т$; $20 space г$.
Дано:
$m_1 = 1.5 space кг$
$m_2 = 500 space г$
$m_3 = 2.5 space т$
$m_4 = 20 space г$
$g = 9.8 frac{Н}{кг}$
СИ:
$m_2 = 0.5 space кг$
$m_3 = 2500 space кг$
$m_4 = 0.02 space кг$
$F_{тяж1}, F_{тяж2}, F_{тяж3}, F_{тяж4} — ?$
Показать решение и ответ
Скрыть
Решение:
Сила тяжести рассчитывается по формуле $F_{тяж} = gm$.
Для того чтобы получить верный ответ при таких простых вычислениях, всегда обращайте внимание на единицы измерения данных величин. Мы уже перевели единицы массы в $кг$. Если бы мы этого не сделали, то получили бы неверные ответы.
Рассчитаем силу тяжести, действующую на каждое тело:
- $F_{тяж1} = gm_1$,
$F_{тяж1} = 9.8 frac{Н}{кг} cdot 1.5 space кг = 14.7 space Н$ - $F_{тяж2} = gm_2$,
$F_{тяж2} = 9.8 frac{Н}{кг} cdot 0.5 space кг = 4.9 space Н$ - $F_{тяж3} = gm_3$,
$F_{тяж3} = 9.8 frac{Н}{кг} cdot 2500 space кг = 24 space 500 space Н = 24.5 space кН$ - $F_{тяж4} = gm_4$,
$F_{тяж4} = 9.8 frac{Н}{кг} cdot 0.02 space кг = 0.196 space Н$
Ответ: $F_{тяж1} = 14.7 space Н$, $F_{тяж2} = 4.9 space Н$, $F_{тяж3} = 24.5 space кН$, $F_{тяж1} = 0.196 space Н$.
Задача №2
Банка объемом $5 space дм^3$ заполнена водой. Какой вес имеет вода?
Дано:
$V = 5 space дм^3$
$rho = 1000 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$
СИ:
$V = 5 cdot 10^{-3} space м^3$
Показать решение и ответ
Скрыть
Решение:
У нас в задаче не сказано, что банка каким-либо образом движется, поэтому мы будем считать, что она неподвижна. Если банка неподвижна, то и вода в ней тоже. Тогда вес воды мы можем рассчитать следующим способом:
$P = F_{тяж} = gm$.
Массу воды выразим через ее плотность и объем банки, который она заполняет:
$m = rho V$.
Подставим в нашу формулу и рассчитаем вес воды:
$P = g rho V$,
$P = 9.8 frac{Н}{кг} cdot 1000 frac{кг}{м^3} cdot 5 cdot 10^{-3} space м^3 = 49 space Н$.
Ответ: $P = 49 space Н$.
Задача №3
Два кубика изготовлены из одного материала. Объем первого кубика в 12.2 раза больше, чем второго. На какой кубик действует большая сила тяжести и во сколько раз?
Дано:
$V_1 = 12.2 V_2$
$rho_1 = rho_2 = rho$
$frac{F_{тяж1}}{F_{тяж2}} — ?$
Показать решение и ответ
Скрыть
Решение:
Сила тяжести рассчитывается по формуле:
$F_{тяж} = gm$.
Выразим массу кубиков через их объем и плотность:
$m_1 = rho V_1 = rho 12.2 V_2$,
$m_2 = rho V_2$.
Мы видим, что масса первого кубика в 12.2 раза больше массы второго. Это означает, что и сила тяжести, действующая на него, будет в 12.2 раза больше, чем сила тяжести, действующая на второй кубик:
$frac{F_{тяж1}}{F_{тяж2}} = frac{rho 12.2 V_2}{rho V_2} = 12.2$.
Ответ: на первый, в 12.2 раза.
Задача №4
Какой вес имеет человек, имеющий массу $65 space кг$ и находящийся на Земле?
Дано:
$m = 65 space кг$
$g = 9.8 frac{Н}{кг}$
$P — ?$
Показать решение и ответ
Скрыть
Решение:
Если человек находится на Земле неподвижно или движется равномерно и прямолинейно, то его вес будет равен силе тяжести, действующей на него:
$P = F_{тяж} = gm$,
$P = 9.8 frac{Н}{кг} cdot 65 space кг = 637 space Н$.
Ответ: $P = 637 space Н$.
Задача №5
Стальная проволока удлиняется на $2 space мм$ при действии на нее груза в $320 space Н$. Вычислите коэффициент жесткости проволоки.
Дано:
$Delta l = 2 space мм$
$F_{упр} = 320 space Н$
СИ:
$Delta l = 2 cdot 10^{-3} space м$
$k — ?$
Показать решение и ответ
Скрыть
Решение:
Запишем закон Гука:
$F_{упр} = k Delta l$.
Выразим отсюда коэффициент жесткости проволоки и рассчитаем его:
$k = frac{F_{упр}}{Delta l}$,
$k = frac{320 space Н}{2 cdot 10^{-3} space м} = 160 cdot 10^3 frac{Н}{м} = 160 frac{кН}{м}$.
Ответ: $k = 160 frac{кН}{м}$.
Задача №6
Под действием груза в $200 space Н$ пружина динамометра удлинилась на $0.5 space см$. Каково удлинение пружины под действием груза в $700 space Н$?
Дано:
$Delta l_1 = 0.5 space см$
$F_{упр1} = 200 space Н$
$F_{упр2} = 700 space Н$
$Delta l_2 — ?$
Показать решение и ответ
Скрыть
Решение:
Закон Гука описывает силу упругости, возникающую в пружине при ее удлинении:
$F_{упр1} = k Delta l_1$.
Выразим отсюда жесткость пружины и рассчитаем ее:
$k = frac{F_{упр1}}{Delta l_1}$,
$k = frac{200 space Н}{0.5 space см} = 400 frac{Н}{см}$.
Используя тот же закон Гука рассчитаем удлинение пружины при другой силе упругости, измерений динамометром:
$F_{упр2} = k Delta l_2$,
$Delta l_2 = frac{F_{упр2}}{k}$,
$Delta l_2 = frac{700 space Н}{400 frac{Н}{см}} = 1.75 space см$.
Ответ: $Delta l_2 = 1.75 space см$.
Под действием силы давления вагона $50 space кН$ буферные пружины между вагонами сжимаются на $1 space см$. С какой силой давит вагон, если пружины сжались на $4 space см$?
Дано:
$F_{упр1} = 50 space кН$
$Delta l_1 = 1 space см$
$Delta l_2 = 4 space см$
$F_{упр2} — ?$
Показать решение и ответ
Скрыть
Решение:
Вследствие давления вагона, буферные пружины сжимаются и в них возникает сила упругости, равная $50 space кН$. Найдем жесткость этих пружин:
$F_{упр1} = k Delta l_1$,
$k = frac{F_{упр1}}{Delta l_1}$,
$k = frac{50 space кН}{1 space см} = 50 frac{кН}{см}$.
Рассчитаем силу, с которой давит вагон, (силу упругости, возникающую в пружинах под таким давлением), если изменение длины пружин составило $4 space см$:
$F_{упр2} = k Delta l_2$,
$F_{упр2} = 50 frac{кН}{см} cdot 4 space см = 200 space кН$.
Ответ: $F_{упр2} = 200 space кН$.
Задача №8
Пружина без нагрузки длиной $20 space см$ имеет коэффициент жесткости $20 frac{Н}{м}$. Какой станет длина растянутой пружины под действием силы $2 space Н$?
Дано:
$l = 20 space см$
$k = 20 frac{Н}{м}$
$F_{упр1} = 2 space Н$
СИ:
$l = 0.2 space м$
$F_{упр2} — ?$
Показать решение и ответ
Скрыть
Решение:
Для того чтобы узнать длину растянутой пружины, нам нужно вычислить ее изменение длины — длину, на которую она растянется:
$l_1 = l + Delta l$.
Если бы пружина сжималась под действием силы, то мы бы отнимали удлинение от первоначальной длины.
Рассчитаем удлинение пружины:
$F_{упр} = k Delta l$,
$Delta l = frac{F_{упр}}{k}$,
$Delta l = frac{2 space Н}{20 frac{Н}{м}} = 0.1 space м$.
Теперь рассчитаем длину растянутой пружины:
$l_1 = 0.2 space м + 0.1 space м = 0.3 space м = 30 space см$.
Ответ: $l_1 = 30 space см$.
Задача №9
На рисунке 1 изображен график зависимости модуля силы упругости от удлинения пружины. Найдите жесткость пружины.
Показать решение и ответ
Скрыть
Решение:
Для того чтобы определить коэффициент жесткости нам нужно силу упругости разделить на удлинение пружины:
$k = frac{F_{упр}}{Delta l}$.
Пользуясь графиком, вы можете выбрать любую удобную для вас точку. График демонстрирует линейную зависимость силы упругости от удлинения, коэффициент жесткости при этом — величина постоянная.
Мы выберем точку, в которой сила упругости равна $4 space Н$. Этому значению силы соответствует удлинение пружины, равное $0.4 space м$.
Рассчитаем коэффициент жесткости:
$k = frac{4 space Н}{0.4 space м} = 10 frac{Н}{м}$.
Ответ: $k = 10 frac{Н}{м}$.
Задача №10
Круглый стальной брус диаметром $2 space см$, длиной $16 space м$ растягивается силой, равной $36 space кН$. Найдите удлинение этого бруса.
Дано:
$d = 2 space см$
$l = 16 space м$
$F_{упр} = 36 space кН$
$E = 200 cdot 10^9 space Па$
$Delta l — ?$
Модуль упругости $E$ — это физическая величина, характеризующая способность материала сопротивляться растяжению или сжатию.
Модуль упругости является характеристикой материала, для стали он равен $200 cdot 10^9 space Па$.
Он связан с коэффициентом упругости $k$:
$k = frac{ES}{l}$,
где $S$ — площадь поперечного сечения,
$l$ — длина.
Показать решение и ответ
Скрыть
Решение:
Запишем закон Гука:
$F_{упр} = k Delta l$.
Выразим отсюда удлинение стального бруса:
$Delta l = frac{F_{упр}}{k}$.
Коэффициент упругости $k$ мы можем выразить через модуль упругости $E$:
$k = frac{ES}{l}$.
Площадь поперечного сечения $S$ выразим через диаметр:
$S = frac{pi d^2}{4}$.
Подставим эти формулы в закон Гука:
$Delta l = frac{F_{упр}}{frac{ES}{l}} = frac{F_{упр} l}{E frac{pi d^2}{4}} = frac{4 F_{упр} l}{E pi d^2}$.
Рассчитаем удлинение бруса:
$Delta l = frac{4 cdot 36 cdot 10^3 space Н cdot 16 space м}{200 cdot 10^9 space Па cdot 3.14 cdot 0.02^2 space м^2} = frac{2304 cdot Н cdot м}{251 space 200 space Н} approx 0.009 space м approx 9 space мм$.
Ответ: $Delta l = 9 space мм$.
- Подробности
- Обновлено 02.09.2018 16:07
- Просмотров: 1663
Задачи по физике – это просто!
Вспомним
Изображение сил на чертеже:
Формула для расчета силы тяжести, действующей на тело:
Формула для расчета веса тела:
Форула для расчета силы упругости:
Здесь единица измерения массы – 1 кг,
единица измерения силы – 1 Н,
единица измерения жесткости пружины – 1 Н/м,
единица измерения величины деформации пружины (удлинения) – 1 м.
Все задачи решаем в системе СИ!
А теперь к задачам!
Элементарные задачи для 7 класса из курса школьной физики на расчет силы тяжести, веса тела и силы упругости.
Задача 1
Определить силу тяжести, действующую на тело массой 100 кг.
Задача 2
Определить вес тела массой 600 г.
Задача 3
Определить массу тела весом 120 Н.
Задача 4
На полу стоит ящик массой 1 тонна. Определить силу тяжести и силу упругости, действующие на ящик, а также вес ящика.
(Здесь N – сила реакции опоры, на которой стоит ящик, приложена к ящику, является силой упругости.
Если тело стоит неподвижно, т.е. не проваливается сквозь опору, то сила реакции опоры численно равна силе тяжести, действующей на тело.
Вес тела приложен к опоре и численно равен силе тяжести, действующей на тело.)
Задача 5
Определить вес алюминиевого бруска объемом 200 см3.
Задача 6
Определить силу упругости, возникающую при сжатии пружины на 10 см, если жесткость пружины равна 400 Н/м.
Задача 7
Определить максимальную силу упругости, возникающую при растяжении резины грузом массой 5 кг.
Задача 7
Найти удлинение пружины, возникающее под действием подвешенного к ней груза массой 200 г, если жесткость пружины равна 1000 Н/м.
(в этой задаче Х -это удлинение пружины, иначе величина деформации пружины, равна изменению длины пружины при деформации)
Сила упругости. Закон Гука
- Виды деформаций
- Закон Гука
- Измерение силы с помощью динамометра
- Задачи
п.1. Виды деформаций
Под действием силы все тело или отдельные его части приходят в движение.
При движении одних частей тела относительно других происходит изменение формы и размеров.
Деформация – это изменение взаимного положения частиц тела, связанное с их перемещением друг относительно друга под действием приложенной силы, при котором тело изменяет свою форму и размеры.
 |
К простейшим видам деформации относятся:
|
Различают упругие (обратимые) и неупругие (необратимые) деформации.
Деформация является упругой, если, после прекращения действия вызвавших её сил, тело полностью восстанавливает свою форму и размеры.
Например, если немного согнуть школьную линейку, растянуть пружину или надавить на воздушный шарик, после прекращения действия силы линейка выпрямится, пружина сожмется, и шарик опять станет круглым. Эти деформации – упругие, они обратимы.
Если же приложенная сила окажется слишком большой, линейка сломается, пружина так и останется растянутой, а шарик лопнет. Эти деформации – неупругие, они необратимы.
Все здания и сооружения вокруг нас рассчитываются так, чтобы их «нагруженные» части испытывали только упругие деформации; это обеспечивает надёжность и долговечность конструкций.
Восстановление формы и размера тела при упругой деформации происходит под действием силы упругости, которая возникает благодаря межатомным и межмолекулярным взаимодействиям.
Сила упругости уравновешивает действие внешней силы и направлена в сторону, противоположную смещению частиц.
Например (см. рисунок):
- при растяжении сила упругости стремится сжать тело;
- при сжатии сила упругости стремится распрямить тело.
п.2. Закон Гука
 |
Проведем серию опытов с пружиной. Пусть при действии на пружину силой (F) мы получаем деформацию (удлинение) (Delta l). При этом в пружине возникают силы упругости, стремящиеся вернуть её в исходное положение, (overrightarrow{F_{text{упр}}}=-overrightarrow{F}). Если приложенную силу увеличить в 2 раза, то деформация также увеличится в 2 раза. Увеличение силы в 3 раза приводит к росту деформации в 3 раза и т.д. Опыты показывают, что во всех случаях деформация будет прямо пропорциональна приложенной силе. |
Следовательно, сила упругости также будет прямо пропорциональна деформации: $$ F_{text{упр}}simDelta l $$
Для каждого тела отношение силы упругости к величине деформации при малых упругих деформациях является постоянной величиной $$ k=frac{F_{text{упр}}}{Delta l}=const $$ которая называется коэффициентом упругости или жесткостью.
Жесткость тела зависит от формы, размеров и материала, из которого оно изготовлено.
В системе СИ жесткость измеряется в ньютонах на метр, (frac{text{Н}}{text{м}}).
Закон Гука
Сила упругости, возникающая во время упругой деформации тела, прямо пропорциональна удлинению (величине деформации): $$ F_{text{упр}}=kDelta l $$ Сила упругости всегда направлена противоположно деформации.
п.3. Измерение силы с помощью динамометра
 |
Динамометр– это прибор для измерения силы.
Простейший пружинный динамометр состоит из пружины с крючком и дощечки со шкалой (проградуированной в ньютонах). |
В технике используются динамометры более сложных конструкций.
Но принцип действия – использование закона Гука – во многих из них сохраняется.
п.4. Задачи
Задача 1. Резиновая лента удлинилась на 10 см под действием силы 50 Н. Какова жесткость ленты?
Дано:
(Delta l=10 text{см}=0,1 text{м})
(F=50 text{Н})
__________________
(k-?)
Жесткость ленты $$ k=frac{F}{Delta l} $$ $$ k=frac{50}{0,1}=500 left(frac{text{Н}}{text{м}}right) $$ Ответ: 500 Н/м
Задача 2. Под действием силы 300 Н пружина динамометра удлинилась на 0,6 см. Каким будет удлинение пружины под действием силы 700 Н? Ответ запишите в миллиметрах.
Дано:
(F_1=300 text{Н})
(Delta l_1=0,6 text{см}=6cdot 10^{-3} text{м})
(F_2=700 text{Н})
__________________
(Delta l_2-?)
Жесткость пружины begin{gather*} k=frac{F_1}{Delta l_1}=frac{F_2}{Delta l_2}Rightarrow Delta l_2=frac{F_2}{F_1}Delta l_1\[6pt] Delta l_2=frac{700}{300}cdot 6cdot 10^{-3}=14cdot 10^{-3} (text{м})=14 (text{мм}) end{gather*} Ответ: 14 мм
Задача 3. Пружина без груза имеет длину 30 см и коэффициент жесткости 20 Н/м. Найдите длину растянутой пружины, если на нее действует сила 5 Н. Ответ запишите в сантиметрах.
Дано:
(l_0=30 text{cм}=0,3 text{м})
(k=20 text{Н/м})
(F=5 text{Н})
__________________
(l-?)
Удлинение пружины под действием силы: $$ Delta l=frac Fk $$ Длина растянутой пружины begin{gather*} l=l_0+Delta l=l_0+frac Fk\[6pt] l=0,3+frac{5}{20}=0,3+0,25=0,55 (text{м})=55 (text{cм}) end{gather*} Ответ: 55 cм
Задача 4*. Грузовик взял на буксир легковой автомобиль массой 1,5 т с помощью троса. Двигаясь равноускоренно, они проехали путь 600 м за 50 с. На сколько миллиметров удлинился во время движения трос, если его жесткость равна (3cdot 10^5 text{Н/м})?
Дано:
(m=1,5 text{т}=1500 text{кг})
(s=600 text{м})
(t=50 text{c})
(v_0=0)
(k=3cdot 10^5 text{Н/м})
__________________
(Delta l-?)
Сила упругости, возникающая в тросе, уравновешивает силу тяги, передвигающую автомобиль с постоянным ускорением: $$ F_{text{упр}}=kDelta l=F_{text{т}}=ma $$ Перемещение из состояния покоя $$ s=frac{at^2}{2}Rightarrow a=frac{2s}{t^2} $$ Получаем: begin{gather*} kDelta l=mcdotfrac{2s}{t^2}Rightarrow Delta l=frac mkcdot frac{2s}{t^2}\[6pt] Delta l=frac{1500}{3cdot 10^5}cdot frac{2cdot 600}{50^2}=2,4cdot 10^{-3} (text{м})=2,4 (text{мм}) end{gather*} Ответ: 2,4 мм