Задачи с процентами часто попадаются в экзаменационных заданиях. Многих они сбивают с толку – как разобраться с условием и как это решить? И совершенно зря, потому что с задачами на проценты каждый часто встречается в обычной жизни.
Пока такие задачки остаются оторванными от реальности строчками в учебнике, их бывает сложно понять и тем более решить. Чтобы стало понятнее, мы вам сейчас покажем примеры из обычной жизни, где вам могут встретиться проценты. А еще просто и доступно объясним, как решать задачи на проценты. И все у вас станет на свои места.
Задачи про проценты вокруг нас
Давайте оглядимся по сторонам: значения в процентах указаны на упаковках с любыми продуктами. Значок процента «%» смотрит на нас с рекламных плакатов скидок и распродаж. В новостях проценты сразу бросаются в глаза, когда речь идет о повышении цен на товары или коммунальные услуги. Разве вы сможете расшифровать все эти послания, если не научитесь решать задачи с процентами? Но вы, конечно, научитесь – мы в вас верим.
А вот такая ситуация: вы купили что-нибудь через интернет и получили извещение от ближайшего почтового отделения. Или сами собираетесь послать подарок другу в другой город. Вам обязательно надо уметь разбираться с процентами, чтобы узнать, сколько денег почта захочет получить за свои услуги по пересылке.
Или возьмем банковские кредиты и ипотеку. Банки в договорах всегда пишут мелкими буквами всякие вещи, которые полезно понимать. Например, какой процент по кредиту придется заплатить банку кроме тех денег, которые вы у него «одолжили» и обязаны вернуть.
А самый близкий школьникам пример связан с ЕГЭ. Каждый год после экзаменов публикуют официальную статистику. В которой немало задействованы и проценты. И эти проценты имеют прямое отношение к будущим выпускникам. Например, процент ребят, сдавших экзамен по математике на «хорошо» и «отлично» косвенно говорит о том, сколько абитуриентов с высокими баллами могли подать документы в вузы на технические специальности. А еще на программирование, прикладную математику и т.п. Чем их больше, тем выше конкурс. Если сравнивать их результаты со своими оценками, можно прикинуть собственные шансы на поступление.
Что такое процент?
Самое очевидное определение: процент – это десятичная дробь. В жизни редко что-то можно сравнивать целиком, чаще приходится сравнивать разные части чего-то целого. Поэтому мы используем такие понятия, как половина (1/2), треть (1/3), четверть (1/4). Ну да, все так привыкли к слову «четверть» в школе, что забывают о его формальном значении – «четвертая часть учебного года». Сравнивать сотые доли удобнее всего – так появился процент (1/100): pro centum – «за сто» на латыни.
Все задачи по математике на проценты вертятся вокруг сравнения частей одного целого, определения, какую долю составляет часть от целого, нахождения целого исходя из величины его части и т.п.
Проценты можно записать со знакомым всем значком процента: 1%. Можно представить в виде десятичной дроби (или натурального числа). Для этого нужно разделить на 100: 0,01. Можно наоборот: выразить число в процентах. Тогда его следует умножить на 100%.
Типы задач на проценты
Раз мы уже договорились, что задачи на проценты – это задачи на дроби, такой тактики будем придерживаться и дальше.
Тип 1: Находим процент (дробь) от числа.
- Задача. За месяц на предприятии изготовили 500 приборов. 20% изготовленных приборов не смогли пройти контроль качества. Сколько приборов не прошло контроль качества?
- Решение. Нужно найти 20% от общего количества изготовленных приборов (500). 20% = 0,2. 500 * 0,2 = 100. 100 из общего количества изготовленных приборов контроль не прошло.
Тип 2: Находим число по его проценту (дроби).
- Задача. Готовясь к экзамену, школьник решил 38 задач из пособия для самоподготовки. Что составляет 23% числа всех задач в пособии. Сколько всего задач собрано в этом пособии для самоподготовки?
- Решение. Мы не знаем, сколько всего задача в пособии. Но зато нам известно, что 38 задач составляют 25% от общего их количества. Запишем 23% в виде дроби: 0,23. Далее нам следует известную нам часть целого разделить на ту долю, которую она составляет от всего целого: 38/0,25 = 38 * 100/25 = 152. Именно 152 задачи включили в этот сборник.
Тип 3: Находим процентное отношение двух чисел (часть от целого числа).
- Задача. В классе 30 учеников. 14 из них – девочки. Сколько процентов девочек в классе?
- Решение. Чтобы узнать, какой процент составляет одно число от другого, нужно то число, которое требуется найти, разделить на общее количество и умножить на 100%. Значит, 14/30*100% = 7/15*100% = 7*100%/15 = 47%.
Тип 4: Увеличиваем число на процент.
- Задача. На прошлогоднем экзамене по математике 140 старшеклассников получили пятерки. В этом году число отличников выросло на 15%. Сколько человек получили пятерки за экзамен по математике в этом году?
- Решение. Если некое число а увеличено на х%, то оно увеличилось в (1 + х /100) раз. Откуда а * (1 + х /100). Подставим в эту формулу данные нам по условию задачи цифры и получим ответ: 140 * (1 + 15/100) = 161.
Тип 5: Уменьшаем число на процент.
- Задача. Год назад школу закончили 100 ребят. А в это году выпускников на 25 меньше. Сколько выпускников в этом году?
- Решение. Если число а уменьшено на х% и при этом 0 ≤ х ≤ 100, то число уменьшено в (1 – х/100) раз. И нужное нам число находим по формуле а * (1 – х/100). Подставляем цифры из условия задачи и получаем ответ: 100 * (1 – 25/100) = 75.
Тип 6: Задачи на простые проценты.
- Задача. Родители взяли в банке кредит 5000 рублей сроком на год под 15% ежемесячно. Сколько денег они заплатят банку через год?
- Решение. Простые проценты называются так, потому что они начисляются многократно, но всякий раз к исходной сумме. Если обозначить исходную сумму как а, сумму, которая наращивается, как S, процентную ставку как х% и количество периодов начисления процента как у, то формулу можно записать так: S = а * (1 + у * х/100). Теперь подставим сюда цифры из условия задачи и узнаем, сколько денег родители заплатят банку: S = 5000 * (1 + 12 * 15/100) = 14000.
Тип 7: Задачи на сложные проценты.
- Задача. На этот раз сумма кредита 25000 рублей, взятых под те же 15% сроком на 3 месяца. Снова надо узнать, сколько денег придется заплатить банку по истечении срока кредита.
- Решение. Сложные проценты отличаются от простых тем, что процент много раз начисляется не к исходной сумме, а к сумме с уже начисленными раньше процентами. Пускай снова S – наращиваемая сумма, а – исходная, х% – процентная ставка, у – количество периодов начисления процента. В этом случае формула принимает вид: S = а * (1 + х/100)у. Подставляем цифры из условия: S = 25000 * (1 + 15/100)3 = 38021,875 – искомая сумма.
Кстати, простые задачи на проценты можно очень легко решать с помощью пропорции. Этот метод наглядный и дает такой же результат, так что выбирать можно каждому тот способ решения, который кажется проще. Давайте решим задачу №3 про класс и процент девочек в нем, составив пропорцию.
- Решение. Обозначим искомый процент девочек в классе как х, общее количество учеников примем за 100%. Пропорция выглядит так:
30 – 100%
14 – х%
Перемножим крест накрест левую и правую части пропорции и получим, что 30* х = 14 * 100 («30 относится к х также, как 14 относится к 100»). Откуда найти х уже совсем несложно: х = 14 * 100/30 = 47%.
Задачи на проценты с решением
Давайте решим несколько задач для подготовки к ЕГЭ. Как вы сами видите, решать их совсем несложно. Сейчас просто закрепим материал.
Задача 1. После открытия торгов на бирже в понедельник акции некой компании выросли в цене на неизвестное количество процентов. А во вторник на то же самое количество процентов упали в цене. В итоге они подешевели на 4% по отношению к своей первоначальной стоимости в понедельник. На какой процент акции этой компании поднимались в цене в понедельник?
Решение. Пускай первоначальная стоимость акций это 1. В понедельник акции дорожают на х * 100%. Их стоимость в это время: 1 + х * 1. Во вторник акции дешевеют на х * 100%. Их стоимость после этого: 1 + х – х * (1 + х). После чего они стали дешевле на 4%, т.е. стали стоить 0,96.
Отсюда 1 + х – х * (1 + х) = 0,96 ↔1 – х2 = 0,96 ↔ х2 = 0,04 ↔ х = 0,2. Т.е. в понедельник акции компании дорожали на 20%.
Задача 2. Четыре пары брюк дешевле одного пальто на 8%. Подсчитайте, на сколько процентов пять пар брюк стоят дороже, чем одно пальто.
Решение. Исходя из условия задачи, стоимость четырех пар брюк – это 92% от стоимости пальто. Легко подсчитать, что стоимость одной пары брюк – это 23% стоимости пальто (92/4 = 23). Теперь умножим стоимость одной пары брюк на пять и узнаем, что пять пар брюк обойдутся в 115% стоимости пальто (23 * 5 = 115). Т.е. пять пар брюк на 15% дороже, чем одно пальто.
Задача 3. Семья состоит из трех человек: муж, жена и дочь-студентка. Если зарплата мужа вырастет в два раза, общий доход семьи возрастет на 67%. Если дочери в три раза урежут стипендию, общий доход этой семьи уменьшится на 4%. Надо вычислить, какой процент в общий доход семьи приносит заработок жены.
Решение. Из условия следует, что общий доход семьи находится в прямой зависимости от доходов мужа. Не так важно, насколько ему поднимут зарплату. В любом случае общий доход семьи вырастет на 67%. Значит, зарплата мужа составляет как раз эти 67% от общего дохода. Если стипендия дочери уменьшится в три раза (т.е. на 1/3), останется 2/3 – это и есть 4%, на которые уменьшился бы семейных доход. Можно составить простую пропорцию и выяснить, что раз 2/3 стипендии – это 4% дохода, то вся стипендия – это 6%. А теперь отнимем от всего дохода вклад мужа и дочери и узнаем, какой процент составляет заработок жены в общем доходе семьи: 100% – 67% – 6% = 27%.
Задача 4. В емкости находится 5 литров водного раствора с концентраций вещества, равной 12%. В емкость добавили еще 7 литров воды. Раствор какой концентрации (с каким процентным содержанием вещества) получился после этого?
Решение. Опишем концентрацию вещества в растворе такой формулой: С = Vвещества/ Vраствора * 100%. Изначально в растворе содержится 0,12 * 5 = 0,6 литра вещества. Когда были добавлены 7 литров воды, объем раствора в емкости увеличился. Но концентрация вещества понизилась (его объем остался неизменным). Подставим все известные нам цифры в формулу и получим ответ: 0,6/5 + 7 *100% = 0,6 /12 * 100% = 5%.
Задача 5. В свежих абрикосах 90% влаги, а в кураге, которая из них получается, только 5%. Сколько килограммов абрикосов нужно, чтобы получить 20 килограммов кураги?
Решение. Исходя из условия, в абрикосах 10% питательного вещества, а в кураге оно содержится в концентрированном виде – 95%. Поэтому в 20 килограммах кураги 20 * 0,95 = 19 кг питательного вещества. На вопрос задачи мы ответим, если разделим одинаковое количество питательного вещества, которое содержится в разных объемах свежих абрикосов и кураги, на его процентное содержание в абрикосах. Чтобы получить 20 килограммов кураги, нужно взять 19/0,1 = 190 килограммов свежих абрикосов.
Заключение
Сами видите, решать задачи на проценты не так уж сложно. Если усвоить основные правила и подключить воображение, вы сможете щелкать такие задачки как орешки.
Вы даже можете составить задачу на проценты сами по нашим образцам. Кстати, будет очень хорошо, если вы так и поступите. Можете оставить нам свои задачи в комментариях – пускай другие наши читатели решат ваши задачи. А вы сможете решить те, что придумают они. Чтобы задач для подготовки к экзаменам получилось больше, расскажите про эту статью своим друзьям в социальных сетях.
Вот увидите, задачи на проценты вам придется решать еще много раз даже после того, как вы закончите школу. Они встречаются в физике, химии, биологии. Да и в повседневной жизни умение решать их может не раз пригодится. Не бойтесь сложных задач – мы всегда поможем вам найти к ним ключ.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Рассказываем, как решать задачи на нахождение числа по его процентам. Приводим алгоритм решения. Задачи для самостоятельного решения.
Содержание
скрыть
1
Суть задач на нахождение числа по его процентам
2
Алгоритм решения задач
3
Способы решения задач
3.1
Примеры решения задачи
3.2
Задачи для самостоятельного решения
Суть задач на нахождение числа по его процентам
Задачи на нахождение числа по его процентам – это задачи на нахождение целого числа по его процентной части.
Алгоритм решения задач
Алгоритм решения задач на нахождение числа по его процентам:
- Выполняем краткую запись задачи;
- Определяем способ и решаем задачу;
- Выписываем полный ответ.
Определяем способ решения:

Способы решения задач
Примеры решения задачи
Базовые знания:
Задача 1. Найти число, 22 % которого составляют 44.
Краткая запись:
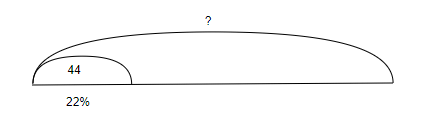
Решение:
1-й способ
- (44:22=2).
- (2⋅100=200).
2-й способ
- (22)%(=0,22).
- (44:0,22=4400:22=200).
Ответ: 200.
Задачи для самостоятельного решения
- В классе 16 девочек, что составляет 32 % числа всех учеников в классе. Сколько всего учащихся в классе?
- Найти число, если 9 % его составляют 72.
- Масса сушеных грибов составляет 12 % массы свежих. Сколько нужно взять свежих грибов, чтобы получить 3,6 кг сушеных?
- Сторона одного квадрата 4,8 см и составляет 12 % стороны другого квадрата. Найти площадь большего квадрата.
Посмотреть еще в категории: Задачи по математике 5-6 класс
- Задачи на сложение и вычитание
- Задачи на движение навстречу друг другу
- Задачи на движение в одном направлении
- Задачи на движение в противоположных направлениях
- Задачи на движение по реке
- Задачи на нахождение дроби от числа
- Задачи на нахождение числа по его дроби
- Задачи на нахождение процента от числа
- Задачи на процентное отношение двух чисел
- Задачи на проценты (с помощью пропорции)
- Задачи на нахождение градусной меры угла
- Задачи на нахождение периметра и площади треугольника
- Задачи с использованием формул площадей прямоугольника и квадрата
- Задачи на нахождение объема прямоугольного параллелепипеда и куба
- Задачи на проценты
- Задачи на нахождение длины окружности и площади круга
Летняя онлайн-школа, задание 8 июля для 6 класса. Повторим как решать задачи на нахождение числа по его процентам.
Чтобы найти число по данному его проценту нужно заменить проценты десятичной или обыкновенной дробью, исходя из того, что 1% = 0, 01 = 1/100, а затем разделить данное число на эту дробь.
Задание 8 июля для 6 класса
Реши задачи, ответы впиши вы форму и отправь на проверку.
- Сколько нужно взять пшеницы для получения 300 т муки, если при размоле пшеницы получается 80% муки?
- В первый день туристы преодолели 38,7 км, что составляет 14% всего пути. Сколько километров составляет весь намеченный путь?
форма для заполнения ответов
Как решать задачи на нахождение числа по его процентам
Задача 1
Тракторная бригада вспахала за день 25% всего поля, что составляет 60 га. Какова площадь всего поля ?
Решение:
Переводим проценты в десятичную дробь.
25% = 25 : 100 = 0, 25.
60 : 0,25 = 6000 : 25 = 240 (гектаров) — площадь всего поля.
Ответ: 240.
Задача 2
Цена на электрический чайник была повышена на 16% и составила 3480 рублей. Сколько рублей стоил чайник до повышения цены?
Цена чайника была повышена на 16% и стала в процентах составлять 116%. Так как 100% — это первоначальная цена чайника.
116% = 1,16.
3480 : 1,16 = 348000 : 116 = 3000 (рублей) — первоначальная стоимость чайника.
Ответ: 3000 рублей стоил чайник до повышения цены.
Задача 3
Налог на доходы составляет 13% от заработной платы. После удержания налога на доходы Мария Константиновна получила 9570 рублей. Сколько рублей составляет заработная плата Марии Константиновны?
Решение:
Полностью зарплата составляет 100%.
Подоходный налог — 13%.
После вычета налога: 100% — 13% = 87%.
87% = 0,87.
9570 : 0,87 = 957000 : 87 = 11000(руб) — заработная плата Марии Константиновны.
Ответ: 11000 рублей.
Вернуться к выбору заданий 6 класса
Задача. За контрольную по математике в пятом классе отметку «(5)» получили четверо учеников,
что составляет
16%
от всех учеников класса. Сколько учеников в классе?
I способ.
Найдём, какая часть всех учащихся класса приходится на
1%
:
Все ученики класса составляют целое:
100%
.
Умножим найденное число на (100):
Ответ: в классе (25) учеников.
Решение задачи можно записать по-другому.
В задаче надо найти такое число,
16%
которого равны (4).
Обозначим неизвестное число за (x), тогда получим равенство:
16%отxравно4;0,16отxравно4;0,16⋅x=4;x=4:0,16;x=400:16;x=25.
Ответ: в классе (25) учеников.
III способ.
Выразим проценты обыкновенной или десятичной дробью и
количество учеников, которые получили отметку «(5)», разделим на эту дробь:
,
или
Ответ: в классе (25) учеников.
Чтобы найти число по его проценту, надо:
1) выразить проценты обыкновенной или десятичной дробью;
2) разделить данное число на полученную дробь.
Решения задач на проценты
Ключевые слова конспекта: решения задач на проценты, ответы на типовые задачи, решения с пояснениями, математика для 5-6 классов; нахождение нескольких процентов от данной величины, восстановление величины по известным ее процентам, выражение отношения в процентах, увеличение (уменьшение) на несколько процентов, прикидка вместо точных подсчетов, увеличение (уменьшение) на несколько процентов раз и еще раз, сложные проценты, увеличение на 100%, 200%, уменьшение в несколько раз, проценты от процентов целого, нахождение целого по его процентам, выражение остатка процентами целого, выражение величины процентами целого, проценты от процентов целого, оставшиеся проценты целого, сложение процентов, уменьшение (увеличение) на несколько процентов, сравнение величин, отношение процентов, «потери», выраженные в процентах, концентрация раствора.
Задача № 1.
Нахождение нескольких процентов от данной величины.
В избирательном округе 35 000 избирателей. В голосовании приняло участие 67% всех избирателей. Сколько человек голосовало?
РЕШЕНИЕ:
Способ 1.
Сначала найдем 1% всего числа избирателей, т.е. одну сотую целого: 35 000 : 100 = 350. Теперь найдем 67% всего числа избирателей: 350 • 67 = 23 450.
Способ 2.
Используем умение находить часть целого. 67% величины – это 67 ее сотых долей, т.е. 67% выражаются дробью 67/100, или 0,67. Чтобы найти 67/100 (или 0,67), нужно 35 000 умножить на дробь: 35 000 • 0,67 = 23 450.
Ответ: 23 450 избирателей.
Задача № 2.
Восстановление величины по известным ее процентам.
В избирательном округе голосовало 23 450 избирателей, что составило 67% всех избирателей. Сколько всего избирателей в округе?
РЕШЕНИЕ:
Способ 1.
Сначала найдем 1% избирателей, принявших участие в голосовании: 23 450 : 67 = 350. Теперь найдем 100% всего числа избирателей: 350 • 100 = 35 000.
Способ 2.
Используем умение восстанавливать целое по известной его части.
67% величины – это 67 ее сотых долей, т.е. 67% выражаются дробью 67/100 или 0,67.
Чтобы найти 67/100 (или 0,67), нужно 23 450 разделить на дробь: 23 450 : 0,67 = 35 000.
Ответ: 35 000 избирателей.
Задача № 3.
Выражение отношения в процентах.
На телеграфе получено 360 телеграмм. Из них 144 телеграммы – поздравительные. Сколько процентов составляет часть поздравительных телеграмм?
РЕШЕНИЕ:
Сначала найдем, какую часть одна величина (число поздравительных телеграмм) составляет от другой (общего числа телеграмм): 144/360 = 2/5, затем выразим ее при необходимости десятичной дробью, а затем – и процентах 40%.
Ответ: 40%.
Задача № 4.
Увеличение (уменьшение) на несколько процентов.
Цена упаковки составляет 6% цены игрушки. Какова стоимость игрушки с упаковкой, если цена игрушки 650 р.?
РЕШЕНИЕ:
Способ 1.
Сначала найдем цену упаковки: 650 : 100 • 6 = 39 (р.). Теперь, увеличив цену, найдем стоимость игрушки с упаковкой: 650 + 39 = 689 (р.).
Способ 2.
Стоимость игрушки с упаковкой увеличилась на 6% и составила 100% + 6% = 106% цены игрушки. Так как 106% соответствует дроби 1,06 (или 106/100), то найдем 1,06 от 650. Имеем 650 • 1,06 = 689 (р.)
Ответ: 689 р.
Задача № 5.
Прикидка вместо точных подсчетов.
Примечание. Полезно знать некоторые факты. Так, чтобы увеличить целое на 50%, достаточно прибавить к нему половину; чтобы найти 20% величины, надо найти ее пятую часть; что треть величины – это примерно 33%. Кроме того, нередко в реальной жизни достаточно вместо точных подсчетов выполнить грубую прикидку.
Во время распродажи масляные краски для рисования стоимостью 213 р. за коробку продавали на 19% дешевле. Сколько примерно денег сэкономит художественная студия, если она купит партию в 150 коробок?
РЕШЕНИЕ:
213 р. – это примерно 200 р., 19% – это примерно 20%, т.е. пятая часть цены. Следовательно, коробка красок стоит на 200 : 5 = 40 р. дешевле, а 150 коробок на 40 • 150 = 6000 р. дешевле.
Ответ: примерно 6 тыс. р.
Задача № 6.
Увеличение (уменьшение) на несколько процентов раз и еще раз.
а) Зонт стоит 360 р. В ноябре цена зонта была снижена на 15%, а в декабре – еще на 10%. Какой стала стоимость зонта в декабре?
РЕШЕНИЕ:
Найдем стоимость зонта в ноябре: она составляет 85% от 360 р. Имеем: 360 • 0,85 = 306 (р.). Второе снижение цены происходило относительно новой цены зонта; теперь следует находить 90% от 306 р. Имеем: 306 • 0,9 = 275,4 (р.).
Ответ: 275 р. 40 к.
Дополнительный вопрос: на сколько процентов по отношению к первоначальной цене подешевел зонт?
Подсказка к решению. Найдите отношение последней цены к исходной, выразите его в процентах и сравните со 100%.
Ответ: зонт подешевел на 23,5%.
Задача № 7.
Сложные проценты.
а) Несколько лет тому назад в лесничестве росло 10 000 берез. Ежегодно подсаживали примерно 10% новых берез и в этом году насчитали примерно 13 300 берез. За сколько лет произошел такой прирост березовой рощи?
РЕШЕНИЕ:
Ежегодно число деревьев увеличивалось на 10%, т.е. в 1,1 раза, и составило в первый год 10 000 • 1,1 = 11 000, во второй 11 000 • 1,1 = 12 100, в третий 12 100 • 1,1 = 13 310 берез.
Ответ: за 3 года.
Задача № 8.
Увеличение на 100%, 200%.
Фирма в первый месяц выпустила 160 игрушечных автомобилей. В следующем месяце она увеличила выпуск этих игрушек на 200%. Во сколько раз увеличился выпуск игрушечных автомобилей? Сколько игрушечных автомобилей стала выпускать фирма?
РЕШЕНИЕ:
Исходный выпуск автомобилей составляет 100%, т.е. 160 автомобилей – это 100%. Тогда в следующем месяце выпуск автомобилей составил 100% + 200% = = 300%, т.е. в 3 раза больше. Значит, фирма стала выпускать 160 • 3 = 480 автомобилей.
Ответ: в 3 раза, 480 автомобилей.
Задача № 9.
Уменьшение в несколько раз.
Во сколько раз меньше стал стоить товар, если его уценили на 98% ?
РЕШЕНИЕ:
Стоимость товара 100%, а после его уценки на 98% стала 100% – 98% = 2%, т.е. уменьшилась в 100 : 2 = 50 раз.
Ответ: в 50 раз.
Задача № 10.
Проценты от процентов целого.
Из 550 учащихся школы в референдуме по вопросу о введении Ученического совета участвовали 88% всех учащихся. На вопрос референдума 75% учащихся, принявших участие в голосовании, ответили «да». Какой процент от числа всех учащихся школы составили те, которые ответили положительно?
РЕШЕНИЕ:
Способ 1.
Выразим проценты дробями и вычислим число учащихся, утвердительно ответивших на вопрос референдума. Имеем 550 • 0,88 • 0,75 = 363 (уч.). Теперь найдем ответ на вопрос задачи: 363 : 550 = 0,66 – это 66%.
Способ 2.
Выразим проценты дробями и перемножим дроби, т.е найдем 0,75 от 0,88 и получим 0,66 – это 66%.
Ответ: 66%.
Задача № 11.
Нахождение целого по его процентам.
Летом на дачу с детским садом выехали 180 детей. Известно, что 10% детей не поехали на дачу. Сколько всего детей в детском саду?
РЕШЕНИЕ:
Выразим в процентах число детей, которые поехали на дачу: 100% – 10% = 90% и продолжим решение.
Способ 1: если 90% – это 180 детей, то 10% в 9 раз меньше, т.е. 20 детей, а 100% – это 200 детей.
Способ 2: 180 детей составляют 90%, т.е. 0,9 всех детей, найдем целое по его части: 180 : 0,9 = 200.
Ответ: 200 детей.
Задача № 12.
Выражение остатка процентами целого.
Андрей за работу над новым проектом получил премию. Он истратил часть денег на подарки: 5% – родителям, 10% – жене, 7% – сыну и у него осталось 11 700 р. Какую сумму денег составила премия?
РЕШЕНИЕ:
Выразим в процентах количество денег, оставшихся от премии, и вычислим целое по его проценту.
100% – 5% – 10% – 7% = 78%.
11 700 : 78/100 = 15 000 (р)
Ответ: 15 тыс. р.
Задача № 13.
Выражение величины процентами целого.
Среди участников кросса 35% студенты, остальные – старшеклассники, причем их на 252 человека больше, чем студентов. Сколько спортсменов участвует в кроссе?
РЕШЕНИЕ:
Найдем, на сколько процентов больше старшеклассников, чем студентов: (100% – 35%) – 35% = 30%. Эти 30% составляют 252 человека. Имеем 252 : 0,3 = = 840 (чел.).
Ответ: 840 человек.
Задача № 14.
Проценты от процентов целого.
Четверть тиража новой газеты раскуплена в первый же день ее выпуска, причем 64% этой газеты продано в газетных киосках. Сколько процентов всего тиража продано в газетных киосках?
РЕШЕНИЕ:
Четверть тиража новой газеты составляют его 25%. Найдем 64% от 25%, получим 0,16, т.е. 16%.
Ответ: 16% тиража.
Задача № 15.
Оставшиеся проценты целого.
Автомобиль прошел 40% пути, а затем 30% оставшегося расстояния. Сколько процентов всего пути ему осталось пройти?
РЕШЕНИЕ:
Способ 1.
После того как автомобиль прошел 40% пути, ему осталось пройти еще 60% пути. Найдем 30%, т.е. 0,3 от 60%, получим 18%. Значит, всего автомобиль прошел 40% + 18% = 58% пути и ему осталось пройти 100% – 58% = 42% пути.
Способ 2.
После того как автомобиль прошел 40% пути, ему осталось пройти еще 60% пути. А когда он пройдет 30% оставшегося расстояния, то ему останется пройти 70% оставшегося расстояния. Найдем 70%, т.е. 0,7 от 60%, получим 42%.
Ответ: 42% пути. Проверьте ответ, считая путь равным конкретному числу, например, 100 км.
Задача № 16.
Сложение процентов.
В школе 16% девочек и 28% мальчиков занимаются в спортивных секциях. Сколько всего процентов школьников занимаются в спортивных секциях, если число мальчиков и число девочек в школе одинаково?
РЕШЕНИЕ:
Число мальчиков и девочек в школе одинаково, а значит, в школе 50% мальчиков и 50% девочек. Найдем 16%, т.е. 0,16 от 50%, получим 8%. Найдем 28%, т.е. 0,28 от 50%, получим 14%. Сложим проценты: 8% + 14% = 22% – столько процентов составляют учащиеся школы, которые занимаются в спортивных секциях.
Ответ: 22% школьников.
Задача № 17.
Уменьшение (увеличение) на несколько процентов.
На весенней распродаже в одном магазине товар уценили на 40%, а через неделю еще на 5%. На ярмарке тот же товар уценили сразу на 45%. Где выгоднее покупателю купить эту вещь?
РЕШЕНИЕ:
Товар выгоднее купить там, где он дешевле. В магазине после двух уценок цена товара составит 0,6 • 0,95 = 0,57 его первоначальной цены, а на ярмарке – 0,55 первоначальной цены. Так как 0,57 > 0,55, то правильный ответ: на ярмарке.
Ответ: на ярмарке.
Задача № 18.
Сравнение величин.
Во время распродажи кресло, стоившее 3000 р., продавали за 2400 р. На сколько процентов была снижена цена кресла на распродаже?
РЕШЕНИЕ:
Способ 1.
На сколько рублей новая цена меньше старой? На 600 р. На какую часть была снижена цена кресла? На 600/3000 = 1/5. На сколько процентов была снижена цена кресла? На 1/5 часть (на 2/10), т.е. на 20%.
Способ 2.
Какую часть новая цена составляет от старой? 2400/3000 = 8/10 = 0,8, т.е 80%. А это значит, что цена снижена на 20%.
Ответ: цена снижена на 20% .
Задача № 19.
Отношение процентов.
Отношение числа девочек в школе к числу мальчиков равно 4:5. Какую часть составляют девочки от числа всех учащихся школы? А мальчики? Выразите ответ в процентах.
РЕШЕНИЕ:
Если отношение числа девочек в школе к числу мальчиков равно 4:5, то число девочек составляет 4 части, а мальчиков 5 частей, а число всех учащихся школы – 9 таких же частей. Поэтому девочки от числа всех учащихся школы составляют 4/9, а мальчики 5/9.
Ответ: примерно 44% и 56%.
Задача № 20.
«Потери», выраженные в процентах.
При сушке яблоки теряют 75% своей массы, т.е. ту часть влаги, которая из нее выпаривается. Сушеные яблоки содержат 20% влаги. Какова влажность свежих яблок?
РЕШЕНИЕ:
Масса сушеных яблок составляет 100% – 75% = = 25% массы свежих яблок, и она содержит 0,25 • 0,2 = = 0,05, т.е. 5% влаги. Таким образом, влажность свежих яблок 75% + 5% = 80%.
Ответ: 80% массы.
Задача № 21.
Концентрация раствора.
Сколько граммов воды надо добавить к 180 г сиропа, содержащего 25% сахара, чтобы получить сироп, содержащий 20% сахара?
РЕШЕНИЕ:
Определим, сколько сахара в данной массе сиропа: 180 • 0,25 = 45 (г). Теперь найдем, сколько граммов 20–процентного сиропа получится, если взять 45 г сахара: 45 : 0,2 = 225 (г). Таким образом, в данную массу сиропа надо добавить 225 – 180 = 45 (г) воды.
Ответ: 45 г.
Это конспект по математике на тему «Решения задач на проценты». Выберите дальнейшие действия:
- Перейти к следующему конспекту:
- Вернуться к списку конспектов по Математике.
- Проверить знания по Математике.
