Задачи по физике как найти ускорение - Сайт, где вы сможете решить свои вопросы

ЗАДАЧИ на Прямолинейное равноускоренное
движение с решениями

Формулы, используемые в 9-11 классах по теме
«ЗАДАЧИ на Прямолинейное равноускоренное движение».

Название величины	Обозначение	Единица измерения	Формула
*Время*	t	с
*Проекция начальной скорости*	v_0x	м/с
*Проекция мгновенной скорости*	v_x	м/с
*Проекция ускорения*	a_x	м/с²
*Проекция перемещения*	S_x	м
*Координата*	x	м

1 мин = 60 с; 1 ч = 3600 с; 1 км = 1000 м; 1 м/с = 3,6 км/ч.

ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ

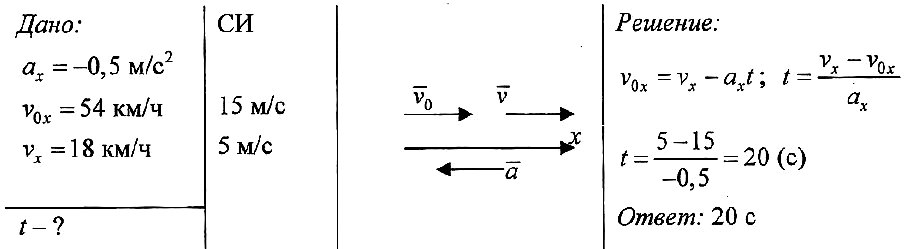
Задача № 1.
Автомобиль, двигаясь с ускорением –0,5 м/с², уменьшил свою скорость от 54 до 18 км/ч. Сколько времени ему для этого понадобилось?

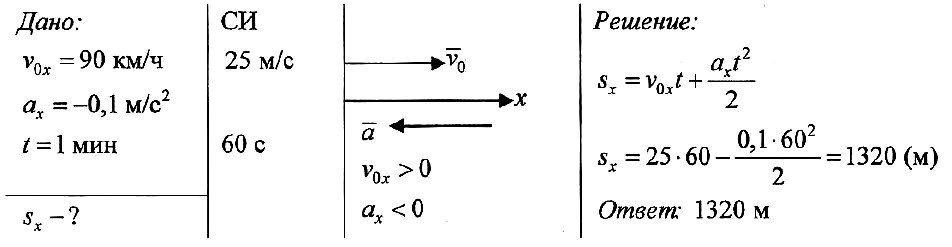
Задача № 2.
При подходе к станции поезд начал торможение с ускорением 0,1 м/с², имея начальную скорость 90 км/ч. Определите тормозной путь поезда, если торможение длилось 1 мин.

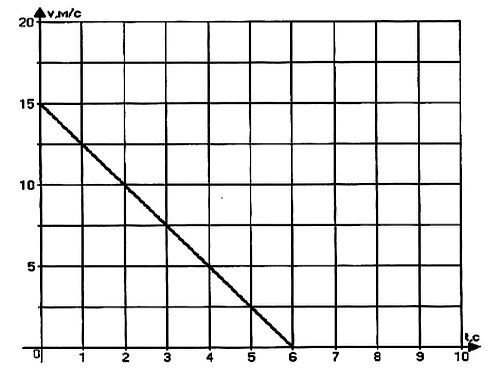
Задача № 3.
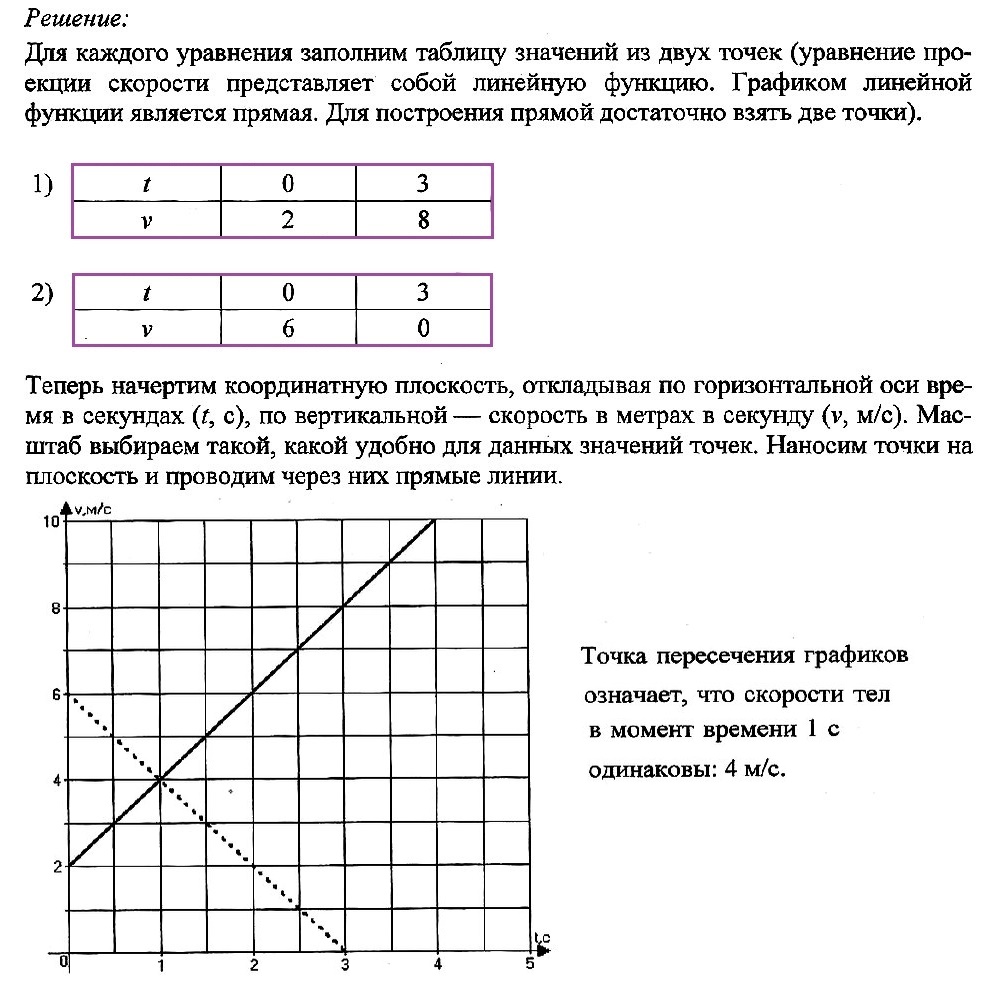
По графику проекции скорости определите: 1) начальную скорость тела; 2) время движения тела до остановки; 3) ускорение тела; 4) вид движения (разгоняется тело или тормозит); 5) запишите уравнение проекции скорости; 6) запишите уравнение координаты (начальную координату считайте равной нулю).

Решение:

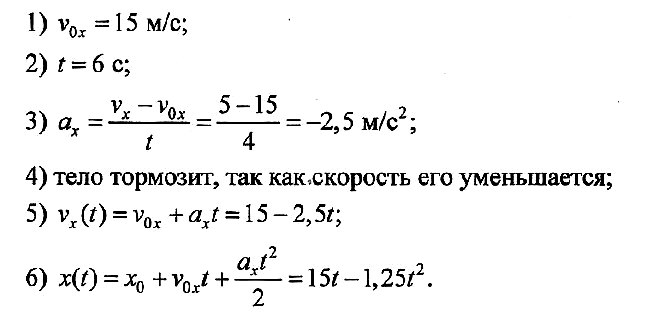
Задача № 4.
Движение двух тел задано уравнениями проекции скорости:
v_1x(t) = 2 + 2t
v₂_x(t) = 6 – 2t
В одной координатной плоскости постройте график проекции скорости каждого тела. Что означает точка пересечения графиков?

Задача № 5.
Движение тела задано уравнением x(t) = 5 + 10t — 0,5t². Определите: 1) начальную координату тела; 2) проекцию скорости тела; 3) проекцию ускорения; 4) вид движения (разгоняется тело или тормозит); 5) запишите уравнение проекции скорости; 6) определите значение координаты и скорости в момент времени t = 4 с. Сравним уравнение координаты в общем виде с данным уравнением и найдем искомые величины.

Решение:

Задача № 6.
Вагон движется равноускоренно с ускорением -0,5 м/с². Начальная скорость вагона равна 54 км/ч. Через сколько времени вагон остановится? Постройте график зависимости скорости от времени.

Задача № 7.
Самолет, летевший прямолинейно с постоянной скоростью 360 км/ч, стал двигаться с постоянным ускорением 9 м/с² в течение 10 с в том же направлении. Какой скорости достиг самолет и какое расстояние он пролетел за это время? Чему равна средняя скорость за время 10 с при ускоренном движении?

Задача № 8.
Трамвай двигался равномерно прямолинейно со скоростью 6 м/с, а в процессе торможения — равноускоренно с ускорением 0,6 м/с². Определите время торможения и тормозной путь трамвая. Постройте графики скорости v(t) и ускорения a(t).

Задача № 9.
Тело, имея некоторую начальную скорость, движется равноускоренно. За время t = 2 с тело прошло путь S = 18 м, причём его скорость увеличилась в 5 раз. Найти ускорение и начальную скорость тела.

Задача № 10. (повышенной сложности)
Прямолинейное движение описывается формулой х = –4 + 2t – t². Опишите движение, постройте для него графики v_x(t), s_x(t), l(t).

Задача № 11.
ОГЭ
Поезд, идущий со скоростью v₀ = 36 км/ч, начинает двигаться равноускоренно и проходит путь S = 600 м, имея в конце этого участка скорость v = 45 км/ч. Определить ускорение поезда а и время t его ускоренного движения.

Краткое пояснение для решения
ЗАДАЧИ на Прямолинейное равноускоренное движение.

Равноускоренным движением называется такое движение, при котором тело за равные промежутки времени изменяет свою скорость на одну и ту же величину. Движение, при котором скорость равномерно уменьшается, тоже считают равноускоренным (иногда его называют равнозамедленным).

Величины, участвующие в описании равноускоренного движения, почти все векторные. При решении задач формулы записывают обычно через проекции векторов на координатные оси. Если тело движется по горизонтали, ось обозначают буквой х, если по вертикали — буквой у.

Если векторы скорости и ускорения сонаправлены (их проекции имеют одинаковые знаки), тело разгоняется, т. е. его скорость увеличивается. Если же векторы скорости и ускорения противоположно направлены, тело тормозит.

Это конспект по теме «ЗАДАЧИ на Прямолинейное равноускоренное движение с решениями». Выберите дальнейшие действия:

Перейти к теме: ЗАДАЧИ на Свободное падение тел с решениями
Посмотреть конспект по теме КИНЕМАТИКА: вся теория для ОГЭ (шпаргалка)
Вернуться к списку конспектов по Физике.
Проверить свои знания по Физике (онлайн-тесты).

Источник

При решении задач на равноускоренное движение не обойтись без формул кинематики и второго закона Ньютона. Рекомендуем сначала изучить теорию по этим разделам, а уже потом приступать к практике.

Больше полезных сведений и ежедневная интересная рассылка – на нашем телеграм-канале, присоединяйтесь!

Равноускоренное движение: определение и примеры

Равноускоренное движение – это движение с меняющейся скоростью, но постоянным ускорением (a=const).

Самый простой случай такого движения – равноускоренное прямолинейное движение.

Вот типичные примеры равноускоренного движения:

рояль падает с 12-го этажа с ускоренинием свободного падения g;
автомобиль разгоняется со светофора от 0 до 60 км/ч с ускорением равным 1 метр на секунду в квадрате;
автобус плавно тормозит перед светофором. Это также равноускоренное движение, только векторы скорости и ускорения направлены в разные стороны.

Вопросы с ответами на равноускоренное движение

Вопрос 1. График движения представляет собой прямую линию. Является ли движение тела равноускоренным?

Ответ: да. Если график представляет собой кривую, то ускорение тела меняется со временем. Равномерное движение, которое также описывается прямой – частный случай равноускоренного движения с нулевым ускорением. Перемещение при равноускоренном движении численно равно площади трапеции, ограниченной осями координат и графиком.

Вопрос 2. Тело равномерно движется по окружности. Как направлено ускорение?

Ответ: перпендикулярно телу. В общем случае при криволинейном движении ускорение имеет две составляющие: нормальную (центростремительное ускорение) и тангенциальную, направленную по касательной к скорости. Тангенциальное ускорение при равномерном движении по окружности равно нулю.

Вопрос 3. Является ли ускорение свободного падения постоянным ускорением?

Ответ: да, является.

Вопрос 4. Может ли тело иметь нулевую скорость и ненулевое ускорение?

Ответ: да, может. После того, как скорость станет равна нулю, тело начнет двигаться в другом направлении.

Вопрос 5. Что такое ускорение?

Ответ: Векторная физическая величина, характеризующая изменение скорости за единицу времени. При равноускоренном движении скорость меняется одинаково за равные промежутки времени.

Задачи на равноускоренное движение

Сначала обратимся к уже приведенным примерам.

Задача №1. Равноускоренное движение

Условие

Рояль роняют с 12 этажа с нулевой начальной скоростью. За какое время он долетит до земли? Один этаж имеет высоту 3 метра, сопротивлением воздуха принебречь.

Решение

Известно, что рояль движется с ускорением свободного падения g. Применим формулу для пути из кинематики:

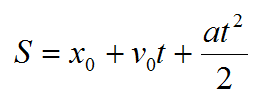
Начальная скорость равна нулю, а за точку отсчета примем то место, откуда рояль начал движение вниз.

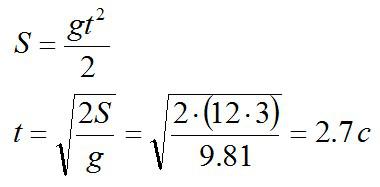
Ответ: 2.7 секунды.

Скорость свободно падающих тел не зависит от их массы. Любое тело в поле силы тяжести Земли будет падать с одинаковым ускорением. Этот факт был экспериментально установлен Галилео Галилеем в его знаменитых экспериментах со сбрасыванием предметов с Пизанской башни.

Задача №2. Равноускоренное движение

Условие

Автобус ехал со скоростью 60 км/ч и начал тормозить на светофоре с ускорением 0,5 метра на секунду в квадрате. Через сколько секунд его скорость станет равной 40 км/ч?

Решение

Вспоминаем формулу для скорости:

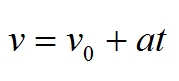
Начальная скорость дана в условии, но автобус тормозит, а значит, векторы скорости и ускорения направлены в противоположные стороны. В проекции на горизонтальную ось ускорение будем записывать со знаком минус:

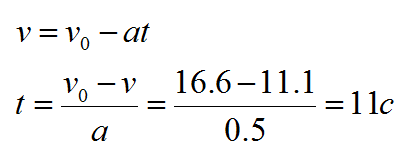
Ответ: 11 секунд.

Обязательно переводите величины в систему СИ.Чтобы перевести километры в час в метры в секунду нужно значение скорости в километрах в час сначала умножить на 1000, а потом разделить на 3600.

Задача №3. Нахождение ускорения

Условие

Тело движется по закону S(t)=3t+8t^2+2t. Каково ускорение тела?

Решение

Вспоминаем, что скорость – это производная пути по времени, а ускорение – производная скорости:

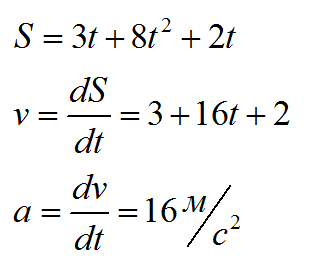
Ответ: 16 метров на секунду в квадрате.

При решении физических задач не обойтись без знания производной.

Кстати! Для всех наших читателей действует скидка 10% на любой вид работы.

Задача №4. Нахождение ускорения при равноускоренном движении

Условие

Грузовик разгоняется на дороге, а в кузове лежит незакрепленный груз. С каким максимальным ускорением должен разгоняться грузовик, чтобы груз не начал смещаться к заднему борту? Коэффициент трения груза о дно кузова k=0.2, g=10 м/c2

Решение

Для решения этой задачи нужно использовать второй закон Ньютона. Сила трения в данном случае равна F=kmg.

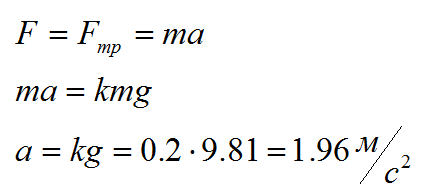
Ответ: 2 метра на секунду в квадрате.

Задача №5. Нахождение ускорения и скорости при равноускоренном движении

Условие

За пятую секунду прямолинейного движения с постоянным ускорением тело проходит путь 5 м и останавливается. Найти ускорение тела.

Решение

Конечная скорость тела v равна 0, v нулевое – скорость в конце 4-й секунды.

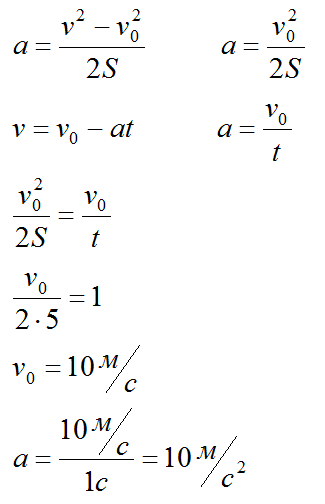
Ответ: 10 метров на секунду в квадрате.

Нужна помощь в решении задач? Обращайтесь в профессиональный студенческий сервис в любое время.

Источник

Уровень А

1. Куда направлены ускорения следующих тел:

а) у поезда, который начинает тормозить;

б) у поезда, который отходит от станции?

Решение

2. Куда движутся тела и как изменяются их скорости, векторы начальных скоростей и ускорений которых показаны на рисунке 1?

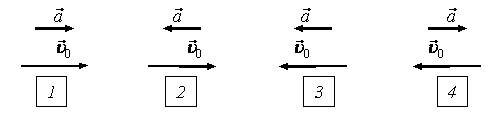
Рис. 1.

Решение

3. Скорость движения автомобиля за 40 с возросла от 5 м/с до 15 м/с. Определите ускорение автомобиля.

Решение

4. С каким ускорением двигался автобус, если, трогаясь с места стоянки, он развил скорость 15 м/с за 50 с?

Решение

5. Двигаясь со скоростью 72 км/ч, мотоциклист притормозил и через 20 с достиг скорости 36 км/ч. С каким ускорением он тормозил?

Решение

6. Поезд подходит к станции со скоростью 21,6 км/ч и останавливается через минуту после начала торможения. С каким ускорением двигался поезд?

Решение

7. В начале измерения скорость тела равнялась 5 м/с и направлена была на север. Через 50 с измерения показали, что тело двигается со скоростью 15 м/с на юг. Считая движения тела равноускоренным прямолинейным, определите его ускорение.

Решение

8. Троллейбус, трогаясь с места, движется с постоянным ускорением 1,5 м/с². Через сколько времени он приобретет скорость 54 км/ч?

Решение

9. Через сколько времени останавливается автобус, если его начальная скорость 20 м/с, а ускорение 1,25 м/с²?

Решение

10. Двигаясь с ускорением 5 м/с² скорость космической ракеты увеличилась на 100 м/с. За какое время произошло такое изменение скорости?

Решение

11. Какую скорость приобретает отходящий от станции поезд через 7 с от начала движения, если его ускорение равно 0,9 м/с²?

Решение

12. Какую скорость приобретает автомобиль при торможении с ускорением 0,5 м/с² через 10 с от начала торможения, если начальная скорость его была равна 72 км/ч?

Решение

13. Определите скорость тела при торможении с ускорением 0,2 м/с² через 30 с от начала торможения, если начальная скорость его была равна 2 м/с.

Решение

14. На каком расстоянии от Земли оказался бы космический корабль через 30 мин после старта, если бы он все время двигался с ускорением 9,8 м/с²?

Решение

15. Тело движется прямолинейно равнозамедленно с начальной скоростью 10 м/с и ускорением 2 м/с². Определите перемещение тела через 5 с после начала движения.

Решение

16. Чтобы оторваться от земли, самолет должен набрать скорость 180 м/с. На каком расстоянии от места старта на взлетной полосе самолет достигает этого значения скорости, если его ускорение постоянно и равно 2,5 м/с²?

Решение

17. Пассажирский поезд тормозит с ускорением 0,2 м/с². На каком расстоянии от места включения тормоза скорость поезда станет равной 5 м/с, если перед торможением скорость была 54 км/ч?

Решение

18. Автобус движется со скоростью 36 км/ч. На каком расстоянии от остановки водитель должен начать тормозить, сообщая автобусу ускорение, не превышающее 1,2 м/с²?

Решение

19. Автомобиль движется прямолинейно с постоянным ускорением 2,0 м/с², имея в данный момент скорость 10 м/с. Где он был 4,0 с назад?

Решение

20. Поезд, движущийся после начала торможения с ускорением 0,40 м/с², через 15 с имел скорость 10 м/с. Найдите пройденный путь за это время.

Решение

21. Снаряд, летящий со скоростью 1000 м/с, пробивает стенку блиндажа за 0,001 с, и после этого его скорость оказывается равной 200 м/с. Считая движение снаряда в толще стенки равноускоренным, найдите ее толщину.

Решение

22. После старта гоночный автомобиль достиг скорости 360 км/ч за 25 с. Какое расстояние он прошел за это время?

Решение

23. При аварийном торможении автомобиль, движущийся со скоростью 72 км/ч, остановился через 5 с. Найдите тормозной путь.

Решение

Уровень B

1. Шарик скатывается по желобу длиной 1,25 м с ускорением 1,6 м/с². Какова скорость шарика в конце жалоба?

Решение

2. Хоккейная шайба пересекла ледяное поле длиной 60 м за 3,0 с и остановилась. Какая скорость была сообщена шайбе клюшкой хоккеиста?

Решение

3. За какое время автомобиль, двигаясь из состояния покоя с ускорением 0,6 м/с², пройдет 30 м?

Решение

4. Самолет при отрыве от земли имеет скорость 252 км/ч и пробегает по бетонированной дорожке расстояние 700 м. Сколько времени продолжает разбег самолет? Движение считайте равноускоренным.

Решение

5. Ножной тормоз грузового автомобиля считается исправным если при торможении автомобиля, движущегося со скоростью 30 км/ч по сухой и ровной дороге, тормозной путь не превышает 9,0 м. Найдите соответствующее этой норме тормозное ускорение.

Решение

6. При какой начальной скорости поезд пройдет путь 1260 м в течении 60 с, замедляя ход с ускорением 1,5 м/с²?

Решение

7. Электропоезд тормозит с ускорением 0,40 м/с². Определите, за какое время он остановится, если тормозной путь равен 50 м.

Решение

8. Лифт Останкинской телевизионной башни заканчивает свое движение после прохождения 49 м за 14 с. Найдите ускорение и начальную скорость лифта.

Решение

9. Поезд, двигаясь с горы с ускорением 0,2 м/с², прошел путь 340 м и развил скорость 19 м/с. Сколько времени двигался поезд и какой была его скорость в начале отсчета?

Решение

10. Поезд, движущийся после начала торможения с ускорением 0,40 м/с², через 25 с остановился. Найдите скорость в момент начала торможения и тормозной путь.

Решение

Источник

Задачи на тему «Ускорение»

Задача 1.

Условие: самолет, летящий со скоростью 900 км/ч, совершает
посадку. Время до полной остановки самолета 25 с. Необходимо определить
длину взлетной полосы.

900 км/ч надо перевести в СИ, т.о. начальная скорость самолета
при посадке 250 м/с. Необходимо заметить, что, когда самолет совершает
посадку, его конечная скорость будет равна нулю.

На рисунке ускорение имеет направление против оси Ох,
тем самым мы должны понимать, что проекция ускорения на ось Ох будет
иметь отрицательное значение.

В данном случае движение прямолинейное (в одну сторону),
поэтому перемещение или
длина перемещения будет равна пройденному пути и определяется следующим
образом: .

Чтобы решить окончательно эту задачу, надо определить ускорение:

Обратите внимание, что ускорение получилось со знаком
минус. В данном случае мы понимаем, что движение замедленное. Скорость
с течением времени уменьшается.

Хотелось бы сделать акцент на том, что в решении мы не использовали
обозначение векторов. Вспомните, в начале рассуждения мы уже нарисовали
рисунок, где точно поставили направление векторных величин, связанных
с выбранной системой отсчета, т.е. с осью Ох. Подставляем в формулу,
в уравнение движения Галилея все нам известные
величины: .

Ответ: S = 3125 [м].

Задача на комбинацию различных видов
движения

Условие: автобус начинает свое движение от остановки и
за 5 с увеличивает свою скорость до 36 км/ч. Затем 20 с автобус едет с
постоянной скоростью и перед светофором тормозит, останавливается,
до полной остановки движется в течение 10 с. Определите полный пройденный
путь этим автобусом.

Решение задачи мы начинаем с того, что определим первый
участок пути, т.е. тот участок, на котором автобус разгоняется. Обозначим
его как S₁, и вычислять мы будем его по уравнению
Галилея. Записывается оно следующим образом: 1) .

Чтобы вычислить S₁,
требуется обязательно знать ускорение. Ускорение обозначим а = а₁.

Движение начинается от остановки, это означает, что начальная
скорость V₀ = 0.
Найдем ускорение: . Принимая, что V₀ =
0, формула приобретает вид =.

Отсюда следует, что == после
того, как мы подставим все значения.

Вычисляем теперь пройденный путь S₁.
С учетом того, что V₀ =
0, формула приобретает вид: .

Если теперь подставить сюда все известные значения, то мы
получаем значение: =.

Итак, первый этап: автобус разогнался от 0 до 10 м/с, пройдя
расстояние 25 м.

Следующая часть посвящена равномерному движению,
когда автобус движется равномерно в течение 20 с, и замедленному
движению, когда автобус начинает останавливаться. Определяем пройденное
расстояние при равномерном прямолинейном
движении. В этом случае S₂=
V₁^.t₂=
10^.20 = 200 [м].

Третий пункт – это момент остановки автобуса, т.е. расстояние,
которое он проходит до остановки. Здесь .

В этом уравнении, чтобы определить S₃,
требуется знать значение ускорения:

Это означает, что движение замедляется. Оно направлено
против выбранной оси. Подставив все значения, мы получаем выражение
для S₃: .

До полной остановки автобус проходит 50 м. Чтобы вычислить
окончательный ответ, нужно все пройденные расстояния сложить:

S = S₁+ S₂+
S₃= 25 + 200 + 50 = 275 [м].

Решение второй задачи графическим
методом

Рассмотрим второй вид решения, так называемый графический
способ решения. Вспомним, что площадь фигуры, ограниченная с одной
стороны осью времени, а с другой стороны графиком скорости, есть
пройденный путь.

Нарисуем график зависимости скорости автобуса от
времени. В течение 5 с скорость тела, скорость автобуса увеличивается
от 0 до 10 м/с. Затем 20 с, т.е. от 5 до 25 с, скорость постоянна и равна
10 м/с. Затем в течение 10 с, т.е. от 25 с до 35 с, автобус останавливается.

Рис. 3. График зависимости
скорости

от времени (задача 2)

Фигура, которая получается в связи с тем, что мы нарисовали,
– это трапеция. Из математики вы помните, что площадь трапеции определяется
как полусумма оснований, умноженная на высоту. Это .
В нашем случае =275
[м].

20 – это одно основание, верхнее основание, малое основание,
если хотите, то самое, которое определяется равномерным
движением автобуса и плюс 35.

Обратите внимание на ответ, который мы получили в первом
случае: S = S₁+
S₂+
S₃=
25 + 200 + 50 = 275 [м]. И ответ, который получили сейчас 275 [м].

Они одинаковы,
следовательно, решение задачи может быть и таким – аналитическим, и
графическим.

Источник

Из кодификатора по физике, 2020:

«1.1.6. Равноускоренное прямолинейное движение:

$x(t)={ x }_{ 0 }+{ upsilon }_{ 0x }cdot t+frac { { a }_{ x }cdot { t }^{ 2 } }{ 2 }$ , ${ upsilon }_{ x }(t)={ upsilon }_{ 0x }+{ a }_{ x }cdot t$
${ a }_{ x }=const$ , $quad { upsilon }_{ 2x }^{ 2 }-{ { upsilon } }_{ 1x }^{ 2 }=2{ a }_{ x }cdot ({ x }_{ 2 }-{ x }_{ 1 })$ .»

Теория

В данной статье будем считать, что Вы умеете без проблем находить проекции величин и в примерах не будем подробно объяснять, чему они равны.
В задачах на равноускоренное движение применяют пять величин: проекции перемещения ${ s }_{ x }$ , проекции начальной скорости ${ upsilon }_{ 0x }$ , проекции конечной скорости ${ upsilon }_{ x }$ , проекции ускорения ${ a }_{ x }$ и времени t. Достаточно знать любые три величины, чтобы найти все остальные.

При решении задач по данной теме применяют два способа решения.

1 способ. При решении запоминаем и применяем две формулы:

${ upsilon }_{ x }={ upsilon }_{ 0x }+{ a }_{ x }cdot t$ ,

${ s }_{ x }={ upsilon }_{ 0x }cdot t+frac { { a }_{ x }cdot { t }^{ 2 } }{ 2 }$ .

А в наиболее сложных случаях решаем систему этих двух уравнений.

2 способ. При решении запоминаем и применяем пять формул (см. таблицу 1).

Таблица 1

Почему пять формул? Каждая из этих формул использует только четыре величины из пяти. Одна из величин не используется при решении (отсутствует) (см. таблицу 1, столбец № 3). Вариантов с одной отсутствующей величиной из пяти может быть только пять.

Алгоритм решения вторым способом.

1) определите, какие величины используются (даны или надо найти), а ка-кая отсутствует;

2) по отсутствующей величину из таблицы выберите рабочую формулу.

Пример 1. Найдите перемещение ${ s }_{ x }$ , если известны ${ upsilon }_{ x }$ , ${ upsilon }_{ 0x }$ и ${ a }_{ x }$ .

Отсутствующая величина t. Согласно таблице 1 для решения нужно ис-пользовать формулу № 4:
${ s }_{ x }=frac { { upsilon }_{ x }^{ 2 }-{ upsilon }_{ 0x }^{ 2 } }{ 2{ a }_{ x } }$ .

Пример 2. Найдите перемещение ${ s }_{ x }$ если известны ${ upsilon }_{ x }$ , ${ upsilon }_{ 0x }$ и t.

Отсутствующая величина ${ a }_{ x }$ . Согласно таблице 1 для решения нужно использовать формулу № 5

${ s }_{ x }=frac { { upsilon }_{ x }+{ upsilon }_{ 0x } }{ 2 } cdot t$ .

Для сомневающихся и любопытных.

Вывод формулы №3. Из уравнения ${ upsilon }_{ x }={ upsilon }_{ 0x }+{ a }_{ x }cdot t$ найдем проекцию начальной скорости:

${ upsilon }_{ 0x }={ upsilon }_{ x }-{ a }_{ x }cdot t$ .

Подставим полученное выражение в формулу № 2:

Вывод формулы №4. Из уравнения ${ upsilon }_{ x }={ upsilon }_{ 0x }+{ a }_{ x }cdot t$ найдем время:

$t=frac { { upsilon }_{ x }-{ upsilon }_{ 0x } }{ { a }_{ x } }$ .

Подставим полученное выражение в формулу № 2:

Вывод формулы №5. Из уравнения ${ upsilon }_{ x }={ upsilon }_{ 0x }+{ a }_{ x }cdot t$ найдем проекцию ускорения:

${ a }_{ x }=frac { { upsilon }_{ x }-{ upsilon }_{ 0x } }{ t }$ .

Подставим полученное выражение в формулу № 2:

Задачи

Задача 1. Пассажирский поезд тормозит с ускорением 0,2 м/с2. На каком расстоянии от места включения тормоза скорость поезда станет равной 5 м/с, если перед торможением скорость была 15 м/с?

Решение. Скорость поезда уменьшается, поэтому ускорение направлено против начальной скорости. При прямолинейном движении (без поворотов) перемещение поезда равно расстоянию, которое он пройдет, т.е. s = s. Ось 0Х направим по направлению начальной скорости (рис. 1), поэтому

${ s }_{ x }=s,quad { upsilon }_{ x }=upsilon ,quad { upsilon }_{ 0x }={ upsilon }_{ 0 },quad { a }_{ x }=-a$

1 Способ. Из уравнения ${ upsilon }_{ x }={ upsilon }_{ 0x }+{ a }_{ x }cdot t$ находим время:

$t=frac { { upsilon }_{ x }-{ upsilon }_{ 0x } }{ { a }_{ x } } =frac { upsilon -{ upsilon }_{ 0 } }{ -a } ,quad t=50c.$

Перемещение находим из уравнения ${ s }_{ x }={ upsilon }_{ 0x }cdot t+frac { { a }_{ x }cdot { t }^{ 2 } }{ 2 }$ :

$s={ upsilon }_{ 0 }cdot t-frac { acdot { t }^{ 2 } }{ 2 }$ , s = 500 м.

2 Способ. Используются υ0, υ, a и s (надо найти).

Так как отсутствующая величина t, то применяем формулу № 4:

Задача 2. Самолет при взлете за 20 с пробегает по дорожке взлетной полосы 700 м. Какую скорость самолет имеет в конце дорожки взлетной полосы? Движение самолета считайте равноускоренным.

Решение. Скорость самолета увеличивается, поэтому ускорение направлено в сторону движения. Фраза из условия «при взлете» позволяет сделать вывод, что υ0 = 0. Ось 0Х направим по направлению начальной скорости (рис. 2), поэтому

${ s }_{ x }=s,quad { upsilon }_{ x }=upsilon ,quad { upsilon }_{ 0x }=0,quad { a }_{ x }=a$

1 способ. Из уравнения ${ s }_{ x }={ upsilon }_{ 0x }cdot t+frac { { a }_{ x }cdot { t }^{ 2 } }{ 2 }$ находим ускорение:

Конечную скорость находим из уравнения ${ upsilon }_{ x }={ upsilon }_{ 0x }+{ a }_{ x }cdot t$ :

м/с.

2 способ. Используются ${ upsilon }_{ 0 }$ , upsilon (надо найти), t и s.

Так как отсутствующая величина a, то применяем формулу № 5:

Тогда

Задача 3. Шарик в начале наклонного желоба толкнули вниз со скоростью 2 м/с. Определите скорость шарика в конце желоба, если шарик двигался с ускорением 1,25 м/с2, а длина желоба – 2 м.

Решение. Скорость шарика увеличивается, поэтому ускорение направлено в сторону движения. По условию длина желоба – это расстояние, которое пройдет шарик, и при прямолинейном движении s = l. Ось 0Х направим по направлению начальной скорости (рис. 3), поэтому

${ s }_{ x }=l,quad { upsilon }_{ x }=upsilon ,quad { upsilon }_{ 0x }={ upsilon }_{ 0 },quad { a }_{ x }=a.$

1 способ. Из уравнения ${ s }_{ x }={ upsilon }_{ 0x }cdot t+frac { { a }_{ x }cdot { t }^{ 2 } }{ 2 }$ находим время:

Получили квадратное уравнение относительно t. Корни этого уравнения:

находим конечную скорость из уравнения ${ upsilon }_{ x }={ upsilon }_{ 0x }+{ a }_{ x }cdot t$ :

$upsilon ={ upsilon }_{ 0 }+acdot t,quad upsilon =3$ м/с.

2 способ. Используются ${ upsilon }_{ 0 }$ , upsilon (надо найти), a и s.

Так как отсутствующая величина t, то применяем формулу № 4:

Тогда

Задача 4. Хоккейная шайба проскользила по льду 50 м за 2,5 с и остановилась. С каким ускорением двигалась шайба?

Решение. По условию длина поля – это расстояние, которое пройдет шайба, и при прямолинейном движении s = l. «Шайба … остановилась» следовательно, . Скорость шайбы уменьшается, поэтому ускорение направлено против движения. Ось 0Х направим по направлению начальной скорости (рис. 4), поэтому

${ s }_{ x }=l,quad { upsilon }_{ x }=0,quad { upsilon }_{ 0x }={ upsilon }_{ 0 },quad { a }_{ x }=-a$

1 способ. Данную задачу по действиям решить нельзя, т.к. в каждом уравнение неизвестны две величины (ускорение и начальная скорость). Необходимо решать систему уравнений:

или

В итоге получаем:

2 способ. Используются upsilon , a (надо найти), t и s.

Так как отсутствующая величина ${ upsilon }_{ 0 }$ , то применяем формулу № 3:

Тогда

Вывод.

1) Преимущество первого способа только в том, что нужно запомнить две формулы. При применении второго способа надо запомнить пять формул.

2) При применении первого способа вы можете решать, как линейное уравнение с одним неизвестным, так и квадратные уравнения или систему двух уравнений в общем виде. При применении второго способа вы решаете одно уравнение с одним неизвестным.

Сакович А.Л., 2020

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Задачи на равноускоренное движение» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
07.05.2023

Источник

ЗАДАЧИ на Прямолинейное равноускоренное движение с решениями

Название величины

Обозначение

Единица измерения

Формула

t

v0x

vx

ax

Sx

x

ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ

Краткое пояснение для решения ЗАДАЧИ на Прямолинейное равноускоренное движение.

Равноускоренное движение: определение и примеры

Вопросы с ответами на равноускоренное движение

Задачи на равноускоренное движение

Задача №1. Равноускоренное движение

Задача №2. Равноускоренное движение

Задача №3. Нахождение ускорения

Задача №4. Нахождение ускорения при равноускоренном движении

Задача №5. Нахождение ускорения и скорости при равноускоренном движении

Уровень А

Уровень B

Теория

Задачи

Вам также может понравиться

Как найти файл баннера

Как найти массу груза в воздухе

Как найти уникальные значения в таблице

Добавить комментарий Отменить ответ

ЗАДАЧИ на Прямолинейное равноускоренное
движение с решениями

v_0x

v_x

a_x

S_x

Краткое пояснение для решения
ЗАДАЧИ на Прямолинейное равноускоренное движение.