Задачи по физики как найти скорость

Давно планировал начать рубрику для школьников и студентов (а может и не только для них), в которой будет рассказываться о методах решения конкретных задачи и подготовке к экзаменам по физике. Само собой, в этой же рубрике мы поговорим и про егэ по физике, которое пугает ребят больше всего. Пусть рубрика на канале называется #инженер репетитор

Ну а начнем с самого простого – научимся решать задачи на скорость. Эти задачки являются базой для дальнейшего понимания кинематики и динамики, и будут вылезать на протяжении всей механики.

Давайте сначала кратенько вспомним, а что такое скорость?

Кратко про скорость в физике

Скорость в физике – это то насколько быстро изменяется некоторая физическая величина с течением времени. Векторная величина, которая имеет размер и направление.

Например, мы нагреваем комнату. Каждый час система отопления прибавляет в комнате один градус. Значит, скорость прогрева комнаты составляет один градус в час. Или едем мы на велосипеде и за один час проезжаем 20 км. Значит, мы едем со скоростью 20 километров в час.

Вот собственно и всё, что нужно помнить из теории по этому вопросу.

Задачки на скорость обычно сконцентрированы в разделе механики, но вылезают и в других более серьезных разделах физики – скорость света, время течения какой-то реакции, скорость изменения чего-то.

Однако, разобравшись как решать подобные задачи для движения чего-то материального, разобраться и в других разделах проблем не составит. Так или иначе, когда говорят про задачи на скорость, обычно подразумевают именно кинематику и динамику.

Итак, а какие собственно задачи в этой теме бывают и как их решать :)?

Задачи по скорости и их типы

Все задачи из этой темы обычно сводятся к тому, что нужно вытащить скорость из некоторой закономерности. Для этого нужно понимать и примерно помнить формулировки, связанные со скоростью. Их не так много. Не забываем и классические косяки – например привести всё к единой системе СИ.

Самые простые задачки на скорость

Самый простой случай, когда нам известно пройденное расстояние и время, а нужно найти скорость:

S = v * t, значит V = S / t

Находим скорость в м/с или км/ч.

Задачки на “встречу”

Задачки на “встречу”. Кто-то едет навстречу кому-то или кто-то кого-то встретил. Обычно такие задачки, с помощью витиеватого условия, пытаются заморочить читателю голову, но суть-то от этого не меняется.

Нам, например, задают граничные условия и указывают, что два мотоциклиста едут по одной дороге в одну сторону и выехали одновременно. Дальше они встретились. Ну и один другого подождал на точке встречи. Один едет 20 минут, а другой едет со скоростью 50 км/ч 60 минут. Найдите скорость первого мотоциклиста. Проблем быть не должно 🙂

Считаем по приведенной выше формуле сколько проехал второй мотоциклист до времени встречи. Из этого расстояния выражаем скорость первого мотоциклиста. Ведь в точке встречи расстояние, которое они проехали было одинаковым. Вот вам и решение.

Вообще, относительно, всей этой тематики, очень полезно освоить процесс рисования чертежей и схем. Нужно сделать доходчивую и понятную схему, которая будет в нужном масштабе отражать все перемещения и их особенность. Это будет залогом практически 100% успеха. Плюс внимательность!

Задачи на скорость в присутствии ускорения

Задачки на равноускоренное движение. Этот тип задач чуть сложнее. В дело вступает ускорение. Что такое ускорение? Это уже, в свою очередь, быстрота изменения скорости. Обозначается буквой а.

Обычно большая часть величин для решения такой задачи дана или выводится из нехитрой формулы:

V = Vo + аt, где V – скорость, а – ускорение, t – время движения.

В отличие от равномерного движения тело тут перемещается равноускоренно. Т.е. за каждый интервал времени скорость изменяется на одинаковую величину. Это применимо, например, к свободному падению с высоту. Пусть всё тот же мотоциклист едет первый час со скоростью 40 км/ч, а потом разгоняется до 60 км/ч и дальше ускоряется на 20 км/ч каждый час.

Опять-таки, все задачи тут завязаны на “кручу верчу обмануть хочу”. И да, на всякий случай отмечу, что все наши рассуждения из пунктов 1 и 2 тут тоже применимы, а ещё ускорение может получиться отрицательным и это не должно вас пугать.

Для решения задач из данной категории вам потребуется внимательно читать условие задачи и включить логику.

Задачки на среднюю скорость

Задачки на среднюю скорость. Тоже очень просто решаются. Что такое средняя скорость – это скорость, полученная как среднее арифметическое от скоростей на каждом из участков.

V средняя = Весь путь (S1+S2+S3+…) / всё время (t1+t2+t3+…)

Ну а дальше опять комбинаторика :). Подставь-посчитай-вырази. Ловкость рук и внимательность.

Сразу отмечу, что когда мы обсуждаем скорость или ускорение в том разрезе, как мы его видели до сих пор, мы всегда подразумевали именно среднее значение величин. Или не совсем-таки среднее, но условно разбитое на удобное для вычисления количество участков. Усредненное если желаете. В жизни же всё немного иначе.

Речь идёт о том, что если вы представите реальное движение того же несчастного мотоциклиста (или любого другого тела), о котором мы уже много раз вспомнили, он не будет ехать равномерно. Он поедет с рваным ритмом. Там на светофоре постоял. Там перед ямой затормозил. Дальше мотобат его хлопнул, документы проверяет…Бед будет много! И всё это отражается на скорости и как следствие – на ускорении. Это значит, что он действительно может проехать за час свои 50 км, но при этом за полчаса он проедет не 25 км, как мы ожидаем, а всего лишь 10 км, а дальше нагонит разницу.

Если мы высчитываем интегральный или усредненный показатель, нам в принципе-то, фиолетово. Главное, чтобы цифры сошлись. Но если нам нужно определить значение в конкретный момент, то расчёты уже будут неточные. И тут…

задачки, где есть мгновенная скорость

Что такое мгновенная скорость?

Это скорость в конкретный момент времени. Берем мотоциклиста, смотрим на его траекторию. Тыкаем пальцем в любую точку и узнаем, что там скорость пусть 10 км/ч. А через 5 минут уже 70 км/ч. А ещё через 10 минут – опять 10 км/ч. И вовсе не 50 км/ч на всём участке. Или ещё лучше – рисуем график изменения его расстояния в зависимости от времени. По такому графику всегда можно найти мгновенную скорость.

Как подступиться к подобным задачкам?

Для начала мы вспомним, что скорость это – первая производная от функции изменения расстояния по времени. Ведь производная – это и есть скорость изменения величины.

Дальше нам нужна функция, по которой изменялось расстояние. Без неё ничего решить не выйдет. Ведь данных попросту нет.

Исходя из формы кривой у нас будет её уравнение. Дальше нужно его дифференцировать.

Также в этом разделе часто вылезает некоторое дельта R. Что это такое и почему оно в формуле? Это всего лишь то самое значение расстояния (ничтожно малое), пройденного телом, за время стремящееся к нулю.

Ну и да…Для решения задач теперь нужно учитывать, что скорость мгновенная. Больше ничего не меняется.

Задачки на скорость при движении по кривой или окружности

Ещё мы можем столкнуться с понятием угловой скорости.

Начнем с того, что определим, чем вообще ситуация при движении по окружности отличается от ситуации с движением по обычной траектории? По сути дела ничем, кроме того, что путь будет высчитываться относительно окружности – будем считать длину окружности или дуги по известным всем формулам и использовать приведенные ранее зависимости для нахождения скорости.

Это тот самый случай, про который я говорю что учить без понимания бессмысленно. Ведь по сути нам сейчас нужно запомнить только формулы, приведенные раннее, а для криволинейного движения всё высчитаем, опираясь на них и понимая суть вопроса.

Но ко всему этому добавится угловая скорость. Что это? При движении материальной точки по окружности у неё есть линейная скорость, а есть угловая. Смотрим картинку.

Линейная скорость обозначена V, а угловая W (омега). Линейная скорость – это та же скорость, что мы разобрали выше. Она же мгновенная в данном случае. Скорость материальной точки, направленна по касательной к траектории.

Угловая скорость – это то, насколько быстро вращается наш радиус R. Представьте себе часы со стрелками. Стрелка вращается с некоторой скоростью, или – изменяет угол с некоторой скоростью. Вот вам и угловая скорость 🙂 И всё! Считается вот так:

Видите, логика совершенно такая же, как мы рассматривали выше.

Соответственно, в задачках на угловую скорость нужно мыслить аналогично самому первому пункту в нашем гиде. Это просто обычная материальная точка (тело) которая перемещается по окружности. Отличается только траектория ,а в отдельную тему это выделяют попросту для удобства восприятия.

Также, если есть задачка на криволинейное движение, то нужно иметь представление о виде траектории движения тела. Если траектория сложная, то её разбивают на простые геометрические формы и суммируют результаты.

Если нужно сложить скорости

Ещё бывают случаи, когда нужно выполнять сложение скоростей. Например, сложить две скорости разных тел и найти результирующую. Или сложить скорости одного тела.

Опять-таки, бояться таких задачек не нужно!

Вся логика строится из навыка оперировать с векторами.

Скорость – это величина векторная. Значит и зарисовать её можно с помощью вектора определенной длины. Вектора скорости могут быть расположены в одной плоскости или в объеме.

Советую посмотреть вот этот ролик на моем канале

Если вектора скорости находятся в одной плоскости то всё совсем просто. Чаще всего решение сводится к операциям над прямоугольными треугольниками. Бывают и очень простые случаи – векторы скорости вообще направлены вдоль одной прямой. Уже неважно разно направлены они или сонаправлены.

Чуть сложнее ситуация, если векторы скорости расположены в объеме. Там мы приходим к единичным векторам. Ситуация более геморройная, но от того не более сложная.

———————-

Итак, друзья!

Я постарался изложить все основы, которые могут помочь вам разобраться с решением задач на скорость. Очень надеюсь, что материал вам поможет.

Писать и разбирать каждую задачку – это довольно объемная штука. Такое нужно рассматривать уже в формате индивидуальных занятий.

Если я забыл осветить что-то в статье или не полностью/непонятно раскрыл теорию вопроса – пожалуйста пишите об этом в комментариях и я дополню статью и отвечу на ваш вопрос :)…Давайте вместе сделаем полезный и полный мануал. Ещё можно спросить меня в социальных сетях прямо на страничке https://vk.com/inznan или на лицекниге https://web.facebook.com/inznan

Ну и ответьте пожалуйста на вопрос, нужны ли такие материалы на моем проекте:

Средняя скорость. Решение задач по физике

Подробности

Обновлено 02.09.2018 15:56

Просмотров: 2376

Задачи по физике – это просто!

где

Sобщ – общий путь, т.е. сумма всех отрезков пути

t общ – общее время, т.е. время, за которое был пройден весь путь

При решении задач очень помогает простенький чертеж, на котором надо показать все отрезки пути.
Около каждого отрезка для наглядности укажите буквенные обозначения скорости, времени, пути (с нужным индексом) и формулы для их расчета (если это необходимо).

Задача 2

Автомобиль ехал 2 минуты со скоростью 10 м/с, а затем проехал еще 500 метров за 30 секунд.
Определить среднюю скорость движения.

Задача 4

Автомобиль проехал первую половину пути со скоростью 10 м/с, а вторую половину пути со скоростью 20 м/с. Определить среднюю скорость автомобиля на всем пути.

Пусть S – общий пройденный путь.

Задача 5

Автомобиль одну треть времени движения ехал со скоростью 10 м/с, а остальное время со скоростью 20 м/с. Определить среднюю скорость за все время движения.

Пусть t – общее время движения.

Инфоурок

›

Физика

›Другие методич. материалы›Решение задач по физике . Тема “Скорость”.

Решение задач по физике . Тема “Скорость”.

Задачи на движение с решениями

Используемые формулы в 7 классе по теме «Задачи на движение (прямолинейное равномерное)»

Название величины	Обозначение	Единицы измерения	Формула
Путь	s	м, км	s = v * t
Время	t	с, ч	t = s / v
Скорость	v	м/с, км/ч	v = s / t

1 мин = 60 с;   1 ч = 3600 с;   1 км = 1000 м;   1 м/с = 3,6 км/ч.

---

---

---

ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ

Задача № 1.
Ласточка летит со скоростью 36 км/ч. Какой путь она преодолеет за 0,5 ч?

---

Задача № 1.
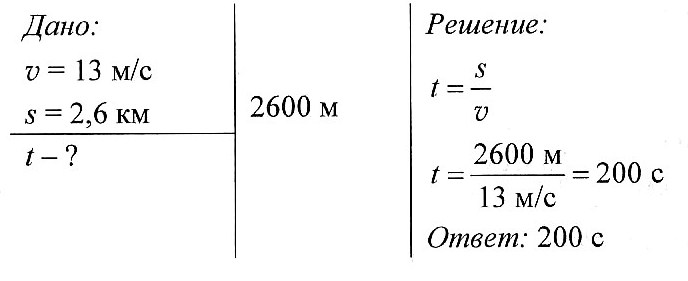
Конькобежец может развивать скорость до 13 м/с. За какое время он пробежит дистанцию длиной 2,6 км?

---

Задача № 3.
Автомобиль «Чайка» развивает скорость до 160 км/ч, а почтовый голубь — до 16 м/с. Сможет ли голубь обогнать автомобиль?

Решение. Чтобы сравнить скорости движения тел, надо перевести их в одинаковые единицы измерения. Перевод скорости из одних единиц в другие выполняют следующим образом. 160 км = 160000 м, 1 ч = 3600 с. Следовательно, за 1 с автомобиль пройдет путь 160000 : 3600 = 44 (м), значит:

Ответ: Голубь не обгонит автомобиль, так как 16 м/с < 44 м/с.

---

Задача № 4.
Вдоль дороги навстречу друг другу летят скворец и комнатная муха. На рисунке представлены графики движения скворца (I) и мухи (II). Пользуясь графиком, определите:

1) Каковы скорости движения скворца и мухи?
2) Через сколько секунд после начала движения они встретятся?
3) Какое расстояние они пролетят до места встречи?

Решение. 
1. Скорость движения скворца определим по формуле v=S/t. Выберем на графике произвольное время и определим, какое расстояние за это время пролетел скворец. Видно, что за 5 с скворец пролетел 100 м. Тогда

Аналогично найдем скорость движения мухи:

2. Точка А (точка пересечения графиков движения) соответствует моменту встречи. Скворец и муха встретятся через 4 секунды.

3. Скворец до места встречи пролетит расстояние S_I = 80 м. Муха пролетит расстояние S_II = 100 м — 80 м = 20 м.

Ответ: 1) скворец 20 м/с,  муха 5 м/с,   2) через 4 с,   3) скворец 80 м, муха 20 м

---

Задача № 5.
 Определите среднюю скорость движения плота, если за 20 минут он переместился на 900 м. Скорость выразить в км/ч.

Ответ: Средняя скорость плота 2,7 км/ч.

---

Задача № 6.
 Стоящий на эскалаторе человек поднимается за 2 мин, а бегущий по эскалатору — за 40 с. За какое время этот человек поднимется по неподвижному эскалатору?

ОТВЕТ: 1 мин.

---

Задача № 7.
 Моторная лодка за 3 ч проходит расстояние от города до поселка, расположенного ниже по течению реки. Сколько времени займет обратный путь, если скорость движения лодки относительно воды в 4 раза больше скорости течения?

ОТВЕТ: 5 ч.

---

Задача № 8 (повышенной сложности).
  Рыбак плыл по реке на лодке, зацепил шляпой за мост, и она свалилась в воду. Через час рыбак спохватился, повернул обратно и подобрал шляпу на 4 км ниже моста. Какова скорость течения? Скорость лодки относительно воды оставалась неизменной по модулю.

ОТВЕТ: 2 км/ч.

---

Задача № 9 (олимпиадного уровня).
  Из городов А и Б навстречу друг другу по прямому шоссе одновременно выехали два велосипедиста. Скорость первого 10 км/ч, скорость второго 15 км/ч. Одновременно с велосипедистами из города А вылетела ласточка. Она долетает до второго велосипедиста, разворачивается, Долетает до первого велосипедиста и летает так между ними до тех пор, пока велосипедисты не встретятся. Какой путь пролетела ласточка, если скорость ее движения 50 км/ч, а расстояние между городами 100 км? Временем разворота ласточки можно пренебречь.

ОТВЕТ: 200 км.

---

Алгоритм решения задач на движение

При решении других задач прямолинейного равномерного движения в общем виде нужно придерживаться следующего алгоритма: 1) выбрать систему отсчёта; 2-3) определить начальные координаты и значения скоростей движения тел в этой системе отсчёта; 4) записать зависимости координат тел от времени; 5) записать в виде уравнения условие задачи; 6) объединить уравнения; 7) решить эти уравнения; 8) провести анализ полученного результата (после чего выяснить, имеет ли полученный результат физический смысл); 9) если в условии задачи даны числовые значения, необходимо подставить их в полученное выражение и получить числовой ответ.

Анализ полученного результата заключается в исследовании зависимости искомой величины от входящих в ответ величин.

Не стоит забывать и про направление движения в зависимости от типа задачи (встреча, погоня, обгон, отставание)

---

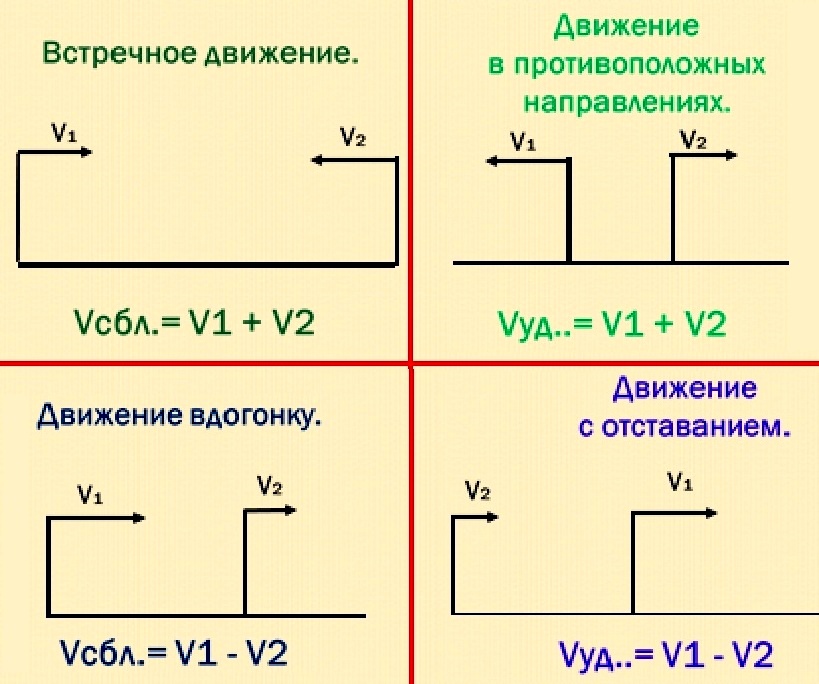
Конспект урока «Задачи на движение с решением».

Следующая тема: «Задачи на плотность, массу и объем«.

1. Задача №1

Ав­то­мо­биль дви­жет­ся с се­ве­ра на юг со ско­ро­стью 90 км/ч. Необ­хо­ди­мо вы­ра­зить эту ско­рость в мет­рах в се­кун­ду и изоб­ра­зить гра­фи­че­ски.

Рис. 1. К усло­вию за­да­чи № 1

Усло­вие и ре­ше­ние дан­ной за­да­чи не тре­бу­ют спе­ци­аль­но­го оформ­ле­ния. Вна­ча­ле нужно пе­ре­ве­сти ско­рость 90 км/ч в метры в се­кун­ду, в си­сте­му СИ. 90 км/ч можно за­пи­сать как 90 000 мет­ров, де­лен­ные на 3600 се­кунд. Если про­ве­сти ма­те­ма­ти­че­ский рас­чет, то мы по­лу­чим, что 90 км/ч со­от­вет­ству­ет 25 м/с.

Затем вы­бе­рем мас­штаб изоб­ра­же­ние век­то­ра ско­ро­сти ав­то­мо­би­ля. На­при­мер, одна кле­точ­ка вашей тет­ра­ди будет со­от­вет­ство­вать 5 м/с. Тогда, чтобы изоб­ра­зить век­тор ско­ро­сти, чис­лен­но рав­ный 25 м/с, в вы­бран­ном мас­шта­бе нужно изоб­ра­зить стрел­ку, на­прав­лен­ную с се­ве­ра на юг (т.е., свер­ху вниз), дли­ной в 5 кле­то­чек. Рядом ста­вим обо­зна­че­ние: сим­вол v, обо­зна­ча­ю­щий ско­рость, с ма­лень­кой стрел­кой над ним – зна­ком век­то­ра.

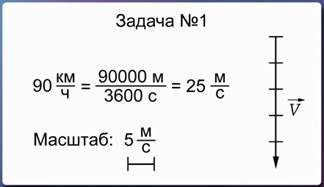
Рис. 2. К ре­ше­нию за­да­чи № 1

2. Задача №2

За 20 минут тело пе­ре­ме­сти­лось на 6000 см. Необ­хо­ди­мо опре­де­лить ско­рость дви­же­ния дан­но­го тела. 

Такие за­да­чи в фи­зи­ке на­зы­ва­ют­ся ко­ли­че­ствен­ны­ми, по­то­му что как усло­вие, так и ответ со­дер­жат чис­ло­вые дан­ные. Ре­ше­ние по­доб­ных задач тре­бу­ет спе­ци­аль­но­го оформ­ле­ния, с ко­то­рым мы сей­час по­зна­ко­мим­ся.

В левом углу тет­рад­но­го листа за­пи­сы­ва­ем слово «Дано:», ста­вим двое­то­чие и ниже в стол­бик пе­ре­чис­ля­ем за­дан­ные ве­ли­чи­ны и через знак ра­вен­ства их чис­ло­вые зна­че­ния с раз­мер­но­стью. Далее от­чер­ки­ва­ем дан­ные вер­ти­каль­ной и пер­пен­ди­ку­ляр­ной ей го­ри­зон­таль­ной чер­той, под чер­той пишем слово «Найти:», ука­зы­ва­ем, какую фи­зи­че­скую ве­ли­чи­ну нам необ­хо­ди­мо найти в этой за­да­че, ста­вим знак ра­вен­ства и знак во­про­са.

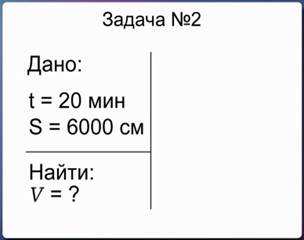
Рис.  3. Оформ­ле­ние крат­ко­го усло­вия за­да­чи

Ве­ли­чи­ны в усло­вии дан­ной за­да­чи за­да­ны во вне­си­стем­ных еди­ни­цах – сан­ти­мет­рах и ми­ну­тах. По­это­му спра­ва от вер­ти­каль­ной черты мы ста­вим обо­зна­че­ние «СИ» (ин­тер­на­ци­о­наль­ная си­сте­ма) и про­из­во­дим пе­ре­вод еди­ниц в си­сте­му СИ. 20 мин – это 1200 с, а 6000 см – это 60 м. Пра­вее ко­лон­ки чисел ста­вим еще одну вер­ти­каль­ную черту.

Рис. 4. Пе­ре­вод еди­ниц в си­сте­му СИ

На остав­шем­ся спра­ва сво­бод­ном про­стран­стве свер­ху пишем слово «Ре­ше­ние:».

В фи­зи­ке при­ня­то сна­ча­ла за­пи­сы­вать фор­му­лу, с по­мо­щью ко­то­рой будут про­из­во­дить­ся рас­че­ты. Чтобы найти ско­рость, необ­хо­ди­мо прой­ден­ный телом путь раз­де­лить на время дви­же­ния тела. Затем при­ня­то де­лать про­вер­ку раз­мер­но­сти (еди­ниц из­ме­ре­ния) по­лу­чен­но­го ре­зуль­та­та. Раз­мер­но­сти ве­ли­чин, вхо­дя­щих в фор­му­лы, за­пи­сы­ва­ют в квад­рат­ных скоб­ках. Мы по­лу­ча­ем, что ско­рость из­ме­ря­ет­ся в мет­рах в се­кун­ду.

Сле­ду­ю­щий этап – под­ста­нов­ка в фор­му­лу чис­ло­вых дан­ных. Еще раз за­пи­сы­ва­ем букву, обо­зна­ча­ю­щую ско­рость, но вме­сто букв, обо­зна­ча­ю­щих путь и время, за­пи­сы­ва­ем чис­лен­ные зна­че­ния этих ве­ли­чин и вы­пол­ня­ем вы­чис­ле­ния. Деля 60 на 1200, по­лу­ча­ем зна­че­ние 0,05 – это и есть ис­ко­мое зна­че­ние ско­ро­сти. В круг­лых скоб­ках мы за­пи­сы­ва­ем раз­мер­ность по­лу­чив­шей­ся ве­ли­чи­ны (метры в се­кун­ду).

Внизу пишем слово «Ответ», ста­вим двое­то­чие и еще раз ука­зы­ва­ем чис­ло­вое зна­че­ние ско­ро­сти с раз­мер­но­стью.

Рис 5. Пол­но­стью оформ­лен­ное ре­ше­ние за­да­чи № 2

3. Задача №3

За­да­чи, по­доб­ные этой, часто ис­поль­зу­ют­ся при вы­пол­не­нии те­сто­вых за­да­ний. В них есть усло­вие и несколь­ко ва­ри­ан­тов от­ве­тов, из ко­то­рых необ­хо­ди­мо вы­брать пра­виль­ный.

По гра­фи­ку за­ви­си­мо­сти пути, прой­ден­но­го телом, от вре­ме­ни, необ­хо­ди­мо опре­де­лить ско­рость тела, дви­жу­ще­го­ся рав­но­мер­но и пря­мо­ли­ней­но.

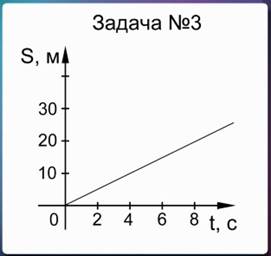
Рис. 6. К усло­вию за­да­чи № 3

Так как в усло­вии за­да­чи ука­за­но, что дви­же­ние рав­но­мер­ное, то можно взять любую точку на гра­фи­ке. Лучше всего вы­би­рать точку, ко­то­рая рас­по­ло­же­на про­тив штри­хов на осях гра­фи­ка. Про­ве­дем пунк­тир­ные линии пер­пен­ди­ку­ляр­но осям пути и вре­ме­ни, чтобы найти, какой путь про­шло тело за опре­де­лен­ный про­ме­жу­ток вре­ме­ни. В нашем слу­чае, на­при­мер, за 4 се­кун­ды тело про­шло путь 10 мет­ров. Затем по фор­му­ле рас­счи­та­ем зна­че­ние ско­ро­сти. Раз­де­лив 10 м на 4 с, по­лу­чим, что ско­рость тела равна 2,5 м/с. Сле­до­ва­тель­но, пра­виль­ным яв­ля­ет­ся ответ «В».

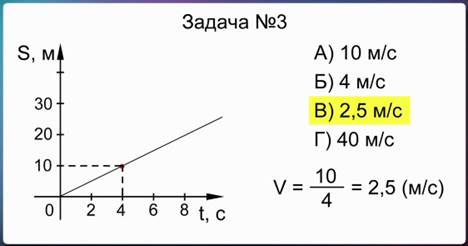
Рис. 7. Ре­ше­ние за­да­чи № 3