Задачи на Сопротивление проводников с решениями
Формулы, используемые на уроках «Задачи на сопротивление проводников»:
Название величины |
Обозначение |
Единица измерения |
Формула |
Сила тока |
I |
А |
I = U / R |
Напряжение |
U |
В |
U = IR |
Сопротивление |
R |
Ом |
R = U/I |
Длина проводника |
l |
м |
l = RS / p |
Площадь поперечного сечения проводника |
S |
мм2 |
S = pl / R |
Удельное сопротивление вещества |
p |
Ом • мм2 /м
|
p = RS / l |
Сопротивление проводника |
R |
Ом |
R = pl / S |
Площадь поперечного сечения измеряют в мм2, поэтому в справочниках значения удельного сопротивления проводника приводятся не только в единицах СИ Ом • м, но в Ом • мм2 / м.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Длина алюминиевого провода 500 м, площадь его поперечного сечения 4 мм2 , Чему равно сопротивление провода?

Задача № 2.
Медный провод с площадью поперечного сечения 0,85 мм2 обладает сопротивлением 4 Ом. Какова длина провода?

Задача № 3.
Длина серебряного провода 0,6 м, а сопротивление 0,015 Ом. Определите площадь поперечного сечения провода.

Задача № 4.
Жила алюминиевого провода, используемого для электропроводки, имеет площадь поперечного сечения 2 мм2. Какой площадью поперечного сечения должен обладать никелиновый провод, чтобы длина и сопротивление линии не изменились?

Задача № 5.
Площади поперечных сечений стальных проволок с одинаковыми длинами равны 0,05 и 1 мм2. Какая из них обладает меньшим сопротивлением; во сколько раз?

Задача № 6.
Сопротивление проволоки длиной 1 км равно 5,6 Ом. Определите напряжение на каждом участке проволоки длиной 100 м, если сила тока в ней 7 мА.

Задача № 7.
Имеются два однородных проводника, однако первый в 8 раз длиннее второго, который имеет вдвое большую площадь поперечного сечения. Какой из проводников обладает большим сопротивлением; во сколько раз?

Задача № 8.
Шнур, употребляемый для подводки тока к телефону, для гибкости делают из многих тонких медных проволок. Рассчитайте сопротивление такого провода длиной 3 м, состоящего из 20 проволок площадью поперечного сечения 0,05 мм2 каждая.

Задача № 9.
Определите силу тока, проходящего через реостат, изготовленный из никелиновой проволоки длиной 50 м и площадью поперечного сечения 1 мм2, если напряжение на зажимах реостата равно 45 В.

Задача № 10.
Сопротивление проволоки, у которой площадь поперечного сечения 0,1 мм2, равно 180 Ом. Какой площади поперечного сечения надо взять проволоку той же длины и из того же материала, чтобы получить сопротивление 36 Ом?

Краткая теория для решения
Задачи на Сопротивление проводников.

Таблица удельного электрического сопротивления
некоторых веществ при 20 °С.

Это конспект по теме «ЗАДАЧИ на Сопротивление проводников». Выберите дальнейшие действия:
- Перейти к теме: ЗАДАЧИ на Последовательное соединение проводников
- Посмотреть конспект по теме Электрическое сопротивление
- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.
Сила тока в цепи определяется электрическим зарядом, проходящим через поперечное сечение проводника за единицу времени: $I = frac{q}{t}$.
Электрическое напряжение — это еще одна физическая величина, характеризующая электрическое поле. Она равна отношению работы тока на данном участке к электрическому заряду, прошедшему по этому участку: $U = frac{A}{q}$.
Электрическое сопротивление — величина, зависящая от свойств проводника. На значение сопротивления не влияет ни значение силы тока в проводнике, ни значение напряжения на его концах. Его можно рассчитать по формуле $R = frac{rho l}{S}$, где $rho$ — удельное сопротивление проводника, $l$ — длина проводника, $S$ — площадь его поперечного сечения. Значение удельного сопротивления для определенного вещества можно посмотреть в таблице 1 в уроке «Расчет сопротивления проводника. Удельное сопротивление».
Эти три физические величины (силу тока, напряжение и сопротивление) связывает между собой закон Ома для участка цепи: $I = frac{U}{R}$. Сила тока в проводнике прямо пропорциональна напряжению на его концах и обратно пропорциональна его сопротивлению.
В данном уроке вы научитесь использовать эти знания для решения задач. Мы рассмотрим несколько примеров, а затем перейдем к упражнениям и их подробным решениям.
Пример задачи №1
Длина медного провода, использованного в осветительной сети, $100 space м$, площадь поперечного сечения его $2 space мм^2$. Чему равно сопротивление такого провода?
Для того, чтобы рассчитать сопротивление такого проводника, нам понадобится значение его удельного сопротивления. Удельное сопротивление меди равно $0.017 frac{Ом cdot мм^2}{м}$. Так как эта величина нам дана именно в этих единицах измерения, мы не будем переводить в СИ значение площади поперечного сечения, выраженное в $мм^2$.
Теперь мы можем записать условие задачи и решить ее.
Дано:
$l = 100 space м$
$S = 2 space мм^2$
$rho = 0.017 frac{Ом cdot мм^2}{м}$
$R — ?$
Решение:
Формула для расчета сопротивления проводника:
$R = frac{rho l}{S}$.
Рассчитаем его:
$R = frac{0.017 frac{Ом cdot мм^2}{м} cdot 100 space м}{2 space мм^2} = frac{1.7 space Ом}{2} = 0.85 space Ом$.
Ответ: $R = 0.85 space Ом$.
Пример задачи №2
Никелиновая проволока длиной $120 space м$ и площадью поперечного сечения $0.5 space мм^2$ включена в цепь с напряжением $127 space В$. Определить силу тока в проволоке.
Табличное значение удельного сопротивления никелина равно $0.4 frac{Ом cdot мм^2}{м}$.
Перейдем к записи условия задачи и ее решению.
Дано:
$l = 120 space м$
$S = 0.5 space мм^2$
$U = 127 space В$
$rho = 0.4 frac{Ом cdot мм^2}{м}$
$I — ?$
Решение:
Силу тока мы можем рассчитать, используя формулу закона Ома для участка цепи:
$I = frac{U}{R}$.
Но мы не знаем значения сопротивления проводника. Его мы тоже можем вычислить:
$R = frac{rho cdot l}{S}$,
$R = frac{0.4 frac{Ом cdot мм^2}{м} cdot 120 space м}{0.5 space мм^2} = frac{48 space Ом}{0.5} = 96 space Ом$.
Теперь мы можем рассчитать силу тока:
$I = frac{127 space В}{96 space Ом} approx 1.3 space А$.
Ответ: $I approx 1.3 space А$.
Пример задачи №3
Манганиновая проволока длиной $8 space м$ и площадью поперечного сечения $0.8 space мм^2$ включена в цепь аккумулятора. Сила тока в цепи $0.3 space А$. Определить напряжение на полюсах аккумулятора.
Табличное значение удельного сопротивления манганина равно $0.43 frac{Ом cdot мм^2}{м}$.
Запишем условие задачи и решим ее.
Дано:
$l = 8 space м$
$S = 0.8 space мм^2$
$I = 0.3 space А$
$rho = 0.43 frac{Ом cdot мм^2}{м}$
$U — ?$
Решение:
Если в условии задачи сказано, что проводник включен в цепь аккумулятора, это означает, что напряжение на полюсах аккумулятора будет равно напряжению на концах проволоки.
Почему? Взгляните на такую электрическую цепь (рисунок 1). Она состоит только из проводника и аккумулятора.
Если мы захотим измерить напряжение на полюсах аккумулятора c помощью вольтметра, то параллельно подключим его в эту цепь (рисунок 2). А если захотим измерить напряжение на концах проводника? Мы подключим вольтметр точно так же. Получается, что вольтметр подключен параллельно одновременно и к источнику тока, и к проводнику. Поэтому напряжение на концах проводника — это то же самое напряжение на полюсах аккумулятора.
Запишем закон Ома:
$I = frac{U}{R}$.
Выразим из него напряжение, которое нужно найти:
$U = IR$.
Сопротивление проводника рассчитаем по формуле $R = frac{rho cdot l}{S}$.
$R = frac{0.43 frac{Ом cdot мм^2}{м} cdot 8 space м}{0.8 space мм^2} = frac{3.44 space Ом}{0.8} = 4.3 space Ом$.
Теперь мы можем рассчитать напряжение:
$U = 0.3 space А cdot 4.3 space Ом = 1.29 space В approx 1.3 space В$.
Ответ: $U approx 1.3 space В$.
Упражнения
Упражнение №1
Длина одного провода $20 space см$, другого — $1.6 space м$. Площадь сечения и материал проводов одинаковы. У какого провода сопротивление больше и во сколько раз?
Обратите внимание, что если материал проводников один и тот же, то одинаковы и значения удельных сопротивлений $rho$ для этих проводников.
Дано:
$l_1 = 20 space см$
$l_2 = 1.6 space м$
$S_1 = S_2 = S$
$rho_1 = rho_2 = rho$
СИ:
$l_1 = 0.2 space м$
$frac{R_2}{R_1} — ?$
Показать решение и ответ
Скрыть
Решение:
Сопротивление проводника рассчитывается по формуле $R = frac{rho cdot l}{S}$.
Сопротивление первого провода:
$R_1 = frac{rho_1 l_1}{S_1} = frac{rho l_1}{S}$.
Сопротивление второго провода:
$R_2 = frac{rho_2 l_2}{S_2} = frac{rho l_2}{S}$.
Теперь сравним их между собой:
$frac{R_2}{R_1} = frac{frac{rho l_2}{S}}{frac{rho l_1}{S}} = frac{l_2}{l_1}$.
Подставим численные значения длины проводов:
$frac{R_2}{R_1} = frac{1.6 space м}{0.2 space м} = 8$.
Получается, что сопротивление второго провода больше сопротивления первого в 8 раз.
Это логично, ведь вы знаете, что чем больше длина проводника, тем больше его сопротивление.
Ответ: сопротивление второго провода больше сопротивления первого в 8 раз.
Упражнение №2
Рассчитайте сопротивления следующих проводников, изготовленных из:
- Алюминиевой проволоки длиной $80 space см$ и площадью поперечного сечения $0.2 space мм^2$
- Никелиновой проволоки длиной $400 space см$ и площадью поперечного сечения $0.5 space мм^2$
- Константановой проволоки длиной $50 space см$ и площадью поперечного сечения $0.005 space см^2$
Для решения этой задачи нам понадобятся табличные значения удельного сопротивления для веществ, из которых изготовлены проволоки. Удельное сопротивление алюминия — $0.028 frac{Ом cdot мм^2}{м}$, никелина — $0.4 frac{Ом cdot мм^2}{м}$, константана — $0.5 frac{Ом cdot мм^2}{м}$.
Обратите внимание на единицы измерения удельных сопротивлений, длин и площадей проводников. Для корректных расчетов длину каждой проволоки мы переведем в СИ (в $м^2$). Площади поперечных сечений должны быть выражены в $мм^2$. Для третьего задания переведем $см^2$ в $см^2$.
Дано:
$l_1 = 80 space см$
$l_2 = 400 space см$
$l_3 = 50 space см$
$S_1 = 0.2 space мм^2$
$S_2 = 0.5 space мм^2$
$S_3 = 0.005 space см^2 = 0.5 space мм^2$
$rho_1 = 0.028 frac{Ом cdot мм^2}{м}$
$rho_2 = 0.4 frac{Ом cdot мм^2}{м}$
$rho_3 = 0.5 frac{Ом cdot мм^2}{м}$
СИ:
$l_1 = 0.8 space м$
$l_2 = 4 space м$
$l_3 = 0.5 space м$
$R_1 — ?$
$R_2 — ?$
$R_3 — ?$
Показать решение и ответ
Скрыть
Решение:
Формула для расчета сопротивления проводника: $R = frac{rho l}{S}$.
Рассчитаем по ней сопротивление каждого проводника.
$R_1 = frac{rho_1 l_1}{S_1}$,
$R_1 = frac{0.028 frac{Ом cdot мм^2}{м} cdot 0.8 space м}{0.2 space мм^2} = frac{0.0224 space Ом}{0.2} = 0.112 space Ом$.
$R_2 = frac{rho_2 l_2}{S_2}$,
$R_2 = frac{0.4 frac{Ом cdot мм^2}{м} cdot 4 space м}{0.5 space мм^2} = frac{1.6 space Ом}{0.5} = 3.2 space Ом$.
$R_3 = frac{rho_3 l_3}{S_3}$,
$R_2 = frac{0.5 frac{Ом cdot мм^2}{м} cdot 0.5 space м}{0.5 space мм^2} = frac{0.25 space Ом}{0.5} = 0.5 space Ом$.
Ответ: $R_1 = 0.112 space Ом$, $R_2 = 3.2 space Ом$, $R_3 = 0.5 space Ом$.
Упражнение №3
Спираль электрической плитки изготовлена из нихромовой проволоки длиной $13.75 space м$ и площадью поперечного сечения $0.1 space мм^2$. Плитка рассчитана на напряжение $220 space В$. Определите силу тока в спирали плитки.
Удельное сопротивление нихрома равно $1.1 frac{Ом cdot мм^2}{м}$.
Дано:
$l = 13.75 space м$
$S = 0.1 space мм^2$
$U = 220 space В$
$rho = 1.1 frac{Ом cdot мм^2}{м}$
$I — ?$
Показать решение и ответ
Скрыть
Решение:
Силу тока в спирали плитки мы можем рассчитать, используя формулу закона Ома для участка цепи: $I = frac{U}{R}$.
Неизвестное сопротивление нихромовой проволоки рассчитаем по формуле $R = frac{rho l}{S}$.
$R = frac{1.1 frac{Ом cdot мм^2}{м} cdot 13.75 space м}{0.1 space мм^2} = frac{15.125 space Ом}{0.1} = 151.25 space Ом$.
Рассчитаем теперь силу тока:
$I = frac{220 space В}{151.25 space Ом} approx 1.5 space А$.
Ответ: $I approx 1.5 space А$.
Упражнение №4
Сила тока в железном проводнике длиной $150 space мм$ и площадью поперечного сечения $0.02 space мм^2$ равна $250 space мА$. Каково напряжение на концах проводника?
Для решения задачи нам понадобится значение удельного сопротивления. Для железа оно равна $0.1 frac{Ом cdot мм^2}{м}$.
Дано:
$I = 250 space мА$
$l = 150 space мм$
$S = 0.02 space мм^2$
$rho = 0.1 frac{Ом cdot мм^2}{м}$
СИ:
$I = 0.25 space А$
$l = 0.15 space м$
$U — ?$
Показать решение и ответ
Скрыть
Решение:
Закон Ома для участка цепи: $I = frac{U}{R}$.
Выразим отсюда напряжение: $U = IR$.
Рассчитаем сопротивление проводника:
$R = frac{rho l}{S}$,
$R = frac{0.1 frac{Ом cdot мм^2}{м} cdot 0.15 space м}{0.02 space мм^2} = frac{0.015 space Ом}{0.02} = 0.75 space Ом$.
Теперь мы можем рассчитать напряжение на концах проводника:
$U = 0.25 space А cdot 0.75 space Ом approx 0.2 space В$.
Ответ: $U approx 0.2 space В$.
Знание закона Ома на сегодняшний день – вопрос общей эрудиции каждого человека. В сегодняшней статье займемся решением задач по теме «закон Ома».
Подписывайтесь на наш телеграм и получайте интересные новости каждый день! А если хотите получить скидку и не упустить выгоду – загляните на наш второй канал с приятными акциями и бонусами для клиентов.
Закон Ома: задачи с решением
Для новичков, которые только начинают решать задачи по физике, мы подготовили специальную памятку и собрали вместе более 40 формул по разным темам. Берите и пользуйтесь!
Задача на закон Ома №1
Условие
Определите силу тока в медном проводнике сеченим 0,5 мм2, если длина проводника 100 м, а напряжение на его концах равно 6,8 В.
Решение
Сначала запишем закон Ома:
I=UR
В данном случае, чтобы найти силу тока I, нужно определить сопротивление R. Используем формулу с удельным сопротивлением и перепишем выражение для закона Ома:
R=ρlSI=USρl
Осталось подставить числа и рассчитать:
I=6,8·0,50,017·100=2 А
Значение удельного сопротивления «ро» для меди берется из таблиц. Для меди ρ=0,017Ом·мм2м
Ответ: 2 А.
Задача на закон Ома №2
Условие
По вольфрамовой проволоке длиной 3 м протекает электрический ток силой 0,04 А. Проволока находится под напряжением 5 В. Определите величину площади поперечного сечения проволоки.
Решение
Выразим площадь поперечного сечения проводника из формулы для сопротивления:
R=ρlSS=ρlR
Сопротивление R найдем из закона Ома:
I=URR=UI
Подставим выражение для R в формулу для S и рассчитаем:
S=ρl·IU=0,055·3·0,045=0,0013 мм2
Ответ: 0,0013 мм2
Задача на закон Ома №3
Условие
Каково напряжение на неоднородном участке цепи?
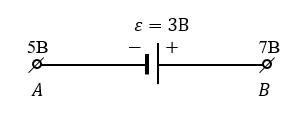
Решение
По закону Ома для неоднородного участка цепи:
U12=φ1-φ2+ε
Считая началом участка точку A, а концом – точку B, и беря поэтому ЭДС со знаком плюс (внутри источника направление тока от отрицательного полюса к положительному), получаем:
UAB=φA-φB+ε=5-7+3=1 В
Ответ: 1В.
Нужно больше примеров решений задач? Вы найдете их в нашем блоге!
Задача на закон Ома №4
Условие
Какова сила тока в резисторе, если его сопротивление 12 Ом, а напряжение на нем 120 В?
Решение
Это простейшая задача на закон Ома для участка цепи, которая решается в одно действие. Просто записываем закон Ома и производим расчет:
I=UR=12012=10 А
Ответ: 10 А.
Задача на закон Ома №5
Условие
Источник постоянного тока с ЭДС E = 12 В и внутренним сопротивлением г = 1 Ом замкнут на внешнее сопротивление R = 9 Ом. Определить силу тока в цепи I, падение напряжения UR на внешнем участке и падение напряжения Ur на внутреннем участке цепи.
Решение
Это задача на закон Ома для полной цепи. По закону Ома для замкнутой цепи:
I=εR+r=129+1=1,2 А
Падение напряжения на внешнем участке цепи:
UR=I·R=εRR+r=12·99+1=10,8 В
Падение напряжение на внутреннем участке цепи:
Ur=ε-UR=12-10,8=1,2 В
Ответ: 1,2 А; 10,8 В; 1,2 В.
Школьный учитель Георг Симон Ом открыл свой закон в 1826 году. Подробнее об истории открытия и самом законе Ома читайте в нашем блоге.
Вопросы на закон Ома
Вопрос 1. Сформулируйте закон Ома для однородного участка цепи.
Ответ. Закон Ома для однородного участка цепи нласит:
Ток прямо пропорционален напряжению и обратно пропорционален сопротивлению.
Вопрос 2. Сформулируйте закон Ома для замкнутой цепи.
Ответ. Закон Ома для замкнутой цепи гласит:
Величина тока в замкнутой цепи, состоящей из источника тока, обладающего внутренним и внешним нагрузочным сопротивлениями, равна отношению электродвижущей силы источника к сумме внутреннего и внешнего сопротивлений.
Вопрос 3. От чего зависит сопротивление цепи?
Ответ. Сопротивление вещества обусловлено колебанием атомов кристаллической решетки.
Сопротивление зависит от:
- температуры;
- материала;
- поперечного сечения проводника.
Вопрос 4. Зависит ли сопротивление от напряжения и силы тока?
Ответ. Нет. Сопротивление не зависит от напряжения и силы тока в проводнике.
Вопрос 5. Всегда ли соблюдается закон Ома?
Ответ. Нет, не всегда. Например, закон Ома не действует при низких температурах для веществ, обладающих сверхпроводимостью.
Проблемы с учебой? Обращайтесь в профессиональный сервис для студентов за квалифицированной помощью.
Задачи на Сопротивление проводников с решениями
Формулы, используемые на уроках «Задачи на сопротивление проводников».
|
Название величины |
Обозначение |
Единица измерения |
Формула |
|
Сила тока |
I |
А |
I = U / R |
|
Напряжение |
U |
В |
U = IR |
|
Сопротивление |
R |
Ом |
R = U/I |
|
Длина проводника |
l |
м |
l = RS / p |
|
Площадь поперечного сечения проводника |
S |
мм2 |
S = pl / R |
|
Удельное сопротивление вещества |
p |
Ом • мм2 /м |
p = RS / l |
|
Сопротивление проводника |
R |
Ом |
R = pl / S |
Краткая теория для решения Задачи на Сопротивление проводников.
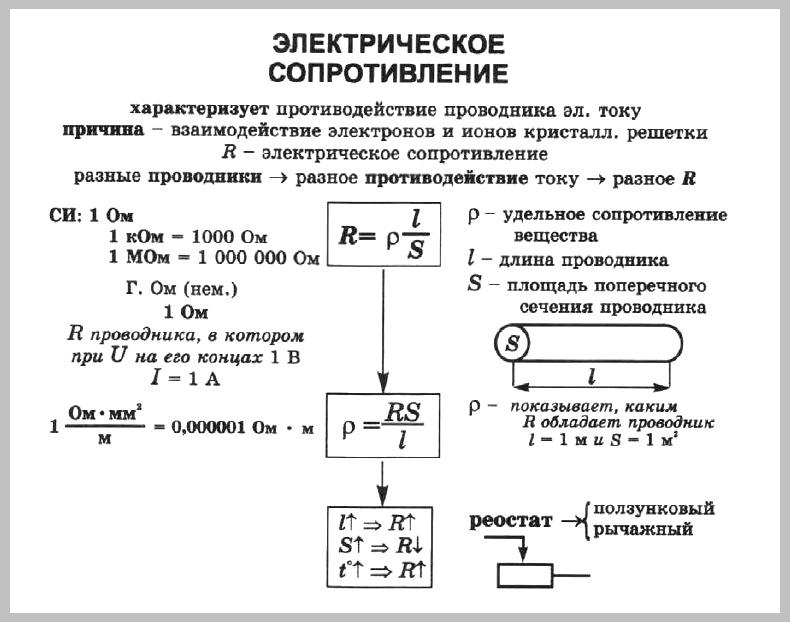
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1. Длина алюминиевого провода 500 м, площадь его поперечного сечения 4 мм2 , Чему равно сопротивление провода?

Задача № 2. Медный провод с площадью поперечного сечения 0,85 мм2 обладает сопротивлением 4 Ом. Какова длина провода?

Задача № 3. Длина серебряного провода 0,6 м, а сопротивление 0,015 Ом. Определите площадь поперечного сечения провода.
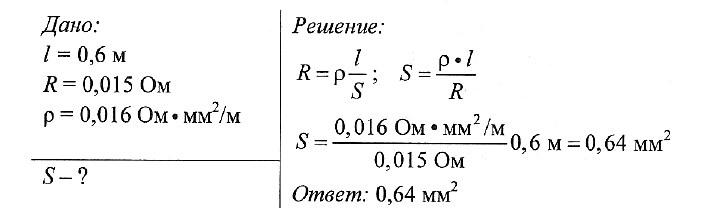
Задача № 4. Жила алюминиевого провода, используемого для электропроводки, имеет площадь поперечного сечения 2 мм2. Какой площадью поперечного сечения должен обладать никелиновый провод, чтобы длина и сопротивление линии не изменились?

Задача № 5. Площади поперечных сечений стальных проволок с одинаковыми длинами равны 0,05 и 1 мм2. Какая из них обладает меньшим сопротивлением; во сколько раз?

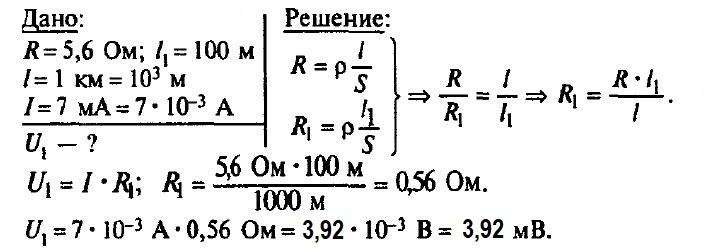
Задача № 6. Сопротивление проволоки длиной 1 км равно 5,6 Ом. Определите напряжение на каждом участке проволоки длиной 100 м, если сила тока в ней 7 мА.
Задача № 7. Имеются два однородных проводника, однако первый в 8 раз длиннее второго, который имеет вдвое большую площадь поперечного сечения. Какой из проводников обладает большим сопротивлением; во сколько раз?
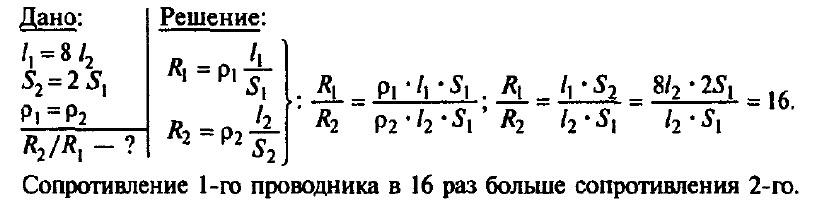
Задача № 8. Шнур, употребляемый для подводки тока к телефону, для гибкости делают из многих тонких медных проволок. Рассчитайте сопротивление такого провода длиной 3 м, состоящего из 20 проволок площадью поперечного сечения 0,05 мм2 каждая.
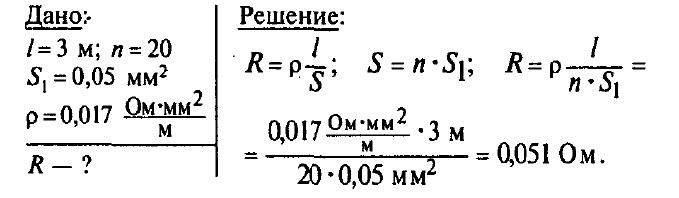
Задача № 9. Определите силу тока, проходящего через реостат, изготовленный из никелиновой проволоки длиной 50 м и площадью поперечного сечения 1 мм2, если напряжение на зажимах реостата равно 45 В.
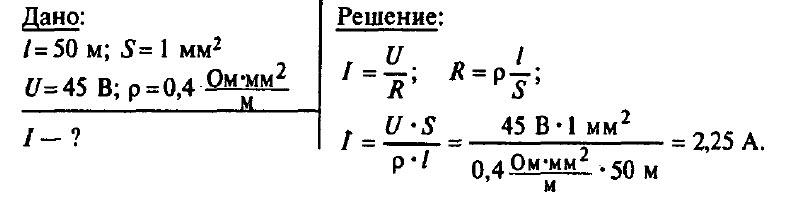
Задача № 10. Сопротивление проволоки, у которой площадь поперечного сечения 0,1 мм2, равно 180 Ом. Какой площади поперечного сечения надо взять проволоку той же длины и из того же материала, чтобы получить сопротивление 36 Ом?
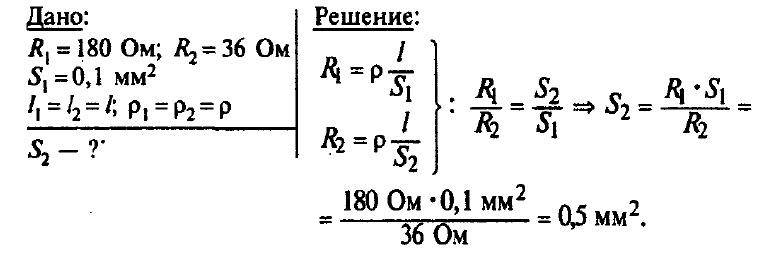
Задача № 1. Длина алюминиевого провода 500 м, площадь его поперечного сечения 4 мм2 , Чему равно сопротивление провода?
Задача № 2. Медный провод с площадью поперечного сечения 0,85 мм2 обладает сопротивлением 4 Ом. Какова длина провода?
Задача № 3. Длина серебряного провода 0,6 м, а сопротивление 0,015 Ом. Определите площадь поперечного сечения провода.
Задача № 4. Жила алюминиевого провода, используемого для электропроводки, имеет площадь поперечного сечения 2 мм2. Какой площадью поперечного сечения должен обладать никелиновый провод, чтобы длина и сопротивление линии не изменились?
Задача № 5. Площади поперечных сечений стальных проволок с одинаковыми длинами равны 0,05 и 1 мм2. Какая из них обладает меньшим сопротивлением; во сколько раз?
Задача № 6. Сопротивление проволоки длиной 1 км равно 5,6 Ом. Определите напряжение на каждом участке проволоки длиной 100 м, если сила тока в ней 7 мА.
Задача № 7. Имеются два однородных проводника, однако первый в 8 раз длиннее второго, который имеет вдвое большую площадь поперечного сечения. Какой из проводников обладает большим сопротивлением; во сколько раз?
Задача № 8. Шнур, употребляемый для подводки тока к телефону, для гибкости делают из многих тонких медных проволок. Рассчитайте сопротивление такого провода длиной 3 м, состоящего из 20 проволок площадью поперечного сечения 0,05 мм2 каждая.
Задача № 9. Определите силу тока, проходящего через реостат, изготовленный из никелиновой проволоки длиной 50 м и площадью поперечного сечения 1 мм2, если напряжение на зажимах реостата равно 45 В.
Задача № 10. Сопротивление проволоки, у которой площадь поперечного сечения 0,1 мм2, равно 180 Ом. Какой площади поперечного сечения надо взять проволоку той же длины и из того же материала, чтобы получить сопротивление 36 Ом?
Урок физики 8 класс.
Тема: « Решение задач на расчёт
сопротивления проводника, длины проводника, силы тока и напряжения»
Цель урока: научить учащихся решать задачи по изученной теме: «Закон Ома.
Расчет сопротивления. Удельное сопротивление»
Ход урока.
I. Организационный момент – 1 мин
II. Фронтальный опрос (вопросы к
опросу)
А) Как формулируется закон Ома?
Б) Как выразить напряжение на участка цепи, зная силу тока
в нём и его сопротивление?
В) Как зависит сопротивление проводника от его длины и от
площади поперечнего сечения?
Г) Что называется удельным сопротивлением проводника?
Д) По какой формуле можно рассчитыват удельное сопротивление
проводника?
III.
Решение
задач.
Задача 1.
Сопротивление
проводника 70 Ом, сила тока в нем 6 мА. Каково напряжение на его концах?
![]() Дано: Решение.
Дано: Решение.
R= 70 Ом U = I · R
![]() I = 6 мА
I = 6 мА
= 0,006 A
U
= 0,006 А· 70 Ом = 0, 42 В.
U = ?
Ответ: U = 0, 42 В.
Задача 2.
Найдите сопротивление спирали, сила тока в
которой 0,5 А, а напряжение на её концах 120 В.
![]() Дано: Решение.
Дано: Решение.
U = 120 B R![]()
![]() I =
I =
0,5 A
R
= ![]()
R =
? Ответ: R
= 240 Ом.
Задача 3.
Сопротивление нагревательного элемента
утюга 88 Ом, напряжение в электросети 220 В. Какова сила тока в
нагревательном элементе?
![]() Дано: Решение.
Дано: Решение.
R= 88 Ом ![]()
![]() U = 220
U = 220
B I =![]() = 2,5 А
= 2,5 А
I = ? Ответ:
I = 2,5 A.
Задача
4.
Определите сопротивление алюминиевого
провода длиной 100 м и площадью поперечного сечения 2,8 мм2.
![]() Дано: Решение.
Дано: Решение.
l = 100 м R = ![]()
r = 0,028 ![]() R
R
= 0,028 ![]() ×
×![]() = 1 Ом
= 1 Ом
![]() S
S
=2, 8 мм2
R =
? Ответ: R
= 1 Ом.
Задача 5.
Рассчитайте удельное сопротивление меди,
провод из которой длиной 500 м и площадью поперечного сечения 0,1 мм2
имеет сопротивление
85 Ом.
![]() Дано: Решение.
Дано: Решение.
l = 500 м R = ![]()
R = 85 Ом
r
= R×S / l
S =0,1мм2
r
= 85 Ом× 0,1мм2/500 м =1,7×10-2
Ом×мм2 / м
![]()
r =
? Ответ: r
= 0,017 Ом×мм2 / м
Задача 6.
Найти площадь поперечнего сечения
алюминевого праовода длиной 500 м, имеющего сопротивление 7 Ом.
![]() Дано: Решение.
Дано: Решение.
l
= 500 м R = ![]()
R = 7 Ом
S
= r×l
/ R
r = 0,027Ом ×мм2
/ м S = 0,027Ом ×мм2
/ м× 500 м / 7 Ом = 1,93 мм2
![]()
S
=? Ответ:S »2
мм2
Задача 7.
Какова сила тока на участке цепи,
состоящей из константовой проволки длиной 10 м и сечением 1,2 мм2,
если напряжение на концах этого участка равно 20 В?
![]() Дано: Решение.
Дано: Решение.
l
= 10 м
R = ![]()
U = 20 B
I
= U/R
r = 0,5 Ом ×мм2
/ м =0,5 ×10-6м2 R
= 0,5 ×10-6м2×
10 м/1,2×10-6 м2 =50/12
![]() S = 1,2 мм2
S = 1,2 мм2
= 1,2×10-6 м2
I =20 B×12/50
Ом
=4,8 А
I
=? Ответ:
I
=4, 8 A.
Задача 8.
Чему равна длина железного провода,
имеющего площадь поперечнего сечения 0,8мм2, если при прохождении по
нему тока 1 А напряжение на его концах равно 12 В?
Дано:
Решение.
![]() I
I
= 1А
R = ![]() ;
; ![]()
U = 12 B
R=
U/I
r = 0,1 Ом ×мм2
/ м =0,1 ×10-6 Ом×м
R
= ![]() =12 Ом.
=12 Ом.
![]() S = 0,8 мм2
S = 0,8 мм2
= 0,8×10-6 м2
 = 96 м
= 96 м
l
= ? Ответ: ![]() = 96 м.
= 96 м.
Задача 9
Рассчитайте напряжение на концах
линии электропередачи длиной 0,5 км при силе тока в ней 15 А , если провода,
изготовлены из алюминия, имеют площадь поперечнего сечения 14 мм2.
Дано:
Решение.
![]() I
I
= 15А
I
=![]() ; U
; U
= I× R
r = 0,28 ×10-7
Ом×м
R = ![]() ;
;
S
= 14 мм2 = 14×10-6 м2
![]() R
R
= 0, 28 ×10-7 Ом×м×
500 м/ 14×10-6 м2=
![]() l
l
= 0, 5 км = 500 м = 1 Ом.
U
=? U
= 15A×1
Ом =15 В
Ответ:
U=
15B.
Задача 10.
Определите силу тока, проходящего через
реостат, изготовленный из никелиневой проволки длиной 25 м и площадью
поперечнего сечения 0,5 мм2, если напряжение на зажимах реостата
равно 45 В.
![]() Дано: Решение.
Дано: Решение.
l
= 25 м
R = ![]()
U = 45B I = U/R
r = 0,4 ×10-6м2
R = 0,4 ×10-6м2×
25 м/0,5×10-6
м2
=20 Ом
![]() S = 0, 5 мм2
S = 0, 5 мм2
= 0,5×10-6 м2
I =45 B×/
20 Ом =2,25 А
I
=? Ответ:
I
=2, 25 A.
Задача 11.
Допустимый ток для изолированного медного
провода сечением
1 мм2 при продолжительной
работе равен 11 А. Сколько метров такой проволки можно включить в сеть с
напряжением 220 В?
Дано:
Решение.
![]() I
I
= 11А
R = ![]() ;
; ![]()
U = 220 B
R= U/I
r = 0,17 ×10-7
Ом×м
R = ![]() =20 Ом.
=20 Ом.
![]() S = 1 мм2
S = 1 мм2
= 10-6 м2
 = 1176,5 м
= 1176,5 м
l
= ? Ответ: ![]() = 1176,5м.
= 1176,5м.
Задача 12.
Определите напряжение на концах железого
провода длиной 140 см и площадью поперечнего сечения 0,2 мм2, по
которому течет ток 250 мА.
Дано:
Решение.
![]() I
I
= 250 мА =0,25А
I
=![]() ; U
; U
= I× R
r = 0, 1 ×10-6
Ом×м
R = ![]() ;
;
S
= 2 мм2 = 2×10-6 м2
![]() R
R
= 0,1 ×10-6 Ом×м×
1,4 м/ 2×10-6 м2
=
![]() l
l
= 140 см = 1, 4 м = 0, 07
Ом.
U
=? U
= 0,25A×0,
07 Ом =0,0175 В
Ответ: U=
17, 5 мB.
IV.Итоги
урока.
V.
На дом повторение §§§
40-46.Упражнение 30(2;3) по учебнику
Перышкин А. В.
2013год
Литература. Е.А.
Марон
«Физика опорные
конспекты и разноуровневые задания»
