Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 1 декабря 2022 года; проверки требуют 10 правок.
| Механика сплошных сред |
|---|
 |
| Сплошная среда |
|
Классическая механика Закон сохранения массы · Закон сохранения импульса |
|
Теория упругости Напряжение · Тензор · Твёрдые тела · Упругость · Пластичность · Закон Гука · Реология · Вязкоупругость |
|
Гидродинамика Жидкость · Гидростатика · Гидродинамика · Вязкость · Ньютоновская жидкость · Неньютоновская жидкость · Поверхностное натяжение |
|
Основные уравнения Уравнение непрерывности · Уравнение Эйлера · Уравнение Громеки — Лэмба · Уравнение Бернулли · Уравнения Навье — Стокса · Уравнение вихря · Уравнение диффузии · Закон Гука |
| См. также: Портал:Физика |
Зако́н Гу́ка — утверждение, согласно которому деформация, возникающая в упругом теле (пружине, стержне, консоли, балке и т. д.), прямо пропорциональна силе упругости, возникающей в этом теле. Открыт в 1660 году английским учёным Робертом Гуком[1].
Закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности связь между силой и деформацией становится нелинейной. Для многих сред закон Гука неприменим даже при малых деформациях.
Закон Гука для тонкого стержня[править | править код]
Для тонкого растяжимого стержня закон Гука имеет вид:
Здесь 


Коэффициент упругости зависит как от свойств материала, так и от размеров стержня. Можно выделить зависимость от размеров стержня (площади поперечного сечения 

Величина 
Если ввести относительное удлинение
и нормальное напряжение в поперечном сечении
то закон Гука для относительных величин запишется как
В такой форме он справедлив для любых малых объёмов материала.
Также при расчёте прямых стержней применяют запись закона Гука в относительной форме
Закон Гука и измерение силы[править | править код]
Закон Гука лежит в основе измерения сил пружинным механическим динамометром[2]. В этом приборе измеряемая сила передаётся пружине, которая в зависимости от направления силы сжимается или растягивается. Величина упругой деформации пружины пропорциональна силе воздействия и регистрируется[3].
Принципиальная возможность измерения обеспечивается уже свойством упругости, но без закона Гука упомянутая пропорциональность отсутствовала бы и градуировочная шкала стала бы неравномерной, что неудобно.
Обобщённый закон Гука[править | править код]
В общем случае напряжения и деформации описываются тензорами второго ранга в трёхмерном пространстве (имеют по 9 компонент). Связывающий их тензор упругих постоянных является тензором четвёртого ранга 

где 


Благодаря симметрии тензоров напряжения и деформации, закон Гука может быть представлен в матричной форме.
Для линейно упругого изотропного тела:
где:
См. также[править | править код]
- Модуль Юнга
Примечания[править | править код]
- ↑ Гука закон. Статья в физической энциклопедии. Дата обращения: 2 декабря 2015. Архивировано 2 октября 2015 года.
- ↑ Б. М. Яворский, А. А. Детлаф. Справочник по физике. М.:Наука (1985). — см. на стр. 22, в парагр. 1.1.2 Сила: «…измерение сил с помощью пружинного динамометра основано на законе Гука…» Дата обращения: 10 декабря 2020. Архивировано 10 декабря 2020 года.
- ↑ Cм. статью «Динамометр» Архивная копия от 11 января 2022 на Wayback Machine в «Сельскохозяйственной энциклопедии», Т. 1 (А — Е), ред. коллегия: П. П. Лобанов (глав ред) [и др.] (1949)
Сила упругости. Закон Гука
- Виды деформаций
- Закон Гука
- Измерение силы с помощью динамометра
- Задачи
п.1. Виды деформаций
Под действием силы все тело или отдельные его части приходят в движение.
При движении одних частей тела относительно других происходит изменение формы и размеров.
Деформация – это изменение взаимного положения частиц тела, связанное с их перемещением друг относительно друга под действием приложенной силы, при котором тело изменяет свою форму и размеры.
 |
К простейшим видам деформации относятся:
|
Различают упругие (обратимые) и неупругие (необратимые) деформации.
Деформация является упругой, если, после прекращения действия вызвавших её сил, тело полностью восстанавливает свою форму и размеры.
Например, если немного согнуть школьную линейку, растянуть пружину или надавить на воздушный шарик, после прекращения действия силы линейка выпрямится, пружина сожмется, и шарик опять станет круглым. Эти деформации – упругие, они обратимы.
Если же приложенная сила окажется слишком большой, линейка сломается, пружина так и останется растянутой, а шарик лопнет. Эти деформации – неупругие, они необратимы.
Все здания и сооружения вокруг нас рассчитываются так, чтобы их «нагруженные» части испытывали только упругие деформации; это обеспечивает надёжность и долговечность конструкций.
Восстановление формы и размера тела при упругой деформации происходит под действием силы упругости, которая возникает благодаря межатомным и межмолекулярным взаимодействиям.

Сила упругости уравновешивает действие внешней силы и направлена в сторону, противоположную смещению частиц.
Например (см. рисунок):
- при растяжении сила упругости стремится сжать тело;
- при сжатии сила упругости стремится распрямить тело.
п.2. Закон Гука
 |
Проведем серию опытов с пружиной. Пусть при действии на пружину силой (F) мы получаем деформацию (удлинение) (Delta l). При этом в пружине возникают силы упругости, стремящиеся вернуть её в исходное положение, (overrightarrow{F_{text{упр}}}=-overrightarrow{F}). Если приложенную силу увеличить в 2 раза, то деформация также увеличится в 2 раза. Увеличение силы в 3 раза приводит к росту деформации в 3 раза и т.д. Опыты показывают, что во всех случаях деформация будет прямо пропорциональна приложенной силе. |
Следовательно, сила упругости также будет прямо пропорциональна деформации: $$ F_{text{упр}}simDelta l $$
Для каждого тела отношение силы упругости к величине деформации при малых упругих деформациях является постоянной величиной $$ k=frac{F_{text{упр}}}{Delta l}=const $$ которая называется коэффициентом упругости или жесткостью.
Жесткость тела зависит от формы, размеров и материала, из которого оно изготовлено.
В системе СИ жесткость измеряется в ньютонах на метр, (frac{text{Н}}{text{м}}).
Закон Гука
Сила упругости, возникающая во время упругой деформации тела, прямо пропорциональна удлинению (величине деформации): $$ F_{text{упр}}=kDelta l $$ Сила упругости всегда направлена противоположно деформации.
п.3. Измерение силы с помощью динамометра
 |
Динамометр– это прибор для измерения силы.
Простейший пружинный динамометр состоит из пружины с крючком и дощечки со шкалой (проградуированной в ньютонах). |
В технике используются динамометры более сложных конструкций.
Но принцип действия – использование закона Гука – во многих из них сохраняется.
п.4. Задачи
Задача 1. Резиновая лента удлинилась на 10 см под действием силы 50 Н. Какова жесткость ленты?
Дано:
(Delta l=10 text{см}=0,1 text{м})
(F=50 text{Н})
__________________
(k-?)
Жесткость ленты $$ k=frac{F}{Delta l} $$ $$ k=frac{50}{0,1}=500 left(frac{text{Н}}{text{м}}right) $$ Ответ: 500 Н/м
Задача 2. Под действием силы 300 Н пружина динамометра удлинилась на 0,6 см. Каким будет удлинение пружины под действием силы 700 Н? Ответ запишите в миллиметрах.
Дано:
(F_1=300 text{Н})
(Delta l_1=0,6 text{см}=6cdot 10^{-3} text{м})
(F_2=700 text{Н})
__________________
(Delta l_2-?)
Жесткость пружины begin{gather*} k=frac{F_1}{Delta l_1}=frac{F_2}{Delta l_2}Rightarrow Delta l_2=frac{F_2}{F_1}Delta l_1\[6pt] Delta l_2=frac{700}{300}cdot 6cdot 10^{-3}=14cdot 10^{-3} (text{м})=14 (text{мм}) end{gather*} Ответ: 14 мм
Задача 3. Пружина без груза имеет длину 30 см и коэффициент жесткости 20 Н/м. Найдите длину растянутой пружины, если на нее действует сила 5 Н. Ответ запишите в сантиметрах.
Дано:
(l_0=30 text{cм}=0,3 text{м})
(k=20 text{Н/м})
(F=5 text{Н})
__________________
(l-?)
Удлинение пружины под действием силы: $$ Delta l=frac Fk $$ Длина растянутой пружины begin{gather*} l=l_0+Delta l=l_0+frac Fk\[6pt] l=0,3+frac{5}{20}=0,3+0,25=0,55 (text{м})=55 (text{cм}) end{gather*} Ответ: 55 cм
Задача 4*. Грузовик взял на буксир легковой автомобиль массой 1,5 т с помощью троса. Двигаясь равноускоренно, они проехали путь 600 м за 50 с. На сколько миллиметров удлинился во время движения трос, если его жесткость равна (3cdot 10^5 text{Н/м})?
Дано:
(m=1,5 text{т}=1500 text{кг})
(s=600 text{м})
(t=50 text{c})
(v_0=0)
(k=3cdot 10^5 text{Н/м})
__________________
(Delta l-?)
Сила упругости, возникающая в тросе, уравновешивает силу тяги, передвигающую автомобиль с постоянным ускорением: $$ F_{text{упр}}=kDelta l=F_{text{т}}=ma $$ Перемещение из состояния покоя $$ s=frac{at^2}{2}Rightarrow a=frac{2s}{t^2} $$ Получаем: begin{gather*} kDelta l=mcdotfrac{2s}{t^2}Rightarrow Delta l=frac mkcdot frac{2s}{t^2}\[6pt] Delta l=frac{1500}{3cdot 10^5}cdot frac{2cdot 600}{50^2}=2,4cdot 10^{-3} (text{м})=2,4 (text{мм}) end{gather*} Ответ: 2,4 мм
Закон
Гука–
уравнение теории упругости, связывающее
напряжение и деформацию упругой среды.
Дельта L=FL/ES,
где дельта L-абсолютное
удлинение, L-длина
образца, F-сила
растяжения, E-модуль
упругости, S-площадь
образца.
Модуль
Юнга Е (модуль упругости) –
физическая величина, характеризующая
свойства материала сопротивляться
растяжению/сжатию при упругой деформации;
отношение напряжения, возникающего при
растяжении тела, к удлинению, вызванному
этим напряжением.
Модуль
Юнга рассчитывается следующим образом:
![]()
где:![]()
E — модуль
упругости
F — сила
S —
площадь поверхности, по которой
распределено действие силы,
l —
длина деформируемого стержня,
x —
модуль изменения длины стержня в
результате упругой деформации (измеренного
в тех же единицах, что и длина l).
15.
з-он Ома
Если
ток является синусоидальным с циклической
частотой ω, а цепь содержит не только
активные, но и реактивные компоненты
(ёмкости, индуктивности), то закон Ома
обобщается; величины, входящие в него,
становятся комплексными:
![]()
где:
U
= U0eiωt — напряжение или разность
потенциалов,
I
— сила тока,
Z
= Re−iδ — комплексное сопротивление
(импеданс),
R
= (Ra2 + Rr2)1/2 — полное сопротивление,
Rr
= ωL − 1/(ωC) — реактивное сопротивление
(разность индуктивного и емкостного),
Rа
— активное (омическое) сопротивление,
не зависящее от частоты,
δ
= − arctg (Rr/Ra) — сдвиг фаз между напряжением
и силой тока.
Реактивное
сопротивление – это сопротивление
катушек индуктивности (дросселей) и
конденсаторов. Величина реактивного
сопротивления уже зависит от частоты
тока. Так на постоянном токе реактивное
сопротивление конденсатора устремляется
к бесконечности, а дросселя наоборот –
к нулю (без учета активной составляющей
сопротивления провода).
С
изменением частоты тока электрическое
сопротивление конденсатора изменяется,
по закону:
Xc
= 1/2pfC2
где
Xc – сопротивление, Ом; f – частота, Гц;
С – емкость, Ф.
Электрическое
сопротивление конденсатора переменному
току можно измерить. Зная сопротивление
и частоту тока, легко по формуле вычислить
емкость. Кроме того, если в электрической
цепи стоит конденсатор происходит сдвиг
фаз напряжения и тока. Причем ток
опережает напряжение на величину 90°.
Реактивное
сопротивление катушки индуктивности
с увеличением частоты возрастает:
XL
= 2pfL
где
XL – сопротивление катушки, Ом; f –
частота, Гц; L – индуктивность, Гн.
Индуктивность
дросселя легко вычисляется по известному
сопротивлению и заданной частоте тока.
При этом фазы напряжения и тока на
катушке индуктивности сдвигаются
относительно друг друга, и теперь ток
отстает от напряжения на 90°.
Для
измерения реактивного сопротивления
емкости и индуктивности потребуется,
прежде всего, переменный ток синусоидальной
формы. С задачей программного генератора
с легкостью может справиться звуковая
плата компьютера. Другая проблема –
определение величины электрического
сопротивления измеряемого элемента.
Но оказывается и эту задачу можно решить
программным путем, с помощью той же
звуковой платы, не прибегая к специальным
аналого-цифровым преобразователям
16.
Электрический диполь
Электрический
диполь. Система
состоящая из 2 равных противоположных
по знаку точечных эл зарядов расположенных
на нек расстоянии друг от друга(плечо
диполя) основная хар. Дипольный момент
p=ql. Диполь Явл источником поля. Потенциал
в точке удаленной от зарядов на расстоянии
r и r1![]()
Если
диполь эл момент которого p в точке
равноудаленной от эл диполя то плечо
диполя мало. Разность потенциалов 2
точек поля и диполя зависит от синуса
половинного угла под которым видны эти
точки и проекции эл момента диполя
напрямую соед эти точки. Yв-Yа=1/4пEE0 * p/r2
*2син
бетта/2* cosальфа.
17.
Токовый монополь
Токовый
монополь- единичный источник электрического
потенциала. Вывод формулы потенциала
поля токового монополя в бесконечно
проводящей среде:j=
– 1/π * dφ(
«фи»)/ dr
Где
j-
плотность электрического поля Р(пи)
–удельное сопротивление среды, r-
расстояние до униполя.
Токовый
диполь- это совокупность двух равных
по абсолютной величине разноимённых
точечных зарядов, находящихся на
некотором расстоянии друг от друга.
Потенциал
поля убывает на значительных расстояниях
r
от него пропорционально 1/r(в
степени l),
l=1,
значит конечная формула равна 1/r(в
квадрате).
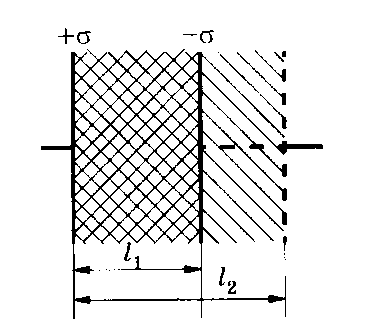
Электрическое
поле токового диполя:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Закон Гука, теория и онлайн калькуляторы
Закон Гука
Если на тело воздействовать некоторой силой, то его размер и (или) форма изменяются. Это процесс называют деформацией тела. В телах, подвергающихся деформациям,
возникают силы упругости, уравновешивающие внешние силы.
Виды деформации
Все деформации можно разделить на два вида: упругие деформации и пластические.
Определение
Упругой называют деформацию, если после снятия нагрузки прежние размеры тела и его форма полностью восстанавливаются.
Определение
Пластической считают деформацию, при которой появившиеся, вследствие деформации, изменения размера и формы тела, после снятия
нагрузки восстанавливаются частично.
Характер деформации зависит от
- величины и времени воздействия внешней нагрузки;
- материала тела;
- состояния тела (температуры, способов обработки и т.д).
Резкой границы между упругой и пластической деформациями не существует. В большом числе случаев малые и кратковременные деформации можно считать упругими.
Формулировки закона Гука
Эмпирически получено, что чем большую деформацию необходимо получить, тем большую деформирующую силу следует приложить к телу. По величине деформации ($Delta l$)
можно судить о величине силы:
[Delta l=frac{F}{k}left(1right),]
выражение (1) означает, что абсолютная величина упругой деформации прямо пропорциональная приложенной силе. Данное утверждение является содержанием закона Гука.
При деформации удлинения (сжатия) тела выполняется равенство:
[F=kleft(l-l_0right)=kDelta l left(2right),]
где $F$ – деформирующая сила; $l_0$ – начальная длина тела; $l$ – длина тела после деформации; $k$ – коэффициент упругости (коэффициент жесткости, жесткость), $
left[kright]=frac{Н}{м}$. Коэффициент упругости зависит от материала тела, его размеров и формы.
Так как в деформированном теле возникают силы упругости ($F_u$), которые стремятся восстановить прежние размеры и форму телу, то часто закон Гука формулируют
относительно сил упругости:
[F_u=kleft|Delta lright| left(3right).]
Закон Гука хорошо работает для деформаций, которые возникают в стержнях из стали, чугуна, и других твердых веществ, в пружинах. Справедлив закон Гука для деформаций
растяжения и сжатия.
Закон Гука для малых деформаций
Сила упругости зависит от изменения расстояния между частями одного и того же тела. Следует помнить, что закон Гука выполняется только для малых деформаций. При
больших деформациях сила упругости не пропорциональна измерению длины, при дальнейшем увеличении деформирующего воздействия тело способно разрушаться.
Если деформации тела малы, то силы упругости можно определять по ускорению, которое данные силы сообщают телам. Если тело неподвижно, то модуль силы упругости
находят из равенства нулю векторной суммы сил, которые действуют на тело.
Закон Гука можно записывать не только относительно сил, но часто его формулируют для такой величины как напряжение ($sigma =frac{F}{S}$ – сила, которая действует
на единичную площадь поперечного сечения тела), тогда для малых деформаций:
[sigma =Еfrac{Delta l}{l} left(4right),]
где $Е$ – модуль Юнга;$ frac{Delta l}{l}$ – относительное удлинение тела.
Примеры задач с решением
Пример 1
Задание. К стальному тросу длинной $l$, диаметром $d$ подвесили груз массой $m$. Каково напряжение в тросе ($sigma $), а также
абсолютное его удлинение ($Delta l$)?
Решение. Сделаем рисунок.
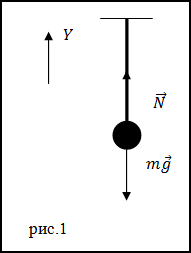
Для того чтобы найти силу упругости, рассмотрим силы, которые действуют на тело, подвешенное к тросу, так как сила
упругости будет равна по величине силе натяжения ($overline{N}$). По второму закону Ньютона имеем:
[moverline{g}+overline{N}=0 left(1.1right).]
В проекции на ось Y уравнения (1.1) получим:
[N=mg left(1.2right).]
По третьему закону Ньютона тело, действует на трос с силой равной по величине силе $overline{N}$, трос, действует на тело с силой $overline{F}$,
равной$overline{ N,}$ но противоположного направления, так деформирующая трос сила ($overline{F}$) равна:
[overline{F}=-overline{N }left(1.3right).]
Под воздействием деформирующей силы в тросе возникает сила упругости, которая равна по величине:
[F_u=N=mgleft(1.4right).]
Напряжение в тросе ($sigma $) найдем как:
[sigma =frac{F_u}{S}=frac{mg}{S}left(1.5right).]
Площадь S – это площадь поперечного сечения троса:
[S=pi frac{d^2}{4}left(1.6right).]
Получим:
[sigma =frac{4mg }{{pi d}^2}left(1.7right).]
По закону Гука:
[sigma =Еfrac{Delta l}{l}left(1.8right),]
значит:
[frac{Delta l}{l}=frac{sigma }{E}to Delta l=frac{sigma l}{E}to Delta l=frac{4mgl }{{pi d}^2E}.]
Ответ. $sigma =frac{4mg }{{pi d}^2}; Delta l=frac{4mgl }{{pi d}^2E}$
Пример 2
Задание. Какова абсолютная деформация первой пружины из двух последовательно соединенных пружин (рис.2), если коэффициенты
жесткости пружин равны: $k_1 и k_2$, а удлинение второй пружины составляет $Delta x_2$?
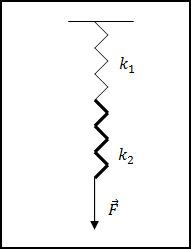
Решение. Если система из последовательно соединенных пружин находится в состоянии равновесия, то силы натяжения данных пружин
одинаковы:
[F_1=F_2=F left(2.1right).]
По закону Гука:
[F_1=k_1Delta x_1;; F_2=k_2Delta x_2left(2.2right).]
Согласно (2.1) и (2.2) имеем:
[k_1Delta x_1=k_2Delta x_2 left(2.3right).]
Выразим из (2.3) удлинение первой пружины:
[Delta x_1=frac{k_2Delta x_2}{k_1}.]
Ответ. $Delta x_1=frac{k_2Delta x_2}{k_1}$.
Читать дальше: закон Паскаля.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Сила упругости широко используется в технике. Эта сила возникает в упругих телах при их деформации. Деформация – это изменение формы тела, под действием приложенных сил.
Виды деформации
Деформация – это изменение формы, или размеров тела.
Есть несколько видов деформации:
- сдвиг;
- кручение;
- изгиб;
- сжатие/растяжение;
Деформация сдвига возникает, когда одни части тела сдвигаются относительно других его частей. Если подействовать на верхнюю часть картонного ящика, наполненного различными предметами, горизонтальной силой, то вызовем сдвиг верхней части ящика относительно его нижней части.
Сжатие или растяжение легко представить на примере прямоугольного куска тонкой резины. Такая деформация используется, к примеру, в резинках для одежды.
Примеры изгиба и кручения показаны на рисунке 1. Пластиковая линейка, деформированная изгибом, представлена на рис. 1а, а на рисунке 1б – эта же линейка, деформируемая кручением.

Рис. 1. пластиковая линейка, деформированная изгибом – а) и кручением – б)
В деформируемом теле возникают силы, имеющие электромагнитную природу и препятствующие деформации.
Растяжение пружины
Рассмотрим подробнее деформацию растяжения на примере пружины.
Давайте прикрепим пружину к некоторой поверхности (рис. 2). На рисунке слева указана начальная длина (L_{0}) пружины.

Рис. 2. Сравнивая длину свободной пружины с длиной нагруженной, можно найти ее удлинение
Подвесим теперь к пружине груз. Пружина будет иметь длину (L), указанную на рисунке справа.
Сравним длину нагруженной пружины с длиной свободно висящей пружины.
[ large L_{0} + Delta L = L ]
Найдем разницу (разность) между длинами свободно висящей пружины и пружины с грузом. Вычтем для этого из обеих частей этого уравнения величину (L_{0}).
[ large boxed{ Delta L = L — L_{0} }]
( L_{0} left(text{м} right) ) – начальная длина пружины;
( L left(text{м} right) ) – конечная длина растянутой пружины;
( Delta L left(text{м} right) ) – кусочек длины, на который растянули пружину;
Величину ( Delta L ) называют удлинением пружины.
Иногда рассчитывают относительное удлинение. Это относительное удлинение часто выражают десятичной дробью. Или дробью, в знаменателе которой находится число 100 — такую дробь называют процентом.
Примечание: Отношение – это дробь. Относительное – значит, дробное.
[ large boxed{ frac{Delta L }{ L_{0}} = frac{ L — L_{0}}{L_{0} } = varepsilon } ]
( varepsilon ) – это отношение (доля) растяжения пружины к ее начальной длине. Измеряют в процентах и называют относительным удлинением.
Расчет силы упругости
Если растягивать пружину вручную, мы можем заметить: чем больше мы растягиваем пружину, тем сильнее она сопротивляется.
Значит, с удлинением пружины связана сила, которая сопротивляется этому удлинению.
Конечно, если пружина окажется достаточно упругой, чтобы сопротивляться. Например, разноцветная пружина-игрушка (рис. 3), изготовленная из пластмассы, сопротивляться растяжению, увеличивающему ее длину в два раза, практически не будет.

Разноцветная пластмассовая пружина-игрушка растяжению сопротивляется слабо
Закон Гука
Английский физик Роберт Гук, живший во второй половине 17-го века, установил, что сила сопротивления пружины и ее удлинение связаны прямой пропорциональностью. Силу, с которой пружина сопротивляется деформации, он назвал ( F_{text{упр}} ) силой упругости.
[ large boxed{ F_{text{упр}} = k cdot Delta L }]
Эту формулу назвали законом упругости Гука.
( F_{text{упр}} left( H right) ) – сила упругости;
( Delta L left(text{м} right) ) – удлинение пружины;
( displaystyle k left(frac{H}{text{м}} right) ) – коэффициент жесткости (упругости).
Какие деформации называют малыми
Закон Гука применяют для малых удлинений (деформаций).
Если убрать деформирующую силу и тело вернется к первоначальной форме (размерам), то деформации называют малыми.
Если же тело к первоначальной форме не вернется – малыми деформации назвать не получится.
Как рассчитать коэффициент жесткости
Груз, прикрепленный к концу пружины, растягивает ее (рис. 4). Измерим удлинение пружины и составим силовое уравнение для проекции сил на вертикальную ось. Вес груза направлен против оси, а сила упругости, противодействующая ему – по оси.

Рис. 4. Вес подвешенного на пружине груза уравновешивается силой упругости
Так как силы взаимно компенсируются, в правой части уравнения находится ноль.
[ large F_{text{упр}} — m cdot g = 0 ]
Подставим в это уравнение выражение для силы упругости
[ large k cdot Delta L — m cdot g = 0 ]
Прибавим к обеим частям вес груза и разделим на измеренное изменение длины (Delta L ) пружины. Получим выражение для коэффициента жесткости:
[ large boxed{ k = frac{ m cdot g }{Delta L} }]
(g) – ускорение свободного падения, оно связано с силой тяжести.
Соединяем две одинаковые пружины
В задачниках по физике и пособиях для подготовки к ЕГЭ встречаются задачи, в которых одинаковые пружины соединяют последовательно, либо параллельно.
Параллельное соединение пружин
На рисунке 5а представлена свободно висящая пружина. Нагрузим ее (рис. 5б), она растянется на величину (Delta L). Соединим две такие пружины параллельно и подвесим груз в середине перекладины (рис. 5в). Из рисунка видно, что конструкция из двух параллельных пружин под действием груза растянется меньше, нежели единственная такая пружина.

Рис. 5. Две пружины, соединенные параллельно, деформируются меньше одной такой пружины
Сравним растяжение двух одинаковых пружин, соединенных параллельно, с растяжением одной пружины. К пружинам подвешиваем один груз весом (mg).
Одна пружина:
[ large k_{1} cdot Delta L = m cdot g ]
Две параллельные пружины:
[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= m cdot g ]
Так как правые части уравнений совпадают, левые части тоже будут равны:
[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= k_{1} cdot Delta L ]
Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:
[ large k_{text{параллел}} cdot frac{1}{2}= k_{1} ]
Умножим обе части полученного уравнения на число 2:
[ large boxed{ k_{text{параллел}} = 2k_{1} } ]
Коэффициент жесткости (k_{text{параллел}}) двух пружин, соединенных параллельно, увеличился вдвое, в сравнении с одной такой пружиной
Последовательное соединение пружин
Рисунок 6а иллюстрирует свободно висящую пружину. Нагруженная пружина (рис. 6б), растянута на длину (Delta L). Теперь возьмем две такие пружины и соединим их последовательно. Подвесим груз к этим (рис. 6в) пружинам.
Практика показывает, что конструкция из двух последовательно соединенных пружин под действием груза растянется больше единственной пружины.
На каждую пружину в цепочке действует вес груза. Под действием веса пружина растягивается и передает далее по цепочке этот вес без изменений. Он растягивает следующую пружину. А та, в свою очередь, растягивается на такую же величину (Delta L).
Примечание: Под действием силы пружина растягивается и передает эту растягивающую силу далее по цепочке без изменений

Рис. 6. Система, состоящая из двух одинаковых пружин, соединенных последовательно, деформируются больше одной пружины
Сравним растяжение двух одинаковых последовательно соединенных пружин и растяжение единственной пружины. В обоих случаях к пружинам подвешиваем одинаковый груз весом (mg).
Одна пружина:
[ large k_{1} cdot Delta L = m cdot g ]
Две последовательные пружины:
[ large k_{text{послед}} cdot Delta L cdot 2 = m cdot g ]
Так как правые части уравнений совпадают, левые части тоже будут равны:
[ large k_{text{послед}} cdot Delta L cdot 2 = k_{1} cdot Delta L ]
Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:
[ large k_{text{послед}} cdot 2 = k_{1} ]
Разделим обе части полученного уравнения на число 2:
[ large boxed{ k_{text{послед}} = frac{k_{1}}{2} } ]
Коэффициент жесткости (k_{text{послед}}) двух пружин, соединенных последовательно, уменьшится вдвое, в сравнении с одной такой пружиной
Потенциальная энергия сжатой или растянутой пружины
Пружина сжатая (левая часть рис. 7), или растянутая (правая часть рис. 7) на длину (Delta L ) обладает потенциальной возможностью вернуться в первоначальное состояние и при этом совершить работу, например, по перемещению груза. В таких случаях физики говорят, что пружина обладает потенциальной энергией.

Рис. 7. Деформированная — сжатая или растянутая пружина обладает потенциальной энергией
Эта энергия зависит от коэффициента жесткости пружины и от ее удлинения (или укорочения при сжатии).
Чем больше жесткость (упругость) пружины, тем больше ее потенциальная энергия. Увеличив удлинение пружины получим повышение ее потенциальной энергии по квадратичному закону:
[ large boxed{ E_{p} = frac{k}{2} cdot left( Delta L right)^{2} }]
( E_{p} left( text{Дж} right)) – потенциальная энергия сжатой или растянутой пружины;
( Delta L left(text{м} right) ) – удлинение пружины;
( displaystyle k left(frac{H}{text{м}} right) ) – коэффициент жесткости (упругости) пружины.
Выводы
- Упругие тела – такие, которые сопротивляются деформации;
- Во время деформации в упругих телах возникает сила, она препятствует деформации, ее называют силой упругости;
- Деформация – изменение формы, или размеров тела;
- Есть несколько видов деформации: изгиб, кручение, сдвиг, растяжение/сжатие;
- Удлинение пружины – это разность ее конечной и начальной длин;
- Сжатая или растянутая пружина обладает потенциальной энергией (вообще, любое упруго деформированное тело обладает потенциальной энергией);
- Система, состоящая из нескольких одинаковых пружин, будет иметь коэффициент жесткости, отличный от жесткости единственной пружины;
- Если пружины соединяют параллельно – коэффициент жесткости системы увеличивается;
- А если соединить пружины последовательно – коэффициент жесткости системы уменьшится.













