«Не знаешь Ома – сиди дома» — пословица старых электриков. Действительно, этот закон очень важен для понимания того, как связаны напряжение, ток и сопротивление, или проще говоря — от чего зависит ток и мощность нагрузки и как их рассчитать.
Для понимания этих базовых вещей нужно знать закон Ома для участка цепи и закон Ома для полной цепи. Главное различие между ними, что первый распространяется на отдельный участок или элемент и учитывает только его сопротивление и приложенное к нему напряжение, а второй учитывает и внутреннее сопротивление источника питания. Давайте разберёмся подробнее.
Закон Ома для участка цепи
Самый простой и всем известный со школы вариант — закон Ома для участка цепи. Его определение звучит следующим образом:
В виде формулы это выглядит так:
I=U/R,
где I — ток, U — напряжение, R— сопротивление.
То есть чтобы определить силу тока нужно знать напряжение на участке цепи (на элементе) и его сопротивление.
Напряжение на элементе равно произведению тока на сопротивление, то есть чтобы найти напряжение нужно знать ток в участке цепи и его сопротивление:
U=IR
Чтобы найти сопротивление по закону Ома, нужно знать напряжение и ток:
R=U/I
К сведению: правильнее говорить «падение напряжения», но для упрощения в разговорной речи говорят просто «напряжение на элементе» или «… на участке цепи».
Электрическое сопротивление измеряется в Омах, величина 1 Ом выражает такое сопротивление проводника, при котором по нему будет протекать ток в 1 ампер, если к нему приложить напряжение в 1 вольт.
Как запомнить эти формулы?
В виде формулы это выглядит так:
I=U/R,
где I — ток, U — напряжение, R— сопротивление.
То есть чтобы определить силу тока нужно знать напряжение на участке цепи (на элементе) и его сопротивление.
Напряжение на элементе равно произведению тока на сопротивление, то есть чтобы найти напряжение нужно знать ток в участке цепи и его сопротивление:
U=IR
Чтобы найти сопротивление по закону Ома, нужно знать напряжение и ток:
R=U/I
К сведению: правильнее говорить «падение напряжения», но для упрощения в разговорной речи говорят просто «напряжение на элементе» или «… на участке цепи».
Электрическое сопротивление измеряется в Омах, величина 1 Ом выражает такое сопротивление проводника, при котором по нему будет протекать ток в 1 ампер, если к нему приложить напряжение в 1 вольт.
Как запомнить эти формулы?
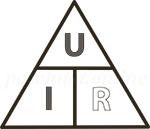
Для запоминания формул закона Ома есть удобная мнемоническая подсказка так называемый «треугольник Ома». В нём сверху размещена буква U, а снизу I и R. Как несложно догадаться, они обозначают напряжение, ток и сопротивление соответственно.
Для запоминания формул закона Ома есть удобная мнемоническая подсказка так называемый «треугольник Ома». В нём сверху размещена буква U, а снизу I и R. Как несложно догадаться, они обозначают напряжение, ток и сопротивление соответственно.
Как пользоваться треугольником? Всё просто — закройте пальцем величину, которую нужно найти, а оставшиеся не закрытыми буквы нужно умножить или разделить друг на друга, что подробно проиллюстрировано ниже.
Есть еще одна шпаргалка в виде круга разделенного на сегменты, где перечислены все необходимые формулы, кроме перечисленных выше, добавлены и формулы для вычисления мощности.
Примеры
Итак, чтобы научиться рассчитывать напряжение на участке цепи, решим простенькую задачу. У нас есть цепь, состоящая из 3 резисторов и идеального источника с напряжением 12В постоянного тока. Пусть участком цепи у нас будет резистор R2, найдём напряжение на нём.
Дано:
U= 12 В;
R1= 1 кОм;
R2= 2 кОм;
R3= 3 кОм;
Найти:
I — ?;
U(R2) — ?;
По закону Ома чтобы найти напряжение нужно знать ток через участок цепи и его сопротивление.
U=IR
Последнее у нас известно, поэтому нужно найти ток в цепи, элементы соединены последовательно, поэтому ток через каждый из них одинаков, и чтобы найти его силу — нужно сначала найти общее сопротивление всех элементов, но сначала переведём его в Омы:
R1 = 1 кОм = 1000 Ом; R2 = 2 кОм = 2000 Ом; R3 = 3 кОм = 3000 Ом.
Теперь найдём общее сопротивление:
Rобщ=R1+R2+R3=1000+2000+3000= 6000 Ом
Тогда ток в цепи равен:
I= U/R = 12/6000 = 0,002 А
И наконец падение напряжения на резисторе R2:
U(R2) = I*U(R2) = 0,002*2000=4В
Итого, на выводах резистора R2 будет 4 вольта.
Закон Ома для полной цепи
Определение закона Ома для полной цепи вы видите ниже, жирным выделено основное отличие от закона для участка цепи.
В формуле добавляется внутреннее сопротивление источника питания, а напряжение заменяется на ЭДС:
I=E/(R+r),
где I – ток, E – ЭДС, R – сопротивление, r- внутреннее сопротивление источника.
Внутреннее сопротивление источника обуславливается его устройством, например, сечением вторичной обмотки трансформатора, химическим составом, степенью заряда и состоянием электродов аккумуляторов и батареек и так далее. На схеме условно рисуется в виде резистора внутри источника, но на самом деле никакого «внутреннего» или «скрытого» сопротивления там нет, как было отмечено выше.
Почему важно учитывать внутреннее сопротивление источника? Всё очень просто — вы замечали, как погасают лампочки в автомобиле, когда стартер запускает двигатель? Это происходит из-за просадок на проводах и в аккумуляторе от высоких пусковых токов. В принципе, подобное мы наблюдаем, когда лампы накаливания «просаживаются» по яркости во время пуска мощной нагрузки, например, электродвигателей.
Примеры
Давайте проанализируем, как влияет внутреннее сопротивление источника на напряжение нагрузки. Допустим, что у нас есть какой-то источник с внутренним сопротивлением (r) в 1 Ом и ЭДС (E) в 12 Вольт. И есть 3 разных нагрузки, с сопротивлением (R) каждой из них: 10, 5 и 1 Ом соответственно. Нагрузку будем подключать по очереди, по одной для каждого расчета.
Рассчитаем ток первой нагрузки:
I1=E/(R1+r)=12/(10+1)=1.09 А
Рассчитаем напряжение на нагрузке:
U1=I1*R1=1.09*10=10.9 В
Сразу видим, что на нагрузке уже не 12, а 10 вольт, посчитаем другие варианты:
Рассчитаем ток второй нагрузки:
I2=E/(R2+r)=12/(5+1)=2 А
Рассчитаем напряжение на нагрузке:
U2=I2*R2=2*5=10 В
Рассчитаем ток третей нагрузки:
I3=E/(R3+r)=12/(1+1)=6 А
Рассчитаем напряжение:
U3=I3*R3=6*1=6 В
Как вы можете видеть на внутреннем сопротивлении падает какое-то напряжение, и падение напряжение прямо пропорционально току нагрузки. При этом до нагрузки доходит всё меньше и меньше напряжения.
Сделаем то же самое, но для источника с внутренним сопротивлением 0.1 Ома. Рассчитаем ток первой нагрузки:
I1=E/(R1+r)=12/(10+0,1)=1.18 А
Рассчитаем напряжение:
U1=I1*R1=1.18*10=11.8 В
Ток второй нагрузки:
I2=E/(R2+r)=12/(5+0,1)=2,35 А
Рассчитаем напряжение на нагрузке:
U2=I2*R2=2,35*5=11.75 В
Рассчитаем ток третей нагрузки:
I3=E/(R3+r)=12/(1+0,1)=10,9 А
Рассчитаем напряжение:
U3=I3*R3=10,9*1=10,9 В
Для удобства соберем все результаты расчётов в одну таблицу.
Из таблицы мы видим, что чем меньше внутреннее сопротивление источника — тем меньше просаживается напряжение под нагрузкой.
Заключение
Георг Симон Ом жил в 1786-1854 годах, в 1826 году вывел теоретически и подтвердил с помощью опытов закон выражающий связь напряжения, тока и сопротивления. Этот закон назвали в честь открывателя — законом Ома, а также единицу измерения электрического сопротивления.
Закон Ома — один из важнейших и основополагающих в электротехнике, он широко используется при расчетах электрических схем.
Пишите в комментариях, понравился ли вам такой формат теоретической статьи и какие статьи хотите увидеть в будущем?
Какие есть формулы для вычисления сопротивления резистора
Содержание
- 1 Что такое резистор
- 2 Сопротивление резистора
- 3 Последовательная цепь источника и сопротивлений
- 4 Параллельная схема элементов
- 5 Расчет смешанного соединения элементов схемы
- 6 Мощность рассеивания
- 7 Параметры резисторов
- 8 Определение параметров по маркировке и схеме
- 9 Видео по теме
Сопротивление направленному движению электронов (электрическому току) в проводах электроснабжения чаще всего провоцирует потери. Они зависят от площади сечения (S), длины (L), удельного сопротивления вещества провода (ρ). Однако, сопротивление послужило созданию самого распространенного элемента в электронике — резистора.
Что такое резистор
Деталь электрической или электронной схемы, сопротивляющаяся прохождению электрического тока, называется резистор (от латинского resisto — сопротивляюсь). Падение или изменение напряжения на этом элементе используется в схемотехнике для получения нужных процессов управления автоматикой или преобразования электричества в свет, тепло, звук или движение.
Наиболее удобно классифицировать резисторы по следующим признакам:
- назначение. Для различных сфер используют элементы с
общими свойствами или специфическими по частоте тока, точности изготовления или ограничения по напряжению;
- способ управления сопротивлением. Постоянные резисторы в определенном диапазоне напряжения и тока не меняют сопротивление. У переменных можно менять вручную данный параметр с целью управления процессами. Подстроечные используются для корректировки режимов при наладке и после ремонта;
- материал рабочей части резистора. Металлы, их окислы и сплавы, графитовые или композитные смеси;
- вид резистивных тел. Проволока, фольга или ленты из метала, напыление пленки на керамику, интегрированные каналы в микросхеме;
- способ размещения. Резисторы могут быть впаяны в электронную плату, устанавливаться отдельно на панели управления или закладываться при создании микросхемы внутри изделия;
- характер изменения падения напряжения на элементе от внешних условий (ВАХ). Вольт-амперная характеристика в рабочем диапазоне резистора может быть линейной или нелинейной.
Нелинейная ВАХ отражает изменение сопротивления компонента от внешних условий. Такие резисторы служат датчиками напряжения (варисторы), магнитного поля (магниторезисторы), уровня освещенности (фоторезисторы), перепада температуры (терморезисторы), изменения деформации (тензорезисторы).
Сопротивление резистора
У тех, кто только начинает изучать азы электротехники, часто возникает вопрос, а чем отличается резистор от сопротивления. Разница в том, что резистор является пассивным элементом электроцепи, а сопротивление — это характеристика данного элемента, которую можно рассчитать, определить по маркировке или измерить. Но зачастую сопротивление используется в качестве синонима слова «резистор».
Рассчитать внутреннее сопротивление резистора в сети постоянного тока помогает формула закона Ома для элемента цепи:
Эту формулу применяют также для расчета активного сопротивления в сети переменного тока, но используют действующий ток через элемент. Он равен постоянному току, при котором выделяется на резисторе столько же теплоты, сколько за одинаковое время при прохождении импульсного или синусоидального тока различной частоты.
Суммарное электрическое сопротивление в сетях переменного тока вычисляется при учете активной и реактивной составляющей участка цепи. Любой вид сопротивления измеряется в омах.
Одинокий резистор в схеме часто используется как ограничитель тока. На электронных платах этих элементов много. Друг с другом они соединяются в различных комбинациях: последовательно, параллельно или по смешанной системе.
Последовательная цепь источника и сопротивлений
В замкнутом контуре из последовательно соединенных резисторов и батареи ток в разных точках цепи имеет одинаковое значение. Показание вольтметра на отдельном резисторе будет отражать произведение его внутреннего сопротивления на ток в контуре. Суммарные показания вольтметров будут равны напряжению источника, а для определения общего сопротивления резисторов надо сложить сопротивления всех элементов.
Последовательную цепочку сопротивлений часто используют как делитель напряжения в маломощных измерительных или задающих ступенчатое управление параметрами устройствах. Сопротивление нагрузки Rн, подключенной параллельно R1 вместо вольтметра, должно быть немного больше, чтобы делитель работал стабильно.
Параллельная схема элементов
При параллельном соединении на каждом элементе присутствует напряжение источника, общий ток равен сумме токов резисторов. Расчет сопротивления участка цепи осуществляется по формуле R = (R1 • R2) / (R1 + R2).
Отличие параллельного соединения от последовательного заключается в том, что каждый резистор получает напряжение, которое равно напряжению источника, а общее сопротивление участка меньше меньшего из его составляющих.
Расчет смешанного соединения элементов схемы
Перед тем как рассчитать общее сопротивление схемы, состоящей из параллельных и последовательных участков, используют методы упрощения. На каждом шаге упрощенные эквивалентные схемы можно посчитать по уже известным формулам. Полученный в результате резистор будет обладать общим сопротивлением исходной схемы.
Мощность рассеивания
Для надежной работы электрической схемы нужно знать и сопротивление резистора, и мощность рассеивания, формула для вычисления последней имеет вид:
Правильно подобранный элемент схемы должен рассеять мощность Р (Вт) не разрушаясь и не нагревая другие детали.
Параметры резисторов
Выбор резисторов происходит чаще всего по следующим основным параметрам:
- номинальному сопротивлению. Подбирается или подгоняется ближайшее к расчетному;
- допуску — характеристика, отражающая точность при изготовлении номинального сопротивления. Она составляет 5–20%;
- номинальной мощности рассеивания. Наибольшая величина рассеянного тепла без изменения характеристик меньше номинала элемента;
- предельному рабочему напряжению. Приложенное к выводам резистора наибольшее напряжение, которое не разрушает его;
- температурный коэффициент. Показывает, как изменится сопротивление резистора при колебании на один градус температуры среды.
Для переменных резисторов учитывают ряд дополнительных характеристик:
- износоустойчивость — число циклов;
- функцию изменения сопротивления (линейная, логарифмическая, обратнологарифмическая);
- уровень шума при движении ползунка.
Определение параметров по маркировке и схеме
Некоторые из параметров наносятся непосредственно на резисторы, например, сопротивление и допуск. Раньше для информации о них использовали буквы и цифры. Номинальное сопротивление резисторов имеет диапазон от 0.01 Ом до 1 ГОм. Цифры в маркировке обозначают номинал, а буквы — множитель. Конкретная величина получается умножением или делением цифр.
Буквенно-цифровая маркировка предполагает использование букв Е и R для сопротивлений до 99 Ом, выше — К, а уровень мегаомов обозначается буквой М. В зависимости от того, какую позицию занимает буква в цифровом коде, определяются целые числа или дробные. Узнать, какому множителю соответствует определенная буква, поможет специальная таблица, которую можно найти в любом справочном пособии.
Элементы с цифро-буквенной маркировкой сейчас можно найти преимущественно в старой аппаратуре. В ходе ее ремонта часто приходится менять резисторы, поэтому необходимо уметь расшифровывать такое обозначение.
Сейчас в угоду минимизации отказались от буквенно-цифровых обозначений. На поверхность резисторов наносится маркировка кольцами или точками разных цветов. Чтобы определить по полоскам сопротивление резистора, следует начинать со смещенной к одному из выводов или самой широкой цветной полоски.
Набор цветов первых трех колец при 5 и 6-полосной раскраске означает шифр сопротивления резистора, цвет четвертого кольца обозначает определенное значение множителя для него. Цвет пятого кольца показывает точность изготовления резистора. При шестиполосной окраске цвет последнего кольца обозначает изменение сопротивления (процент) при перепаде температуры окружающей среды на 1 градус. Четырех и пятиполосная раскраска его не имеет.
При четырехполосной маркировке сопротивление резисторов определяется по цветам первых двух. Цвет третьей полосы — это множитель для точного определения сопротивления. Последняя полоса своей расцветкой говорит о допуске в процентах от номинала.
На электрической схеме резистор изображается в виде прямоугольника с размерами 4×10 мм. Рядом с изображением указывается буква R и цифра, обозначающая порядковый номер элемента на схеме, например, R1. Указывается также номинальное сопротивление. Как определить его по буквенно-цифровой маркировке, было рассказано выше.
Мощность рассеивания указывается на графическом изображении специальными метками, если этот параметр меньше 1 ватта. Как узнать мощность по ним подскажет таблица, приведенная ниже.
Если мощность рассеивания выше одного ватта, то внутри прямоугольника ставят римскую цифру. Например, V используется для мощности величиной 5 Вт, Х — 10 Вт и т. п.
Бывают случаи, когда нет возможности воспользоваться маркировкой, например, если она повреждена или стерта. В таком случае нужно знать, как измерить сопротивление специальным прибором. Это может быть омметр или мультиметр. Они мало чем отличаются, но последний является многофункциональным прибором. Принцип измерений основывается на законе Ома. Перед тем как проверить резистор, следует выставить рабочий режим и диапазон измеряемого сопротивления.
Алгоритм по измерению сопротивления используется такой:
Резистор является довольно простым элементом и по своему устройству, и по принципу работы. Поэтому его сопротивление определяется также довольно просто. Еще больше облегчают задачу онлайн-калькуляторы. Ими можно воспользоваться, если возникает необходимость рассчитывать сопротивление многих элементов, для соединения которых применяются разные способы, а также для расшифровки маркировки в виде цветных полос.
Видео по теме
Закон Ома
- Главная
- /
- Физика
- /
- Закон Ома
Чтобы посчитать Закон Ома воспользуйтесь нашим очень удобным онлайн калькулятором:
Закон Ома для участка цепи
Закон Ома для участка цепи гласит, что сила тока (I) на участке электрической цепи прямо пропорциональна напряжению (U) на концах участка цепи и обратно пропорциональна его сопротивлению (R).
Онлайн калькулятор
Найти силу тока
Напряжение: U =В
Сопротивление: R =Ом
Сила тока: I =
0
А
Формула
I = U/R
Пример
Если напряжение на концах участка цепи U = 12 В, а его электрическое сопротивление R = 2 Ом, то:
Сила тока на этом участке I = 12/2= 6 А
Найти напряжение
Сила тока: I =A
Сопротивление: R =Ом
Напряжение: U =
0
В
Формула
U = I ⋅ R
Пример
Если сила тока на участке цепи I = 6 А, а электрическое сопротивление этого участка R = 2 Ом, то:
Напряжение на этом участке U = 6⋅2 = 12 В
Найти сопротивление
Напряжение: U =В
Сила тока: I =A
Сопротивление: R =
0
Ом
Формула
R = U/I
Пример
Если напряжение на концах участка цепи U = 12 В, а сила тока на участке цепи I = 6 А, то:
Электрическое сопротивление на этом участке R = 12/6 = 2 Ом
Закон Ома для полной цепи
Закон Ома для полной цепи гласит, что сила тока в цепи пропорциональна действующей в цепи электродвижущей силе (ЭДС) и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника.
Онлайн калькулятор
Найти силу тока
ЭДС: ε =В
Сопротивление всех внешних элементов цепи: R =Ом
Внутреннее сопротивление источника напряжения: r =Ом
Сила тока: I =
0
А
Формула
I = ε/R+r
Пример
Если ЭДС источника напряжения ε = 12 В, сопротивление всех внешних элементов цепи R = 4 Ом, а внутреннее сопротивление источника напряжения r = 2 Ом, то:
Сила тока I = 12/4+2 = 2 А
Найти ЭДС
Сила тока: I =А
Сопротивление всех внешних элементов цепи: R =Ом
Внутреннее сопротивление источника напряжения: r =Ом
ЭДС: ε =
0
В
Формула
ε = I ⋅ (R+r)
Пример
Если сила тока в цепи I = 2A, сопротивление всех внешних элементов цепи R = 4 Ом, а внутреннее сопротивление источника напряжения r = 2 Ом, то:
ЭДС ε = 2 ⋅ (4+2) = 12 В
Найти внутреннее сопротивление источника напряжения
Сила тока: I =А
ЭДС: ε =В
Сопротивление всех внешних элементов цепи: R =Ом
Внутреннее сопротивление источника напряжения: r =
0
Ом
Формула
r = ε/I – R
Пример
Если сила тока в цепи I = 2A, сопротивление всех внешних элементов цепи R = 4 Ом, а ЭДС источника напряжения ε = 12 В, то:
Внутреннее сопротивление источника напряжения r = 12/2 – 4 = 2 Ом
Найти сопротивление всех внешних элементов цепи
Сила тока: I =А
ЭДС: ε =В
Внутреннее сопротивление источника напряжения: r =Ом
Сопротивление всех внешних элементов цепи: R =
0
Ом
Формула
R = ε/I – r
Пример
Если сила тока в цепи I = 2A, внутреннее сопротивление источника напряжения r = 2 Ом, а ЭДС источника напряжения ε = 12 В, то:
Сопротивление всех внешних элементов цепи: R = 12/2 – 2 = 4 Ом
См. также
Онлайн калькулятор закона Ома позволяет определять связь между силой тока, электрическим напряжением и сопротивлением проводника в электрических цепях.
Для расчета, вам понадобится воспользоваться отдельными графами:
– сила тока вычисляется в Ампер, исходя из данных напряжения (Вольт) и сопротивления (Ом);
– напряжение вычисляется в Вольт, исходя из данных силы тока (Ампер) и электрического сопротивления (Ом);
– электрическое сопротивление вычисляется в Ом, исходя из данных силы тока (Ампер) и напряжения (Вольт);
– мощность вычисляется в Ватт, исходя из данных силы тока (Ампер) и напряжения (Вольт).
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Смотрите также
Закон Ома
Закон Ома — главный закон электротехники, который открыл в 1826 году выдающийся немецкий ученый Георг Симон Ом. Вместе с экспертом разберем формулировку, формулу и задачи на закон Ома с решением
Физика — наука эмпирическая. Ее основные законы вытекают из практического опыта и частенько много лет не имеют теоретических обоснований. Именно так обстоит дело с главным законом электротехники, который открыл в 1826 году выдающийся немецкий ученый Георг Симон Ом.
Электрические явления люди наблюдали сотни лет. Но никак не связывали между собой заряженность потертого янтаря и молнию. Только на исходе XVIII столетия электричество стали внимательно исследовать. В 1795 году Алессандро Вольта изобрел «вольтов столб», химическую батарею, и обнаружил появление тока в проводнике, соединяющем ее полюса. Сферы применения электричества стремительно множились, и появилась острая необходимость в расчетных формулах для инженеров. Эту задачу решали многие ученые, но первым сформулировал главную формулу электротехники именно Георг Ом. Он ввел в обиход понятие сопротивления и опытным путем установил зависимость между основными характеристиками электрической цепи.
Определение закона Ома простыми словами
Электрическая цепь состоит из двухполюсного источника напряжения, то есть батареи, аккумулятора или генератора. Если полюса источника соединить проводами, то по ним потечет электрический ток. Его величина определяется сопротивлением проводников. Наглядное представление этой зависимости — обыкновенный водопровод. Аналогом источника напряжения является насос или водонапорная башня, создающая давление в магистрали, количество воды, прошедшее по трубе, — подобие силы тока, а кран соответствует сопротивлению. Полностью открытый, он не ограничивает поток, по мере закручивания отверстие для воды уменьшается, пока не закроется совсем.
Закон Ома для участка цепи
Опытным путем исследователь установил взаимосвязь характеристик электрической цепи. Классическая формулировка закона Ома звучит так:
«Сила тока на участке цепи прямо пропорциональна напряжению и обратно пропорциональна сопротивлению».
Формула закона Ома для участка цепи
В таком виде закон Ома приведен в школьных учебниках физики. Согласно этой простой формуле, для определения уровня тока в проводнике достаточно величину напряжения на его сторонах разделить на некий условно постоянный коэффициент, то есть на сопротивление. Почему «условно»? Потому что величина сопротивления может меняться в зависимости от температуры. Поэтому, кстати, лампы накаливания чаще всего перегорают при включении. Сопротивление холодной спирали ниже, чем нагретой, скачок тока при подаче напряжения вызывает ее резкое расширение и разрыв. Но если этот момент преодолен и нить накала уцелела, то ее сопротивление растет, и ток ограничивается. А при температуре жидкого гелия, например, сопротивление падает до нуля, наступает сверхпроводимость.
Закон Ома для замкнутой полной цепи
Предыдущая формулировка годится только для участка цепи, где отсутствует сам источник электродвижущей силы. В реальности ток течет по замкнутому контуру, где обязательно есть батарея или генератор, имеющий собственное внутреннее сопротивление. Поэтому формула закона Ома для полной цепи выглядит несколько сложнее
Формула закона Ома для замкнутой полной цепи
Применение закона Ома
Георг Ом дал в руки инженеров средство для решения задач, связанных с электрическими цепями. Тепловые и световые приборы, электродвигатели, генераторы, линии электропередач, кабели связи рассчитываются на основе этой простой формулы. Нет такой области электротехники, где она не находит применения. Даже в радиотехнике используется закон Ома, но в дифференциальной форме. «Все гениальное — просто», как считали Еврипид, Леонардо да Винчи, Наполеон Бонапарт и Альберт Эйнштейн, несомненные гении. Закон Ома целиком и полностью подтверждает эту истину.
Сила трения
Единицы измерения силы трения, от чего она зависит и какие виды существуют
подробнее
Задача на закон Ома с решением
Задача для участка электрической цепи
Электрочайник, включенный в сеть с напряжением 220 В, потребляет ток 1,1 А. Каково сопротивление электрочайника.
Дано:
U = 220 В
I = 1,1 А
Решение:
Согласно закону Ома для участка цепи:
R=U/I=220/1,1=200 Ом
Ответ: R = 200 Ом.
Задача для полной замкнутой цепи
Источник постоянного тока с ЭДС E = 24 В и внутренним сопротивлением r = 1,5 Ом замкнут на внешнее сопротивление R = 11 Ом. Определить силу тока в цепи.
Дано:
Е=24 В, r=1,5 Ом, R = 11 Ом
Решение:
По закону Ома для замкнутой цепи: I = E/(R + r) = 24/(11+1,5) = 1,92 А.
Ответ: I=1, 92 А.
Популярные вопросы и ответы
Отвечает Николай Герасимов, старший преподаватель физики в Домашней школе «ИнтернетУрок».
Сколько всего законов Ома в физике?
Существует два закона Ома: закон Ома для участка цепи и закон Ома для полной (замкнутой) цепи. Первый связывает сопротивление участка, силу тока в нём и разность потенциалов (напряжение) на его концах. Кроме того, в нем отражено наличие в цепи источника тока.
Второй учитывает и потребителей электрического тока (электрические лампы, обогреватели, телевизоры и так далее), и его источники (генераторы, батарейки, аккумуляторы). Дело в том, что любой источник тока обладает внутренним сопротивление, которое влияет на силу тока. Именно это и учитывается в законе Ома для полной (замкнутой) цепи.
При каких условиях выполняется закон Ома?
Согласно закону Ома, существует линейная зависимость между силой тока в участке цепи и напряжением на его концах. Он отлично выполняется для металлических проводников при любых напряжениях, а вот для тока в вакууме, газе, растворах или расплавах электролитов, полупроводниках линейная зависимость нарушается, и применять закон Ома в том виде, в котором его изучают в школьном курсе, уже нельзя.
Для чего нужен закон Ома?
Трудно переоценить значимость этого закона. Он позволил производить расчет электрических цепей, без которых практически невозможно представить жизнь современного человека, так как они лежат в основе любого электроприбора, начиная от обычной лампы накаливания и заканчивая самыми современными компьютерами.
В каком классе проходят закон Ома?
В школьном курсе ученики впервые знакомятся с электрическими явлениями и законом Ома для участка цепи в 8 классе. Более подробно о причинах возникновения электрического тока и его источниках ученики знакомятся в курсе старшей школы (10 или 11 класс, в зависимости от программы). Здесь же ученики впервые встречаются и с законом Ома для полной (замкнутой) цепи.