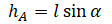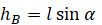Айгулик
Ученик
(120),
закрыт
10 лет назад
Лучший ответ
дэв
Просветленный
(28590)
10 лет назад
ты совсем тупая или как? высота тебе известна, сила притяжения земли тоже, остаётся только взвесить падающий предмет
Остальные ответы
Валентина Вавилова(Серкова)
Гений
(62183)
10 лет назад
По закону сохранения энергии: потенциальная энергия в верхней точке = кинетической энергии в точке падения.
Еп=Ек.
Еп=m*g*h .
Ек=m*v^2 / 2. приравняем.
m*g*h = m*v^2 / 2. сократим на массу.
g*h = v^2 / 2. выразим скорость
v=корень квадратный из 2*g*h.
v=кор. кв. из 2*10*20=20м/c.
Похожие вопросы
Закон сохранения энергии
Энергия — одно из сложнейших понятий современной физики. И закон сохранения энергии относится к числу ее основополагающих принципов. Вместе с экспертом разберем задачи с решением этого фундаментального закона природы и узнаем, кто его открыл
Физика ставит своей целью понимание самых общих закономерностей материального мира. Имена Архимеда, Ньютона, Эйнштейна знакомы каждому школьнику. Но великое множество ученых вложили по кирпичику в здание современной науки и ускорили развитие человеческой цивилизации. Ее современный уровень был бы недостижим без понимания природы энергии и ее законов прежде всего в механике, самом доступном для наблюдений и экспериментов разделе физики.
Формулировка закона сохранения энергии простыми словами в механике
Закон сохранения энергии действует повсеместно и незаметно. В механике он срабатывает в замкнутой системе под воздействием консервативных сил – то есть сил тяжести и упругости, зависящих только от стартового и финального положения тела и не зависящих от траектории движения. При таких условиях энергия тел никуда не исчезает, а лишь переходит из кинетической в потенциальную и наоборот – из потенциальной в кинетическую. Это и есть самая простая формулировка закона сохранения энергии для механических систем.
Формула закона сохранения энергии
E=Ep+Ek=const
Где:
Ep — потенциальная энергия;
Ek — кинетическая энергия;
История открытия закона сохранения энергии
Закономерности взаимодействия физических тел интересовали ученых с античных времен. Но описать их в виде формулы или хотя бы принципа они не сумели. Первым это попытался сделать Рене Декарт в своем труде «Начала философии», изданном в середине XVII века. Он указал, что если одно тело сталкивается с другим, то может отдать ему только такое количество движения, сколько второе у него отнимет. Идею Декарта развил Лейбниц, введя понятие «живой силы», которую мы называем кинетической энергией. Поддержал его рассуждения Михайло Ломоносов в своем «всеобщем естественном законе», но все формулировки были скорее принципом, а не законом, формул не было.
От «живой силы» физики перешли к «кинетической энергии» только в середине XIX столетия, накопив опыт работы с тепловыми и электрическими машинами. Немалый экспериментальный вклад сделал в понимание этого закона Джеймс Джоуль и Роберт Майер. Самую полную математическую формулировку дал Герман Гельмгольц, который ввел понятие потенциальной энергии и обобщил закон сохранения энергии на все разделы физики – даже на те, которые в его время не существовали. Например, на теорию относительности и квантовую механику.
Задачи на закон сохранения энергии
Самый общий физический закон используется при решении совершенно практических задач.
Задача 1
Некое тело подбросили вверх вертикально с начальной скоростью 15 м/с. На какую высоту оно поднимется? Сопротивление воздуха при решении задачи не учитывать.
Решение: полученная при броске кинетическая энергия будет постепенно преобразовываться в потенциальную энергию:
Ep=Ek
То есть: mgh=(m*V2)/2
Где:
m – масса тела;
V – начальная скорость;
g – ускорение свободного падения;
h – высота подъема.
После преобразований получаем формулу для высоты подъема:
h= V2/(2*g)=225/(2*9,8)=11,47 м.
Ответ: тело поднимется на высоту 11,47 м.
Сила Архимеда
Формула и определение силы Архимеда простыми словами
подробнее
Задача 2
Пружину растянули на 15 см. Известно, что она получила потенциальную энергию 24 Дж. Какова жесткость пружины?
Решение: формула потенциальной энергии упруго деформированного тела:
Ep=(k*x2)/2
Где:
k – коэффициент жесткости;
x – величина деформации.
Преобразуем формулу для расчета:
k=(2*Ep)/x2=(2*24)/225=2133,33 Н/м
Ответ: жесткость пружины равна 2133,33 Н/м.
Популярные вопросы и ответы
Отвечает Андрей Найденов, преподаватель математики и физики онлайн-школы TutorOnline.
Кто открыл закон сохранения энергии?
В открытии закона сохранения энергии участвовали многие ученые. Некоторые из них были очень близки, чтобы сформулировать его. Например, Майер и Джоуль своими работами показали, что количество выделяемой теплоты равно совершенной работе и наоборот. Однако наиболее полную формулировку первым дал в своих работах Гельмгольц.
Какие примеры из жизни на закон сохранения энергии существуют?
Таких примеров множество. Пример с молотком и гвоздем хорошо иллюстрирует переход механической энергии от молотка к гвоздю. Закон сохранения энергии здесь в том, что сколько молоток при ударе энергии отдал, столько же энергии гвоздь и получил. Ни больше ни меньше.
Другой пример. Кубики льда, взятые при температуре 0º С и опущенные в бокал с газированной водой, растаят, если им сообщить столько же Джоулей тепла, сколько забрали тепла у воды, взятой при температуре 0º С, когда ее замораживали, чтобы она перешла в твердое агрегатное состояние – лед. А если газированная вода будет недостаточно теплой, то лед не растает. Однако если этот бокал оставить на столе надолго, лед все равно растает, так как он получит необходимое количество тепла из окружающего воздуха.
Еще пример. Когда болит горло, есть хороший бабушкин рецепт. Надо пить теплое молоко. Молоко прогревает горло, отдает тепло, что помогает лечению. Молоко при этом остывает в горле и не греет желудок, что тоже важно.
Во всех этих примерах можно наблюдать большие потери тепла на нагрев окружающих тел. Но основная часть энергии идет на полезное действие. Сколько энергии отдает одно тело, столько же получает и другое, минус потери тепла на нагрев окружающих тел.
Если исключить потери тепла, можно добиться очень высокой эффективности процесса. Это возможно в системах, где энергия не выходит наружу и не рассеивается, поэтому ее потери минимальные. Примером такой системы может служить термос. Горячая вода в термосе долго не остывает, потому что потери тепла минимальные.
Когда сохраняется полная механическая энергия?
Полная механическая энергия сохраняется в системах, которые называются изолированными. Получить полностью изолированную систему достаточно сложно. Всегда найдутся силы, которые будут действовать на тело или систему из нескольких тел извне.
Хорошим примером может стать жизнь космонавтов на орбитальном комплексе, вращающемся вокруг Земли. Если космонавт оттолкнется от пола на Земле, то сила притяжения быстро вернет его обратно на пол.
В орбитальном комплексе сила притяжения к Земле скомпенсирована движением корабля по круговой орбите. Состояние невесомости позволяет космонавту оттолкнутся от пола и лететь вверх неопределенно долго, пока он не столкнется с потолком. Тело космонавта можно считать изолированной системой, так как на него не действуют силы извне, а силы сопротивления движению со стороны воздуха в корабле минимальны.
В каком классе изучают закон сохранения энергии?
Здесь есть одна тонкость. Закон сохранения механической энергии изучают на уроках физики в седьмом классе. А закон сохранения энергии, применительно к тепловым процессам, с использованием понятия внутренней энергии тела, изучают уже в восьмом классе.
В механике все силы делятся на две группы: консервативные и неконсервативные.
Консервативные силы
Консервативными, или потенциальными, называются такие силы, работа которых не зависит от траектории, а определяется только начальным и конечным положениями тела. Работа таких сил по перемещению тела по замкнутой траектории всегда равна нулю. Примеры потенциальных (консервативных) сил:
- сила тяжести
- сила упругости
- гравитационная сила
Неконсервативные силы
Неконсервативными называются такие силы, работа которых зависит от траектории. Сама сила в этом случае зависит от модуля и направления вектора скорости. Работа таких сил может приводить к выделению тепла — часть механической энергии при этом превращается в тепловую. Примеры неконсервативных сил:
- сила упругости
- сила сопротивления среды
Полная механическая энергия — это сумма потенциальной и кинетической энергии тела в определенный момент времени:
E = Ek + Ep
Закон сохранения механической энергии
В замкнутой системе, в которой действуют консервативные силы, механическая энергия сохраняется.
E = const
Определение
Замкнутая система — это система, в которой тела, входящие в нее, взаимодействуют только друг с другом, а влиянием внешних сил можно пренебречь.
Согласно закону сохранения энергии, сумма потенциальной и кинетической энергии системы до взаимодействия тел равна сумме потенциальной и кинетической энергий системы после их взаимодействия:
Ek0 + Ep0 = Ek + Ep
Закон сохранения механической энергии для движения в поле тяжести Земли
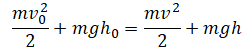
Примеры определения полной механической энергии в начальном и конечном положении
| Пример | Полная механическая энергия в начальной точке (А) | Полная механическая энергия в конечной точке (В) |
|
Спуск по наклонной плоскости из состояния покоя
|
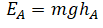
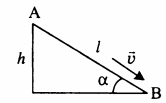
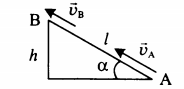
Высоту, на которой изначально находилось тело, можно рассчитать по формуле:
|
 |
|
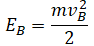Подъем по наклонной плоскости
|
 |
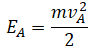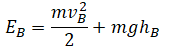
Высоту, на которую поднялось тело, можно рассчитать по формуле:
|
|
Груз на нити
|
Высоту, на которой изначально находилось тело, можно рассчитать по формуле:
|
 |
|
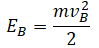Вертикальный выстрел из пружинного пистолета |
 |
 |
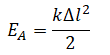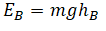Пример №1. Камень брошен вертикально вверх. В момент броска он имел кинетическую энергию, равную 30 Дж. Какую потенциальную энергию относительно поверхности земли будет иметь камень в верхней точке траектории полета? Сопротивлением воздуха пренебречь.
Так как это условно замкнутая система (сопротивлением воздуха мы пренебрегаем), мы можем применить закон сохранения энергии:
Ek0 + Ep0 = Ek + Ep
Учтем, что в момент броска камень находился на поверхности земли. Поэтому он обладал максимальной кинетической энергией и нулевой потенциальной. Но в верхней точке траектории его скорость стала равна нулю. Поэтому его кинетическая энергия тоже стала равна нулю. Зато потенциальная энергия в этой точке возросла до максимума. Поэтому:
Ek0 + 0 = 0 + Ep
Ek0 = Ep
Следовательно, потенциальная энергия в верхней точки траектории полета равна 30 Дж.
Задание EF19083
Шарик массой 100 г падает с высоты 100 м с начальной скоростью, равной нулю. Чему равна его кинетическая энергия в момент перед падением на землю, если потеря энергии за счёт сопротивления воздуха составила 20 Дж?
Алгоритм решения
- Записать исходные данные и перевести единицы измерения величин в СИ.
- Записать закон сохранения механической энергии.
- Записать закон сохранения применительно к задаче.
- Выполнить общее решение.
- Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
- Масса шарика: m = 100 г.
- Высота, с которой начал падать шарик: h = 100 м.
- Энергия, потерянная за счет сопротивления воздуха: Q = 20 Дж.
100 г = 0,1 кг
Закон сохранения механической энергии для замкнутой системы:
Ek0 + Ep0 = Ek + Ep = const
Согласно условию задачи, система не является замкнутой, так как на шарик действует сила сопротивления воздуха. Поэтому закон сохранения энергии примет вид:
Ek0 + Ep0 = Ek + Ep + Q
Шарик начал падать из состояния покоя, поэтому начальная кинетическая энергия равна нулю. В момент приземления кинетическая энергия максимальная, а потенциальная равна нулю. Поэтому:
Ep0 = Ek + Q
Потенциальная энергия определяется формулой:
Ep0 = mgh
Следовательно:
mgh = Ek + Q
Отсюда кинетическая энергия шарика в момент перед падением на землю равна:
Ek = mgh – Q = 0,1∙10∙100 – 20 = 80 (Дж)
Ответ: 80
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17731
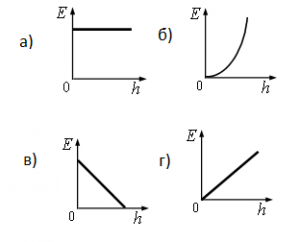Какой из графиков, приведённых на рисунке, показывает зависимость полной энергии Е тела, брошенного под углом к горизонту, от его высоты h над Землёй? Сопротивлением воздуха пренебречь.
Алгоритм решения
- Записать закон сохранения энергии.
- Установить зависимость полной механической энергии от высоты.
- Найти тип графику, соответствующий выявленной зависимости.
Решение
Запишем закон сохранения механической энергии:
E = const
Полная механическая энергия тела равна:
E = Ek + Ep
Исходя из закона, сумма потенциальной и кинетической энергии в начальный момент движения тела равно сумме потенциальной и кинетической энергии в конечный момент времени:
Ek0 + Ep0 = Ek + Ep
Так как полная механическая энергия не меняется с течением времени, ее графиком должна быть прямая, параллельная оси времени. Поэтому верный ответ — а.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22589
Тело, брошенное вертикально вверх от поверхности Земли, достигло максимальной высоты 20 м. С какой начальной скоростью тело было брошено вверх? Сопротивлением воздуха пренебречь.
Ответ:
а) 4,5 м/с
б) 10 м/с
в) 20 м/с
г) 40 м/с
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Записать закон сохранения механической энергии.
3.Записать закон сохранения применительно к задаче.
4.Выполнить общее решение.
5.Подставить известные данные и вычислить искомую величину.
Решение
Из условия задачи известна только высота h = 20 м.
Закон сохранения механической энергии для замкнутой системы:
Ek0 + Ep0 = Ek + Ep = const
Тело изначально находилось на поверхности Земли, поэтому его начальная потенциальная энергия равна нулю. Но кинетическая энергия в момент броска была максимальной. В верхней точке траектории скорость тела нулевая, поэтому кинетическая тоже равна нулю. Но потенциальная энергия в этот момент времени максимальна.
Поэтому:
Ek0 = Ep
Кинетическая и потенциальная энергии определяются формулами:
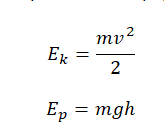
Приравняем их:
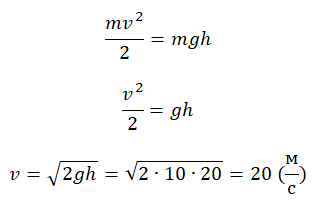
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17696
Если многократно сжимать пружину, то она нагревается. Это можно объяснить тем, что
Ответ:
а) потенциальная энергия пружины переходит в кинетическую
б) кинетическая энергия пружины переходит в потенциальную
в) часть работы внешних сил переходит во внутреннюю энергию пружины
г) пружина нагревается в процессе ударов молекул воздуха о частицы вещества пружины
Алгоритм решения
- Сформулировать закон сохранения механической энергии.
- Установить причины нагревания пружины.
Решение
Закон сохранения механической энергии формулируется так: «Полная механическая энергия замкнутой системы постоянна».
Замкнутая система — эта система, составные элементы которой действуют только друг с другом, и внешние силы на систему не действуют. Но если пружину сжимать и разжимать много раз, то пружина не будет являться замкнутой системой. Поэтому закон сохранения энергии в ней не сохраняется. Но ни потенциальная, ни кинетическая энергии, ни их превращение друг в друга не вызывает нагревания. К этому может привести только воздействие внешней силы, часть которой переходит во внутреннюю.
Верный ответ – в.
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18127
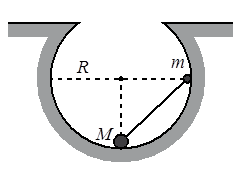Небольшие шарики, массы которых m = 30 г и M = 60 г, соединены лёгким стержнем и помещены в гладкую сферическую выемку.
В начальный момент шарики удерживаются в положении, изображённом на рисунке. Когда их отпустили без толчка, шарики стали скользить по поверхности выемки. Максимальная высота подъёма шарика массой М относительно нижней точки выемки оказалась равной 12 см. Каков радиус выемки R?
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Сделать чертеж конечного положения шариков. Обозначить их высоты, выбрать нулевой уровень отсчета потенциальной энергии. Выбрать систему координат.
3.Записать закон сохранения энергии.
4.Выполнить общее решение задачи.
5.Подставить известные данные и выполнить вычисление искомой величины.
Решение
Запишем исходные величины:
• Масса первого шарика: m = 30 г.
• Масса второго шарика: M = 60 г.
• Максимальная высота подъема шарика М: H = 12 см.
Переведем единицы измерения величин в СИ:
30 г = 0,03 кг
60 г = 0,06 кг
12 см = 0,12 м
Выполним чертеж:
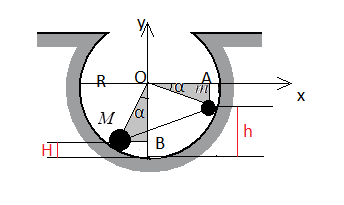
Нулевой уровень — нижняя точка выемки.
Запишем закон сохранения энергии:
Ek0 + Ep0 = Ek + Ep = const
В начальном положении кинетическая энергия обоих шариков равна 0. Потенциальная энергия шарика М тоже равна нулю, так как он находится на нулевом уровне. Потенциальная энергия шарика m равна:
Ep0m = mgR
Кинетическая энергия шариков после установления равновесия тоже будет равна нулю. Но b[ потенциальная энергия будет отличной от нуля:
Epm = mgh
EpM = MgH
Поэтому закон сохранения энергии применительно к задаче примет вид:
mgR = mgh + MgH
Преобразуем выражение и получим:
mgR−mgh=MgH
R−h=MgHmg=MHm
При движении гантели по поверхности выемки высоты подъема большого и малого шаров связаны. Рассмотрим прямоугольные треугольники OmA и OMB. Для них справедливы следующие равенства:
MB = mA = R – h
OA = OB = R – H
OM = Om = R
Это дает нам право воспользоваться теоремой Пифагора:
(R−h)2=R2−OA2=R2−(R−H)2
Следовательно:
(R−h)2=R2−(R2−2RH+H2)=2RH−H2
Подставим в это выражение правую часть ранее полученного выражения:
R−h=MHm
(MHm)2=2RH−H2
Теперь можем выразить и вычислить радиус:
2RH=(MHm)2+H2
R=(MHm)2+H22H
R=(Mm)2H2+H2=(0,060,03)20,122+0,122=0,3 (м)
Ответ: 0,3
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18087
Шайба массой m, скользящая по гладкой горизонтальной поверхности, налетает на лежащую неподвижно на той же поверхности шайбу массой 3m такого же размера. После частично неупругого удара первая шайба остановилась. Какова была кинетическая энергия первой шайбы до удара, если при ударе выделилось количество теплоты Q?
Ответ:
а) 3Q/2
б) 2Q
в) 9Q/2
г) 8Q
Алгоритм решения
1.Записать исходные данные.
2.Записать закон сохранения импульса.
3.Записать закон сохранения энергии с учетом выделения тепла при ударе.
4.Выполнить решение в общем виде.
5.Выразить искомую величину.
Решение
Запишем исходные данные:
• Масса второй шайбы: 3m.
• Количество выделенной теплоты при ударе: Q.
До удара двигалась только первая шайба, вторая покоилась, поэтому импульс второй шайбы равен нулю. После удара первая шайба остановилась, поэтому ее импульс стал равен нулю. Но начала двигаться вторая шайба. Поэтому закон сохранения импульса при ударе примет вид:
mv=3mV
Отсюда скорость второй шайбы равна v/3.
Запишем закон сохранения энергии с учетом того, что при ударе выделилось тепло:
Ek1=Ek2+Q
Кинетическую энергию второй шайбы можно выразить как доля от кинетической энергии первой шайбы, а также как произведение половинной массы на половинный квадрат:
Ek2=Ek1x=3mV22=3mv22·9
x — доля кинетической энергии второй шайбы от кинетической энергии первой шайбы.
Кинетическая энергия первой шайбы равна:
Ek1=mv22
Теперь можем выразить x:
3mv22·9=mv22x
x=13
Следовательно, на кинетическую энергию второй шайбы ушла 1/3 часть кинетической энергии первой шайбы, а в виде тепла выделилось 2/3 этой энергии. Отсюда:
Q=23Ek1
Ek1=32Q
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18122
Летящая горизонтально со скоростью 20 м/с пластилиновая пуля массой 9 г попадает в груз неподвижно висящий на нити длиной 40 см, в результате чего груз с прилипшей к нему пулей начинает совершать колебания. Максимальный угол отклонения нити от вертикали при этом равен α = 60°. Какова масса груза?
Ответ:
а) 27 г
б) 64 г
в) 81 г
г) 100 г
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Сделать чертеж, отобразив начальное, промежуточное и конечное положение тел.
3.Записать закон сохранения импульса для момента столкновения и закон сохранения механической энергии для момента максимального отклонения нити от положения равновесия.
4.Выполнить решение задачи в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса пластилиновой пули: m = 9 г.
• Скорость пластилиновой пули: v = 20 м/с.
• Максимальный угол отклонения нити: α = 60°.
Переведем единицы измерения величин в СИ:
Сделаем чертеж:
Нулевой уровень — точка А.
После неупругого столкновения пули с грузом они начинают двигаться вместе. Поэтому закон сохранения импульса для точки А выглядит так:
mv=(m+M)V
После столкновения система тел начинается двигаться по окружности. Точка В соответствует верхней точке траектории. В этот момент скорость системы на мгновение принимает нулевое значение, а потенциальная энергия — максимальное.
Закон сохранения энергии для точки В:
(m+M)V22=(m+M)gh
V22=gh
Высоту h можно определить как произведение длины нити на косинус угла максимального отклонения. Поэтому:
V=√2glcosα
Подставим это выражение в закон сохранения импульса для точки А и получим:
Выразим массу груза:
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 6.6k
Статьи
Линия УМК А.В. Перышкина. Физика (7-9)
Физика
Закон сохранения механической энергии
Удивительно, но закон сохранения механической энергии — базовый закон механики — открыл немецкий корабельный доктор Роберт Юлий Майер, а не ученый-физик. Майеру на момент путешествия было всего 28 лет, во время стоянки корабля в тропическом регионе при кровопускании он наблюдал, что багрово-красная кровь, вытекающая во время процедуры у жителей холодной Европы, в тропиках напоминала алую артериальную…
07 августа 2019
Майер предположил, что кровь не меняет цвет, поскольку организму в тропическом климате нет необходимости тратить кислород на поддержание
температуры тела. Вернувшись на родину, перед тем как сформулировать закон сохранения механической энергии, Майер продолжил опыты с открытыми на то время разновидностями энергии:
- кинетической,
- потенциальной,
- внутренней,
- механической;
…и смог определить, в чем заключается закон сохранения механической энергии.
«Тепло, электричество и перемещение представляют собою феномены, которые могут быть сведены к одной силе, измеряются друг другом и переходят друг в друга по определенным законам» — излагал в своей научной работе Майер.
Английский физик Джеймс Джоуль, чье имя носит единица измерения энергии, и германский естествоиспытатель Герман Гельмгольц несколькими годами позже также
описали закон сохранения энергии.
Физика. 8 класс. Учебник.
Учебник соответствует Федеральному государственному образовательному стандарту основного общего образования. Большое количество красочных иллюстраций, разнообразные вопросы и задания, а также дополнительные сведения и любопытные факты способствуют эффективному усвоению учебного материала.
Купить
Кинетическая и потенциальная энергия
Энергия тела — физическая величина, определяющая работу наблюдаемого тела или системы тел за бесконечно долгое время.
В изучении механических явлений рассматривают потенциальную и кинетическую энергии.
- Единица энергии в СИ 1 Джоуль (Дж).
Кинетическая энергия — энергия, которой обладает тело в движении (вращении, перемещении в пространстве).
Футбольный мяч, летящий в ворота, летящая в цель стрела, выпущенная метким лучником, едущие с горы сани с сидящим в них хохочущим ребенком — все они во время движения характеризуются кинетической энергией.
Кинетическая энергия напрямую зависит от массы тела и скорости перемещения.
Формула кинетической энергии Ек = mv2/2
Где где m — масса объекта;
v — скорость перемещения объекта в конкретной точке.
Потенциальная энергия. Само по себе тело потенциальной энергией не обладает. Этот вид энергии характеризует взаимосвязь элементов объекта или двух отдельных тел в пространстве.
Стоящие на вершине холма санки, стрела, вложенная лучником в натянутую тетиву, ядро в стволе средневековой пушки — пример объекта, обладающего потенциальной энергией.
Потенциальная энергия бывает положительной или отрицательной относительно определенного условного нулевого уровня, принятого для системы координат:
- сила тяжести,
- сила упругости,
- архимедова сила
Потенциальная энергия объекта зависит от приложенных к нему сил.
Если оценивать расположение объекта в отношении уровня Земли, то потенциальная энергия объекта на поверхности планеты принимается за ноль.
Уравнение Еп = mɡh поможет рассчитать потенциальную энергию на высоте h:
где m — масса тела;
ɡ – ускорение свободного падения;
h — высота центров масс объектов относительно поверхности планеты;
ɡ = 9,8 м/с2
Потенциальная энергия упруго деформированного объекта (пружины) рассчитывается согласно уравнению:
Еп = k·(∆x)2/2,
где k — коэффициент жёсткости,
∆x — изменение длины объекта вследствие его сжатия или растяжения.
Подробно различные виды потенциальной энергии разбираются на странице 131 учебника «Физика 10 кл. под редакцией Касьянова В. А.»
Физика. 9 класс. Учебник.
Учебник отличаются качественным современным оформлением, в нём приводятся многочисленные слайды и микрофотографии. Выполняя проблемные, поисковые и исследовательские задания, школьники не только активно усваивают материал, но и учатся мыслить, искать и анализировать информацию из разных источников, в том числе из интернета. Особое внимание уделяется практическим заданиям: ученикам предлагается проводить опыты, конструировать модели, разрабатывать проекты.
Купить
Закон превращения и сохранения энергии
Суммарное число значений потенциальной и кинетической энергий объекта обозначают как механическая энергия. Для каждого конкретного объекта механическая энергия определяется не выбором системы отсчета, в которой рассчитывают скорость движения исследуемого объекта, а установлением уровня условного нуля для всех видов потенциальных энергий, определенных у данного объекта.
Механическая энергия определяет свойство объекта (системы объектов) совершать работу за счет изменения скорости перемещения объекта или изменения расположения взаимодействующих объектов относительно друг друга.
Сформулируем закон сохранения механической энергии с помощью математического уравнения:
Еk1 + Еп1 = Еk2 + Еп2
Глядя на представленную формулу видно, что энергия не появляется из ниоткуда и не исчезает в неизвестном направлении; лишь происходит преобразование одной разновидности в другую или переход между взаимодействующими объектами.
В изолированной или закрытой системе, т.е. системе, на которую не оказывают влияния силы извне или их возможно игнорировать, энергетический обмен с внешней средой не происходит, и внутренняя энергия объекта не изменяется. В ней могут происходить лишь превращения потенциальной энергии в кинетическую и наоборот. В учебнике «Физика. 10 класс» под редакцией В. А. Касьянова на портале LECTA разобраны примеры задач на закон сохранения энергии.
#ADVERTISING_INSERT#
Одним из самых важных законов механики является закон сохранения энергии. Применительно к механике к названию добавляют логичную приписку “механической”. Стоит отметить, что закон сохранения работает в природе повсеместно. Относится это не только к энергии, но и скажем, к веществу. Тематика входит в раздел #классическая механика .
Прежде, чем говорить о сохранении энергии, рационально вспомнить что вообще такое энергия.
Здесь мы встречаемся с первым парадоксом. Никто до сих пор толком и не понял до конца, что такое энергия. Про это мы подробно писали в этом материале. Но более или менее доходчивое определение есть.
Энергия (в переводе с греческого мощь) это скалярная физическая величина, являющаяся мерой форм движения и взаимодействия материи или мерой перехода движения материи из одних форм в другие.
В целом-то, определение понятное и логичное. Нужно было каким-то образом описать, сколько “воздействия” один объект может передать другому. Для этого ввели данный термин.
В случае перехода к механике всё ещё проще. Нужно как-то охарактеризовать, сколько работы запасено в некоторой ситуации. Иначе не скажешь. Та самая висящая на веревке гиря прекрасный тому пример. Если веревку обрезать, то гиря может совершить работу. Значит, гиря обладает потенциальной энергией. Потенциальная энергия превратится впоследствии в кинетическую.
Механическая энергия – это способность тела совершать механическую работу.
Вот полетел камень, происходит превращение энергии и работа совершается.
Теперь вернемся к закону сохранения механической энергии.
Мы помним, что выделяется энергия потенциальная и энергия кинетическая. Потенциальная энергия фигурирует всегда, когда есть ситуации, аналогичные подвешенной гире. Кинетическая энергия – это энергия движения и она тоже есть всегда, когда происходит механическое движение. Подвешенная гиря, которая была срезана и начала движение, обладает уже кинетической энергией.
Из этих нехитрых примеров следует, что при механических воздействия энергия может неограниченное количество раз превращаться одна в другую. Потенциальная энергия переходит в кинетическую, а кинетическая переходит в потенциальную.
Вист кирпич на веревке и обладает потенциальной энергией. Веревку отрезают, кирпич летит и потенциальная энергия практически полностью превратилась в кинетическую. Упал кирпич на балкон и вновь обладает потенциальной энергией. Ведь он и дальше притягивается к земле, даже этажом ниже своего прежнего расположения.
Когда речь идёт о механической энергии важно понимать, что всегда рассматривается сумма механической и потенциальной энергий.
Рассуждения же о превращении энергии одна в другую подталкивают к мысли, что на самом-то деле энергия не появляется и не пропадает. Она просто превращается из одной формы энергии в другую. И браво, коллеги, мы пришли к закону сохранения механической энергии.
Закон сохранения и превращения энергии гласит, что энеpгия ниоткуда не возникает и никуда не пропадает. Энергия лишь переходит из одного вида в другой или от одного тела к другому.
Как вы заметили, слово “механической” тут отсутствует. Этот закон справедлив не только для механики. Он работает во всей нашей вселенной. Во всех областях физики и во всех сферах нашей жизни. Но применительно к механике закон сохранения энергии учитывает преимущественно кинетическую энергию тела, потенциальную энергию тела и иногда ещё внутреннюю энергию тела (если происходит передача энергии движения в нагрев и т.п.)
Теперь посмотрим, как сформулирован закон сохранения механической энергии в книгах:
В замкнутой и консервативной системе тел полная механическая энергия сохраняется: ΔЕ = 0 или Е потенциальная 1 + Е кинетическая 1 = Е потенциальная 2 + Е кинетическая 2
Почему замкнутой? Потому что если система не замкнутая, то она будет обмениваться энергией с другими участниками процесса и энергия в итоге рассеивается.
Скажем, запустили мы всем известные шарики для демонстрации закона сохранения импульса. Они качаются и передают друг другу энергию в одной замкнутой системе. Замкнутая система тут – это рама с нитями и сами шарики. Будь система не замкнутая, шарики должны были бы бить, скажем, по внешней стенке.
Почему консервативная и что это значит? Потому что если на систему воздействуют внешние силы, то они внесут свой вклад в процесс и уравнение, где общее изменение энергии равно нулю уже будет несправедливым.
Все действующие на систему внешние и внутренние непотенциальные силы не должны совершать работы, а все потенциальные силы должны быть стационарны. Это и будет консервативная система.
Следовательно, если рассматривать систему, где происходит механическое движение и подул ветер, который заставил тело получить внешнюю энергию, уже не консервативная. Модель движения автомобиля по дороге далеко не консервативная.
Правда тут возникает один интересный вопрос…Часто обозначенные выше обстоятельства воспринимаются как те, которые мешают работать закону сохранения энергии.
Обратите внимание, что закон сохранения энергии работает всегда. Вне зависимости от того, консервативная ли система и замкнутая ли она. Только вот записать тогда его в форме, привычной нам из школьного учебника уже не получится. Реальная картина будет намного сложнее. Приведенная формулировка закона сохранения механической энергии используется для упрощения ситуации.
Так, простой пример с падением срезанной с веревки гири на пол можно значительно усложнить. Гиря висела на веревке, обладала потенциальной энергией. Веревку отрезали. Потенциальная энергия должна была полностью передаться падающей гири и превратиться в кинетическую, но мы не учли, что была ещё веревка, которая тоже получила часть этой энергии. Пока гиря падала, она воздействовала на воздух и испытывала трение. Нагрелись воздух и гиря. При падении она частично сломала пол, на который упала и перешла во внутреннюю энергию. И пусть всё это значения с приставкой микро-, но реальная картина должна учитывать всё это. Именно поэтому прыгающий мяч рано или поздно остановится.
Отсюда было логично предложено упрощать подобные взаимодействия и рассматривать гипотетические консервативные и замкнутые системы.
