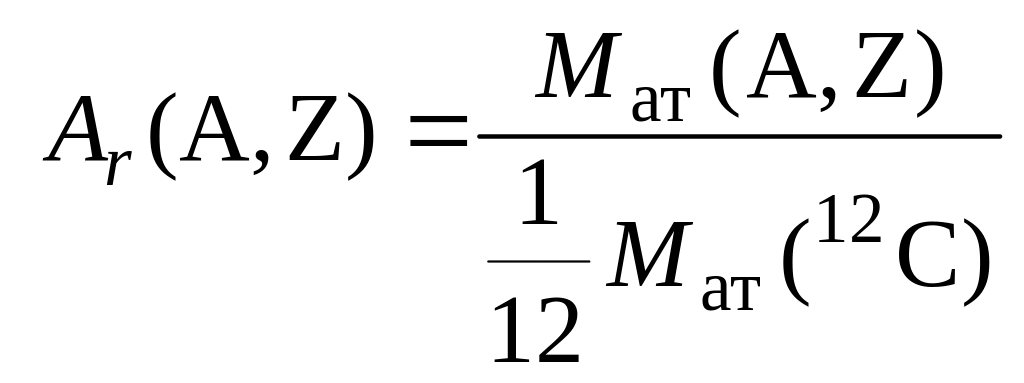Заряд ядра в кулонах как найти

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

Ядро
имеет положительный электрический
заряд, который образуют протоны. Число
протонов Z называют зарядом
ядра, подразумевая, что он равен величине
Ze Кл,
где е
= 1,602 10^–19
Кл (4,810^–10
CГCЕ ед.)
– абсолютная величина элементарного
электрического заряда.

Заряд
ядра был определен в 1913 г. Мозли, который
измерил с помощью дифракции на кристаллах
длину λ волны характеристического
рентгеновского излучения для ряда
химических элементов, следующих друг
за другом в периодической системе
элементов. Измерения показали, что λ
изменяется дискретным образом от
некоторой целой величины Z,
которая совпадает с порядковым номером
элемента и изменяется на единицу при
переходе от элемента к соседнему элементу
в периодической системе, а для водорода
равна единице. Мозли интерпретировал
эту величину как заряд ядра и установил,
что (закон Мозли):

где a и b
– константы для данной серии рентгеновского
излучения и не зависят от элемента.

Закон Мозли
определяет заряд ядер химического
элемента косвенным образом. Прямые
опыты по измерению заряда ядер на основе
закона Кулона были выполнены Чедвиком
в 1920 г. В 1911 г. Резерфорд, используя закон
Кулона, получил формулу

к
оторая
позволила объяснить экспериментальные
результаты по рассеянию α-частиц
на тяжелых ядрах, что, в конечном итоге,
привело в 1911 г. к открытию атомного ядра
и созданию ядерной модели атома. В
формуле (1.2.2): N – количество α-частиц,
падающих в единицу времени на рассеиватель;
dN – количество
рассеянных в единицу времени α-частиц
в телесный угол dΩ
под углом θ; Ze
и n – заряд ядер
рассеивателя и их концентрация; v
и m_α
– скорость и масса α-частиц.
Схема опыта Чедвика приведена на рис.
1.2.1. Рассеиватель α-частиц в виде кольца
(заштриховано на рис 1.2.1) размещался
сносно и на равных расстояниях между
источником И
и детектором α-частиц
Д.
При измерении количества dN
рассеянных α-частиц
отверстие в кольце закрывалось экраном,
который поглощал прямой пучок α‑частиц
из источника в детектор. Детектор
регистрировал только α‑частицы,
рассеянные в телесный угол dΩ
под углом


к падающему пучку α-частиц.
Затем кольцо перекрывалось экраном с
отверстием, и измерялась плотность тока
α-частиц в
точке расположения детектора. Используя
полученные данные, рассчитывалось
количество N α‑частиц,
падающих на кольцо в единицу времени.
Таким образом, если известна энергия
α-частиц,
испускаемых источником, без труда
определяется величина Z
в формуле (1.2.2). Некоторые из результатов,
полученные Чедвиком, приведены в таблице
1.2.1 и не оставляют сомнений в справедливости
закона Мозли.

§

Таблица 1.2.1.

Результаты опытов
Чедвика

1.3. Масса ядра и масса атома

Масса
ядра является одной из важных характеристик.
Массу ядра нуклида данного состава
(А,Z) будем обозначать
М(А,Z) или М(^АХ),
а массу соответствующего нуклида М_ат.

В
ядерной физике, так же как и в атомной
физике, для измерения масс широко
используется атомная единица массы
(а.е.м.):

В этих
единицах:

масса протона m_p
= 1,672610^-24
г = 1,007825
а.е.м.;

масса нейтрона m_n
= 1,674910^-24
г = 1,008665 а.е.м.

Видно,
что 1 а.е.м. близка к массе нуклона, что
очень удобно.

Масса
электрона m_e
много меньше массы протона, m_p
/m_e
= 1836.

Масса
нуклида, выраженная в атомных единицах
массы,
является относительной величиной и
называется атомной
массой.
Атомная масса имеет специальное
обозначение А_r
(не путать с массовым числом А!).

Величина

называется избытком массы нуклида
и имеет большое значение в ядерной
физике. Формула (1.3.3) выражает различие
между понятиями атомной массы и массового
числа. Однако величина Δ(A,Z) <<
1 для всех нуклидов и поэтому даже для
самых легких ядер атомная масса примерно
равна массовому числу. Это послужило
одной из причин выбрать пару чисел (A,Z)
для идентификации состава ядра нуклида.

Связь
между массой любого тела и его энергией
покоя дается формулой:

где с =
2,99810¹⁰
см/с – скорость света в
вакууме. На этом основании в ядерной
физике для измерения массы, так же как
и энергии, часто используется единица
энергии электронвольт
(эВ) и производные от нее:

1 кэВ (килоэлектронвольт) = 10³
эВ

1 МэВ (мегаэлектронвольт)
= 10⁶ эВ

1 ГэВ (гигаэлектронвольт)
= 10⁹ эВ.

Напомним,
что 1 эВ –
изменение энергии элементарного заряда
е при
прохождении им разности потенциалов
равной 1 В.

Установим
соответствие между 1
а.е.м. и 1 эВ. Из формулы
(1.3.4):

1а.е.м.=
1,660510^-27(2,99810⁸)²
= 1,49210^-10 Дж,

а из
определения электронвольта:

1эВ = 1,60210^-191
= 1,60210^-19 Дж.

Таким
образом, из последних двух соотношений
следует, что

1 а.е.м. =
≈
931,5 МэВ,

и соответственно

m_p
=1,007825 а.е.м. = 1,672610^-24
г = 938,2 МэВ,

m_n
= 1,008665 а.е.м. =
1,674910^-24
г = 939,5 МэВ,

m_e=
5,485910^-4
а.е.м. = 9,109610^-28
г = 0,511 МэВ.

В
ядерной физике обычно пользуются не
массами ядер, а массами нуклидов. Это
вызвано тем, что невозможно измерить
непосредственно массу ядер без связанных
с ними электронов, за исключением
легчайших. Масса нуклида в пределах
точности современных методов измерения
масс равна сумме масс ядра и электронов,
составляющих атом, хотя в принципе масса
нуклида есть

г
де
Σq_i
– энергия связи электронов в атоме, Σq_i
≈ 13,6Z
эВ. Таким образом, энергия связи электронов
с ядром более чем в 10⁷ раз меньше
энергии покоя нуклида и практически не
влияет на его массу.

Массы
нуклидов определяют с помощью приборов,
которые называются масс-спектрометрами.
Схема устройства простейшего
масс-спектрометра изображена на рис.
1.3.1. В ионном источнике ИИ создаются
положительные ионы нуклидов, массу М_i
которых необходимо измерить. Ионы,
имеющие электрический заряд q_i,
поступают через отверстие в ускоряющее
электрическое поле, создаваемое
приложенной между ИИ и Д₁
разностью потенциалов U,
после прохождения которой ионы приобретают
кинетическую энергию

и со скоростью v
поступают в пространственно однородное
и постоянное магнитное поле с индукцией
В, вектор которой перпендикулярен
плоскости чертежа и направлен на
читателя. На ион в магнитном поле
действует сила Лоренца

которая создает центростремительное
ускорение v²/R,
направленное к точке О, под действием
которого ион будет двигаться по окружности
радиуса R. Таким
образом,

Исключив
из (1.3.6) и (1.3.8) скорость v,
находим, что величина массы иона

Окружность
нужного радиуса R
задается положением диафрагм Д₁,
Д₂ и Д₃ . Подбирая
величины U и В
добиваются того, чтобы пучок ионов
попадал на коллектор К, что фиксируется
по максимуму тока ионов на коллекторе.
Таким образом устанавливается, что ион
движется по окружности радиуса R
и вычисляется масса иона. Если известна
кратность ионизации то, вычитая из массы
иона известную суммарную массу электронной
оболочки, получают массу ядра.

Знаете ответ?

Основными характеристиками атомных ядер являются электрический заряд, масса, спин, энергия связи и так далее.

Заряд ядра

Ядро каждого из атомов обладает положительным зарядом. В качестве носителя положительного заряда выступает протон. По той причине, что заряд протона численно эквивалентен заряду электрона e, можно записать, что заряд ядра элемента равен +Ze (Z выражает собой целое число, которое указывает на порядковый номер химического элемента в периодической системе химических элементов Д. И. Менделеева). Значение Z также характеризует число протонов, входящих в состав ядра и количество электронов в атоме. Именно из-за этого его определяют как атомный номер ядра. Электрический заряд представляет собой одну из основных характеристик атомного ядра, от которой зависят оптические, химические и иные свойства атомов.

Масса ядра

Существует также другая значимая характеристика ядра, а именно масса. Массу атомов и ядер принято выражать в атомных единицах массы (а.е.м.), в качестве атомной единицы массы выступает 112 массы нуклида углерода C612:

где NA=6,022·1023 моль-1 обозначает число Авогадро.

Кроме того, есть другой способ выражения атомной массы: исходя из соотношения Эйнштейна E=mc2, ее выражают в единицах энергии. По той причине, что масса протона mp=1.00728 а.е.м.=938,28 МэВ, масса нейтрона mn=1.00866а.е.м.=939,57МэВ, а масса электрона me=5,49⋅10-4 а.е.м.=0,511МэВ,

Из приведенных выше значений видно, что масса электрона несущественно мала, если сравнивать ее с массой ядра, поэтому масса ядра практически эквивалентна массе всего атома и отлична от целых чисел.

Масса ядра, которая выражается в а.е.м. и округляется до целого числа носит название массового числа и обозначается с помощью буквы A. Она характеризует количество нуклонов, находящихся в составе ядра.

Количество нейтронов в ядре эквивалентно N=A−Z. В качестве обозначения ядер используют символ XZA, в котором X определяется как химический символ этого элемента.

Атомные ядра, обладающие одинаковым числом протонов, однако при этом отличающимися друг от друга массовыми числами, носят название изотопов.

В некоторых элементах количество стабильных и нестабильных изотопов достигает десятков, в качестве примера, уран обладает 14 изотопами: от U92227 до U92240. Большая часть химических элементов, которые существуют в природе, являются смесью нескольких изотопов. Как раз наличие изотопов объясняет следующее явление: некоторые природные элементы обладают массой, которая является отличной от целых чисел. В качестве примера рассмотрим природный хлор, который состоит из 75% C1735l и 24% C1737l, а его атомная масса эквивалентна 35,5 а.е.м. В большей части атомов, исключая водород, изотопы обладают практически равными физическими и химическими свойствами. Однако, за своими, исключительно ядерными свойствами, изотопы значительно отличаются друг от друга. Какие-то из них могут представлять собой стабильные изотопы, а другие – радиоактивные.

Ядра с эквивалентными массовыми числами, но отличающимися значениями Z носят название изобар, в качестве примера, A1840r, C2040a.

Ядра с одинаковым числом нейтронов определяют как изотоны.

Среди легких ядер встречаются и так называемые «зеркальные» пары ядер. Это такие пары ядер, в которых числа Z и A−Z меняются местами. В качестве примера подобных ядер можно привести C613 и N713 или H13 и H23e.

Размер атомного ядра

Принимая форму атомного ядра приблизительно сферической, мы имеем возможность ввести понятие его радиуса R. Обратим внимание на то, что в некоторых ядрах есть небольшое отклонение от симметрии в распределении электрического заряда. Более того, атомные ядра представляют собой не статические, а динамические системы, и понятие радиуса ядра нельзя представлять как радиус шара. Именно из-за этого факта, в качестве размеров атомного ядра нужно принимать ту область, в которой проявляются ядерные силы. В процессе создания количественной теории рассеивания α-частиц Э. Резерфорд исходил из тех предположений, что атомное ядро и α – частица взаимодействуют по закону Кулона, Другими словами из того, что электрическое поле вокруг ядра обладает сферической симметрией.

Это работает в отношении α – частиц, обладающих достаточно малым значением энергии E. При этом частица не имеет возможности преодолеть кулоновский потенциальный барьер и в последствии не достигает области, в которой наблюдается действие ядерных сил. Одновременно с повышением энергии частицы до некоторого граничного значения Eгр, α-частица достигает данной границы. В таком случае в рассеянии α-частиц возникает некоторое отклонение от формулы Резерфорда.

Опытным путем было определено, что радиус R ядра является зависимым от числа нуклонов, которые входят в состав ядра.

Размеры ядер определяют экспериментальным путем по рассеянию протонов, быстрых нейтронов или же электронов высоких энергий. Существует также целый список иных косвенных способов получения значений размеров ядер. Они основываются:

• на связи времени жизни α – радиоактивных ядер с энергией выпущенных ими α – частиц;
• на оптических свойствах, носящих название мезоатомов, в которых один из электронов временно захвачен мюоном;
• на сравнении энергий связи парных зеркальных атомов.

Данные способы подтверждают эмпирическую зависимость R=R0A1/3, а также благодаря таким измерениям определено значение постоянной R0=1,2-1,5·10-15 м. Обратим свое внимание также на тот факт, что за единицу расстояний в атомной физике и физике элементарных частиц принимают единицу измерения «ферми», которая равняется 10-15 м 1 ф=10-15 м. Радиусы атомных ядер определяются их массовым числом и находятся в промежутке от 2·10-15 до 10-14 м. Если из формулы R=R0A1/3 выразить R0 и записать его в следующем виде 4πR33A=const, то можно заметить, что на каждый нуклон приходится примерно одинаковый объем. Из данного факта можно сделать вывод о том, что плотность ядерного вещества для всех ядер так же приблизительно одинакова. Как можно заметить, плотность ядерного вещества довольно велика. Этот факт основывается на действие ядерных сил.

Энергия связи. Дефект масс ядер

Величину ∆m, что определяет разницу масс между массой нуклонов, которые формируют ядро, и массой ядра, называют дефектом массы ядра.

Важные сведения о свойствах ядра могут быть получены даже при отсутствии знаний о подробностях взаимодействия между нуклонами ядра, на основании закона сохранения энергии и закона пропорциональности массы и энергии. Поскольку в результате каждого изменения массы ∆m происходит соответствующее изменение энергии ∆E(∆E=∆mc2), то при образовании ядра выделяется некоторое количество энергии. Исходя из закона сохранения энергии можно сделать вывод о том, что ровно такое же количество энергии необходимо для того, чтобы разделить ядро на составляющие его элементы, другими словами отдалить нуклоны друг от друга на такие расстояния, при которых взаимодействия между ними не происходит. Данную энергию определяют как энергию связи ядра.

Заметим, что данная формула довольно неудобная в применении, так как в таблицах приводиться не массы ядер, а массы, которые относятся к массам нейтральных атомов. По этой причине ради удобства вычислений формулу преобразуют таким образом, чтобы в нее входили не массы атомов, а массы ядер. Для достижения этой цели в правой части формулы добавим и отнимем массу Z электронов (me). В таком случае Eсв=Zmp+me+A-Zmn-mя+Zmec2=ZmH11+A-Zmn-mac2 — масса атома водорода, ma — масса атома.

В ядерной физике энергию зачастую выражают в мегаэлектрон-вольтах (МэВ). Если речь идет о практическом применении ядерной энергии, то ее измеряют в джоулях. В случае сравнения энергии двух ядер используют массовую единицу энергии — соотношение между массой и энергией (E=mc2). Массовая единица энергии (le) равняется энергии, что соответствует массе в одну а.е.м. Она равняется 931,502 МэВ.

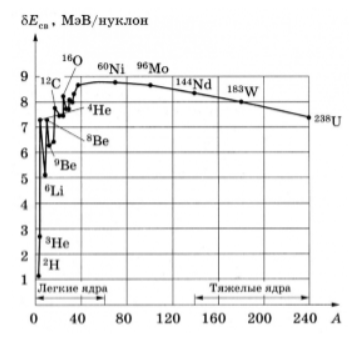
Рисунок 1

Кроме энергии, важное значение имеет удельная энергия связи ядра — энергия связи, которая припадает на один нуклон: ω=Ecв/A. Эта величина меняется сравнительно медленно по сравнению со сменой массового числа A, имея почти постоянную величину 8.6 МэВ в средней части периодической системы и уменьшается до ее краев.

Дефект массы

Энергия связи в МэВ: Eсв=∆m·931,502=0,030359·931,502=28,3 МэВ;

Удельная энергия связи: ω=EсвA=28,3 МэВ4≈7.1 МэВ.