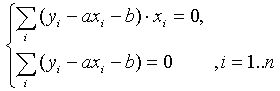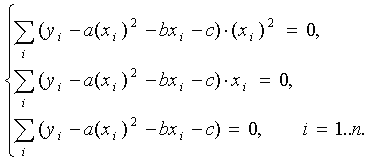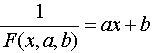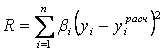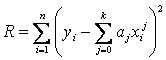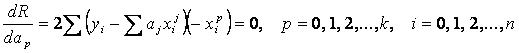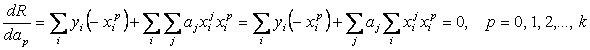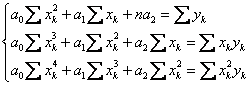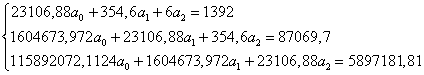3.1.Постановка
задачи аппроксимации функции одной
переменной
Пусть
в результате измерений в процессе опыта
получено табличное задание некоторой
функции f(х),выражающей связь между
двумя географическими параметрами:
(1)
|
х |
x1 |
х2 |
… |
xn |
|
f(x) |
y1 |
у2 |
… |
yn |
Конечно,
можно найти формулу, выражающую эту
зависимость аналитически, применив
метод интерполяции. Однако, совпадение
значений полученного аналитического
задания функции в узлах интерполяции
с имеющимися эмпирическими данными
часто может вовсе не означать совпадение
характеров поведения исходной и
интерполирующей функции на всем интервале
наблюдения. Кроме того, табличная
зависимость географических показателей
всегда получается в результате измерений
различными приборами, имеющими
определенную и не всегда достаточно
малую погрешность измерения. Требование
точного совпадения значений приближающей
и приближаемой функций в узлах является
тем более неоправданным, если значения
функции f(х),полученные в результате
измерений уже сами являются приближенными.
Задача
аппроксимации функции одной переменной
с самого начала обязательно учитывает
характер поведения исходной функции
на всем интервале наблюдений. Формулировка
задачи выглядит следующим образом.
Функция у= f(х)задана таблицей (1).
Необходимо найти функцию заданного
вида:
y=F(x)(2)
которая
в точках x1, x2,
…, xnпринимает значения,
как можно более близкие к табличнымy1,
y2, …, yn.
На
практике вид приближающей функции чаще
всего определяют путем сравнения вида
приближенно построенного графика
функции у= f(х)с графиками известных
исследователю функций, заданных
аналитически (чаще всего простых по
виду элементарных функций). А именно,
по таблице (1) строится точечный графикf(x),затем проводится плавная кривая,
по возможности наилучшим образом
отражающая характер расположения точек.
По полученной таким образом кривой на
качественном уровне устанавливается
вид приближающей функции.
Рассмотрим
рисунок 6.
Рис.
6
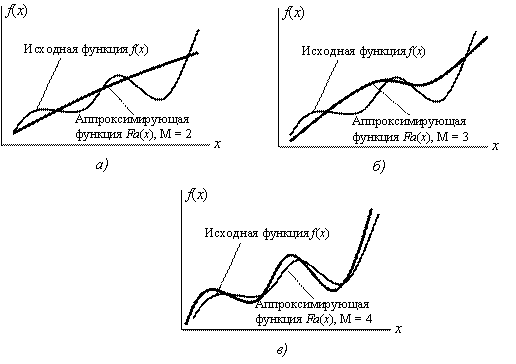
На
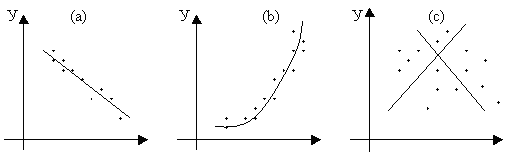
рисунке 6 изображены три ситуации:
-
На
графике (а) взаимосвязь х
и у
близка к линейной; прямая линия здесь
близка к точкам наблюдений, и последние
отклоняются от нее лишь в результате
сравнительно небольших случайных
воздействий. -
На
графике (b) реальная взаимосвязь величин
х
и у
описывается нелинейной функцией, и
какую бы мы ни провели прямую линию,
отклонение точек наблюдения от нее
будет существенным и неслучайным. В то
же время, проведенная ветка параболы
достаточно хорошо отражает характер
зависимости между величинами. -
На
графике (с) явная взаимосвязь между
переменными х
и
у
отсутствует; какую бы мы ни выбрали
формулу связи, результаты ее параметризации
будут здесь неудачными. В частности,
обе выбранные прямые одинаково плохи
для того, чтобы делать выводы об ожидаемых
значениях переменной у
по значениям переменной х.
Следует
заметить, что строгая функциональная
зависимость для таблицы исходных данных
наблюдается редко, ибо каждая из
участвующих в ней величин может зависеть
от многих случайных факторов. Однако
формула (2) (ее называют эмпирической
формулой или уравнением регрессии унах) интересна тем, что позволяет
находить значения функцииfдля
нетабличных значенийх, “сглаживая”
результаты измерений величиныу,
т.е. на всем интервале изменениях.
Оправданность такого подхода определяется
в конечном счете практической полезностью
полученной формулы.
3.2.
Метод наименьших квадратов
Через
имеющееся “облако” точек всегда
можно попытаться провести линию
установленного вида, которая является
наилучшей в определенном смысле среди
всех линий данного вида, то есть
“ближайшей” к точкам наблюдений
по их совокупности. Для этого определим
вначале понятие близости линии к
некоторому множеству точек на плоскости.
Меры такой близости могут быть различными
[13]. Однако, любая разумная мера должна
быть, очевидно, связана с расстоянием
от точек наблюдения до рассматриваемой
линии (задаваемой уравнением y=F(x)).
Предположим,
что приближающая функция F(x)в точкахх1, x2, …, xnимеет значенияy1,
y2, …, yn.
Часто в качестве критерия близости
используется минимум суммы квадратов
разностей наблюдений зависимой переменнойyiи теоретических,
рассчитанных по уравнению регрессии
значенийyi. Здесь
считается, чтоyiиxi– известные данные наблюдений, аF–
уравнение линии регрессии с неизвестными
параметрами (формулы для их вычисления
будут приведены ниже). Метод оценивания
параметров приближающей функции,
минимизирующий сумму квадратов отклонений
наблюдений зависимой переменной от
значений искомой функции, называетсяметодом наименьшихквадратов
(МНК)илиLeast Squares Method (LS).
Итак,
задачу приближения функции f теперь
можно сформулировать следующим образом:
для функцииf, заданной таблицей
(1), найти функциюFопределенного
вида так, чтобы сумма квадратов Ф была
наименьшей.
Рассмотрим
метод нахождения приближающей функции
в общем виде на примере аппроксимирующей
функции с тремя параметрами:
(3)
Пусть
F(xi, a, b, c) = yi,
i=1, 2, …, n.Сумма квадратов разностей
соответствующих значенийfиFбудет иметь вид:
(4)
Эта
сумма является функцией Ф(а, b, c)трех
переменных (параметровa, bиc).
Задача сводится к отысканию ее минимума.
Используем необходимое условие
экстремума:
Получаем
систему для определения неизвестных
параметров a, b, c.

Решив
эту систему трех уравнений с тремя
неизвестными относительно параметров
a, b, c,мы и получим конкретный вид
искомой функцииF(x, a, b, c).Как видно
из рассмотренного примера, изменение
количества параметров не приведет к
искажению сущности самого подхода, а
выразится лишь в изменении количества
уравнений в системе (5).
Естественно
ожидать, что значения найденной функции
F(x, a, b, c)в точкахх1,
x2, …, xn, будут
отличаться от табличных значенийy1,
y2, …, yn. Значения
разностейyi-F(xi,a,
b, c)=e i (i=1, 2, …, n)называются
отклонениями измеренных значенийyот вычисленных по формуле (3). Для найденной
эмпирической формулы (2) в соответствии
с исходной таблицей (1) можно, следовательно
найти
сумму
квадратов отклонений
,
которая в соответствии с методом
наименьших квадратов для заданного
вида приближающей функции (и найденных
значений параметров) должна быть
наименьшей. Из двух разных приближений
одной и той же табличной функции, следуя
методу наименьших квадратов, лучшим
нужно считать то, для которого сумма
(4) имеет наименьшее значение.
В
экспериментальной практике в качестве
приближающих функций в зависимости от
характера точечного графика fчасто
используются приближающие функции с
двумя параметрами:
Очевидно,
что когда вид приближающей функции
установлен, задача сводится только к
отысканию значений параметров.
3.3.
Нахождение приближающей функции в виде
основных элементарных функций
Рассмотрим
наиболее часто встречающиеся в
практических исследованиях эмпирические
зависимости.
3.3.1.
Линейная функция (линейная регрессия).
Начальным пунктом анализа зависимостей
обычно является оценка линейной
зависимости переменных. Следует при
этом учитывать, однако, что “наилучшая”
по методу наименьших квадратов прямая
линия всегда существует, но даже наилучшая
не всегда является достаточно хорошей.
Если в действительности зависимостьy=f(x)является квадратичной, то ее не
сможет адекватно описать никакая
линейная функция, хотя среди всех таких
функций обязательно найдется “наилучшая”.
Если величиныхиувообще не
связаны, мы также всегда сможем найти
“наилучшую” линейную функциюy=ax+bдля данной совокупности наблюдений, но
в этом случае конкретные значенияаиbопределяются только случайными
отклонениями переменных и сами будут
очень сильно меняться для различных
выборок из одной и той же генеральной
совокупности.
Рассмотрим
теперь задачу оценки коэффициентов
линейной регрессии более формально.
Предположим, что связь между xиyлинейна и искомую приближающую функцию
будем искать в виде:
(6)
Найдем
частные производные по параметрам:
Подставим
полученные соотношения в систему вида
( 5 ):
Далее
имеем:
или,
деля каждое уравнение на n:
Введем
обозначения:

Тогда
последняя система будет иметь вид:

Коэффициенты
этой системы Mx , My
, Mxy , Mx2– числа, которые в каждой конкретной
задаче приближения могут быть легко
вычислены по формулам ( 7 ), гдеxi,
yi– значения из таблицы (1).
Решив систему ( 8 ), получим значения
параметровaиb, а следовательно,
и конкретный вид линейной функции ( 6 ).
Необходимым
условием для выбора линейной функции
в качестве искомой эмпирической формулы
является соотношение [38]:
3.3.2.
Квадратичная функция (квадратичная
регрессия). Будем искать приближающую
функцию в виде квадратного трехчлена:
(9)
Находим
частные производные:
Составим
систему вида (5):
После
несложных преобразований получается
система трех линейных уравнений с тремя
неизвестными a, b, c. Коэффициенты
системы, так же как и в случае линейной
функции, выражаются только через
известные данные из таблицы (1):

Здесь
использованы обозначения (7), а также
Решение
системы (10) дает значение параметров a,
bисдля приближающей функции
(9).
Квадратичная
регрессия применяется, если все выражения
вида у2 -2y1 +
y0 , y3 -2
y2 + y1 , y4
-2 y3 + y2
и т.д. мало отличаются друг от друга.
3.3.3.
Степенная функция (геометрическая
регрессия). Найдем теперь
приближающую функция в виде:
(11)
Предполагая,
что в исходной таблице ( 1) значения
аргумента и значения функции положительны,
прологарифмируем равенство ( 11) при
условии а>0:
(12)
Так
как функция Fявляется приближающей
для функцииf, функцияlnFбудет
приближающей для функцииlnf. Введем
новую переменнуюu=lnx; тогда, как
следует из (12),lnFбудет функцией отu:Ф(u).
Обозначим
(13)
Теперь
равенство (12) принимает вид:
(14)
т.е.
задача свелась к отысканию приближающей
функции в виде линейной. Практически
для нахождения искомой приближающей
функции в виде степенной (при сделанных
выше предположениях) необходимо проделать
следующее:
1.
по данной таблице ( 1 ) составить новую
таблицу, прологарифмировав значения xиyв исходной таблице;
2.
по новой таблице найти параметры АиВприближающей функции вида (14);
3.
использовав обозначения (13), найти
значения параметров aиmи
подставить их в выражение (11).
Необходимым
условием для выбора степенной функции
в качестве искомой эмпирической формулы
является соотношение [38]:
3.3.4.
Показательная функция. Пусть
исходная таблица (1) такова, что приближающую
функцию целесообразно искать в виде
показательной функции:
(15)
Прологарифмируем
равенство (15):
(16)
Приняв
обозначения (13), перепишем (16) в виде:
(17)
Таким
образом, для нахождения приближающей
функции в виде (15) нужно прологарифмировать
значения функции в исходной таблице
(1) и, рассматривая их совместно с исходными
значениями аргумента, построить для
новой таблицы приближающую функцию
вида ( 17). Вслед за этим в соответствии
с обозначениями ( 13) остается получить
значения искомых параметров aиbи подставить их в формулу (15).
Необходимым
условием для выбора показательной
функции в качестве искомой эмпирической
формулы является соотношение [38]:

3.3.5.
Дробно-линейная функция.Будем искать
приближающую функцию в виде:
(18)
Равенство
(18) перепишем следующим образом:
Из
последнего равенства следует, что для
нахождения значений параметров aиbпо заданной таблице (1) нужно
составить новую таблицу, у которой
значения аргумента оставить прежними,
а значения функции заменить обратными
числами, после чего для полученной
таблицы найти приближающую функцию
видаax+b. Найденные значения параметровaиbподставить в формулу ( 18).
Необходимым
условием для выбора дробно-линейной
функции в качестве искомой эмпирической
формулы является соотношение [38]:

3.3.6.
Логарифмическая функция. Пусть
приближающая функция имеет вид:
(19)
Легко
видеть, что для перехода к линейной
функции достаточно сделать подстановку
lnx=u. Отсюда следует, что для нахождения
значенийaиbнужно прологарифмировать
значения аргумента в исходной таблице
( 1 ) и, рассматривая полученные значения
в совокупности с исходными значениями
функции, найти для полученной таким
образом новой таблицы приближающую
функцию в виде линейной. Коэффициентыaиbнайденной функции подставить
в формулу (19).
Необходимым
условием для выбора логарифмической
функции в качестве искомой эмпирической
формулы является соотношение [38]:
.
3.3.7.
Гипербола. Если точечный график,
построенный по таблице (1), дает ветвь
гиперболы, приближающую функцию можно
искать в виде:
(20)
Для
перехода к линейной функции сделаем
подстановку

(21)
Практически
перед нахождением прибллижающей функции
вида ( 20) значения аргумента в исходой
таблице ( 1 ) следует заменить обратными
числами и найти для новой таблицы
приближающую функцию в виде линейной
вида ( 21). Полученные значения параметров
аиbподставить в формулу (20).
Необходимым
условием для выбора уравнения гиперболы
в качестве искомой эмпирической формулы
является соотношение [38]:
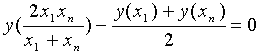
3.3.8.
Дробно-рациональная функция. Пусть
приближающая функция находится в виде:
(22)
Очевидно,
что

так
что задача сводится к случаю, рассмотренному
в предыдущем пункте. Действительно,
если в исходной таблице заменить значения
хиуих обратными величинами
по формулами
и
искать для новой таблицы приближающую
функцию видаu=bz+a, то найденные
значенияаиbбудут искомыми
для формулы (22).
Необходимым
условием для выбора дробно-рациональной
функции в качестве искомой эмпирической
формулы является соотношение [38]:
В
заключение отметим, что может получиться,
что не одна из рассмотренных выше функций
не приближает достаточно удовлетворительно
имеющиеся эмпирические данные. В таком
случае вид эмпирической кривой выбирают
исходя из каких-то других известных
данных о поведении функции. Иногда это
помогают сделать специальные компьютерные
программы аппроксимации экспериментальных
данных [38].
1
2
Воспользуемся программой на языке
Паскаль:
Листинг
в приложении
Результат
работы программы:
Vvedite
chislo eksperimentalnih tochek m>1
5
Vvedite
pari nacheniy xi,yi
1
7.1
2
6.1
3
4.9
4
4
5
3.1
empirichskaja
formula N4 d= 0.00577 k=-0.20105 b= 2.18070
Dlja
prodolgenija nagmite lubuyu klavishu
Из
предложенных вариантов программа
выбрала 4-ью формулу.
X=x
Y=ln
y
3
d=
0.00577
k=-0.20105
b=2.18070
Уравнение
прямой y=-0.20105*x+2.18070
4
A=e^b
B=e^k
y=A*B^k
a=8,794
B=0.818
y=8.850794*0.818
^x
|
1 |
7,2 |
7,193492 |
|
2 |
5,9 |
5,884276 |
|
3 |
4,9 |
4,813338 |
|
4 |
4 |
3,937311 |
|
5 |
3,2 |
3,22072 |
Задание
4
Вычислить
заданные интегралы по формулам
прямоугольников, трапеций и Симпсона,
если отрезок интегрирования разбит на
n=2 и n=4
равные части. Оценить погрешность
результата и сравнить приближенные
значения интеграла с точными.
Точное
значение данного интеграла 0,386294.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Аппроксимацией (приближением) функции называется нахождение такой функции
(аппроксимирующей функции), которая была бы близка заданной. Критерии близости функций
и
могут быть различные.
Основная задача аппроксимации — построение приближенной (аппроксимирующей) функции, в целом наиболее близко проходящей около данных точек или около данной непрерывной функции. Такая задача возникает при наличии погрешности в исходных данных (в этом случае нецелесообразно проводить функцию точно через все точки, как в интерполяций) или при желании получить упрощенное математическое описание сложной или неизвестной зависимости.
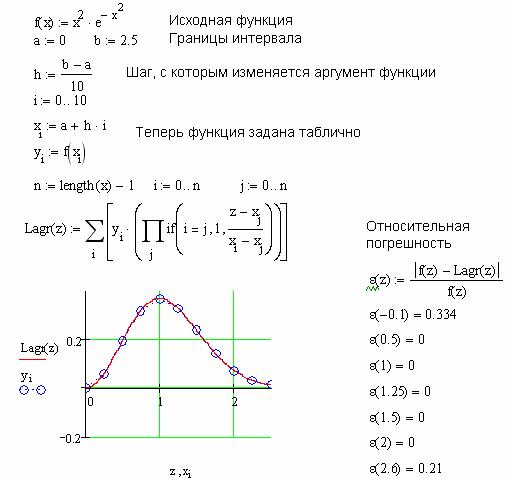
Рис. 3.6 Метод Лагранжа
Концепция аппроксимации
Близость исходной и аппроксимирующей функций определяется числовой мерой
— критерием аппроксимации (близости). Наибольшее распространение получил квадратичный критерий, равный сумме квадратов отклонений расчетных значений от “экспериментальных” (т.е. заданных), — критерий близости в заданных точках:
Здесь уi — заданные табличные значения функции; уiрасч — расчетные значения по аппроксимирующей функции; bi — весовые коэффициенты, учитывающие относительную важность i-и точки (увеличение b,. приводит при стремлении уменьшить R к уменьшению, прежде всего отклонения в i–й точке, так как это отклонение искусственно увеличено за счет относительно большого значения весового коэффициента).
Квадратичный критерий обладает рядом “хороших” свойств, таких, как дифференцируемость, обеспечение единственного решения задачи аппроксимации при полиномиальных аппроксимирующих функциях.
Другим распространенным критерием близости является следующий:
Этот критерий менее распространен в связи с аналитическими и вычислительными трудностями, связанными с отсутствием гладкости функции и ее дифференцируемости.
Выделяют две основные задачи:
1) получение аппроксимирующей функции, описывающей имеющиеся данные, с погрешностью не хуже заданной;
2) получение аппроксимирующей функции заданной структуры с наилучшей возможной погрешностью.
Чаще всего первая задача сводится ко второй перебором различных аппроксимирующих функций и последующим выбором наилучшей.
Метод наименьших квадратов
Метод базируется на применении в качестве критерия близости суммы квадратов отклонений заданных и расчетных значений. При заданной структуре аппроксимирующей функции уiрасч(х) необходимо таким образом подобрать параметры этой функции, чтобы получить наименьшее значение критерия близости, т.е. наилучшую аппроксимацию. Рассмотрим путь нахождения этих параметров на примере полиномиальной функции одной переменной:
Запишем выражение критерия аппроксимации при bi =1 (i=1, 2,…, n) для полиномиального уiрасч (х):
Искомые переменные аj можно найти из необходимого условия минимума R по этим переменным, т.е. dR / dар = 0 (для р =0, 1,2,…,k). Продифференцируем по ар (р — текущий индекс):
После очевидных преобразований (сокращение на два, раскрытие скобок, изменение порядка суммирования) получим
Перепишем последние равенства
Получилась система n+1 уравнений с таким же количеством неизвестных аj, причем линейная относительно этих переменных. Эта система называется системой нормальных уравнений. Из ее решения находятся параметры аj аппроксимирующей функции, обеспечивающие minR, т.е. наилучшее возможное квадратичное приближение. Зная коэффициенты, можно (если нужно) вычислить и величину R (например, для сравнения различных аппроксимирующих функций). Следует помнить, что при изменении даже одного значения исходных данных (или пары значений хi, уi, или одного из них) все коэффициенты изменят в общем случае свои значения, так как они полностью определяются исходными данными. Поэтому при повторении аппроксимации с несколько изменившимися данными (например, вследствие погрешностей измерения, помех, влияния неучтенных факторов и т.п.) получится другая аппроксимирующая функция, отличающаяся коэффициентами. Обратим внимание на то, что коэффициенты аj полинома находятся из решения системы уравнений, т.е. они связаны между собой. Это приводит к тому, что если какой-то коэффициент вследствие его малости захочется отбросить, придется пересчитывать заново оставшиеся. Можно рассчитать количественные оценки тесноты связи коэффициентов. Существует специальная теория планирования экспериментов, которая
позволяет обосновать и рассчитать значения хi, используемые для аппроксимации, чтобы получить заданные свойства коэффициентов (несвязанность, минимальная дисперсия коэффициентов и т.д.) или аппроксимирующей функции (равная точность описания реальной зависимости в различных направлениях, минимальная дисперсия предсказания значения функции и т.д.).
Рис. 3.7 Влияние степени аппроксимирующего полинома М на точность аппроксимации
В случае постановки другой задачи — найти аппроксимирующую функцию, обеспечивающую погрешность не хуже заданной, — необходимо подбирать и структуру этой функции. Эта задача значительно сложнее предыдущей (найти параметры аппроксимирующей функции заданной структуры, обеспечивающей наилучшую возможную погрешность) и решается в основном путем перебора различных функций и сравнения получающихся мер близости. Для примера на рис. 3.7 приведены для визуального сравнения исходная и аппроксимирующие функции с различной степенью полинома, т.е. функции с различной структурой. Не следует забывать, что с повышением точности аппроксимации растет и сложность функции (при полиномиальных аппроксимирующих функциях), что делает ее менее удобной при использовании.
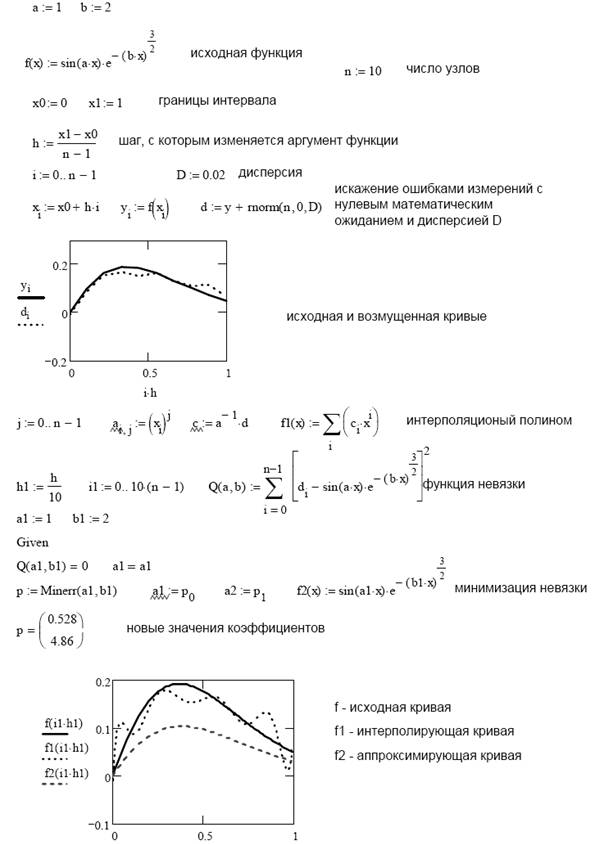
Рассмотрим решение задачи аппроксимации и интерполяции с шумом в
программе MathCAD (рисунок 3.8).
Пример 3.1. В ходе проведения эксперимента были получены данные, представленные в таблице 3.1. Необходимо способом наименьших квадратов подобрать для заданных значений x и y квадратичную функцию . Построить на одной координатной плоскости экспериментальные данные и аппроксимирующую функцию.
Таблица 3.1 Данные эксперимента
|
х |
80,5 |
77,0 |
70,8 |
56,7 |
39,7 |
29,9 |
|
у |
281 |
272 |
259 |
224 |
186 |
170 |
Решение. Для определения коэффициентов квадратичной функции построим дополнительную таблицу 3.2.
Таблица 3.2 Дополнительная таблица
|
|
|
|
|
|
|
|
|
|
1 |
80,5 |
6480,25 |
521660,13 |
41993640,0625 |
281 |
22620,5 |
1820950,25 |
|
2 |
77 |
5929 |
456533 |
35153041,0000 |
272 |
20944 |
1612688,00 |
|
3 |
70,8 |
5012,64 |
354894,91 |
25126559,7696 |
259 |
18337,2 |
1298273,76 |
|
4 |
56,7 |
3214,89 |
182284,26 |
10335517,7121 |
224 |
12700,8 |
720135,36 |
|
5 |
39,7 |
1576,09 |
62570,773 |
2484059,6881 |
186 |
7384,2 |
293152,74 |
|
6 |
29,9 |
894,01 |
26730,899 |
799253,8801 |
170 |
5083 |
151981,70 |
|
Σ |
354,6 |
23106,88 |
1604673,972 |
115892072,1124 |
1392 |
87069,7 |
5897181,81 |
Строим систему уравнений
В нашем случае она будет иметь вид:
Из полученной системы уравнений находим
Искомая зависимость
Строим график экспериментальных данных и найденной зависимости.
Рис.3.8 Аппроксимация и интерполяция в задаче с помехами
Если требуется построить зависимость в виде показательной функции , то необходимо составить систему:
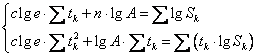
Для этого строится таблица
|
|
|
|
|
|
|
1 |
||||
|
… |
… |
… |
… |
… |
|
n |
||||
|
Σ |
Из системы 3.7 находим коэффициенты и
(необходимо выразить
).
Если требуется построить зависимость в виде степенной функции , то составляется система:
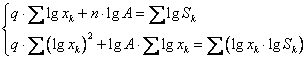
Для этого строится таблица
|
|
|
|
|
|
|
1 |
||||
|
… |
… |
… |
… |
… |
|
n |
||||
|
Σ |
Из системы 3.8 находим коэффициенты и
(необходимо выразить
).
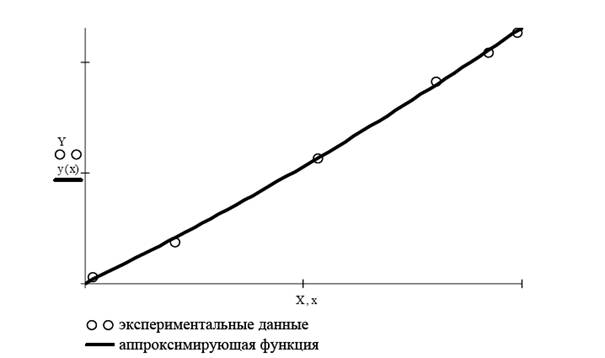
При обработке экспериментальных данных часто возникает необходимость аппроксимировать их линейной функцией.
Аппроксимацией (приближением) функции f(x) называется нахождение такой функции (аппроксимирующей функции) g(x), которая была бы близка заданной. Критерии близости функций могут быть различные.
В случае если приближение строится на дискретном наборе точек, аппроксимацию называют точечной или дискретной.
В случае если аппроксимация проводится на непрерывном множестве точек (отрезке), аппроксимация называется непрерывной или интегральной. Примером такой аппроксимации может служить разложение функции в ряд Тейлора, то есть замена некоторой функции степенным многочленом.
Наиболее часто встречающим видом точечной аппроксимации является интерполяция – нахождение промежуточных значений величины по имеющемуся дискретному набору известных значений.
Пусть задан дискретный набор точек, называемых узлами интерполяции, а также значения функции в этих точках. Требуется построить функцию g(x), проходящую наиболее близко ко всем заданным узлам. Таким образом, критерием близости функции является g(xi)=yi.
В качестве функции g(x) обычно выбирается полином, который называют интерполяционным полиномом.
В случае если полином един для всей области интерполяции, говорят, что интерполяция глобальная.
В случае если между различными узлами полиномы различны, говорят о кусочной или локальной интерполяции.
Найдя интерполяционный полином, мы можем вычислить значения функции между узлами, а также определить значение функции даже за пределами заданного интервала (провести экстраполяцию).
Аппроксимация линейной функцией
Пример реализации
Для примера реализации воспользуемся набором значений, полученных в соответствии с уравнением прямой
y = 8 · x — 3
Рассчитаем указанные коэффициенты по методу наименьших квадратов.
Результат сохраняем в форме двумерного массива, состоящего из 2 столбцов.
При следующем запуске программы добавим случайную составляющую к указанному набору значений и снова рассчитаем коэффициенты.
Реализация на Си
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
// Задание начального набора значений
double ** getData(int n) {
double **f;
f = new double*[2];
f[0] = new double[n];
f[1] = new double[n];
for (int i = 0; i<n; i++) {
f[0][i] = (double)i;
f[1][i] = 8 * (double)i – 3;
// Добавление случайной составляющей
f[1][i] = 8*(double)i – 3 + ((rand()%100)-50)*0.05;
}
return f;
}
// Вычисление коэффициентов аппроксимирующей прямой
void getApprox(double **x, double *a, double *b, int n) {
double sumx = 0;
double sumy = 0;
double sumx2 = 0;
double sumxy = 0;
for (int i = 0; i<n; i++) {
sumx += x[0][i];
sumy += x[1][i];
sumx2 += x[0][i] * x[0][i];
sumxy += x[0][i] * x[1][i];
}
*a = (n*sumxy – (sumx*sumy)) / (n*sumx2 – sumx*sumx);
*b = (sumy – *a*sumx) / n;
return;
}
int main() {
double **x, a, b;
int n;
system(“chcp 1251”);
system(“cls”);
printf(“Введите количество точек: “);
scanf(“%d”, &n);
x = getData(n);
for (int i = 0; i<n; i++)
printf(“%5.1lf – %7.3lfn”, x[0][i], x[1][i]);
getApprox(x, &a, &b, n);
printf(“a = %lfnb = %lf”, a, b);
getchar(); getchar();
return 0;
}
Результат выполнения
Запуск без случайной составляющей
Запуск со случайной составляющей
Построение графика функции
Для наглядности построим график функции, полученный аппроксимацией по методу наименьших квадратов. Подробнее о построении графика функции описано здесь.
Реализация на Си
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
#include <windows.h>
const int NUM = 70; // количество точек
LONG WINAPI WndProc(HWND, UINT, WPARAM, LPARAM);
double **x; // массив данных
// Определение коэффициентов линейной аппроксимации по МНК
void getApprox(double **m, double *a, double *b, int n) {
double sumx = 0;
double sumy = 0;
double sumx2 = 0;
double sumxy = 0;
for (int i = 0; i<n; i++) {
sumx += m[0][i];
sumy += m[1][i];
sumx2 += m[0][i] * m[0][i];
sumxy += m[0][i] * m[1][i];
}
*a = (n*sumxy – (sumx*sumy)) / (n*sumx2 – sumx*sumx);
*b = (sumy – *a*sumx) / n;
return;
}
// Задание исходных данных для графика
// (двумерный массив, может содержать несколько рядов данных)
double ** getData(int n) {
double **f;
double a, b;
f = new double*[3];
f[0] = new double[n];
f[1] = new double[n];
f[2] = new double[n];
for (int i = 0; i<n; i++) {
double x = (double)i * 0.1;
f[0][i] = x;
f[1][i] = 8 * x – 3 + ((rand() % 100) – 50)*0.05;
}
getApprox(f, &a, &b, n); // аппроксимация
for (int i = 0; i<n; i++) {
double x = (double)i * 0.1;
f[2][i] = a*x + b;
}
return f;
}
// Функция рисования графика
void DrawGraph(HDC hdc, RECT rectClient, double **x, int n, int numrow = 1) {
double OffsetY, OffsetX;
double MAX_X = 0;
double MAX_Y = 0;
double ScaleX, ScaleY;
double min, max;
int height, width;
int X, Y; // координаты в окне (в px)
HPEN hpen;
height = rectClient.bottom – rectClient.top;
width = rectClient.right – rectClient.left;
// Область допустимых значений X
min = x[0][0];
max = x[0][0];
for (int i = 0; i<n; i++) {
if (x[0][i] < min)
min = x[0][i];
if (x[0][i] > max)
max = x[0][i];
}
double temp = max – min;
MAX_X = max – min;
OffsetX = min*width / MAX_X; // смещение X
ScaleX = (double)width / MAX_X; // масштабный коэффициент X
// Область допустимых значений Y
min = x[1][0];
max = x[1][0];
for (int i = 0; i<n; i++) {
for (int j = 1; j <= numrow; j++) {
if (x[j][i] < min)
min = x[j][i];
if (x[j][i] > max)
max = x[j][i];
}
}
MAX_Y = max – min;
OffsetY = max*height / (MAX_Y); // смещение Y
ScaleY = (double)height / MAX_Y; // масштабный коэффициент Y
// Отрисовка осей координат
hpen = CreatePen(PS_SOLID, 0, 0); // черное перо 1px
SelectObject(hdc, hpen);
MoveToEx(hdc, 0, OffsetY, 0); // перемещение в точку (0;OffsetY)
LineTo(hdc, width, OffsetY); // рисование горизонтальной оси
MoveToEx(hdc, OffsetX, 0, 0); // перемещение в точку (OffsetX;0)
LineTo(hdc, OffsetX, height); // рисование вертикальной оси
DeleteObject(hpen); // удаление черного пера
// Отрисовка графика функции
int color = 0xFF; // красное перо для первого ряда данных
for (int j = 1; j <= numrow; j++) {
hpen = CreatePen(PS_SOLID, 2, color); // формирование пера 2px
SelectObject(hdc, hpen);
X = (int)(OffsetX + x[0][0] * ScaleX); // координаты начальной точки графика
Y = (int)(OffsetY – x[j][0] * ScaleY);
MoveToEx(hdc, X, Y, 0); // перемещение в начальную точку
for (int i = 0; i<n; i++) {
X = OffsetX + x[0][i] * ScaleX;
Y = OffsetY – x[j][i] * ScaleY;
LineTo(hdc, X, Y);
}
color = color << 8; // изменение цвета пера для следующего ряда
DeleteObject(hpen); // удаление текущего пера
}
}
// Главная функция
int WINAPI WinMain(HINSTANCE hInstance,
HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow) {
HWND hwnd;
MSG msg;
WNDCLASS w;
x = getData(NUM); // задание исходных данных
memset(&w, 0, sizeof(WNDCLASS));
w.style = CS_HREDRAW | CS_VREDRAW;
w.lpfnWndProc = WndProc;
w.hInstance = hInstance;
w.hbrBackground = CreateSolidBrush(0x00FFFFFF);
w.lpszClassName = “My Class”;
RegisterClass(&w);
hwnd = CreateWindow(“My Class”, “График функции”,
WS_OVERLAPPEDWINDOW, 500, 300, 500, 380, NULL, NULL,
hInstance, NULL);
ShowWindow(hwnd, nCmdShow);
UpdateWindow(hwnd);
while (GetMessage(&msg, NULL, 0, 0)) {
TranslateMessage(&msg);
DispatchMessage(&msg);
}
return msg.wParam;
}
// Оконная функция
LONG WINAPI WndProc(HWND hwnd, UINT Message,
WPARAM wparam, LPARAM lparam) {
HDC hdc;
PAINTSTRUCT ps;
switch (Message) {
case WM_PAINT:
hdc = BeginPaint(hwnd, &ps);
DrawGraph(hdc, ps.rcPaint, x, NUM, 2); // построение графика
EndPaint(hwnd, &ps);
break;
case WM_DESTROY:
PostQuitMessage(0);
break;
default:
return DefWindowProc(hwnd, Message, wparam, lparam);
}
return 0;
}
Результат выполнения
Аппроксимация с фиксированной точкой пересечения с осью y
В случае если в задаче заранее известна точка пересечения искомой прямой с осью y, в решении задачи останется только одна частная производная для вычисления коэффициента a.
В этом случае текст программы для поиска коэффициента угла наклона аппроксимирующей прямой будет следующий (имя функции getApprox() заменено на getApproxA() во избежание путаницы).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
// Задание начального набора значений
double ** getData(int n) {
double **f;
f = new double*[2];
f[0] = new double[n];
f[1] = new double[n];
for (int i = 0; i<n; i++) {
f[0][i] = (double)i;
f[1][i] = 8 * (double)i – 3;
// Добавление случайной составляющей
//f[1][i] = 8 * (double)i – 3 + ((rand() % 100) – 50)*0.05;
}
return f;
}
// Вычисление коэффициентов аппроксимирующей прямой
void getApproxA(double **x, double *a, double b, int n) {
double sumx = 0;
double sumx2 = 0;
double sumxy = 0;
for (int i = 0; i<n; i++) {
sumx += x[0][i];
sumx2 += x[0][i] * x[0][i];
sumxy += x[0][i] * x[1][i];
}
*a = (sumxy – b*sumx) / sumx2;
return;
}
int main() {
double **x, a, b;
int n;
system(“chcp 1251”);
system(“cls”);
printf(“Введите количество точек: “);
scanf(“%d”, &n);
x = getData(n);
for (int i = 0; i<n; i++)
printf(“%5.1lf – %7.3lfn”, x[0][i], x[1][i]);
b = 0;
getApproxA(x, &a, b, n);
printf(“a = %lfnb = %lf”, a, b);
getchar(); getchar();
return 0;
}
Результат выполнения программы поиска коэффициента угла наклона аппроксимирующей прямой при фиксированном значении b=0:
Назад: Алгоритмизация