Как вычислить ширину прямоугольника, если известна диагональ и высота?
©®oL™
Мыслитель
(6302),
закрыт
11 лет назад
Дополнен 11 лет назад
диагональ 10 см, высота 8 см. допустим так
Лучший ответ
Lex Lex
Ученик
(192)
11 лет назад
10^2=8^2+x^2 -> x=6 Теорема пифагора
Остальные ответы
Дарья Фоминова
Мастер
(1391)
11 лет назад
По теореме Пифагора: 10^2=8^2+ширина^2; Ширина=6
Дед Павел
Просветленный
(24528)
11 лет назад
А через синус 8/10 а потом косинус никак не катит
Александр Ломакин
Мастер
(1352)
11 лет назад
Указанный Вами прямоугольник делится диагональю на 2 “египетских” прямоугольных треугольника с соотношением сторон 3:4:5 (т. к. 2 известных стороны имеют отношение 10:5=5:4).Отсюда легко сразу ответить, что третья искомая сторона равна 6см.
Похожие вопросы
Его периметр
а будет выглядеть следующим образом: P = 2 x (a + b), или P = 2a + 2b. Из этой формулы следует, что найти длину второй стороны (b) можно с помощью следующей несложной операции: b = (P – 2a) : 2. Так, в нашем случае сторона b будет равна (20 – 2 х 7) : 2 = 3 см.
Теперь, зная длины обеих смежных сторон (a и b), вы легко сможете подставить их в формулу площади S = ab. В данном случае площадь прямоугольника
будет равна 7х3 = 21. Обратите внимание на то, что единицами измерения будут уже не сантиметры , а сантиметры квадратные, так как при умножении длин двух сторон единицы их измерения (сантиметры) вы тоже умножали друг на друга.
У нас есть два подхода для вас. Это вопрос алгебры, поэтому ученик должен быть удобным, представляя неизвестные значения с переменными. Таким образом, мы ищем два числа, которые при умножении дают 144 и при добавлении дают. В этот момент вы можете решить, должен ли ученик угадать, а затем проверить догадку, поместив ответы в два уравнения или продолжите аналитически. Для этого вопроса теперь легко угадать и проверить, но если вы хотите научить вашего ребенка более продвинутым методам, читайте дальше.
Вы можете обратиться к логике и сказать, что если вещь 1 такая же, как вещь 2, а вещь 3 – это то же самое, что и вещь 2, то вещь 1 должна быть такой же, как вещь. Это называется квадратичным выражением. Самый простой способ решить для фактической высоты – это фактор. Обратите внимание, что в этот момент мы эффективно используем «догадки» и еще раз: мы пытаемся найти два числа, которые умножились вместе, дают 144 и вместе добавляют.
Прямоугольник – плоская фигура, состоящая из четырех сторон и четырех прямых углов. Из всех фигур площадь
прямоугольника
приходится вычислять чаще других. Это и площадь
квартиры, и площадь
садового участка, и площадь
поверхности стола или полки. Например, чтобы просто оклеить комнату обоями, вычисляют площадь
ее прямоугольных стен.
Это долгий вопрос со многими шагами для студентки шестого класса, но продвинутый ученик многому научит видеть анализ. И другой, который не использует алгебру. Поскольку область является продуктом длины сторон, может оказаться полезным фактор 144 и увидеть какой может быть периметр, т.е. 48? Периметр, как вы знаете, представляет собой общее расстояние вдоль внешней стороны прямоугольника. Формула, используемая для расчета периметра.
Но дается, что площадь прямоугольника должна быть больше 18 кв. Это означает, что произведение длины и ширины должно быть больше, чем. Найдите соответствующие продукты, а затем создайте таблицу значений. Затем, наконец, нарисуем прямоугольник. Ниже перечислены вершины прямоугольника, и они также дают нам метки для вершин. Это будет прямо здесь. Итак, какова длина этой линии? Будет пять, независимо от того, какие единицы. Это будет равным 5. Мы перешли от точки к точке. Теперь они сказали, что это прямоугольник.
Инструкция
Кстати, из площади прямоугольника
можно легко вычислить площадь
прямоугольного треугольника . Достаточно достроить прямоугольный треугольник до прямоугольника
так, чтобы гипотенуза стала диагональю прямоугольника
. Тогда будет очевидно, что площадь
такого прямоугольника
равна произведению катетов треугольника, а площадь
самого треугольника, соответственно, равна половине произведения катетов.
Теперь, только для нашего удовлетворения, мы можем нарисовать весь прямоугольник. Мы на самом деле выясним все размеры этого прямоугольника. Кусок проволоки длиной 42 см согнут в форме прямоугольника, ширина которого вдвое превышает его длину. Найдите размеры прямоугольника.
Есть два способа подойти к этой проблеме. Во-первых, вы можете решить это с помощью набора уравнений. Первое уравнение ниже описывает периметр прямоугольника. Поскольку нам дается, что кусок проволоки длиной 42 см, а проволока образует внешнюю часть прямоугольника, который должен быть периметром.
Видео по теме
Частный случай параллелограмма – прямоугольник – известен только в геометрии Евклида. У прямоугольника
равны все углы, и каждый из них по отдельности составляет 90 градусов. Исходя из частных свойств прямоугольника
, а также из свойств параллелограмма о параллельности противолежащих сторон можно найти стороны
фигуры по заданным диагоналям и углу от их пересечения. Вычисление сторон прямоугольника
основывается на дополнительных построениях и применении свойств получаемых фигур.
Второе уравнение, ниже, описывает другое ограничение, данное в задаче. Он говорит, что ширина вдвое больше, поэтому мы можем перевести это в уравнение. У нас есть два уравнения с двумя неизвестными, поэтому мы просто решаем систему уравнений. В этом случае это довольно просто, потому что второе уравнение может быть непосредственно вставлено в первое, давая нам.
Поскольку ширина равна удвоенной длине, ширина должна быть 14. Мы знаем, что периметр равен 42, и добавление всех сторон вместе дает нам уравнение, которое выглядит как \. Задача с экстремальными значениями представляет собой проблему или проблему, в которой что-то под определенным условием максимизируется или минимизируется.
Инструкция
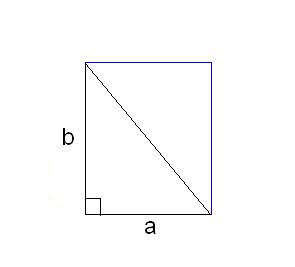
Буквой А отметьте точку пересечения диагоналей. Рассмотрите образованный построениями треугольник EFА. Согласно свойству прямоугольника
его диагонали равны и делятся пополам точкой пересечения А. Вычислите значения FА и EА. Так как треугольник EFА является равнобедренным и его стороны
EА и FА равны между собой и соответственно равны половине диагонали EG.
Из деревянной доски размером в половину квадрата с длиной стороны 1 м должен быть вырезан большой прямоугольник. Для чего целое число является продуктом предшественников и преемников наименьшим? Сформулируйте функцию, описывающую максимизацию. Какова область действия целевой функции?
Например, отрицательные длины бессмысленны. Это измененное вторичное условие теперь должно быть вставлено в целевую функцию. Многие студенты рассматривают геометрию, изучение форм и их пространственных свойств, одну из самых простых областей математики для поиска приложений в реальном мире. По периметру, определяемому как контурная мера двумерного объекта, является одной из основных концепций геометрии, и один из которых младшие студенты находят множество приложений в общих делах. Инженер-геодезист, который хочет оценить участок земли или фермер, который хочет поставить ограждение для защиты своего крупного рогатого скота, должен знать, как рассчитать периметр рассматриваемой площади.
Далее вычислите первую сторону EF прямоугольника
. Данная сторона является третьей неизвестной стороной рассматриваемого треугольника EFА. Согласно теореме косинусов по соответствующей формуле найдите сторону EF. Для этого подставьте в формулу косинусов полученные ранее значения сторон FА равна EА и косинус известного угла между ними α. Вычислите и запишите полученное значение EF.
Крайне важно, чтобы ученики осваивали идею периметра, прежде чем перейти к более сложным концепциям геометрии. Этот конкретный многоугольник определяется как фигура из четырех прямых углов и двух пар параллельных сторон. Стороны, которые образуют каждую пару, одинаковы, но пары не обязательно имеют одинаковое значение. Также необходимо знать точное значение одной стороны или, по крайней мере, значение одной стороны по отношению к другой стороне. В последнем случае замените первую неизвестную переменную уравнением, которое связывает ее со второй неизвестной переменной. Если сообщается только о периметре, нет возможности решить проблему.
. Эти правила называются качествами приверженности.
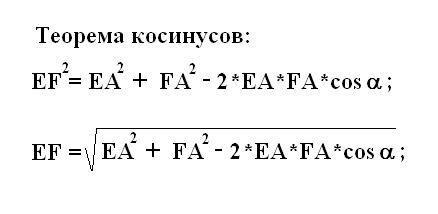
Найдите вторую сторону прямоугольника
FG. Для этого рассмотрите другой треугольник EFG. Он является прямоугольным, где известны гипотенуза EG и катет EF. Согласно теореме Пифагора найдите второй катет FG по соответствующей формуле.
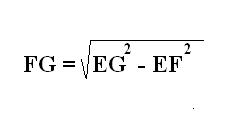
Чтобы доказать, что две фигуры являются конгруэнтными, достаточно найти изометрию, которая превращает одну фигуру в другую. Затем проиллюстрированы две конгруэнтные цифры. Просто переместите один из них и поверните, чтобы преобразовать одну фигуру в другую.
Ниже приведен пример цифр, которые не являются конгруэнтными. Вы не можете найти преобразование, которое держит расстояния, чтобы преобразовать одну фигуру в другую. 
Разделы конгруэнтны, если они равны. Две произвольные стороны квадрата конгруэнтны, потому что длины всех сторон квадрата одинаковы. В прямоугольнике только выбранные стороны конгруэнтны.
Прямоугольник относится к простейшим плоским геометрическим фигурам и является одним из частных случаев параллелограмма. Отличительная черта такого параллелограмма – прямые углы во всех четырех вершинах. Ограниченную сторонами прямоугольника
площадь
можно вычислить несколькими способами, используя размеры его сторон, диагонали и углы между ними, радиус вписанной окружности и т.д.
Круги конгруэнтны, если они имеют равные лучи. Два треугольника конгруэнтны, если три стороны одного треугольника соответственно равны трем сторонам другого треугольника. Два треугольника конгруэнтны, если две стороны и один треугольник между ними соответственно конгруэнтны с двумя сторонами и угол между ними в другом треугольнике.
Два треугольника конгруэнтны, если боковые и два угла, лежащие рядом с ним в одном треугольнике, соответственно конгруэнтны стороне и углы, лежащие на этой стороне во втором треугольнике. Продемонстрируйте, что два треугольника, обозначенные по диагонали в прямоугольнике, являются конгруэнтными.

Инструкция
Если известна величина угла (α), который составляет диагональ прямоугольника
с одной из его сторон, а также длина (С) этой диагонали, то для вычисления площади можно задействовать определения тригонометрических функций в прямоугольном треугольнике . Прямоугольный треугольник здесь образуют две стороны четырехугольника и его диагональ. Из определения косинуса вытекает, что длина одной из сторон будет равна произведению длины диагонали на
Прямоугольник – плоская фигура, у которой стороны
попарно равны и параллельны. Диагонали прямоугольника
тоже одинаковые. Одна диагональ
делит исходную фигуру на два прямоугольных треугольника с острыми углами по сорок пять градусов. Исходя из этих данных можно легко найти стороны
прямоугольника
, зная только численное значение диагонали.
Инструкция
Для нахождения сторон прямоугольника
нужно рассмотреть один из тех самых прямоугольных треугольников. В нем гипотенуза является диагональ
ю прямоугольника
, а катеты – его сторонами. Перед непосредственным вычислением с числовыми значениями нужно найти уравнения в общем виде. Для каждой стороны
будет свое уравнение. Итак, для получения формул, в прямоугольном треугольнике обозначьте катеты латинскими буквами а и b, а гипотенузу – с.
Решение задачи заключается в определении синуса и теоремы Пифагора. Выберите любой из острых углов в треугольнике (они равны), с которым будете работать. Определите прилежащий к нему катет и, противолежащий от него, другой катет. Например, пусть, прилежащим к углу, будет катет b, а находящимся напротив – катет а.
стороны прямоугольника
, если известна диагональ
” class=”lightbx” data-lightbox=”article-image”>
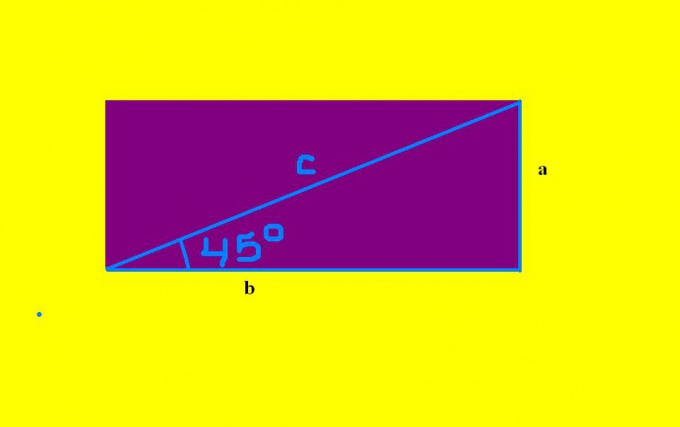
Далее, исходя из определения синуса, которое гласит, что синус угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе, составьте уравнение: sin 45 = а/с. В данном примере, по условию, известны: синус угла (sin 45 ~0,7) и гипотенуза с. Отсюда, получается уравнение 0,7=а/с, из которого а=0,7с. Осталось подставить численное значение с. Найденная сторона а будет равна параллельной стороне в прямоугольнике. Таким образом, известны две стороны
фигуры.
Загрузить PDF
Загрузить PDF
Найти длину неизвестной стороны прямоугольника можно несколькими способами, выбор которых зависит от того, какие параметры фигуры вам известны. Если дано значение площади или периметра, а также длина одной стороны прямоугольника (или соотношение между сторонами), можно с легкостью найти длину неизвестной стороны. Описанные методы позволят вам вычислить как ширину, так и длину прямоугольника.
-

1
-

2
В формулу подставьте данные значения площади и длины. Убедитесь, что подставляете числа вместо соответствующих им переменных.
- Например, найдите ширину прямоугольника, площадь которого равна 24 квадратных сантиметра, а длина 8 сантиметров. В этом случае формула запишется так:
- Например, найдите ширину прямоугольника, площадь которого равна 24 квадратных сантиметра, а длина 8 сантиметров. В этом случае формула запишется так:
-

3
Найдите
. Для этого разделите обе стороны уравнения на длину.
-

4
Запишите окончательный ответ. Не забудьте указать единицы измерения.
- Например, у прямоугольника, площадь которого равна 24 см2, а длина 8 см, ширина равна 3 см.
Реклама
-

1
-

2
В формулу подставьте данные значения периметра и длины. Убедитесь, что подставляете числа вместо соответствующих им переменных.
-

3
Найдите
. Для этого из обеих сторон уравнения вычтите длину, а затем обе стороны разделите на 2.
-

4
Запишите окончательный ответ. Не забудьте указать единицы измерения.
- Например, у прямоугольника, периметр которого равен 22 см, а длина 8 см, ширина равна 3 см.
Реклама
-

1
-

2
В формулу подставьте данные значения диагонали и длины. Убедитесь, что подставляете числа вместо соответствующих им переменных.
- Например, найдите ширину прямоугольника, диагональ которого равна 5 см, а длина 4 см. В этом случае формула запишется так:
- Например, найдите ширину прямоугольника, диагональ которого равна 5 см, а длина 4 см. В этом случае формула запишется так:
-

3
Обе стороны уравнения возведите в квадрат. Так вы избавитесь от квадратного корня и без труда обособите переменную
.
-

4
Обособьте
. Для этого из обеих сторон уравнения вычтите длину, возведенную в квадрат.
-

5
Найдите
. Для этого из обеих сторон уравнения извлеките квадратный корень.
-

6
Запишите окончательный ответ. Не забудьте указать единицы измерения.
- Например, у прямоугольника, диагональ которого равна 5 см, а длина 4 см, ширина равна 3 см.
Реклама
-

1
Запишите формулу для вычисления площади или периметра прямоугольника. Выбор конкретной формулы зависит от известных величин. Если дана площадь, запишите формулу для вычисления площади. Если дан периметр, запишите формулу для вычисления периметра.
-

2
Запишите уравнение, которое описывает зависимость длины от ширины. То есть с левой стороны уравнения оставьте переменную
.
- В задаче может быть указано, во сколько раз или на сколько единиц длина больше или меньше ширины.
- Например, длина больше ширины на 5 см. В этом случае уравнение примет следующий вид:
.
-

3
В формулу для вычисления площади (или периметра) вместо
подставьте записанное уравнение. В формуле останется одна переменная
, которую легко найти.
-

4
Упростите уравнение. Вид упрощенного уравнения зависит от соотношения между длиной и шириной и выбранной формулы (для вычисления площади или периметра).[7]
Упростите уравнение так, чтобы с легкостью найти значение переменной.
-

5
Найдите
. Способ вычисления ширины зависит от вида упрощенного уравнения. В процессе вычисления используйте основные правила алгебры и геометрии.
Реклама
Об этой статье
Эту страницу просматривали 113 530 раз.
Была ли эта статья полезной?
Как найти стороны прямоугольника, если известна диагональ
Прямоугольник – плоская фигура, у которой стороны попарно равны и параллельны. Диагонали прямоугольника тоже одинаковые. Одна диагональ делит исходную фигуру на два прямоугольных треугольника с острыми углами по сорок пять градусов. Исходя из этих данных можно легко найти стороны прямоугольника, зная только численное значение диагонали.

Инструкция
Для нахождения сторон прямоугольника нужно рассмотреть один из тех самых прямоугольных треугольников. В нем гипотенуза является диагональю прямоугольника, а катеты – его сторонами. Перед непосредственным вычислением с числовыми значениями нужно найти уравнения в общем виде. Для каждой стороны будет свое уравнение. Итак, для получения формул, в прямоугольном треугольнике обозначьте катеты латинскими буквами а и b, а гипотенузу – с.
Решение задачи заключается в определении синуса и теоремы Пифагора. Выберите любой из острых углов в треугольнике (они равны), с которым будете работать. Определите прилежащий к нему катет и, противолежащий от него, другой катет. Например, пусть, прилежащим к углу, будет катет b, а находящимся напротив – катет а.
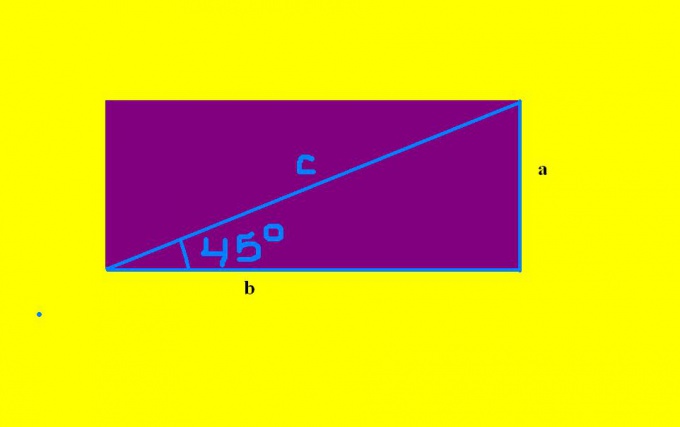
Далее, исходя из определения синуса, которое гласит, что синус угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе, составьте уравнение: sin 45 = а/с. В данном примере, по условию, известны: синус угла (sin 45 ~0,7) и гипотенуза с. Отсюда, получается уравнение 0,7=а/с, из которого а=0,7с. Осталось подставить численное значение с. Найденная сторона а будет равна параллельной стороне в прямоугольнике. Таким образом, известны две стороны фигуры.
Источники:
- Геометрия 7-9 классы. Погорелов. Просвещение 2010 год.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
» 2015 » Октябрь » 6 » Как найти ширину прямоугольника
|
06:14 Как найти ширину прямоугольника |
Как найти ширину прямоугольника4 методика:По площади и длинеПо периметру и длине По диагонали и длинеПо площади и разнице между длиной и шириной Эта статья расскажет вам, как найти ширину прямоугольника по известным величинам. Шаги
Метод 1 из 4: По площади и длине[1]
|
Категория: Вопросы и ответы | | Рейтинг: 3.0/3 |
Добавлять комментарии могут только зарегистрированные пользователи.
[
Регистрация
|
Вход
]






















