| Иррациональные числа ζ(3) — ρ — √2 — √3 — √5 — ln 2 — φ,Φ — ψ — α,δ — e — eπ и π |
|
| Система счисления | Оценка числа Φ |
| Десятичная | 1.6180339887498948482… |
| Двоичная | 1.1001111000110111011… |
| Шестнадцатеричная | 1.9E3779B97F4A7C15F39… |
| Шестидесятеричная | 1; 37 04 55 20 29 39 … |
| Рациональные приближения | 3/2; 5/3; 8/5; 13/8; 21/13; 34/21; 55/34; 89/55; …
|
| Непрерывная дробь | 
|
1,6180339887 4989484820 4586834365 6381177203 0917980576 2862135448 6227052604 6281890244 9707207204 1893911374 8475408807 5386891752 1266338622 2353693179 3180060766 7263544333 8908659593 9582905638 3226613199 2829026788 0675208766 8925017116 9620703222 1043216269 5486262963 1361443814 9758701220 3408058879 5445474924 6185695364 8644492410 4432077134 4947049565 8467885098 7433944221 2544877066 4780915884 6074998871 2400765217 0575179788 3416625624 9407589069 7040002812 1042762177 1117778053 1531714101 1704666599 1466979873 1761356006 7087480710 1317952368 9427521948 4353056783 0022878569 9782977834 7845878228 9110976250 0302696156 1700250464 3382437764 8610283831 2683303724 2926752631 1653392473 1671112115 8818638513 3162038400 5222165791 2866752946 5490681131 7159934323 5973494985 0904094762 1322298101 7261070596 1164562990 9816290555 2085247903 5240602017 2799747175 3427775927 7862561943 2082750513 1218156285 5122248093 9471234145 1702237358 0577278616 0086883829 5230459264 7878017889 9219902707 7690389532 1968198615 1437803149 9741106926 0886742962 2675756052 3172777520 3536139362
Первая тысяча знаков значения Φ[1].
Золотое сечение (золотая пропорция, иначе: деление в крайнем и среднем отношении, гармоническое деление) — отношение частей и целого, при котором отношения частей между собой и наибольшей части к целому равны. Такие отношения наблюдаются в природе, открыты в науке и соблюдаются в искусстве. На «золотых отрезках» основываются различные системы и способы пропорционирования в архитектуре. Соотношение двух величин 


Исторически в древнегреческой математике золотым сечением именовалось деление отрезка 


Число, равное отношению 


Из исходного равенства (например, принимая AB за 1, AC за неизвестную переменную y и BC за x, решая получившуюся систему уравнений x+y=1; x/y=1/x) нетрудно получить квадратное уравнение 


Обратное число, обозначаемое строчной буквой 
Отсюда следует, что
.
Число 
Для практических целей ограничиваются приблизительным значением 


Иллюстрация к определению
Золотое сечение имеет множество замечательных свойств (например, 

История[править | править код]
В дошедшей до нас античной литературе деление отрезка в крайнем и среднем отношении (ἄκρος καὶ μέσος λόγος) впервые встречается в «Началах» Евклида (ок. 300 лет до н. э.), где оно применяется для построения правильного пятиугольника[6].
Лука Пачоли, современник и друг Леонардо да Винчи, усматривал в этой пропорции «божественную суть», выражающую триединство Бога Отца, Сына и Святого Духа[7].
Неизвестно точно, кто и когда именно впервые ввёл в обращение термин «золотое сечение». Несмотря на то, что некоторые авторитетные авторы связывают появление этого термина с Леонардо да Винчи в XV веке[8] или относят появление этого термина к XVI веку[9], самое раннее употребление этого термина находится у Мартина Ома в 1835 году, а именно в примечании ко второму изданию его книги «Чистая элементарная математика»[10], в котором Ом пишет, что это сечение часто называют золотым сечением (нем. goldener Schnitt). Из текста этого примечания следует, что Ом не придумал этот термин сам[11][12], хотя некоторые авторы утверждают обратное[13]. Тем не менее, исходя из того, что в первом издании своей книги Ом уже не употреблял этот термин[14], Роджер Герц-Фишлер делает вывод о том, что этот термин, возможно, появился в первой четверти XIX века[15]. Марио Ливио считает, что он получил популярность в устной традиции около 1830 года.[16] В любом случае именно после Ома термин стал распространён в немецкой математической литературе[17].
Математические свойства[править | править код]
-
- Если угол между диагональю и меньшей стороной прямоугольника, относящейся к большей стороне как 1:2, поделить пополам, то по формуле тангенса половинного угла получится соотношение
- подходящими дробями которой служат отношения последовательных чисел Фибоначчи
. Таким образом,

Отрезание квадрата от прямоугольника, имеющего золотую пропорцию
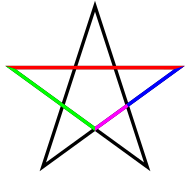
Золотое сечение в пятиконечной звезде

Построение золотого сечения
Другой способ построить отрезок, равный по длине числу золотого сечения
- Другой способ построить отрезок, равный по длине числу золотого сечения, — это начертить квадрат ABCD со стороной 1, после этого одну из сторон, например сторону AD, разделить точкой E пополам, так что AE = DE = 1/2, далее от точки B или C до точки E провести гипотенузу треугольника АВЕ или DCE. Согласно теореме Пифагора
. Затем провести дугу с центром в точке Е от точки В или точки С до прямой, где лежит сторона АD и точка пересечения где будет называться Н. Стороны BE, СЕ и ЕН равны как радиусы окружности. Так как АН = АЕ + ЕН, то отрезок АН длины
и будет результатом. Кроме того, поскольку DH = EH – ED, отрезок DH будет иметь длину
[18].
- где
— биномиальный коэффициент, тогда как
[источник не указан 2670 дней]
Золотое сечение в физике, геометрии, химии[править | править код]

Общее сопротивление этой бесконечной цепи равно 
Золотое число возникает в разных задачах, в том числе в физике. Например, бесконечная электрическая цепь, приведённая на рисунке, имеет общее сопротивление (между двумя левыми концами) 
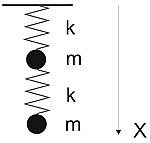
Отношение амплитуд колебаний и частот ~ Ф.
Существуют колебательные системы, физические характеристики которых (отношения частот, амплитуд и др.) пропорциональны золотому сечению. Самый простой пример — система из двух шариков, соединённых последовательно пружинами одинаковой жёсткости (см. рисунок).[20].
Более сложные примеры механических колебаний и их обобщений рассматриваются в этой[прояснить] же книге, в главе «Обобщения одной простой задачи по механике». В книге приведено много примеров проявления и применения золотого сечения в различных областях наук — небесной механике, физике, геофизике, биофизике, физической химии, биологии, Физиологии.
Золотое сечение тесно связано с симметрией пятого порядка, наиболее известными трёхмерными представителями которой являются додекаэдр и икосаэдр. Можно сказать, что всюду, где в структуре проявляются додекаэдр, икосаэдр или их производные, там в описании будет появляться и золотое сечение. Например, в пространственных группировках из Бора: В-12, В-50, В-78, В-84, В-90, …, В-1708, имеющих икосаэдрическую симметрию[21].
Молекула воды, у которой угол расхождения связей Н-О равен 104.70 , то есть близок к 108 градусам (угол в правильном пятиугольнике), может соединяться в плоские и трехмерные структуры с симметрией пятого порядка. Так в разреженной плазме был обнаружен Н+(Н20)21, который представляет собой ион Н30+, окруженный 20 молекулами воды, расположенными в вершинах додекаэдра[22]. В 80-х годах XX века были получены клатратные соединения, содержащие гексааквакомплекс кальция, окруженный 20 молекулами воды, расположенными в вершинах додекаэдра[23]. Есть и клатратные модели воды, в которых обыкновенная вода отчасти состоит из молекул воды, соединённых в структуры с симметрией пятого порядка. Такие структуры могут состоять из 20, 57, 912 молекул воды[24].
Золотое сечение и гармония в искусстве[править | править код]
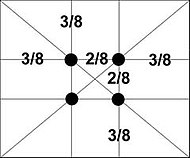
Иллюстрация композиционного значения золотого сечения.
Некоторые из утверждений в доказательство гипотезы знания древними правила золотого сечения:
- Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют о том, что при их создании египетские мастера пользовались соотношениями золотого сечения. Меры длины Древнего Египта также были созданы с помощью золотого сечения. Пример: π —
² = 0,5235 м (Локоть царский). Атур обычный = 5,235 км.
- По мнению Ле Корбюзье, в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют золотому сечению. В фасаде древнегреческого храма Парфенона также присутствуют золотые пропорции. В циркуле из древнеримского города Помпеи (музей в Неаполе) также заложены пропорции золотого деления, и т. д.

Примеры сознательного использования[править | править код]
Начиная с Леонардо да Винчи, многие художники сознательно использовали пропорции «золотого сечения». Российский зодчий И. В. Жолтовский использовал золотое сечение в своих проектах[25].
Иоганн Себастьян Бах в своей трёхголосной инвенции E-dur № 6 BWV 792 использовал двухчастную форму, в которой соотношение размеров частей соответствует пропорциям золотого сечения. 1 часть — 17 тактов, 2 часть — 24 такта (небольшие несоответствия выравниваются за счёт ферматы в 34 такте)[26].
Современными примерами применения золотого сечения может служить мозаика Пенроуза и пропорции государственного флага Того.
Золотое сечение в биологии и медицине[править | править код]

Золотое сечение в природе
Живые системы также обладают свойствами, характерными для «золотого сечения». Например: пропорции тел, спиральные структуры или параметры биоритмов[27][неавторитетный источник?] и др.
См. также[править | править код]
- Божественная пропорция
- Золотая спираль
- Золотой прямоугольник
- Пифагорейский пентакл
- Пропорционирование
- Фибоначчиева система счисления
- Правило третей
- Метод золотого сечения
- Сверхзолотое сечение
- Пластическое число
- Золотой угол
- Канон (искусство)
- Модулор
- Числа Фибоначчи
- Обобщение чисел Фибоначчи
- Обобщённое золотое сечение
Примечания[править | править код]
- ↑ Взята из примера результата компьютерного расчета (1996 года) с гораздо большим числом знаков, чем 1000 Golden ratio 1000 digits Архивная копия от 6 марта 2015 на Wayback Machine
- ↑ 1 2 Савин А. Число Фидия – золотое сечение (рус.) // “Квант” : Научно-популярный физико-математический журнал (издается с января 1970 года). — 1997. — № 6. Архивировано 4 марта 2016 года.
- ↑ Радзюкевич А. В. Красивая сказка о «золотом сечении». Дата обращения: 22 марта 2012. Архивировано 29 декабря 2011 года.
- ↑ Mario Livio, The Golden Ratio: The Story of Phi, The World’s Most Astonishing Number
- ↑ Devlin’s Angle, The Myth That Will Not Go Away
- ↑ Livio, Mario. The Golden Ratio: The Story of Phi, the World’s Most Astonishing Number. — First trade paperback. — New York City : Broadway Books, 2003. — ISBN 978-0-7679-0816-0. Архивная копия от 31 марта 2019 на Wayback Machine
- ↑ В. Лаврус, Золотое сечение. Дата обращения: 18 июля 2004. Архивировано 20 июня 2004 года.
- ↑ François Lasserre. The birth of mathematics in the age of Plato. — American Research Council, 1964-01-01. — 200 с. — P. 76. Архивировано 18 июня 2016 года.
- ↑ Boyer, Carl B. A History of Mathematics (неопр.). — Second Edition. — John Wiley & Sons, Inc., 1991. — С. 50. — ISBN 0-471-54397-7.
- ↑ Martin Ohm. Die reine Elementar-Mathematik. — 2-е изд. — Jonas Verlags-buchhandlung, 1835. — С. 194. — 454 с. Архивировано 23 июля 2016 года.
- ↑ Herz-Fischler, 2013, p. 168.
- ↑ Livio, 2008, p. 6—7.
- ↑ Василенко С. Л. Знак-символ золотого сечения // Академия Тринитаризма. — М., 05.02.2011. — № Эл № 77—6567, публ. 16335. Архивировано 26 ноября 2015 года.
- ↑ Martin Ohm. Die reine Elementar-Mathematik. — 1-е изд.. — Berlin, 1826. — 492 с. — P. 188. Архивировано 30 мая 2016 года.
- ↑ Herz-Fischler, 2013, p. 169.
- ↑ Livio, 2008, p. 7.
- ↑ Herz-Fischler, 2013, p. 169—170.
- ↑ Тони Крилли. Математика: 50 идей, о которых нужно знать = 50 Mathematical Ideas you really need to know. — Phantom Press. — 209 с. — ISBN 9785864716700. Архивировано 18 июня 2016 года.
- ↑ Системы счисления. Дата обращения: 13 ноября 2014. Архивировано 28 ноября 2014 года.
- ↑ Ковалев А.Н. В поисках пятого порядка. — 2017. — 374 с. — ISBN 978-5-4485-3753-0.
- ↑ Современная Кристаллография / под ред. Вайнштейна Б. К.. — Т.2. — М.: Мир, 1979.
- ↑ Holland P. M. Casteiman A. W. A model for the formation and stabilization of chorqed water cluthrates // J. Chem. Phys.. — 1980. — Т. 72, № 1(11). — С. 5984.
- ↑ Электромагнитные поля в биосфере. — Сборник трудов конференции, Т.2. — М., 1984. — С. 22.
- ↑ Зенин С.В. Структурированное состояние воды как основа управления поведением и безопасностью живых систем. — Диссертация докт. биол. наук. — М., 1999.
- ↑ Золотой запас зодчества Архивная копия от 29 января 2009 на Wayback Machine
- ↑ Бах И.С. 15 двухголосных инвенций и 15 трехголосных симфоний. — М.: Музгиз, 1961. — С. 46. — 70 с.
- ↑ Цветков, В. Д. Сердце, золотое сечение и симметрия. — Пущино: ПНЦ РАН, 1997. — 170 с. Дата обращения: 19 февраля 2015. Архивировано 27 сентября 2015 года.
Литература[править | править код]
- на русском языке
- Аракелян Г. Б. Математика и история золотого сечения. — М.: Логос, 2014, 404 с. — ISBN 978-5-98704-663-0.
- Бендукидзе А. Д. Золотое сечение Архивная копия от 11 октября 2004 на Wayback Machine «Квант» № 8, 1973
- Васютинский Н. А. Золотая пропорция. — М.: Молодая гвардия, 1990. — 238[2]c. — (Эврика).
- Власов В. Г. Золотое сечение, или Божественная пропорция // Власов В. Г. Новый энциклопедический словарь изобразительного искусства: В 10 т. — Т.3. — СПб.: Азбука-Классика, 2005. — С.725-732.
- Власов В. Г. Приемы гармонизации пространства в классической архитектуре // Власов В. Г. Искусство России в пространстве Евразии. — Т.3. Классическое искусствознание и «русский мир». — СПб.: Дмитрий Буланин, 2012. — С.156-192.
- Мазель Л. А. Опыт исследования золотого сечения в музыкальных построениях в свете общего анализа форм // Музыкальное образование. — 1930. — № 2. — С. 24-33.
- Сабанеев Л. Л. Этюды Шопена в освещении закона золотого сечения. Опыт позитивного обоснования законов формы // Искусство. — 1925. — № 2. — С. 132—145; 1927. — № 2-3. — С. 32-56.
- Шевелев И.Ш., Марутаев М.А., Шмелев И.Л. Золотое сечение. Три взгляда на природу гармонии. — М.: Стройиздат, 1990. — 343 с. — ISBN 5-274-00197-1.
- Шевелев И.Ш. Геометрическая гармония. Опыт исследования пропорциональности в архитектуре. — Кострома, 1963. — 107 с.
- Шмигевский Н. В. Формула совершенства // Страна знаний. — 2010. — № 4. — С.2-7.
- на других языках
- Mario Livio. The Golden Ratio: The Story of PHI, the World’s Most Astonishing Number. — Crown/Archetype, 2008. — 303 с. — ISBN 9780307485526. Архивная копия от 31 марта 2019 на Wayback Machine Русский перевод в
- Марио Ливио. φ – Число Бога. Золотое сечение – формула мироздания. — Litres, 2015-04-17. — 481 с. — ISBN 9785457762732. Архивная копия от 24 июня 2016 на Wayback Machine
- Roger Herz-Fischler. A Mathematical History of the Golden Number. — Courier Corporation, 2013. — 228 с. — ISBN 9780486152325. Архивная копия от 2 июля 2016 на Wayback Machine
Ссылки[править | править код]
- В. С. Белнин, «Владел ли Платон кодом золотой пропорции? Анализ мифа»
- А. В. Радзюкевич, К вопросу о научном изучении пропорций в архитектуре и искусстве Архивная копия от 3 апреля 2015 на Wayback Machine.
- А. В. Радзюкевич, Критический анализ Адольфа Цейзинга — основоположника гипотезы «золотого сечения». Архивная копия от 19 декабря 2014 на Wayback Machine
- Статья о золотом сечении в изобразительном искусстве, Золотое сечение в изобразительном искусстве
- J. J. O’Connor, E. F. Robertson. Golden ratio. MacTutor History of Mathematics archive. School of Mathematics and Statistics, University of St Andrews, Scotland. Дата обращения: 13 ноября 2015. Архивировано 25 июля 2015 года.
- Функция Фибоначчи Архивная копия от 30 октября 2020 на Wayback Machine в Wolfram alpha
Что такое золотое сечение и правда ли оно повсюду
Спойлер: это лишь красивая математическая легенда.

Что такое золотое сечение
Это соотношение двух неравных чисел, при котором большее так же относится к меньшему, как сумма этих чисел к большему. Золотое сечение равно примерно 1,618, или 1,62, если округлить, и обозначается греческой буквой φ, «фи» — от имени древнегреческого скульптора Фидия. Считается, что он использовал такие пропорции при оформлении Парфенона.
Наиболее известные графические представления золотого сечения — это прямоугольник с соотношением сторон примерно 62:48 и построенная в нём спираль.
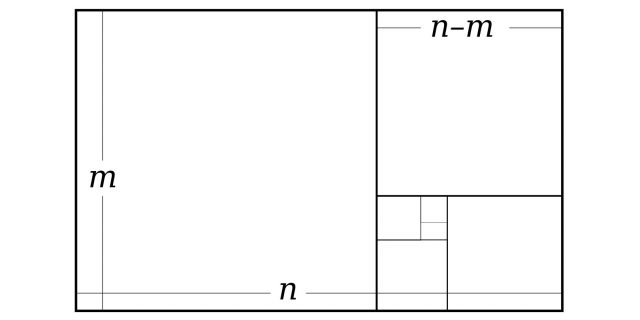
1 / 0
«Золотой прямоугольник» можно разделить на такие же, только меньшего размера. Изображение: Dicklyon / Wikimedia Commons
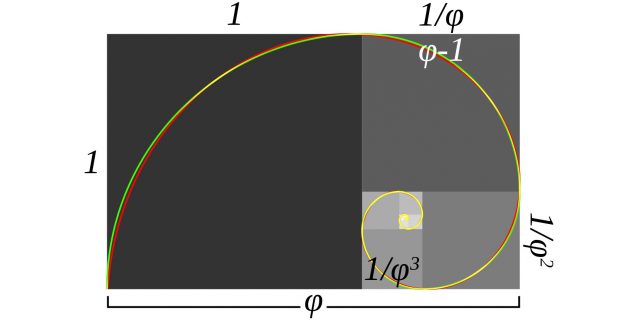
2 / 0
«Золотая спираль» (красная), вписанная в «золотой прямоугольник». Изображение: Silverhammermba & Jahobr / Wikimedia Commons
Золотое сечение тесно связано с числами Фибоначчи. Это ряд чисел, каждое из которых равняется сумме двух предыдущих: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 и так далее. Чем дальше продолжается этот ряд, тем ближе соотношение соседних чисел в нём к 1,618. Например, 3/2=1,5; 8/5=1,6, а 34/21= 1,619.
Почему золотое сечение так популярно
Впервые им заинтересовались ещё древнегреческие математики Пифагор и Евклид. Они считали, что на числах построено всё мироздание и с их помощью можно объяснить любой феномен. Неудивительно, что элегантное соотношение так заинтересовало античных мыслителей.
Вслед за ними золотым сечением увлеклись многие выдающиеся учёные и деятели искусства. Например, Леонардо да Винчи, Альбрехт Дюрер, Иоганн Кеплер, Ле Корбюзье, Сальвадор Дали и Ричард Пенроуз.
Его считают «божественной пропорцией»
Название «золотое сечение» придумал немецкий математик XIX века Мартин Ом. До него это соотношение именовали «божественной пропорцией».
Из‑за приписываемых характеристик золотое сечение старались применять как можно чаще. Так, во времена Возрождения это число считалось идеальным способом для выбора размера. «Золотой прямоугольник», например, нередко использовали при создании книг и картин. А линию пояса называли границей золотого сечения человеческого тела.
Некоторые и поныне считают эту пропорцию секретом привлекательности и примером универсальной гармонии, приятной человеческому глазу. Например, о золотом сечении любят говорить пластические хирурги. А ещё это число популярно как никакое другое в математике.
Его можно встретить в природе
Числа Фибоначчи и спирали, подобные золотому сечению, часто обнаруживаются в природе. Например, в количестве лепестков у цветов или форме растений.
Его обнаруживают в произведениях архитектуры и искусства
Например, «божественные пропорции» находят в Парфеноне и египетских пирамидах. Также широко распространено заблуждение, что «Мона Лиза» написана в соответствии с числом φ.
Почему универсальность золотого сечения — миф
Однако при тщательном изучении становится понятно, что эта пропорция не так уж всеобъемлюща.
Божественность золотого сечения преувеличивается
Золотому сечению придают больше значения, чем есть в действительности. Красивые узоры и налёт таинственности сделали из обычного геометрического соотношения математический миф, который, к примеру, очень любят нумерологи.
Чаще всего вещи причисляют к золотому сечению с большими допущениями. Ни о какой точности и математической универсальности в таком случае говорить не приходится. Поэтому при желании можно обнаружить «божественные пропорции» где угодно.
В природе золотое сечение не так уж распространено
Его находят далеко не везде. Например, у маков всегда четыре лепестка, а в ряд Фибоначчи четвёрка не входит. Также нередко встречается четырёхлистный клевер. Раковины морских моллюсков похожи на спираль золотого сечения, но всё-таки другие. У них больше витков, и расстояние между ними меньше. Ни у одного моллюска коэффициент скручивания раковины и близко не равен 1,62. Это видно даже невооружённым глазом:

1 / 0
Спираль морского моллюска. Изображение: Florian Elias Rieser / Wikimedia Commons
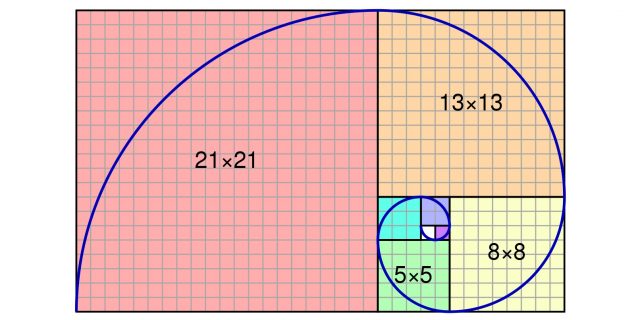
2 / 0
Спираль Фибоначчи, близкая к золотому сечению. Изображение: Jahobr / Wikimedia Commons
В человеческом теле же столько точек, от которых можно производить измерение, что при желании реально найти золотое сечение где угодно. Вот только с большой вероятностью у разных людей «божественную пропорцию» придётся искать в разных местах, так как мы можем сильно отличаться друг от друга.
В искусстве оно тоже встречается не так уж часто
Изучение 565 картин выдающихся художников показало, что в среднем соотношение сторон в работах составляет 1,34. Это явно не дотягивает до золотого сечения. Учёные не находят его даже в произведениях Леонардо да Винчи.
Археологические исследования не подтверждают и того, что древние греки могли использовать золотое сечение при постройке Парфенона. Из более чем 100 памятников древнегреческой архитектуры это число нашлось в пропорциях только четырёх объектов: башни, алтаря, гробницы и надгробия. Не могли пользоваться золотым сечением и древние египтяне, не обладавшие достаточным уровнем технологий, чтобы точно высчитывать пропорции.
Кому золотое сечение может быть полезно на самом деле
Современная математика использует золотое сечение и числа Фибоначчи при описании фракталов — фигур, которые проявляют самоподобие.
Знание о числе φ играет важную роль в изучении хаоса и изменяющихся (динамических) систем. Оно помогает понять, как природа развивается и самоорганизуется.
Также числа Фибоначчи полезны при решении некоторых сложных задач. Например, с помощью этих чисел советский математик Юрий Матиясевич доказал, что не существует универсального алгоритма решения уравнений с как минимум двумя неизвестными.
Читайте также 
- Продолжите последовательность! 10 мини-задач для разминки мозга
- Как округлять числа
- Интересные математические факты для тех, кто хочет больше узнать о мире вокруг
- Гимнастика для ума: 10 увлекательных задач с числами
- 10 увлекательных задач от советского математика
Что это? Золотое сечение – это математическая формула, соотношение двух неравных чисел. Его еще называют божественной пропорцией. Правило третей, золотая спираль – всё это визуальное отображения этого универсального правила.
Где используется? Золотое сечение применимо везде, где есть место графике, рисунку, фотографии. Сфера дизайна – не исключение. Конечно, это не единственное правило гармонии, но, пожалуй, самое известное.
В статье рассказывается:
- Что такое золотое сечение
- История золотого сечения
- Золотое сечение Фибоначчи
- Золотое сечение в природе
- Золотое сечение в фотографии
- Золотое сечение в дизайне
-
Пройди тест и узнай, какая сфера тебе подходит:
айти, дизайн или маркетинг.Бесплатно от Geekbrains
Что такое золотое сечение
Это отношение двух разных по величине чисел, когда большее из них относится к меньшему так же, как и общая их сумма относится к большему. Соотношение золотого сечения равняется около 1,618. Его обозначают греческой литерой Ф (читается как «фи») в честь древнегреческого скульптора Фидия, который применял эти пропорции при создании храма Парфенон.
Одним из популярных способов представления золотого сечения является прямоугольник с соотношением сторон 62 на 48 и построенной внутри спиралью.

История золотого сечения
Согласно истории, данное понятие для научного использования ввел Пифагор, философ и математик Древней Греции. Предполагается, что ученый позаимствовал знание у жителей Египта и Вавилонии.
Если посмотреть на соотношение сторон пирамид, храмов и предметов домашнего обихода у древних египтян, а также на украшения из саркофага царя Тутанхамона, то очевидно, что все они создавались по принципу золотого сечения.
Архитектор из Франции Ле Корбюзье заметил, что рельеф храма египетского правителя Сети I, как и в рельефе изображения царя Рамзеса, тоже создавались по этому правилу. Соотношения золотого деления были обнаружены и в рельефе гробницы, на котором изображен высокопоставленный чиновник Хесира.
Скачать
файл
Жители Древней Греции хорошо владели геометрией. Арифметике, например, они учились по геометрическим фигурам уже в детстве. А квадрат Пифагора и его диагональ служили основой для создания динамических прямоугольников.
Сам термин «золотое сечение» впервые ввел в обиход математик из Германской империи Мартин Ом в 19 веке. До того времени правило имело название «божественная пропорция».
Из-за уникальных свойств она пользовалась большой популярностью. Например, в эпоху Возрождения число 1,618 было идеальным при выборе размера. Его часто применяли для создания картин и книг. А линия талии в то время считалась границей золотого сечения в теле человека.
Многие люди и сегодня уверены, что соблюдение данного правила считается залогом красоты и внешней гармонии. Эту тему активно обсуждают пластические хирурги.
Золотое сечение Фибоначчи
В конце 12 века математик из Италии Леонардо Пизанский, известный по прозвищу Фибоначчи, открыл последовательность чисел, связанных с золотой пропорцией. Суть в том, что если взять любые 2 числа из ряда итальянского математика, то соотношение между ними почти такое же, как на примерах золотого сечения. Особенность последовательности Фибоначчи в том, что каждое новое число всегда равняется сумме 2-х предыдущих. Пример: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и т. д.
По мере увеличения ряда, отношения между числами становится все ближе к 1,618. Разделив, к примеру, 8 на 5, мы получим около 1,6. А соотношение 34 на 21 уже дает 1,619, если округлить. Каждое число ряда является логичным в последовательности Фибоначчи.

Читайте также
Такие соотношения из-за приближения к показателю золотого деления можно использовать при построении золотого прямоугольника. Эта фигура считается одной из самых гармоничных в геометрии, что позволяет применять пропорции Пифагора в любом виде изобразительного искусства.
Золотой прямоугольник тесно связан с золотой спиралью, которая строится методом размещения смежных между собой квадратов по алгоритму Фибоначчи.
Золотое сечение в природе
Пропорции золотого сечения можно наблюдать во всех природных и научных проявлениях. В представленном списке мы рассмотрим наиболее удивительные случаи.
- Лепестки у цветов. Нередки случаи, когда их количество соответствует числовому ряду «Ф». По мнению Дарвина, все лепестки растений располагаются так, чтобы получать как можно больше солнечного света и остальных необходимых для жизни ресурсов.
- Головки у семян. Во многих случаях семена цветов начинают расти посередине головки семени и появляются снаружи, заполняя собой пространство. В качестве примера можно привести семена подсолнуха.
- Шишки у сосен. Семена, находящиеся в их семенных коробочках, произрастают вверх противоположно друг другу по спирали. Расстояние между ними обычно совпадает с соотношениями чисел из последовательности Фибоначчи.
- Ветки у деревьев. На примере их формирования и расщепления также можно заметить правило золотого ряда. То же самое относится и к развитию корневых систем у растений и водорослей.
- Раковины. Большинство из них демонстрируют нам правило золотого сечения. Например, это можно сказать об улитках и наутилусах.

- Спиральные галактики. Млечный Путь содержит в себе несколько рукавов, представленных в виде изогональных спиралей с шагом около 12 градусов. Их форма соответствует форме золотой спирали, при том над каждой такой галактикой можно начертить золотой прямоугольник.
- Ураганы. В большинстве случаев, изнутри они устроены согласно последовательности ряда «фи».
- Пальцы на руках у людей. Все участки пальцев от начала основания и до запястья увеличивается в соотношении по Фибоначчи.
- Тела людей и животных. Расстояние у людей от пупка до пола, а также от темени и до пупка — это яркий пример закона золотого сечения. Помимо человека такую пропорцию можно наблюдать и у других организмов (например, у дельфинов и пчел).
- Молекулы ДНК. Все они содержат соотношение 34 на 21 ангстрем в каждом полном спиральном цикле. А вы уже знаете, что эти цифры — часть ряда Фибоначчи.
Топ-30 самых востребованных и высокооплачиваемых профессий 2023
Поможет разобраться в актуальной ситуации на рынке труда

Подборка 50+ ресурсов об IT-сфере
Только лучшие телеграм-каналы, каналы Youtube, подкасты, форумы и многое другое для того, чтобы узнавать новое про IT
ТОП 50+ сервисов и приложений от Geekbrains
Безопасные и надежные программы для работы в наши дни
Уже скачали 20827
Как мы видим, примеров, где можно увидеть пропорции и соотношения по принципу золотого правила, довольно много. Помимо случаев, описанных выше, 1,618 постоянно встречается в точных науках, биологии и других областях жизни. Поэтому свое альтернативное название — божественное сечение, правило полностью оправдывает. Ведь материальный мир словно был создан по этому закону.
Золотое сечение в фотографии
Гармоническая пропорция напрямую связана с правилом третей — другой неотъемлемой схемой для работы с визуалом. По сути, оно продолжает золотое сечение так же, как, например, фотография рождается из художественного творчества.
Основное различие заключается в соотношении сторон. Так, в принципе третей кадр разделяется на 3 одинаковые части, а в божественной пропорции он делится на 1:0.618:1.
Отсюда следует, что правило третей можно назвать более простой версией золотого сечения, но полностью рабочей.
Например, сегодня большинство камер, в том числе и в смартфонах, имеет разлинованную сетку третей, что позволяет пользователям гармонично выстраивать композицию из фото и видео.
Чем следует руководствоваться при съемке?
- Точки пересечения. Благодаря размещению нужного объекта по линиям, сделать снимок будет намного удобнее.
- Диагональная композиция. Линию можно прочертить самостоятельно из верхнего угла кадра в нижний, а можно использовать объекты, находящиеся в этой последовательности, которые формируют эту линию. Наличие разных диагоналей позволяет получить динамичный кадр. Восходящая, например, из правого нижнего угла в левый верхний придаст фотографии веселое настроение, а нисходящая — грустное.
- Пропорции. Чаще всего это относится к взаимосвязи объектов на нескольких планах снимка. Это тоже вариант золотого сечения, только представленный в соотношении объектов. Например, на заднем плане к большему объекту на переднем плане (либо наоборот).
- Линия горизонта. Когда вы делаете снимок на природе либо в городской инфраструктуре, нужно расположить горизонтальную линию кадра на одной из горизонтальных линий третей. То же самое относится и к общему плану фотографии/видео. Это даст более качественный результат.
- Правило «воздуха». Не забывайте про свободные участки между объектами. Если вы делаете фотографию человека, то оставьте немного пространства от его головы до границы кадра. А в ситуации, когда он смотрит налево, разместите человека по правым точкам пересечения линий (верно и обратное).
Золотое сечение в дизайне
Божественная пропорция делает современный дизайн более упорядоченным. Легкий и быстрый способ использования этого — умножить размер одного элемента на 1,618. Результат покажет, каким должен быть размер следующего объекта.
Только до 18.05
Скачай подборку тестов, чтобы определить свои самые конкурентные скиллы
Список документов:
 Тест на определение компетенций
Тест на определение компетенций
 Чек-лист «Как избежать обмана при трудоустройстве»
Чек-лист «Как избежать обмана при трудоустройстве»
 Инструкция по выходу из выгорания
Инструкция по выходу из выгорания
Чтобы получить файл, укажите e-mail:
Подтвердите, что вы не робот,
указав номер телефона:

Уже скачали 7503
Применение формулы золотого сечения в типографике
Определяющими факторами в данной области являются 3 составляющие: размер шрифта, ширина линии и высота строки. Их необходимо подбирать в правильных пропорциях.
Увеличивая и уменьшая шрифт, а также ширину текста, можно определить, какую высоту следует задать буквам. Установлено, что оптимальным для удобства читателей количеством является 70-80 символов на строку. Когда длина текста превышает этот показатель, его читабельность сильно снижается.
Для примера возьмем текст из 3 строк и определим в нем 3 части: «А», «Б» и «В». Допустим, строка «В» содержит меньше ценной информации, чем «А» и «Б». В связи с этим, текст внутри строки «В» должен иметь шрифт размером 10. Чтобы установить размер контента на строке «Б» (второй по значимости контента), надо умножить 10 на 1,618.
В разработке логотипов
Большинство популярных брендов, например, «Твиттер», «Эппл» и «Пепси», применяют знания божественного сечения, когда создают фирменный логотип.
Поэтому вы тоже можете пользоваться правилом чисел «Ф» при создании сетки. Полученный результат станет вашей опорой в разработке графического рисунка.
Золотое сечение в архитектуре
Зодчие прошлого применяли принцип божественного деления при создании памятников. Мавзолей-мечеть Тадж-Махал, например, относится к одному из 7 чудес света. Когда его возводили, мастера пользовались правилом золотого сечения.

Применение этого знания в современной архитектуре дает возможность добиться баланса между шириной и высотой сооружения. Популярным методом построить гармоничное здание является использование свойств золотого прямоугольника.
Стоит добавить, что золотое сечение дает возможность творить разнообразные формы. При их создании нет необходимости строго следовать прямоугольной структуре. Золотое деление позволяет дизайнерам применять полученные формы как основу для работы.
Разработка проектов и формирование макетов
Чтобы сделать макеты качественными, нужно учесть 2 главные составляющие: отдельные визуальные элементы и как они будут связаны между собой.
Есть много способов формирования макетов. Например — расположение «Z». Оно дает увидеть путь, по которому проходит посетитель на веб странице, а также схему того, как он смотрит на элементы.
Еще одно востребованное правило компоновки — это применение золотой спирали. Она более эффективно, если в дизайне достаточно много элементов, различающихся между собой, но предназначенные для расположения на одном макете. Благодаря использованию правил сечения внимание посетителей ненавязчиво, но эффективно притягивается к середине спирали, в которой можно расположить главный элемент контента.

Читайте также
Некоторые считают, что золотое сечение в большей или меньшей степени присутствует в каждом успешном дизайне. Рассказать о востребованной концепции бывает полезным в общении с заказчиком или когда нужно показать свой проект публично. Действительно ли «божественная пропорция» очень эффективна или это мнение преувеличено? Обсуждение данного вопроса в творческой сфере продолжается и сегодня.
Число Ф (фи), которое называют золотым сечением или серединой, является одним из самых загадочных терминов в математике и физике. Интересно, что оно часто встречается в повседневной жизни, хотя многие об этом никогда не задумывались. Даже люди, не знакомые с правилом золотого сечения, видят его, сами того не понимая. Проводились эксперименты: испытуемым показывали случайные лица и просили назвать наиболее привлекательные. Таковыми оказывались лица, в которых находили золотые соотношения между различными величинами – шириной лица, глаз, линии бровей, носа. Таким образом, инстинктивно человек видит приближенное к пропорциям, которые считаются идеальными.
Содержание:
- 1 Что такое золотое сечение?
- 2 История золотого сечения
- 3 «Золотые» фигуры
- 4 Золотое сечение в изобразительном искусстве
- 5 Примеры золотого сечения в жизни и в природе
Что такое золотое сечение?
Это пропорция, полученная делением в крайнем и среднем отношении. Также это называют гармоническим делением. Как вычисляется золотая середина? В выражении математическим языком эта величина представляет собой соотношение двух величин a и b, где известно, что а>b, и имеет место такое равенство: a/b=(a+b)/a. Представив, что a и b – это части одного отрезка, можно сказать: отношение меньшей части к большей равно отношению большей части к целому. Золотое сечение обозначают 21-й буквой греческого алфавита – Ф (произносится как «фи»).
Данное число бесконечно, как и Пи, показывающее отношение длины окружности к диаметру. Выглядит оно так: 1.6180339887498948420… Соответственно, округляют Ф до 1,618.
История золотого сечения
У этой величины несколько названий. Среди них – божественная пропорция и асимметричная симметрия. Считается, что в науку метод золотого деления внес Пифагор в VI веке до нашей эры. В свою очередь он узнал об этом у египтян и вавилонян. Ведь то, что они использовали соотношения золотого деления доказывают пропорции пирамид, храмов, барельефов, предметов быта и украшений.
Встречается данное правило и в другой древней архитектуре. Например, пирамида Гизы имеет высоту 146,6 метров, а каждая сторона основания достигает 230,5 метров. Если рассчитать отношение длины стороны к высоте, получаем 1,5717, а это совсем рядом со значением Ф. Греческий скульптор и математик Фидий, живший в V веке до нашей эры с применением правила золотого деления создавал скульптуры для Парфенона. Универсальным связующим звеном математических отношений назвал золотое сечение Платон. А Евклид еще в IV веке до нашей эры увидел золотое сечение в пентаграмме.
С данным понятием непосредственно связана последовательность Фибоначчи. Известный математик создал последовательный ряд чисел, и если взять любые два очередных числа, то их отношение будет очень близко к Ф. При этом по мере возрастания чисел, соотношение всё больше приближается к 1,618. К примеру, если взять 3 и 5, то соотношение равно 1,666, а если 13 и 21, то получается уже 1,625. Равное значению Ф дает отношение 144 и 233.
«Золотые» фигуры
Принцип золотого сечения используется для построения геометрических фигур. И считается, что полученные таким образом фигуры, выглядят наиболее изящными. Это подтверждают многократно проведенные эксперименты. Внимание испытуемых больше привлекают именно такие фигуры.

Самым простым примером является прямоугольник, при вычислении отношения сторон которого получаем значение Ф. Еще один замечательный пример – правильный пятиугольник. Все его диагонали делят друг друга на отрезки, связанные золотой пропорцией, а каждый конец – это золотой треугольник. При вершине такого треугольника образуется угол в 36 градусов, а основание делит боковую сторону в пропорции золотого сечения. Внутри пятиугольника строится пентаграмма.
Древнегреческий ученый Архимед, первым отметил, что если от золотого прямоугольника последовательно отсекать квадраты, соединяя противоположные точки четвертью окружности, получается изящная спираль.
Золотое сечение в изобразительном искусстве
В эпоху Возрождения при создании картин и скульптур великие мастера применяли золотое сечение, чтобы достичь баланс красоты. Наиболее яркими примерами являются творения Леонардо да Винчи. С помощью этого правила художник определял пропорции в работе «Тайная вечеря». Это видно при исследовании размеров стола, стен, элементов интерьера. Также божественная пропорция прослеживается в картинах «Мона Лиза» и «Витрувианский Человек». Такие великие художники, как Микеланджело, Рафаэль, Рембрандт, Сальвадор Дали и другие, использовали золотое сечение при создании своих шедевров.
Примеры золотого сечения в жизни и в природе
Ежедневно мы можем наблюдать идеальные пропорции:
- Грудная и брюшная части тела бабочки соотносятся в золотой пропорции. А при сложенных крыльях это прекрасное создание представляет собой правильный треугольник с равными сторонами.
- У стрекозы длины хвоста и корпуса относятся так же, как общая длина тела к хвосту.
- В пропорциях тела ящерицы также прослеживается данный принцип.
- Большинство яиц птиц можно вписать в золотой прямоугольник.
- Последовательность Фибоначчи видна в развитии растений, в расположении чешуек в шишках, зерен в подсолнухах.
- Спирально растет бараний рог, плетет паутину паук.
- Интересно, что если напугать стадо северных оленей, то животные будут разбегаться по спирали.
- В форме двойной спирали представлена молекула ДНК.
- Цветки разных растений, а также морские звезды имеют форму правильного пятиугольника.
Как видно, примеров с правильными пропорциями в природе и повседневной жизни предостаточно. Не даром золотое сечение называют божественной пропорцией. Вероятно, именно этим правилом руководствовался создатель в процессе заполнения Вселенной живыми и неживыми объектами. То, что соответствует этому правилу, кажется нам наиболее привлекательным.
В мире много интересных вещей, изучение нового делает нас умнее, способствует развитию мозга и мышления. Советуем вам обязательно находить время на познание нового. А чтобы было легче усваивать и запоминать большие объемы информации, рекомендуем тренажеры Викиум. Регулярно используя их для тренировок мозга, вы сможете улучшить память, внимательность, логику и аналитические способности.
Довольно часто говорят, что в математике есть своя красота, но уже к середине V века до н. э. или даже значительно раньше стало известно, что в красоте большое количество математики. Золотое соотношение — это число, у которого, по всей видимости, больше имен, чем у любого другого. Его именуют золотым сечением, божественной пропорцией либо попросту — фи (φ).
Это число обозначает очень приятную — в большинстве случаев — пропорцию, появляющуюся при делении чего-либо на две неравные части. Значительно чаще золотое соотношение возможно встретить при взоре на монументы искусства и архитектуры любого исторического периода. Свое имя число фи взяло в честь греческого архитектора и скульптора Фидия, который, по утверждению некоторых исследователей, деятельно применял данный принцип для украшения самого своего известного творения — Парфенона, возведенного в 440 г. до н. э.
Старейшее сохранившееся до наших дней описание принципа золотого соотношения было сделано Евклидом около 300 г. до н. э. в его труде «Начала». Но самое восхитительное в числе фи — не его настоящее либо кажущееся присутствие в созданных человеком объектах (от кредитных карточек до рисунка Леонардо да Винчи «Витрувианский человек»), но его проявления в природе (рост цветов и ракушек, к примеру).
Вычисление золотого соотношения
Существует большое количество способов математически выразить золотое соотношение, и во всех этих методах имеется своя определенная простота, точность и обаяние. Эвклид обрисовывал его как «сечение в крайнем и среднем отношении». Более «математичное» выражение выглядит так: если золотое соотношение равняется х, то х/1 = 1/(х -1), где x > 1 – есть длина стороны, которая разделена на два неравных отрезка (в простейшем случае больший отрезок равен 1, меньший отрезок получается x – 1 ). Или мы получаем следующее уравнение золотого сечения: х² – х – 1 = 0. Словами же золотое соотношение определяют как пропорцию, в которой «протяженность всей линии относится к большей ее части так же, как та — к меньшей».
Хороший пример золотого сечения — кредитная карточка, имеющая однообразные стандартные размеры во всем мире. В соответствии с правилами золотого соотношения, отношение ее маленькой стороны к длинной такое же, как отношение длинной к сумме длин короткой и длинной сторон. Это делает кредитку золотым прямоугольником. Такая форма была выбрана из-за своего сбалансированного вида — она не кажется ни через чур длинной, ни через чур широкой. Один из способов проверить, есть ли прямоугольник золотым, — расположить два прямоугольника рядом, один «поставив» вертикально на маленькую грань, другой «положив» прикасаясь к первому на долгую. Если диагональ, проходящая через углы расположенного горизонтально прямоугольника, продолжившись, достигнет верхнего угла прямоугольника, расположенного вертикально, прямоугольники являются золотыми. Значительно чаще данный принцип видится в архитектуре. Так, золотым прямоугольником является фасад здания ООН в Нью-Йорке.
Математика в искусстве и природе
В золотом соотношении есть что-то прозаичное — по крайней мере, для тех, кто не владеет математическим складом ума. Речь идет о его численном выражении. Значение х в алгебраическом выражении х² – х – 1 = 0 равняется 1,6180339887… и так без конца. Однако золотое соотношение имеет самое прямое отношение к западному искусству. В большой степени эта связь появилась благодаря трудам Луки Пачоли на рубеже XVI в. Пачоли был современником Леонардо да Винчи, и кое-какие из рисунков маэстро — включая наиболее известное изображение Витрувианского человека — появляются в книге Пачоли De Divina Proportione («Божественная пропорция»), изданной в 1509 г. В данной книге заложены базовые геометрические правила красоты, а вдохновлялся создатель числом фи. Так, в совершенных пропорциях человеческого тела соотношение роста до пупка и полного росту есть золотым. К сожалению, фактические измерения говорят о том, что в действительности «совершенных» тел фактически нет. В ХХ в. золотое соотношение высматривали в естественных формах. Те, кто делал это достаточно упорно, находили его в пропорциях листьев, распределении бутонов на стебле (природные закономерности скорее приблизительно подчиняются принципу последовательности Фибоначчи), кроме того в траектории пикирования охотящегося ястреба. Для кого-то это являлось свидетельством в пользу существования некоего замысла, в соответствии с котором организована сама природа. Для других же это означало, что наше восприятие красоты (либо, по крайней мере, приятной для глаз пропорциональности) продиктовано математикой роста, которая представляет повышение структур в размерах без утраты ими общей формы.
Золотая спираль
Спираль, разворачивающуюся в соответствии с принципом золотого соотношения, возможно выстроить посредством серии золотых прямоугольников. Это частный случай логарифмической спирали, расходящейся от осевой точки под постоянным углом (Математически более верно формулировать так: кривая, касательная к которой образует с радиус-вектором в каждой точке один и тот же угол). Эту спираль соотносят с именем Якоба Бернулли (не смотря на то, что первым обрисовал ее Декарт), главным исследователем ее свойств. Бернулли кроме того захотел, чтобы такую спираль выгравировали на его надгробии, но плохо подкованный в геометрии каменщик воспроизвёл там Архимедову спираль с более пологой траекторией расхождения.
Немного фактов
Интересный факт о золотом сечении №1. Пропорции соседних сегментов раковины моллюска наутилуса приближаются к золотому соотношению.Интересный факт о золотом сечении №2. Не обращая внимания на то, что свое обозначение золотое соотношение взяло в честь Фидия, он не руководствовался этим принципом при разработке проекта Парфенона. Храм немного высоковат чтобы его пропорции строго отвечали стандарту золотого сечения — то ли из-за ошибки в расчетах, то ли вследствие того что Фидию так больше нравилось.
Интересный факт о золотом сечении №3. Золотые прямоугольники возможно поделить на нескончаемое количество уменьшающихся в размерах золотых прямоугольников, «отрезая» от них части по кратчайшей линии. В терминологии греческой школы математиков такое свойство делает золотой прямоугольник гномоном — объектом, способным сохранять форму по мере роста (либо уменьшения).
Интересный факт о золотом сечении №4. Кредитная карточка является примером золотого прямоугольника. Также золотым прямоугольником является фасад здания ООН в Нью-ЙоркеИнтересный факт №5. Фактические измерения говорят о том, что в действительности «совершенных» тел, удовлетворяющих правилу золотого сечения фактически нет.Интересный факт №6. Бернулли хотел, чтобы золотую спираль выгравировали на его надгробии, но плохо подкованный в геометрии каменщик воспроизвёл там Архимедову спираль с более пологой траекторией расхождения.
Наша библиотека в telegram (много книг для физиков, математиков и программистов) : https://t.me/physics_lib
Еще много полезного и интересного вы сможете найти на наших ресурсах:
Physics.Math.Code в контакте (VK)
Physics.Math.Code в telegram
Physics.Math.Code в YouTube
Репетитор IT mentor в VK
Репетитор IT mentor в Instagram
Репетитор IT mentor в Яндекс.Дзен



![{displaystyle varphi ={frac {1}{Phi }}={frac {{sqrt {5}}-1}{2}}=e^{-0,2ipi }+e^{0,2ipi }=e^{-0,2ln -1}+e^{0,2ln -1}=(-1)^{-0,2}+(-1)^{0,2}={frac {1}{sqrt[{5}]{-1}}}+{sqrt[{5}]{-1}}=2{mathfrak {R}}({sqrt[{5}]{-1}})approx 0,61803}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fdc65998e194179675ce0e4dd70cc137c00e6175)








