Эдс как найти производная

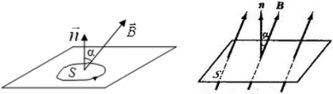
Магнитный поток, проходящий через площадь S равен:

Ф = BScosα;

где:

Ф ― величина магнитного потока [Вб],

S ― площадь контура [м2],

B ― индукция магнитного поля [Тл],

α ― угол между нормалью $overrightarrow{n}$ к площади контура и вектором индукции магнитного поля $overrightarrow{B}$.

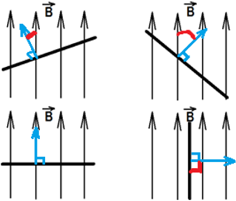
Если вектор индукции магнитного поля $overrightarrow{B}$ перпендикулярен площади контура, то магнитный поток равен:

Ф = BScos90° = BS;

Максимальное значение потока будет тогда, когда косинус будет максимальным (cosα = 1), то есть угол между вектором $overrightarrow{B}$ и вектором нормали к пластинке равен 0°, чему соответствует картинка 3. Наименьшее же значение потока будет тогда, когда косинус будет равен нулю (cosα = 0), то есть угол между нормалью к пластинке и вектором индукции равен 90°, чему соответствует картинка 4.

Электромагнитная индукция ― явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через контур. Если контур разомкнут, то на его концах наблюдается разносность потенциалов, равная ЭДС индукции.

ЭДС электромагнитной индукции возникает только тогда, когда изменяется магнитный поток.

Закон Фарадея об электромагнитной индукции и гласит, что индуцируемая ЭДС прямо пропорциональна скорости изменения магнитного потока:

$varepsilon_i = -frac{Delta text{Ф}}{Delta t}$

где:

$varepsilon_i $ ― ЭДС электромагнитной индукции [B],

$frac{Delta text{Ф}}{Delta t}$ ― скорость изменения магнитного потока [Вб/с],

∆Ф ― изменение магнитного потока [Вб],

∆t ― время, за которое происходит это изменение [c].

Кроме того, ЭДС индукции равна производной магнитного потока по времени:

$varepsilon_i = -text{Ф}_t’$

где:

• ― ЭДС электромагнитной индукции [B],
• ― производная магнитного потока по времени [Вб/с].

Задача 1

Замкнутый контур площадью S из тонкой проволоки помещён в магнитное поле. Плоскость контура перпендикулярна вектору магнитной индукции поля. В контуре возникают колебания тока с амплитудой iм = 35 мА, если магнитная индукция поля меняется с течением времени в соответствии с формулой B = acos (bt), где a = 6 · 10-3Тл, b = 3500 c-1. Электрическое сопротивление контура R = 1,2 Ом. Чему равна площадь контура?

Решение:

Обратите внимание на величины, данные в условии. Они здесь совсем не такие, к которым вы привыкли, потому что не дано значение магнитного поля, а дана зависимость магнитного поля от времени. Посмотрим, как это скажется на решении задачи.

Поскольку магнитное поле, а вместе с ним и поток меняются, то будет возникать ЭДС индукции, именно это ЭДС и вызовет электрический ток, поэтому запишем закон электромагнитной индукции.

По закону электромагнитной индукции $varepsilon_i = -frac{Delta text{Ф}}{Delta t}$

ЭДС — это изменение магнитного потока за время. Ничего в определении ЭДС не сказано про это самое время. Дело в том, что изменение какой-то величины за небольшой промежуток времени называется производной по времени. То есть наше ЭДС, которое является изменением магнитного потока за небольшой промежуток времени, это просто производная магнитного потока по времени $varepsilon_i = -text{Ф}_t’$

И это очень важный момент, без которого мы не сможем решить такого рода задачу.

Теперь посчитаем ЭДС индукции.

Напишем, чему равен магнитный поток Ф = BS = acos (bt) · S.

ЭДС индукции — это производная магнитного потока по времени. Теперь придётся вспомнить немного математики. Множители “a” и “S” перед косинусом не зависят от времени, поэтому производная их не трогает, а вот у косинуса в скобках стоит зависимость от времени, поэтому именно от косинуса производную и нужно взять.

Обратите внимание на полученную формулу магнитного потока. В ней стоит просто множитель aS перед сложной функцией косинуса

$text{Ф} underset{text{множитель}}{underbrace{aS}} ;; cdot ;; underset{text{сложная функция}}{underbrace{cos(bt)}}$.

Взяв производную от этой функции, получаем Ф´ = –abS · sin (bt). А теперь, раз мы знаем производную магнитного потока, значит, знаем и ЭДС индукции, потому что $varepsilon_i = -text{Ф}_t’$

Подставив сюда значение производной, получим $varepsilon_i = -text{Ф}_t’$ = abS · sin (bt).

Мы получили значение ЭДС. Кроме этого, мы знаем сопротивление и максимальную силу тока, поэтому запишем закон Ома.

По закону Ома $I = frac{varepsilon}{R}$ , подставив сюда значение ЭДС, получаем $I = frac{abScdot sin(bt)}{R}$.

Мы получили зависимость силы тока от времени.

Из-за синуса, который стоит в этой формуле, ток постоянно меняет свое значение, то он становится больше, то меньше, поскольку синус меняет своё значение от -1 до 1.

В условии дано максимальное значение силы тока, которое протекает по контуру. Когда эта величина будет максимальной? В тот момент, когда синус будет максимальным, то есть равный единице. Поэтому запишем sin (bt) = 1.

Максимальное значение тока будет в тот момент, когда будет максимальным значение ЭДС индукции, то есть когда, $I_{max} = frac{abS}{R}$.

Отсюда можно легко выразить площадь контура $S = frac{I_{max}R}{ab}$, подставив сюда все значения, получим $S = frac{I_{max}R}{ab} = frac{35cdot 10^{-3} Acdot 1,2text{Ом}}{6cdot 10^{-3}text{Тл} cdot 35000c^{-1}} = 0,002text{м}^2$

Ответ: 0,002

Как видно из формулы магнитного потока Ф = BScosα, изменение магнитного потока может быть вызвано разными факторами:

• увеличением или уменьшением модуля индукции магнитного поля (т. е. величины $frac{Delta B}{Delta t}$);
• изменением направления вектора магнитного поля (т. е. изменением угла α);
• деформацией контура, причем такой деформацией, при которой изменяется площадь контура (т. е. изменением величины $frac{Delta S}{Delta t}$ );
• изменением нескольких из этих величин одновременно.

Таким образом, изменение модуля или направление вектора магнитной индукции или площади контура неизбежно приводят к тому, что в контуре возникает электродвижущая сила.

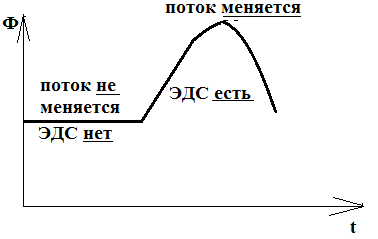
Если нарисовать график зависимости магнитного потока, то он может выглядеть либо так: тогда поток не будет менятьсяи ЭДС не возникает.

Либо так, тогда будет меняться поток и возникать ЭДС:

Знак «минус» перед скоростью изменения магнитного потока в формуле отражает правило Ленца: индуцированный ток всегда направлен так, чтобы магнитное поле, которое он создает, препятствовало изменению магнитного потока.

Если магнитный поток, проходящий через площадь контура, уменьшается, то магнитное поле индуцированных токов будет стремиться его увеличить.

Если поток увеличивается ― магнитное поле индуцированных токов будет стремиться его уменьшить.

Задача 2

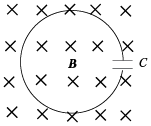
Два проводящих кольца расположены относительно проводника с током в одной плоскости, как это показано на рисунке. В каком направлении будет индуцироваться ток в этих кольцах, если начать двигать их в направлении проводника?

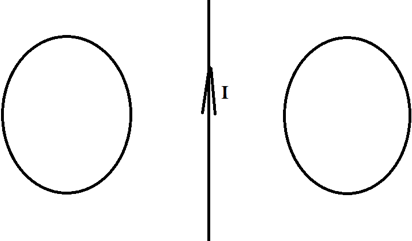
Решение:

Первым делом необходимо понять, как вообще может возникать индуцированный ток, если даже магнитного поля нет?

Его направление мы можем определить по правилу правого винта. Отметим это на рисунке.

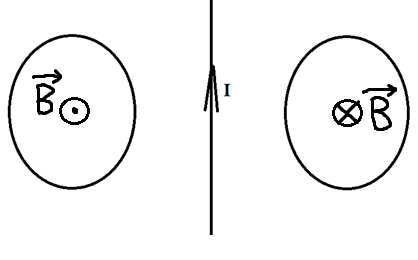
Теперь эти два проводника начинают двигать. Разве от этого меняется поток? Ведь площадь остаётся та же самая, угол между нормалью и вектором тоже не меняется. Однако, чем ближе к проводнику с током, тем сильней поле, а чем дальше от него, тем слабее! Поэтому, когда мы двигаем кольца к проводнику, мы увеличиваем поток, ведь ближе поле сильнее. Значит, будет появляться ток, а его направление можно определить по правилу Ленца. Что нам говорит правило Ленца?

Раз поток увеличивается, то по правилу Ленца ток будет индуцироваться так, чтобы уменьшить поток, то есть магнитное поле в левом кольце будет направлено от нас, а в правом ─ на нас. А значит, по правилу правого винта мы можем определить, что ток будет течь по часовой стрелке слева и против часовой стрелки справа.

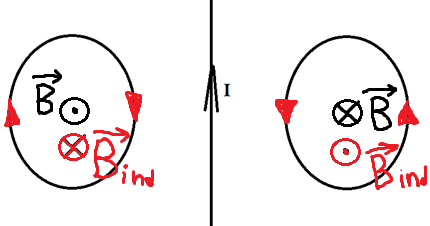
Движение проводников

Если к концам проводника, движущегося в магнитном поле, подключить вольтметр, то прибор покажет наличие разности потенциалов на концах проводника. Таким образом, когда проводник перемещается в области с магнитным полем, в нем возникает электромагнитная движущая сила (ЭДС).

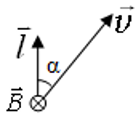
Согласно закону Лоренца, в проводнике, движущемся в магнитном поле, создается ЭДС $|varepsilon_i| = Blvsinalpha$;

где:

$varepsilon_i$― ЭДС электромагнитной индукции [B],

B ― индукция магнитного поля [Тл],

l ― длина проводника [м],

v ― скорость движения проводника [м/с],

α ― угол между направлением вектора скорости $overrightarrow{v}$ и длиной проводника $overrightarrow{l}$ , если вектор индукции магнитного поля $overrightarrow{B}$перпендикулярен проводнику и вектору скорости его движения: $overrightarrow{B} perp overrightarrow{v}, overrightarrow{B} perp overrightarrow{l}$

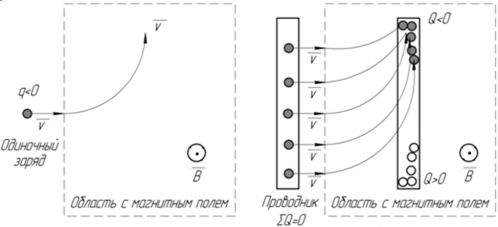
Используя силу Лоренца, можно получить это определение ЭДС. Сила Лоренца ― это проявленное действие магнитного поля на заряженную частицу.

В проводнике присутствует большое количество свободных зарядов (именно это отличает проводники от диэлектриков), и на каждый из зарядов действует сила Лоренца, перемещая их по проводнику так, что в одной его части скапливается отрицательный заряд, а в другой, соответственно, положительный. Это распределение зарядов и является физической основой для возникновения электродвижущей силы.

На рисунке показано как сила Лоренца, действующая на каждый из зарядов проводника, создаёт ЭДС в проводнике. Если одиночный отрицательный заряд попадает в магнитное поле, направленное от нас, то, согласно правилу левой руки, направление его движения изменяется так, как показано на рисунке. Если в область с таким же магнитным полем входит проводник, суммарный заряд которого равен нулю, но внутри которого находятся электроны, способные свободно перемещаться в проводнике, то электроны стекаются в один конец проводника. Так как электроны переместились в один конец проводника, то этот конец приобретает отрицательный заряд, а противоположный ему ― положительный. Таким образом, в проводнике возникает разность потенциалов и электродвижущая сила.

В некоторых случаях удобно решать задачи, используя определение ЭДС через закон Лоренца (обычно это задачи о движении прямолинейного проводника в поле), в других ― через закон Фарадея.

В проводнике, движущемся в магнитном поле, образуется разность потенциалов U = lvBsinα;

где:

U — разность потенциалов [В],

l — длина проводника [м],

v — скорость движения проводника $big[ frac{text{м}}{c} big]$

B — индукция магнитного поля [Тл],

α — угол между направлением скорости и длиной проводника.

В случае, если есть какой-то замкнутый контур, то ЭДС в нем возникает только тогда, когда меняется магнитный потокчерез этот контур. В случае же тонкого стержня, для которого нельзя применить понятия магнитного потока, потому что у него просто нет площади, ЭДС возникает при движении в постоянном магнитном поле.

В случае, если в задаче дана проводящая рамка или контур, для определения ЭДС (напряжения) используем формулу $varepsilon_i = – frac{Delta text{Ф}}{Delta t}$

В случае, если в задачи дан проводник, движущейся в поле, для определения ЭДС (напряжения) используем формулу $varepsilon$ =U= lvBsinα.

Задача 3

В заштрихованной области на рисунке действует однородное магнитное поле, перпендикулярное плоскости рисунка с индукцией В = 0,1 Тл. Квадратную проволочную рамку, сопротивление которой 10 Ом и длина стороны 10 см, перемещают в этом поле в плоскости рисунка поступательно равномерно с некоторой скоростью υ. При попадании рамки в магнитное поле в положении 1 в ней возникает индукционный ток, равный 1 мА. Какова скорость движения рамки?

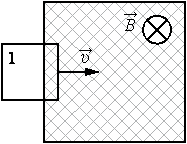
Решение:

Составим цепочку.

Зная силу тока и сопротивление, что можно найти? Мы сможем найти напряжение, то есть ЭДС, а ЭДС, уже можно легко связать со скоростью движения рамки.

Составим цепочку. Мы знаем магнитное поле (В), длину стороны (a), сопротивление (R) и силу тока (I), а найти нужно скорость(v).

Зная ток и сопротивление, что сразу можно найти? Напряжение, то есть ЭДС, которое мы сможем найти по закону Ома.

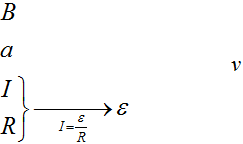
А связать ЭДС с индукцией поля, стороной рамки и скоростью движения очень легко, воспользовавшись той формулой, которую мы получили в прошлой задаче.

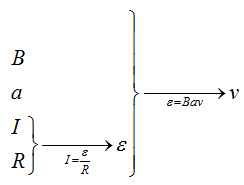
Пройдёмся вдоль этой цепочки.

Запишем закон Ома $I = frac{varepsilon}{R}$, подставив сюда формулу для ЭДС, которую мы получили в прошлой задаче, отбросив знак «минус» получим $I = frac{varepsilon}{R} = frac{Bav}{R}$отсюда выразим скорость, и, подставив все величины, получим $v = frac{IR}{Ba} = frac{1cdot 10^{-3} Acdot 10text{Ом}}{0,1 text{Тл} cdot 0,1 text{м}} = 1 frac{text{м}}{c}$

Ответ: 1

Электричество рождает магнетизм

Сперва Эрстед в Дании, а потом Ампер с коллегами во Франции в начале XIX века собрали немало свидетельств воздействия электрического тока на магниты: стрелка компаса поворачивалась, если рядом протекал ток, линейный магнит втягивался в соленоид, сталь намагничивалась, будучи помещенной в катушку с током и т.п. Даже утвердилось мнение, что все эффекты, демонстрируемые с постоянными магнитами, можно воспроизвести, создавая электрический ток соответствующей силы и конфигурации или, иначе говоря, магнитные поля возбуждаются движущимися электрическими зарядами.

… а магнетизм – электричество!

Также было установлено, что магнитное поле действует на движущийся электрический заряд (см. сила Ампера и сила Лоренца), но вот доказательств того, что магнитное поле может воздействовать на неподвижный электрический заряд, долгое время получить не удавалось, но многие предполагали – хотя бы в силу симметрии! – что такое воздействие должно существовать. Честь открыть его выпала великому англичанину Майклу Фарадею: он экспериментально установил, что на электрический заряд действует меняющееся магнитное поле, или – другими словами – меняющееся магнитное поле порождает электрическое поле.

Формула и правило

Наиболее изящным выражением закона электромагнитной индукции Фарадея является следующая формула:

E=−dФdtE = – frac{dtext{Ф}}{dt},

где EE – электродвижущая сила (ЭДС), возникающая в замкнутом контуре,

Фtext{Ф} – поток вектора магнитной индукции через поверхность, натянутую на этот контур.

Другими словами ЭДС в контуре есть производная магнитного потока, взятая с обратным знаком.

Представляется, однако, что для лучшего понимания явления необходимо сделать пару пояснений.

Первое: поток Фtext{Ф} вектора (в данном случае вектора B‾overline{B}) через поверхность – математическое понятие, это есть сумма произведений BΔScos⁡αBDelta Scos{alpha}, где ΔSDelta S – очень маленький плоский элемент поверхности, BB – модуль вектора в точках этого элемента, а αalpha – угол между нормалью к выбранному элементу и направлением вектора B‾overline{B}. Например, если поле однородно, а контур – окружность радиуса RR, ограничивающая круг, плоскость которого перпендикулярна вектору B‾overline{B}, то поток вектора через круг Ф=BπR2text{Ф} = B pi R^2.

Второе: ЭДС, обусловленная сторонними силами, которыми в данном случае являются силы электрического поля, созданного не зарядами, а изменением магнитного поля, возбуждает в замкнутом контуре электрический ток, чье направление задается знаком минус в вышеприведенной формуле закона Фарадея. Но практически проще и физически осмысленнее (и глубже) определять его, опираясь на правило Ленца: индукционный ток производит магнитное поле, призванное компенсировать изменение потока вектора магнитной индукции исходного поля, породившее ток. К примеру, если поток индукции исходного поля уменьшается, то ток потечет таким образом, что порожденное им магнитное поле будет увеличивать поток результирующего (т.е. суммы векторов исходного и возникшего полей) вектора магнитной индукции.

Как этим пользоваться. Задача

Рассмотрим следующую задачу.

В одной плоскости расположены две квадратные рамки, изготовленные из одной и той же проволоки, причем на меньшую рамку пошло вполовину меньше провода. Сила тока, наведенная в большей рамке при изменении магнитного поля, составляет 2A2A. Какова сила тока, наведенная в меньшей рамке?

Дано:
п=2text{п}=2
I=2AI=2A
i=?i = ?

Решение

По закону электромагнитной индукции ЭДС в контуре E=−dФdtE = -frac{dtext{Ф}}{dt}, Фtext{Ф} – поток вектора магнитной индукции через рамку. Рамки квадратные, а значит площадь меньшей из них меньше в 4 раза, как и производная потока Фtext{Ф}, а значит и ЭДС Е (считаем магнитное поле однородным). Ток в рамке есть отношение ЭДС к сопротивлению рамки, у меньшей рамки оно вдвое меньше, соответственно i=0,25E0,5R=0,5I=1Ai=frac{0,25E}{0,5R} = 0,5I = 1A.

Ответ: i=0,5I=1Ai = 0,5I = 1A.

Тест по теме «Закон электромагнитной индукции Фарадея»

Обновлено: 19.05.2023

Рассматривая физический смысл производной (см. §42 данного справочника), мы выяснили, что:

Например:
Рассмотрим прямолинейное равноускоренное движение.
Уравнение этого движения имеет вид: $$ x(t)=x_0+v_0t+frac $$ где (x(t)) – ккордината тела в произвольный момент времени (t, x_0) – начальная координата, (v_0) – начальная скорость, (a=const) – ускорение, действующее на тело.
Чтобы найти скорость тела из этого уравнения, нужно найти производную от координаты по времени: $$ v(t)=x'(t)=left(x_0+v_0t+fracright)’=0+v_0cdot 1+frac a2cdot 2t=v_0+at $$ Чтобы найти ускорение, нужно найти производную от скорости: $$ a(t)=v'(t)=x”(t)=(v_0+at)’=0+acdot 1=a=const $$

п.2. Физические величины как производные от других величин

Если рассматривать уравнение процесса (s=f(t)), его производной будет величина $$ f'(t)=lim_frac $$ Такие величины часто встречаются в различных разделах физики и техники.

Угол поворота (varphi(t))

Угловая скорость (omega(t)=omega'(t))
Угловое ускорение (beta(t)=omega'(t)=varphi”(t))

Масса горючего ракеты (m(t))

Скорость расходования горючего (u(t)=m'(t))

Температура тела (T(t))

Скорость нагрева (v_T(t)=T'(t))

Магнитный поток (Ф(t))

ЭДС индукции (varepsilon(t)=-Ф'(t))

Число атомов радиоактивного вещества (N(t))

Скорость радиоактивного распада (I(t)=-N'(t))

Конечно же, в физике далеко не обязательно берут производную только по времени.
Например, для теплоты Q(T) теплоемкость равна C(T)=Q'(T), где T – температура.
А для процесса теплопереноса температура u(x,t) в точке с координатой x в момент времени t определяется уравнением теплопроводности: $$ frac<partial u(x,t)><partial t>-a^2frac<partial^2 u(x,t)><partial x^2>=f(x,t) $$ и производные берутся по времени (left(frac<partial u><partial t>right)) и по координате (left(frac<partial u><partial x>right)), причем по координате берется производная второго порядка (left(frac<partial^2 u><partial x^2>right)).
Поэтому в физике для производных чаще используются обозначения Лейбница, в которых хорошо видна как функция, так и аргумент.
Например, для производных функции от одной переменной: (frac<partial varphi><partial t>, frac<partial p><partial V>, frac<partial Q><partial T>. )
Для производных функций от многих переменных: (frac<partial u><partial t>, frac<partial u><partial x>, frac<partial u><partial y>, frac<partial u><partial z>. )

п.3. Примеры

Пример 1. Тело массой 6 кг движется прямолинейно по закону (x(t)=t^2+t+1) (м). Найдите: 1) кинетическую энергию тела через 3 с после начала движения; 2) силу, действующую на тело в это время.
1) Кинетическая энергия равна (E=frac)
Скорость тела: (v(t)=x'(t)=(t^2+t+1)’=2t+1)
Через 3 с: (v(3)=2cdot 3+1=7) (м/с)
Подставляем: (E=frac=147) (Дж)

2) Сила по второму закону Ньютона: (F=ma)
Ускорение тела: (a(t)=v'(t)=(2t+1)’=2) (м/с^2)
Ускорение постоянно.
На тело действует постоянная сила: (F=6cdot 2=12) (Н)

Ответ: 147 Дж; 12 Н

Пример 2. Маховик вращается по закону (varphi (t)=4t-0,5t^2) (рад)
Найдите момент времени, в который маховик остановится.

Угловая скорость: (omega(t)=varphi ‘(t)=(4t-0,5t^2 )’=4-0,5cdot 2t=4-t)
В момент остановки угловая скорость равна 0. Решаем уравнение: $$ 4-t=0Rightarrow t=4 (c) $$ Ответ: 4 c

Пример 3. Ракету запустили вертикально вверх с начальной скоростью 40 м/с. В какой момент времени и на какой высоте ракета достигнет наивысшей точки (g≈10м/с 2 )?

Выберем начало отсчета на земле ((y_0=0)), направим ось y вверх.
Начальная скорость направлена вверх, её проекция на ось положительна.
Ускорение свободного падения направлено вниз, его проекция отрицательна.
Уравнение движения: $$ y(t)=y_0+v_t+frac=0+40t-frac=40t-5t^2 $$ В верхней точке траектории ракета останавливается, её скорость равна 0.
Найдем скорость: $$ v(t)=y'(t)=40-5cdot 2t=40-10t $$ Найдем момент остановки в верхней точке: $$ 40-10t_0=0Rightarrow t_0=frac=4 (c) $$ Найдем высоту подъема в верхней точке: $$ H_=y(t_0)=40cdot 4-5cdot 4^2=80 (м) $$ Ответ: 4 с, 80 м

Пример 4. Через поперечное сечение проводника проходит заряд (q(t)=ln⁡(t+1)) (Кл). В какой момент времени сила тока в проводнике равна 0,1 А?

Сила тока: $$ I(t)=q'(t)=(ln(t+1))’=frac $$ По условию: $$ frac=0,1Rightarrow t_0+1=frac=10Rightarrow t_0=9 (c) $$ Ответ: 9 c

Пример 5. Колесо вращается так, что угол его поворота пропорционален квадрату времени. Первый оборот оно сделало за 8 с. Найдите угловую скорость через 48 с после начала вращения.

По условию угол поворота (varphi (t)=At^2)
Один оборот (2pi) радиан был сделан за 8 с. Получаем уравнение: (Acdot 8^2=2pi)
Находим коэффициент (A=frac<2pi>=frac<pi>)
Уравнение движения (varphi(t)=frac<pi>t^2) (рад)
Угловая скорость (omega(t)=varphi ‘(t)=left(frac<pi>t^2right)’=frac<pi>cdot 2t=frac<pi>t) (рад/с)
Через 48 секунд (omega(48)=frac<pi>cdot 48=3pi) рад/с – полтора оборота в секунду.
Ответ: (3pi) рад/с

Пример 6. Для нагревания 1 кг жидкости от 0°С до t°C необходимо (Q(t)=1,7t+at^2+bt^3) Дж теплоты.
Известно, что теплоемкость жидкости при температуре 100°С равна 1,71 Дж/К, а для нагревания 1 кг этой жидкости 0°С до 50°C требуется 85,025 Дж теплоты. Найдите коэффициенты a и b.

Теплоемкость: (C(t)=Q'(t)=1,7cdot 1+acdot 2t+bcdot 3t^2=1,7+2at+3bt^2)
По условию: begin C(100)=1,7+2acdot 100+3bcdot 100^2-1,71\ 200a+30000b=0,01 end Кроме того: begin Q(50)=1,7cdot 50+acdot 50^2+bcdot 50^3=85,025\ 2500a+125000b=0,025 end Получаем линейную систему: begin begin 200a+30000b=0,01 |:2\ 2500a+125000b=0,025 |:25 end Rightarrow begin 100a+15000b=0,005\ 100a+5000b=0,001 end \ 15000b-5000b=0,005-0,001\ 10000b=0,004\ b=4cdot 10^cdot 10^=4cdot 10^ left(fracright)\ a=frac=frac<10^-5cdot 10^3cdot 4cdot 10^>=frac<10^-2cdot 10^>=-frac<10^>\ a=-10^ left(fracright) end Ответ: (a=-10^frac; b=4cdot 10^frac)

Пример 7*. Лестница длиной 5 м стояла вертикально. Потом её нижний конец стали перемещать по полу с постоянной скоростью (v=2) м/с. С какой по абсолютной величине скоростью в зависимости от времени опускается верхний конец лестницы? Постройте график полученной функции.

Лестница со стенами образует прямоугольный треугольник, для которого справедлива теорема Пифагора: $$ x^2(t)+y^2(t)=5^2 $$ Нижний конец движется с постоянной скоростью, его уравнение движения по полу: $$ x(t)=vt=2t $$ Отсюда получаем уравнение движения верхнего конца по стенке: begin y^2(t)=25-x^2(t)=25-(2t)^2=25-4t^2\ y(t)=sqrt end

6) Пересечение с осями
В начале координат: (t=0, u=0)

7) График

Пример 8. Под действием нагрузки деталь с поперечным сечением в виде прямоугольника площадью 17 см 2 начинает деформироваться. Одна из сторон прямоугольника растет с постоянной скоростью 1 см/ч, а вторая – уменьшается со скоростью 0,5 см/ч. Найдите скорость изменения площади поперечного сечения через 45 мин после начала деформации, если известно, что в этот момент его площадь равна 20 см 2 .

Тип урока: Закрепление и совершенствование знаний по математике и физике.

Цели урока: Закрепление понятия физического смысла производной, рассмотрение использования механического истолкования производной при решении задач, связанных с физическим смыслом.

Организационная информация

Применение производной в математике и физике.

Физика и математика

Автор урока (ФИО, должность)

Жукова Елена Владимировна, учитель физики,

Матвейчук Лидия Николаевна, учитель математики

Республика Карелия, г. Олонец

Методическая информация

Закрепление и совершенствование знаний по математике и физике.

Закрепить понятие физического смысла производной, рассмотреть использование механического истолкования производной при решении задач, связанных с физическим смыслом.

дать понятие о возможностях применения элементов дифференциального исчисления в описании и изучении процессов и явлений реального мира;

показать широкий спектр приложений производной;

расширить знания учащихся о производной первого и второго порядка, используя ее физический смысл;

развивать логическое мышление при установлении связи физических величин с понятием производной;

развивать монологическую речь в ходе объяснений, обоснований выполняемых действий;

развивать навыки самостоятельной работы, работы с компьютером, тестам.

Знания, умения, навыки и качества, которые актуализируют/приобретут/закрепят/др. ученики в ходе урока

В ходе урока учащиеся повторяют определение производной, а затем формулы – производная линейной функции, производная степенной функции, производные тригонометрических функций – синуса и косинуса, производную сложной функции и производную произведения, повторяют геометрический смысл производной, а также физический смысл производной первого и второго порядка.

Применение элементов дифференциального исчисления в описании и изучении процессов и явлений реального мира осуществляется при решении задач различного плана: на равноускоренное движение, на нахождение работы, ЭДС индукции и самоиндукции и другое.

Необходимое оборудование и материалы

Компьютер, экран, мультимедиа, раздаточный материал в виде тестов.

Подробный конспект урока

Практическое применение производной.

Ход и содержание урока

Организационный момент

Учитель математики формулирует тему и цели урока (Слайд 1, 2).

Ученики записывают число и тему урока в тетрадях.

Повторение определения производной и её геометрического и физического смысла

1) Сформулируйте определение производной.

На экране появляется запись определения и формула:

f ′ ( x )= (слайд 3).

2). На экране появляется слайд, содержащий информацию о происхождении терминологии и условных обозначениях, принятых в математике и физике для обозначения производной (слайд 4).

3). Учитель предлагает учащимся вспомнить формулы – производная линейной функции, производная степенной функции, производные тригонометрических функций – синуса и косинуса, производную сложной функции и производную произведения. Эти формулы появляются на экране (слайд 5).

Устная работа.

4). Устно решить следующие задания:

найти производную функций

1). Х 2 + 4Х 2). Х/3 – sinX

3). X 8 /4 + LnX 4). 5X -3 – 1/X

5). – 6X 4 + π 6). X sinX

7). X 2 cosX 8). СOS 2 (3X+4)

5) В чем заключается геометрический смысл производной? (слайд 6).

5). Повторение физического смысла производной первого и второго порядка (слайд 7).

Решение задач по механике. (Решают с учителем физики).

Учащимся предлагается решить 4 задачи по механике в тетради и сравнить полученный ими ответ и решение с предложенным решением на следующих слайдах.

Координата материальной точки изменяется с течением времени по закону х(t)=3t 2 –7t + 6, где t – время движения в секундах. Найдите скорость точки в момент времени t = 6c (слайд 9).

При движении тела по прямой его скорость V меняется по закону V ( t ) = t 5 /5 – t 3 + + t + 1 , где t – время движения в секундах. Найдите ускорение (м/с 2 ) через 2 секунды после начала движения (слайд 10).

Найдите силу F , действующую на тело массой m, движущегося прямолинейно по закону х( t ) = 2t 3 – t 2 , где t – время движения в секундах, при t = 2с (слайд 11).

Точка движется вдоль оси ОХ, координата ее меняется в соответствии с уравнением Х = (5t 3 – 4t + 8), где t – время в секундах. Масса точки равна 3 кг. Определите значение кинетической энергии тела через 1 с после начала движения (слайд 12).

Следующую задачу учащиеся решают на доске и в тетради:

Проекция скорости материальной точки вдоль оси ОХ изменяется по закону Vx= 2t. Какую работу совершает сила, действующая на эту точку за 5 секунд, если ее масса равна 2 кг (слайд 13).

Механическая работа находится по формуле: А=FScosα

Силу находим в соответствии со вторым законом Ньютона, по формуле F = ma. Ускорение – производная функции Vx = 2t., путь S – ее первообразная. Подставив числовые значения из данных задачи, получаем ответ 100 Дж.

Решение задач для закрепления физического смысла производной. (Решают с учителем математики).

Лампа подвешена на высоте 12 метров над прямой горизонтальной дорожкой, по которой идет человек ростом 1,8 м. С какой скоростью удлиняется его тень, если он удаляется от лампы со скоростью 50 м/мин.? (слайд 14).

На рисунке: ОА – высота, на которой находится лампа, MN – рост человека, МР – длина тени (Зависит от времени t).

Пусть t – время движения человека, выраженное в минутах. Тогда 50t метров – длина отрезка ОМ (это расстояние, на которое удаляется человек от лампы). Рассмотрим треугольники OАP и MNP. Они прямоугольные, подобные. Из подобия треугольников следует пропорциональность сторон OА/MN = OP/PM. Подставив в пропорцию данные, получаем 12/1,8 = (50t+PM)/PM. Решая пропорцию, находим длину тени РМ. РМ = 150t/17, метров. Закон изменения, т.е. скорость удлинения тени V = 150/17, м/мин.

Два тела начали движение по прямой одновременно из одной точки. Скорость первого V(t) = 3t 2 – 6t, второго V(t) = 10t + 20. В какой момент времени и на каком расстоянии от начальной точки произойдет их встреча? (Скорость измеряется в метрах в секунду.) (слайд 15).

Пройденный путь есть первообразная скорости. Значит, S₁(t) = t 3 – 3t 2 , S₂(t) = 5t 2 + 20t. По условию задачи известно, что S₁ = S₂. Решаем уравнение t 3 – 3t 2 = 5t 2 + 20t. Корнями уравнения являются числа 0, -2 и 10. Т.к. t ≥ 0, то t = 10 секунд. Следовательно, S₍₁₀₎₌700 метров.

Ответ: через 10 секунд, 700 метров.

Решение задач по электромагнетизму. (Решают с учителем физики).

Величина вектора индукции однородного магнитного поля меняется по закону В = (0,15+0,1t) Тл, где t- время в секундах. Найти в милливольтах ЭДС индукции в круговом контуре площадью 0,05м 2 , расположенном в данном поле перпендикулярно к линиям индукции. (слайд 17).

Для нахождения ЭДС индукции производную вектора магнитной индукции надо умножить на площадь контура: 0,1*0,05 – 0,005 В = 5мВ.

Поток магнитной индукции через проводящий контур меняется по закону Ф = (2 + 0,05t) Вб. Чему равна величина силы индукционного тока в контуре, если его сопротивление 2,5 Ом? (слайд 18).

Для нахождения силы индукционного тока в контуре надо, в соответствии с законом Ома, величину ЭДС индукции разделить на сопротивление контура. Величина ЭДС индукции – производная магнитного потока по времени и численно равна 0,05 В. Следовательно, сила индукционного тока равна 0,02А.

В результате деформации катушки ее индуктивность уменьшается по закону L= (0,1 – 0,004t) Гн, где t – время в секундах. Найти величину ЭДС самоиндукции, если по катушке течет постоянный ток 70А. (слайд 19).

ЭДС самоиндукции находится по формуле: ЭДС_is = (LI)′. Так как дан закон изменения индуктивности, а сила тока в цепи не меняется, то ЭДС_is = L′I. Находим производную закона изменения индуктивности, умножаем на значение силы тока 70А и получаем ЭДС_is = (0,1 – 0,004t)′ * 70 = 0,28В.

Следующую задачу учащиеся решают на доске и в тетради:

На рисунке показана зависимость от времени силы тока в катушке индуктивностью L=20 мГн. Определите абсолютную величину ЭДС самоиндукции, возникающей в катушке в момент времени t=2,5 секунды. (слайд 20).

По графику определяем, что зависимость I(t) имеет вид I = αt 2 , где коэффициент α = 0,1 А/c 2 . С помощью производной определяем абсолютную величину ЭДС самоиндукции: ЭДС_is = LI′=L*2αt. Вычислим ЭДС_is в момент времени t = 2,5с.

ЭДС_is = 20*10 -3 *2*0,1*2,5 = 0,01В.

Самостоятельная работа

(тест по вариантам из материалов ЕГЭ по физике и математике разных лет).

Тело движется прямолинейно в соответствии с законом X(t) = 2t 3 – 3t, м. Определить значение скорости тела через 2 секунды после начала торможения.

а) 0м/c б) 3,5м/с в) 10 м/с

Уравнение координаты материальной точки имеет вид:

Х = 24 + 10t – t 2 .

Определите время торможения тела.

а) 2c б) 5с в) 0,5с

Под действием силы 150Н тело движется так, что его координата в направлении действия силы изменяется по закону Х = 100 + 5t + 0,5t 2 . Какова масса тела?

а) 12кг б)150г в)0,3кг

Точка движется вдоль оси ОХ, координата ее меняется в соответствии с уравнением Х=(5t 3 – 4t + 8) м, где t- время в секундах. Масса точки равна 2кг. Определите значение ее кинетической энергии через 1с после начала движения.

а) 900Дж б) 11Дж в) 30Дж

В результате изменения сопротивления цепи при помощи реостата сила тока уменьшается по закону I = (300 – 50t) А, где t – время в секундах. Найти величину ЭДС самоиндукции, если индуктивность катушки в цепи составляет 0,04Гн.

а) 0,2В б) 12В в) 2В г) 10В

На рисунке изображены графики зависимости магнитного потока, пронизывающего контур, от времени. Укажите случай, когда ЭДС индукции постоянна.

Тело движется по плоскости, при этом его координаты от времени (в системе СИ) зависят следующим образом: Х(t)=2t 2 +6, y(t)=-1,5t 2 -6. Ускорение тела равно

а) 0м/c 2 б) 3,5м/с 2 в) 0,5м/с 2

Найдите скорость точки, движущейся по закону X(t) = t 2 + 2t + 3, (м) через 3 секунды после начала движения.

а) 2м/c б) 18м/с в) 8 м/с

Уравнение координаты тела имеет вид X = 15 + 3t – 0,5t 2 (величины измерены в системе СИ). Сколько секунд затратило тело на торможение?

а) 3с б) 1с в) 2,5с

На тело массой 300г, движущееся вдоль оси ОХ в соответствии с законом Х(t) = -2t 2 + 5, действует сила, модуль которой равен

а) 0,6Н б) 1,2Н в) 1,5Н

Точка движется вдоль оси ОХ, координата ее меняется в соответствии с уравнением Х = (2t 3 – 4t + 12) м, где t- время в секундах. Масса точки 2кг. Определите значение ее кинетической энергии через 2с после начала движения.

а) 200Дж б) 20Дж в) 400Дж

В результате деформации катушки ее индуктивность уменьшается по закону L= (0,15 – 0,005t) Гн, где t – время в секундах. Найти величину ЭДС самоиндукции, если по катушке течет постоянный ток 70А.

а) 3,5В б) 0,05В в) 1,5В

На рисунке изображены графики зависимости магнитного потока, пронизывающего контур, от времени. Укажите случай, когда ЭДС индукции равна нулю.

Тело движется по плоскости, при этом его координаты от времени (в системе СИ) зависят следующим образом: Х(t)=2t 2 +6, y(t)=-1,5t 2 -6. Ускорение тела равно

а) 0м/c 2 б) 3,5м/с 2 в) 0,5м/с 2 г) 5,0м/с 2 .

Проверка и оценивание ЗУНКов

Учащимся в ходе урока предлагается решить задачи по механике и электродинамике в тетради и сравнить решение и полученный ими ответ с предложенным решением на слайдах презентации.

Рефлексия деятельности на уроке

Дополнительная необходимая информация

В помощь учителю

Использованные источники и литература (если имеются)

Используемая литература.

Обоснование, почему данную тему оптимально изучать с использованием медиа-, мультимедиа, каким образом осуществить

Учащиеся в ходе урока решают задачи в тетради и сравнивают решение и полученный ими ответ с предложенным решением на слайдах презентации. Кроме этого, они после решения заданий теста самостоятельно проверяют его с помощью слайдов презентации. Все это помогает осуществить обратную связь на уроке.

• Для учеников 1-11 классов и дошкольников
• Бесплатные сертификаты учителям и участникам

Областное государственное бюджетное профессиональное образовательное учреждение

МЕТОДИЧЕСКАЯ РАЗРАБОТКА

интегрированного теоретического занятия

физики и математики

Мельникова Мария Николаевна преподаватель математики,

Семёнова Наталья Александровна преподаватель физики

I . Основная часть

1.1. Методическое обоснование темы …………………………………..7-8

1.2. Методические рекомендации по проведению теоретического занятия..9

1.3. План теоретического занятия ……………………………………….10-19

Список использованных источников ……………………………………22-24

Интегрированное занятие, как одна из форм учебного занятия.

Чем же отличается интегрированное занятие от обычного? Сравнительный анализ показывает, что отличие, прежде всего, состоит в специфике учебного материала, на нём рассматриваемого или изучаемого. Чаще всего предметом анализа на таком занятии выступают разноплановые объекты, информация о сущности которых содержится в различных учебных дисциплинах.

Основная часть интегрированного занятия наиболее вариативна, т.к. включает в себя разнообразное содержание изучаемых объектов, которые требуют разных методов обучения и организации познавательной деятельности обучающихся. Интегрированным занятиям присущ значительный потенциал, который реализуется при следующих дидактических условиях:

а) правильное вычисление междисциплинарного объекта изучения, он должен быть актуальным и проблемным, содержать естественную межпредметную связь;

б) тесное сотрудничество преподавателей при подготовке занятия;

в) руководство работой обучающихся, готовящихся выступать на интегрированном занятии;

г) на всех этапах занятия активизация мыслительной деятельности и обязательное использование приёмов обратной связи;

д) обеспечение преемственности между каждой частью занятия на основе общего подхода.

Преподаватель должен хорошо знать психологический климат, возрастные особенности, возможности группы. Это позволит ему решить, какими приемами и методами можно осуществить междисциплинарные связи.

Интеграция – это не смена деятельности и не простое перенесение знаний или действий, которые усвоили обучающиеся, из одной дисциплины в другую для ликвидации утомительных повторных объяснений уже известного или для ускорения процесса обучения, или для закрепления знаний, умений и навыков.

Интеграция – средство интенсификации занятия, высокая форма воплощения междисциплинарных связей на качественно новой ступени. Междисциплинарные связи можно успешно использовать для дополнения, подтверждения или восполнения знаний обучающихся в родственных дисциплинах.

Структура интегрированных занятий требует особой четкости и стройности, продуманности и логической взаимосвязи изучаемого материала по различным дисциплинам на всех этапах изучения. Это успешно достигается за счет компактного, сконцентрированного использования учебного материала программы, а, кроме того, подключения некоторых современных способов организации и изучения учебного материала.

Блок математики

При закреплении или повторении материала обычно активность обучающихся снижается, поэтому необходимо активизировать путем введения инновационных методов.

После проведения всех этапов занятия подсчитываем результаты и выставляем оценки, исходя из количества набранных баллов:

“5” -с 57 до 62 баллов;

“4” – с 50 до 57 баллов;

“3” – с 44 до 50 баллов;

“2” -меньше 44 баллов.

Блок физики

Сегодня на занятии мы будем решать ряд физико-математических задач на вычисление производных и первообразных.

Использование компьютерных технологий в процессе обучения:

1) позволяют повысить положительную мотивацию обучающихся к учению, активизи­рует познавательную деятельность;

2) разви­вает мышление и творческие способнос­ти обучающихся;

3) обеспечивает наглядность протекания физических процессов;

4) формирует активную жизнен­ную позицию в современном и форматизированном обществе.

Знания и умения по решению типовых физико-математических задач: структурировать и систематизировать знания и умения по данной теме;

находить производную, используя правила дифференцирования при решении задач; знать формулы и уравнения физико-математических величин.

Работать в команде, планировать свою деятельность, нести ответственность за результат своей деятельности обучающиеся получают на данном учебном занятии.

В данной методической разработке интегрированного занятия мы хотим продемонстрировать групповую форму организации деятельности обучающихся, использование игровых элементов и элементов технологии проблемного обучения.

I. Основная часть

1.1. Методическое обоснование темы

Теоретическое занятие «Применение производной при

Ведущей целью теоретических занятий является формирование физико-математических умений и навыков, необходимых в последующей профессиональной деятельности. Содержанием теоретических занятий является решение разного рода учебных и профессиональных задач (например, анализ проблемных ситуаций, решение ситуационных производственных и хозяйственных задач).

Наряду с формированием умений и навыков в процессе проведения теоретических занятий обобщаются, систематизируются, углубляются и конкретизируются теоретические знания, вырабатывается способность и готовность использовать теоретические знания в практической деятельности.

Уметь: решать типовые физико-математические задачи; структурировать и систематизировать знания и умения по данной теме

Знать : основы изучения данной темы; определение производной; правила дифференцирования; формулы производных по математике и физике; формулы и уравнения физико-математических величин.

Формируемые компетенции:

Наименование результата обучения

Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес

Организовывать собственную деятельность, исходя из цели и способов её достижения, определённых руководителем

Анализировать рабочую ситуацию, осуществлять текущий и итоговый контроль, оценку и коррекцию собственной деятельности, нести ответственность за результаты своей работы

Использовать информационно – коммуникативные технологии в профессиональной деятельности.

Работать в коллективе и команде, эффективно общаться с коллегами, руководством, клиентами.

1.2. Методические рекомендации по проведению теоретического занятия

На этапе освоения выбранной темы у обучающихся уже имеется представление о производной, правилах дифференцирования, о формулах производных в математике и физике. Поэтому при решении задач мы будем использовать групповую форму работы и элементы технологии проблемного обучения.

Применение групповой формы организации деятельности обучающихся в процессе обучения позволяет формировать у обучающихся навыки:

– умение принять точку зрения другого;

– умение разрешать конфликты;

– умение работать сообща для достижения общей цели.

Применение элементов технологии проблемного обучения подразумевают такую организацию занятий, которая предполагает создание педагогами проблемных ситуаций и активную самостоятельную деятельность обучающихся по их решению, в результате которой происходит творческое овладение профессиональными знаниями, умениями и активное развитие мыслительных способностей. Грамотное использование элементов технологии проблемного обучения приводит к хорошим результатам: повышается мотивация; качество знаний; формируются и развиваются профессиональные компетенции и общие компетенции: умение работать в команде; организовывать собственную деятельность; анализировать рабочую ситуацию, контролировать и корректировать собственную деятельность; осуществлять поиск информации для выполнения поставленных задач.

1.3. План проведения теоретического занятия

План проведения занятия (технологическая карта занятия)

Тип занятия: интегрированный

Актуальность интегрированного занятия

– наглядность и экономия времени за счёт заранее подготовленного материала;

-эффектное и занимательное разнообразие форм занятия;

– зрительное восприятие способствует лучшему усвоению материала и разнообразить занятие.

Цели занятия

– формирование представления о единстве дисциплин в понимании целостности окружающего мира;

-обобщение и систематизация материала полученного на занятиях математики и физики, связанного с производной, механическим движением, колебаниями и волнами в решении задач;

-рефлексия степени усвоения материала.

– ответственное отношение к учебному труду;

-способность работать в группах для достижения цели и нести ответственность за результаты своей работы;

– требовательность к себе и сокурсникам;

– умение выделять главное;

– развивать мышление обучающихся посредством анализа, сравнения и обобщения изученного материала;

-показать необходимость знаний по математике и физике в других науках.

-способствовать развитию познавательной активности;

-развитию мыслительных способностей;

-формированию интереса к учебным дисциплинам;

-навыков контроля и самоконтроля;

-чувства ответственности, самостоятельности, деловые и коммуникативные качества обучающихся.

Формируемые компетенции:

Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.

Организовывать собственную деятельность, исходя из цели и способов её достижения, определённых руководителем.

Анализировать рабочую ситуацию, осуществлять текущий и итоговый контроль, оценку и коррекцию собственной деятельности, нести ответственность за результаты своей работы.

Использовать информационно – коммуникативные технологии в профессиональной деятельности.

Работать в коллективе и команде, эффективно общаться с коллегами, руководством, клиентами.

Средства обучения

Ноутбук, проектор, раздаточный материал, презентация к учебному занятию, оценочный лист на каждого обучающегося.

Обучающейся должен

уметь: решать типовые физико-математические задачи; структурировать и систематизировать знания и умения по данной теме.

знать: основы изучения данной темы; определение производной, правила дифференцирования; формулы производных по математике и физике; основы механики, колебания и волны по физике; формулы и уравнения физико-математических величин.

Планируемый продукт деятельности обучающихся:

1. Умение решать физико-математические задачи по данной теме.

2. Развитие компетенций: ОК1, ОК2, ОК3, ОК4, ОК5, ОК6.

3. Повышение познавательного интереса к интегрированному занятию по данным дисциплинам.

Применение производной в физике на примере физических задач.

Для этого вспомним определение производной Теперь обратимся к курсу физики

Учащиеся рассуждают, вспоминают физические понятия и формулы.

Пусть тело движется по закону S(t)= f(t) Рассмотрим путь, пройденный телом за время от t₀ до t₀+ Δ t, где Δt – приращение аргумента. В момент времени t₀ телом пройден путь S(t₀), в момент t₀+Δt – путь S(t₀ +Δt). Поэтому за время Δt тело прошло путь S(t₀+Δt) –S(t₀), т.е. мы получили приращение функции. Средняя скорость движения тела за этот промежуток времени υ= =

Чем меньше промежуток времени t, тем точнее мы можем узнать, с какой скоростью движется тело в момент t. Устремив t →0, получим мгновенную скорость – числовое значение скорости в момент t этого движения.

υ= , при Δt→0 скорость – есть производная от пути по времени.

Вспомним определение ускорения.

Применяя изложенный выше материал можно сделать вывод, что при t а(t)= υ’(t) ускорение – есть производная от скорости.

Далее на интерактивной доске появляются формулы силы тока, угловой скорости, ЭДС и т.д. Учащиеся дописывают мгновенные значения данных физических величин через понятие производной. (При отсутствии интерактивной доски использовать презентацию)

Вывод формулируют учащиеся.

Вывод: Производная – это есть скорость изменения функции. (Функции пути, координаты, скорости, магнитного потока и т.д.)

Учитель: Мы видим, что связь между количественными характеристиками самых различных процессов исследуемых физикой, техническими науками, химией, аналогична связи между путем и скоростью. Можно привести множество задач, для решения которых также необходимо находить скорость изменения некоторой функции, например: нахождение концентрации раствора в определенный момент, нахождение расхода жидкости, угловой скорости вращения тела, линейной плотности в точке и т.д. Некоторые из таких задач мы сейчас решим.

Закрепление полученных знаний .

Точка движется по закону s(t)=2t³-3t (s – путь в метрах, t – время в секундах). Вычислите скорость движения точки, ее ускорение в момент времени 2с

а(t)=(6t²-3)’=12t
a(2)=12·2=24м/с²
Ответ: υ(2)= 21 м/с; a(2)= 24м/с²

Маховик вращается вокруг оси по закону φ(t)= t 4 -5t. Найдите его угловую скорость ω в момент времени 2с (φ – угол вращения в радианах, ω – угловая скорость рад/с)

φ(t)=t 4 -5t
t=2с
______________
φ(2)=?

ω(t)= φ’(t)
ω(t)=(t 4 -5t)’= 4t³-5
ω(2)=4·2³-5=32-5=27рад/c
Ответ: ω(2)= 27рад/c

Задание3 Тело массой 2 кг движется прямолинейно по закону х(t)=2-3t+2t²

Найдите скорость тела и его кинетическую энергию через 3с после начала движения. Какая сила действует на тело в этот момент времени? (t измеряется в секундах, х – в метрах)

F=ma
a(t)=υ’(t)
a(t)=(-3+4t)’=4м/с
F=2·4=8H
Ответ: υ(3)= 9м/с; E=82 Дж; F=8H

Точка совершает колебательные движения по закону х(t)=2sin3t. Докажите, что ускорение пропорционально координате х.

Читайте также:

  

• Конспект по аппликации в подготовительной группе на тему весна

  

• Химические формулы химия 8 класс конспект рудзитис

  

• План конспект презентация разработка творческого проекта умный дом

  

• Конспект свойства магнита подготовительная группа

  

• Конспект испарение насыщенный и ненасыщенный пар 8 класс презентация

Спецвыпуск

Решение задач с использованием производной

Решение задач с использованием производной

··· Решение задач: примеры, методы,
приёмы ···

А.Н.ДОЛГУШИН,
МОУ СОШ № 23 с УИОП,
г. Воскресенск, Московская обл.

dolgushin23fizika@yandex.ru

Решение задач с использованием
производной

В рамках авторского профильного курса
«Практикум решения физических задач»,
11-й класс.
Базовый уровень

Знать физику – значит уметь решать
задачи.

Э.Ферми

Основными целями и задачами
факультативного курса «Практикум решения
физических задач» являются: знакомство учащихся
с основными типами физических задач: расчётными,
качественными, графическими, исторического
содержания, технического содержания,
межпредметного характера, комбинированными,
задачами-оценками; формирование знаний, умений и
навыков решения физических задач, в том числе
повышенной сложности; ознакомление с разными
способами решения физических задач: логическим,
математическим (арифметическим, алгебраическим,
графическим, геометрическим) и
экспериментальным; разбор типовых заданий на
вступительных экзаменах в технические вузы (МЭИ,
МГТУ им. Н.Э.Баумана).

Подборка задач соответствует основным
темам школьного курса физики, где можно
использовать элемент математического анализа –
производную:

– «Кинематика»: если изменение
координаты задано уравнением вида x = x(t),
то производная первого порядка от координаты по
времени есть скорость, т.е. (t) = x‘(t), а производная
второго порядка от координаты по времени, или
производная первого порядка от скорости по
времени, есть ускорение, т.е. a(t) = x“(t)
= ‘ (t);

– «Импульс»: при определении импульса
по формуле p = m он определяется по скорости тела как
производной от координаты по времени.

– «Механические колебания»:
энергетический подход (метод производной)
позволяет вывести дифференциальные уравнения
второго порядка, описывающие процессы в
математическом и пружинном маятниках, затем
получить формулы для периодов колебаний, а также
рассчитать период колебаний сложных
колебательных систем;

– «Термодинамика»: использование
производной позволяет решать задачи на
нахождение экстремальных значений параметров в
циклах идеального газа;

– «Электромагнитная индукция»:
производная от магнитного потока по времени,
взятая с противоположным знаком (по правилу
Ленца), позволяет определить мгновенное значение
ЭДС, индуцируемой в замкнутом проводящем
контуре: _i
= –Ф‘ (t);

– «Постоянный ток»: производная
позволяет определить величину внешнего
сопротивления в цепи постоянного тока, при
которой полезная мощность принимает
максимальное значение;

– «Электромагнитные колебания»:
энергетический подход (метод производной)
позволяет вывести дифференциальное уравнение
второго порядка, описывающее процессы в
идеальном колебательном контуре, а затем
получить формулу Томсона;

– «Цепи переменного тока»:
производная позволяет установить разность фаз
между колебаниями электрического заряда на
обкладках конденсатора и силы тока в цепи с
ёмкостным сопротивлением;

– «Геометрическая оптика»: используя
принцип Ферма, можно вывести закон преломления
света.

Рассмотрим некоторые задачи.

Кинематика. Закон сохранения энергии

• [1]. Движение материальной точки
описывается уравнениями: x = 10 cos 3t, y
=10 sin 3t. [x] = см, [y] = см, [] = c^–1.
Определите скорость, ускорение и траекторию
точки.

Решение

– Скорость: ² = _x² + _y². Используя
механический смысл производной, после
преобразований получаем = 30 см/с.

– Ускорение: a² = a_x²
+ a_y². Используя механический смысл
производной, после преобразований получаем a =
90 см/с².

– Траектория: уравнение
траектории движущейся точки определяется
зависимостью: y = f(x), т.е. позволяет
исключить переменную t. Целесообразно обе
части исходных уравнений движения материальной
точки возвести в квадрат, а затем сложить.
Используя основное тригонометрическое
тождество cos² + sin²
= 1, после преобразований получаем x² + y²
= 100, что соответствует уравнению окружности
радиусом 10 см с центром в точке с координатами (0;
0).

• [2]. Небольшое тело соскальзывает
без начальной скорости с вершины гладкой горки
высотой H, имеющей горизонтальный трамплин
высотой h. При какой высоте h тело пролетит
наибольшее расстояние s по горизонтали? Чему
равно это расстояние?

Решение

Связываем нулевой уровень с
поверхностью Земли, используем закон сохранения
механической энергии: mgH = mgh + m²/2. С момента
отрыва тела от трамплина используем
кинематические уравнения движения тела,
брошенного горизонтально:

h = gt²/2 – по вертикали;

= s/t
– по горизонтали, т.к. g_x = 0.

Время падения по вертикали совпадает со
временем движения тела по горизонтали. В итоге
получаем выражение для скорости в момент отрыва
тела от трамплина: – которое подставляем в выражение
для закона сохранения энергии. После
преобразования получаем зависимость

Далее исследуем полученную
зависимость, находим производную по переменной h
и приравниваем её к нулю (s‘_h = 0):

т.е. расстояние s будет наибольшим
при h = H/2, когда производная обращается в нуль:
4H – 8h = 0.

Подставляя полученное выражение для
высоты трамплина h = H/2 в формулу для s,
получаем s = H.

Импульс

• [3]. Движение материальной точки в
единицах СИ описывается уравнением x = 5 – 8t +
4t². Приняв массу точки равной 2 кг,
найдите её импульс через 2 с и через 4 с от начала
отсчёта времени, а также силу, вызвавшую это
изменение импульса.

Решение

Уравнение скорости с учётом
механического смысла производной имеет вид: = –8 + 8t. Тогда
импульс через 2 с от начала отсчёта времени: p₂
= 16 кг · м/с, а импульс через 4 с: p₄ = 48 кг ·
м/с.

Сила, которая вызывает это изменение
импульса, определяется с учётом второго закона
Ньютона в импульсной форме: F = (p₄ – p₂)/t, где t = 2 с. Численно
получаем: F = 16 Н.

Механические колебания

• [1]. Материальная точка массой m движется
вдоль оси X по закону x = A sint, где A, – некоторые постоянные, t
– время. Определите модуль изменения импульса
материальной точки с момента времени t = t₁
до момента времени t = t₂.

Решение

По механическому смыслу производной
скорость определяется выражением: =Acost. Тогда модуль изменения импульса
определяется выражением:

p = mA|cost₂ – cost₁|.

• [ЕГЭ]. Тело, подвешенное на
пружине, совершает свободные гармонические
колебания частотой . С какой частотой происходит изменение
кинетической энергии тела?

Решение

Пусть координата тела изменяется по
закону x = x₀sint. Используя механический смысл
производной, находим закон изменения скорости: = x‘ = x₀cost. Тогда
кинетическая энергия тела W_k = m²/2 = (mx₀²²cos²t)/2. С учётом
тригонометрического тождества cos²t = (1 +
+ cos2t)/2,
получаем: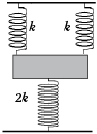

W_k = mx₀²²(1 + cos2t)/4,

следовательно, изменение кинетической
энергии колеблющегося тела происходит с
частотой 2.

• [2]. Брусок подвешен за края к
потолку на двух одинаковых пружинах жёсткостью k
каждая и притянут к полу пружиной жёсткостью 2k.
Масса бруска m. Определите период колебаний
бруска.

Решение

Важно отметить, что сила тяжести,
действующая на брусок, постоянна, поэтому на
период колебаний не влияет. Для доказательства
рассмотрим груз, подвешенный на вертикальной
пружине. В положении равновесия справедливо
равенство: mg = kx₀. В процессе колебаний,
для произвольного момента времени (например, при
дополнительном растяжении на величину x)
второй закон Ньютона в скалярной форме имеет вид:
–k(x₀ + x) + mg = mx“.

После преобразований получаем
уравнение, в котором исключена сила тяжести: –kx
= mx“. Далее приходим к
дифференциальному уравнению второго порядка,
описывающему колебания пружинного маятника с
вертикальной пружиной:

Полученный результат показывает, что
постоянная сила тяжести не влияет на период
колебаний.

С учётом закона сохранения
механической энергии в любой момент времени W_k
+ W_упр = const, т.е.

Далее находим производную от обеих
частей:

Термодинамика. Газовые законы

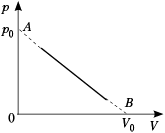
• [4]. Состояния идеального газа в
количестве =
1 моль в ходе некоторого процесса изображаются
точками, лежащими на отрезке прямой AB: V_A =
0, p_A = p₀; V_B = V₀, p_B
= 0. Найдите зависимость температуры газа от
объёма и определите максимальную температуру
газа в ходе такого процесса.

Решение

В соответствии с графиком составляем
уравнение прямой: y = –kx + b, где y = p, x = V, b =
p₀;

Заменяя переменные, получаем:

Зная уравнения Клапейрона–Менделеева
pV = RT, находим
зависимость температуры идеального газа от
объёма:

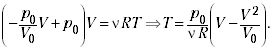
Находим производную и приравниваем её
нулю:

Решая последнее уравнение, получаем,
что температура максимальна при V = V₀/2.
Подставляя это значение в выражение для
температуры, после преобразований получаем

Электромагнитная индукция

• [2]. Проводящий контур площадью S
= 400 см², в который включён конденсатор
ёмкостью C = 10 мкФ, расположен в однородном
магнитном поле перпендикулярно линиям индукции.
Магнитная индукция возрастает по закону
B = (2 + 5t)10^–2 Тл, где t – время в
секундах. Определите энергию электрического
поля конденсатора. Укажите, какая обкладка
конденсатора заряжается положительно.

Решение

Изменение магнитной индукции приводит
к появлению в цепи электрического тока (между
обкладками конденсатора – диэлектрик),
конденсатор начнёт заряжаться, следовательно,
между его обкладками возникнет электрическое
поле энергией W = CU²/2 = C_i²/2, где
_i = –Ф_t‘
= –(BScos)_t‘
– ЭДС, наводимая между обкладками
конденсатора. Площадь контура постоянна, = B^n =
0° (по условию),
cos 0° = 1, поэтому:

_i =
–S · B_t‘ = –4 · 10^–2 · 5 · 10^–2
= –2 · 10^–3 (В).

Подставляя найденное значение в
выражение для энергии электрического поля
заряженного конденсатора, получаем W = 20 ·
10^–12 Дж.

Чтобы определить, какая из обкладок
конденсатора зарядится положительно, используем
правило Ленца: т.к., по условию задачи, величина
магнитной индукции увеличивается, то вектор
магнитной индукции внешнего магнитного поля B
направлен противоположно вектору магнитной
индукции магнитного поля B_i
наведённого в контуре тока. Зная направление B_i
и правило правой руки (правого винта), определяем
направление индукционного тока: против часовой
стрелки. Поскольку за направление
электрического тока принимают упорядоченное
движение положительно заряженных частиц, то
приходим к выводу, что нижняя обкладка
конденсатора заряжается положительно.

• [5]. Рамка площадью S = 100 см²
расположена перпендикулярно однородному
магнитному полю, индукция которого изменяется по
закону B = ct³ – at², где c = 1
Тл/с², t – время в секундах, a = 3 Тл/с³.
Сопротивление рамки R = 10^–2 Ом. В какой
момент времени индукционный ток максимален? Чему
он равен?

Решение

Найдём зависимость индукционного тока
от времени: I_i = _i/R, где _i = –Ф_t‘
= –(BScos)_t‘
= –SB_t‘ = –S(ct³ – at²)_t‘
= –S(3ct² – 2at), т.е.
I_i = –S(3ct² – 2at)/R.

Исследуем полученную зависимость, т.е.
найдём производную и приравняем её нулю:

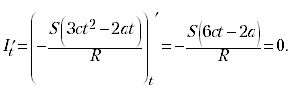
При индукционный
ток принимает максимальное значение:

Находим числовые значения: t = 1 с, I_i
max = 3 А.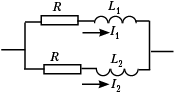

• [3]. В цепи, представленной на
рисунке, L₁ = 0,02 Гн, L₂ = 0,01 Гн.
Силы токов изменяются во времени по законам: I₁
= 0,2 + 10t, I₂ = 0,1 + 10t. Найдите
сопротивление R. Величины токов заданы в СИ.

Решение

При параллельном соединении участков
цепи:

Следовательно:

Геометрическая оптика

• [1]. На каком расстоянии d_min
надо поместить предмет от собирающей линзы с
фокусным расстоянием F, чтобы расстояние от
предмета до его действительного изображения
было наименьшим?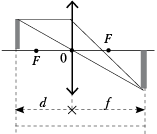

Решение

Выполним рисунок. Используем формулу
тонкой линзы с учётом правила знаков: из которой выразим
расстояние от оптического центра собирающей
линзы до предмета:

Расстояние от предмета до его действительного
изображения
Исследуем последнее выражение, для чего найдём
производную от s по d и приравняем её нулю:

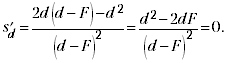
Из равенства d² – 2dF = 0
следует d_min = 2F. При этом значении d
расстояние от предмета до его действительного
изображения будет наименьшим: s_min = 4 F.

Литература

1. Дмитриев С.Н., Васюков В.И., Струков
Ю.А. Физика. Сборник задач для поступающих в
вузы: Изд. 5-е, доп. – М.: Демиург-Арт, 2001.

2. Славов А.В., Спивак В.С., Цуканов
В.В. Сборник задач по физике: Учеб. пособие для
довуз. подгот.: Под ред. А.В.Славова: Изд 7-е, испр. и
доп. – М.: Издательство МЭИ, 2006.

3. Рымкевич А.П. Физика. Задачник.
10–11 кл. – М.: Дрофа, 2006.

4. Баканина Л.П., Белонучкин В.Е., Козел
С.М. Сборник задач по физике для 10–11 классов с
угл. изучением физики: Под ред. С.М.Козела. – М.:
Вербум, 2003.

5. Турчина Н.В. Физика: 3800 задач для
школьников и поступающих в вузы. – М.: Дрофа, 2000.

Ещё два примера решения задач с помощью
производной приведены в рубрике «Дополнительные
материалы» к № 12 на сайте газеты http://fiz.1september.ru

Магнитный поток и ЭДС индукции

Продолжаем решать задачи на магнитный поток и ЭДС индукции. Здесь уже будет потяжелее: придется и производную, и первообразную находить. Но задачи интересные, и даже геометрические знания пригодились, а именно, формула площади треугольника.

Задача 1.

Плоский замкнутый металлический контур площадью см, находится в однородном магнитном поле, индукция которого Тл. Площадь контура за время c равномерно уменьшается до см (плоскость контура при этом остается перпендикулярной магнитному полю). Определите силу тока (в мкА), протекающего по контуру в течение времени , если сопротивление контура Ом.

Поток уменьшился с до , его изменение . Следовательно,

Ток равен

Ответ: 16 мкА

Задача 2.

Медное кольцо радиусом см из проволоки диаметром мм  расположено в однородном магнитном поле, изменяющемся со скоростью Тл/с. Плоскость кольца перпендикулярна силовым линиям магнитного поля. Определите силу индукционного тока, возникающего в кольце. Удельное сопротивление меди равно Ом м.

Сопротивление кольца равно

Ток в кольце будет равен

Ответ: 0,693 А

Задача 3.

При изменении силы тока в замкнутом контуре индуктивностью Гн  ЭДС самоиндукции изменялась согласно графику (см. рис.). Чему равна величина изменения тока в интервале времени 1-4 с?

Так как

То, чтобы найти ток, нужно найти интеграл. То есть – определить площадь под графиком с первой по 4 секунду. Площадь будет равна сумме площадей трапеции и прямоугольника: 3+8.

Ответ: 0,11 А

Задача 4.

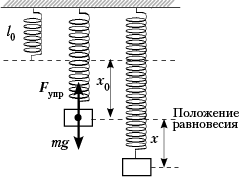
В однородном магнитном поле с индукцией В = 0,2 Тл начинает двигаться металлический стержень длиной см перпендикулярно вектору магнитной индукции. Координата стержня изменяется по закону . Какая разность потенциалов возникает между концами стержня через 5 с?

Скорость стержня к указанному моменту времени будет равна:

Следовательно, ЭДС:

Ответ: 0,68 В.

Задача 5.

Проводящий квадратный контур со стороной см, помещенный в однородное магнитное поле с индукцией В = 0,5 Тл, вектор которой перпендикулярен плоскости контура, складывают пополам (см. рис.). Какой заряд протечет по контуру, если сопротивление единицы длины контура равно  Ом/м?

Площадь контура, складывая его, уменьшают до нуля. Поэтому изменение потока равно . Следовательно,

Откуда

Ответ: 0,125 Кл.

Задача 6.

Напряжение на зажимах рамки, начинающей вращаться в однородном магнитном поле, изменяется с течением времени согласно графику на рисунке. Чему приблизительно равна величина магнитного потока, пересекающего рамку в момент времени с?

Напряжение на зажимах, или ЭДС, есть производная потока, поэтому поток – первообразная ЭДС. ЭДС, судя по графику, можно записать так:

Период равен 4 с, тогда . Амплитуда ЭДС равна 40 мВ, следовательно,

Определяем первообразную, то есть берем интеграл:

Подставим нужное время:

Ответ: 18 мВб.

Задача 7.

Плоская проволочная рамка находится в магнитном поле, его плоскость перпендикулярна линиям индукции. При равномерном уменьшении магнитного поля до нуля за время с в рамке возник постоянный ток А. Какой ток потечет по рамке при ее повороте в этом поле с постоянной угловой скоростью на угол за время с вокруг оси, перпендикулярной вектору В и лежащей в плоскости рамки?

И в том, и в другом случае меняется поток через рамку. Но индукция поля остается неизменной, ее–то и надо найти:

Откуда

Если рамку повернуть, то изменится площадь, пронизываемая потоком:

Тогда

Подставим индукцию, найденную ранее:

Ответ: 6 мА.

Задача 8.

Квадратная рамка со стороной см помещена в однородное магнитное поле с индукцией мТл так, что линии индукции перпендикулярны плоскости рамки (см. рис.). Сопротивление рамки 1 Ом. Какое количество тепла выделится в рамке за 10 с, если ее выдвигать из области, в которой создано поле со скоростью 1 см/с, перпендикулярной линиям индукции? Поле сосредоточено в некоторой четко ограниченной области.

Площадь рамки, помещенная в поле, будет изменяться. Поэтому поток меняется и в рамке наводится ЭДС.

Ток будет равен:

При протекании такого тока выделится количество теплоты

Ответ: 0,8 нДж

Задача 9.

Квадратная рамка помещена в однородное магнитное поле. Нормаль к плоскости рамки составляет с направлением магнитного поля угол . Сторона рамки см. Известно, что среднее значение ЭДС индукции, возникающей в рамке при выключении поля в течение времени с, равно 50 мВ. С какой силой подействовало бы это магнитное поле на протон, влетевший в него со скоростью м/с перпендикулярно вектору ?

. Следовательно,

Пронизываемая потоком площадь рамки равна

Тогда

Найдем из этого выражения индукцию поля:

Сила Лоренца равна

Ответ: Н.

Задача 10.

Рамка сопротивлением 15 Ом, имеющая форму равностороннего треугольника, помещена  в однородное магнитное поле с индукцией Тл. Плоскость рамки составляет с направлением вектора угол . Определите длину стороны рамки , если при равномерном уменьшении индукции В до нуля в течение с в проводнике рамки выделяется количество тепла 0,5 мДж.

По закону Джоуля-Ленца

Откуда

По закону Ома ,

Площадь рамки равна , площадь, пронизываемая потоком, равна

Тогда

Откуда

Ответ:  м.