Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте
его в существующую тему, а создайте новую в корневом разделе “Помогите решить/разобраться (М)”.
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву
, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения
и указать конкретные затруднения.
Обязательно просмотрите тему
Правила данного раздела, иначе Ваша тема может быть удалена
или перемещена в Карантин, а Вы так и не узнаете, почему.
|
|
Синус трети угла
|
|
14/10/06 |
Помогите! (наподобие синуса половинного угла). В справочниках найти не удалось. Спасибо!
|
|
|
|
|
Brukvalub |
|
||
01/03/06 |
Дело в том, что известная формула
|
||
|
|
|||
|
незваный гость |
|
||
17/10/05 |
|
||
|
|
|||
|
SergeiMS |
|
|
18/10/06 |
Эта задача просто эквивалентна решению произвольного кубического уравнения.
|
|
|
|
|
ГЕС |
|
|
14/10/06 |
господа, то, что надо решать кубическое ур-ие (по формуле Кардано) я знаю, но беда в том, что решить его не могу, поэтому и решил обратиться в форум за помощью.
|
|
|
|
|
worm2 |
|
||
01/08/06 |
Правильно! Оно и не выражается в общем случае через радикалы от вещественных чисел, если у уравнения 3 вещественных корня. Это — так называемый неприводимый случай (casus irreducibilis), который и имел в виду незваный гость . Как раз в этом случае решение приходится выражать через тригонометрические (и обратные к ним) функции.
|
||
|
|
|||
|
EsenZhar |
|
|
07/10/06 |
Можно решить кубическое уравнение относительно sin трети угла с Добавлено спустя 2 минуты 26 секунд: Формулы решения куб. уравнений есть в справочниках.
|
|
|
|
|
RIP |
|
||
11/01/06 |
EsenZhar , Вы бы прочитали, что писали до Вас.
|
||
|
|
|||
|
Sasha2 |
|
|
21/06/06 |
Вообще при помощи этой формулы можно получить какие-нибудь содержательные результаты? Например, можно ли как нибудь получить значение tan(10o)?
|
|
|
|
|
Macavity |
|
||
05/09/05 |
Вероятно, отсутствие формулы связано с неразрешимостью трисекции угла. Или нет?
|
||
|
|
|||
|
ИСН |
|
||
18/05/06 |
Формула есть, вот она передо мной, но сюда писать я её не хочу, очень уж много букв. Получить выражение для тангенса десяти градусов – можно, но будет оно таким громоздким, что это примерно то же самое, что и… не получать.
|
||
|
|
|||
|
Руст |
|
||
09/02/06 |
Macavity писал(а): Вероятно, отсутствие формулы связано с неразрешимостью трисекции угла. Или нет? Не из-за отсутствия формулы эта задача с помощью циркуля и линейки неразрешима. Несложно доказать, что с помощью циркуля и линейки можно получить только числа, выражаемые квадратичными расширениями поля Q. Для решения общего уравнения третьей степени (хотя оно и разрешимо в радикалах, т.е. Группа Галуа разрешимая группа), приходится пользоваться кубическими корнями, чего нельзя добиться циркулем и линейкой. В частности, в задаче построения правильного n угольника, разрешимость имеет место тогда и только тогда, когда максимальный нечётный делитель n представляется в виде произведения различных простых чисел Ферма. Пока известно только 5 простых числа Ферма 3,5,17,257,65537 (и есть соображения, что других нет), соответственно циркулем и линейкой можно построить только 32 правильных многоугольника с нечётным числом сторон.
|
||
|
|
|||
|
ИСН |
|
||
18/05/06 |
2Руст : в эти 32 Вы включили моноугольник?
|
||
|
|
|||
|
Руст |
|
||
09/02/06 |
Да, спасибо, за поправку, включил одноугольник.
|
||
|
|
|||
|
Trueman |
|
|
06/11/05 |
почему бы не получить, например, так формулу Добавлено спустя 2 часа 34 минуты 53 секунды: а извиняюсь, я условие чётко не уяснил, думал просто связь установить
|
|
|
|
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Есть треугольник. Известны синусы двух углов (не табличные значения), больше ничего не дано. Как найти синус третьего угла?
Ученик
(218),
на голосовании
7 лет назад
Голосование за лучший ответ
Павел Бояркин
Мастер
(2231)
7 лет назад
По таблице Брадиса можно определить углы через синусы, а так как сумма углов в треугольнике 180 градусов, можно без проблем найти и третий угол (а соответственно, через него и синус).
***fillskii@mail.ru
Просветленный
(28638)
7 лет назад
Дано: sin(A)=a; sin(B)=b найти: sin(C)=
С=180-А-В
sin(C)=sin(180-A-B)=sin(180-(A+B))=sin(A+B)=sin(A)*cos(B)+cos(A)*sin(B)
Теперь cos(B)=sqrt(1-(sin(B))^2)=sqrt(1-b^2)
cos(A)=sqrt(1-(sin(A))^2)=sqrt(1-a^2)
Получаем: sin(C)=a*sqrt(1-b^2)+b*sqrt(1-a^2) при условии, что А и В – острые
Синус тройного угла
ОПРЕДЕЛЕНИЕ
Синус тройного угла выражается через синус этого угла следующим образом
(
sin 3 alpha=3 sin alpha-4 sin ^{3} alpha
)
Примеры решения задач
ПРИМЕР 1
Найти значение (
sin 3 alpha
) , (
operatorname{ctg} alpha=2
), (
0<alpha<frac{pi}{2}
)
Пользуясь основными тригонометрическими тождествами выразим синус через котангенс
(
sin ^{2} alpha=frac{1}{1+operatorname{ctg}^{2} alpha}=frac{1}{1+4}=frac{1}{5}
)
(
sin alpha=frac{1}{sqrt{5}}
)
Подставим полученное значение в формулу синуса тройного угла
(
sin 3 alpha=3 sin alpha-4 sin ^{3} alpha=frac{3}{sqrt{5}}-frac{4}{5 sqrt{5}}=frac{11}{5 sqrt{5}}=frac{11 sqrt{5}}{25}
)
Ответ:
(
sin 3 alpha=frac{11 sqrt{5}}{25}
)
ПРИМЕР 2
Упростить выражение
(
frac{sin 3 alpha+sin alpha}{4 cos ^{2} alpha}
)
Используя формулу синуса тройного угла, преобразуем выражение
(
frac{sin 3 alpha+sin alpha}{4 cos ^{2} alpha}=frac{3 sin alpha-4 sin ^{3} alpha+sin alpha}{4 cos ^{2} alpha}=frac{4 sin alpha-4 sin ^{3} alpha}{4 cos ^{2} alpha}=frac{4 sin alphaleft(1-sin ^{2} alpharight)}{4 cos ^{2} alpha}=frac{4 sin alpha cos ^{2} alpha}{4 cos ^{2} alpha}=sin alpha
)
(
frac{sin 3 alpha+sin alpha}{4 cos ^{2} alpha}=sin alpha
)
Как найти синус угла в треугольнике? Не в прямоугольном, в любом
Если рассматриваемый треугольник является прямоугольным, то можно использовать базовое определение тригонометрической функции синуса для острых углов. По определению синусом угла называют соотношение длины катета, лежащего напротив этого угла, к длине гипотенузы этого треугольника. То есть, если катеты имеют длину А и В, а длина гипотенузы равна С, то синус угла α, лежащего напротив катета А, определяйте по формуле α=А/С, а синус угла β, лежащего напротив катета В – по формуле β=В/С. Синус третьего угла в прямоугольном треугольнике находить нет необходимости, так как угол, лежащий напротив гипотенузы всегда равен 90°, а его синус всегда равен единице.
2
Для нахождения синусов углов в произвольном треугольнике, как это ни странно, проще использовать не теорему синусов, а теорему косинусов. Она гласит, что возведенная в квадрат длина любой стороны равна сумме квадратов длин двух других сторон без удвоенного произведения этих длин на косинус угла между ними: А²=В²+С2-2*В*С*cos(α). Из этой теоремы можно вывести формулу для нахождения косинуса: cos(α)=(В²+С²-А²)/(2*В*С) . А поскольку сумма квадратов синуса и косинуса одного и того же угла всегда равна единице, то можно вывести и формулу для нахождения синуса угла α: sin(α)=√(1-(cos(α))²)= √(1-(В²+С²-А²)²/(2*В*С) ²).
3
Воспользуйтесь для нахождения синуса угла двумя разными формулами расчета площади треугольника, в одной из которых задействованы только длины его сторон, а в другой – длины двух сторон и синус угла между ними. Так как результаты их будут равны, то из тождества можно выразить синус угла. Формула нахождения площади через длины сторон (формула Герона) выглядит так: S=¼*√((А+В+С) *(В+С-А) *(А+С-В) *(А+В-С)) . А вторую формулу можно написать так: S=А*В*sin(γ). Подставьте первую формулу во вторую и составьте формулу для синуса угла, лежащего напротив стороны С: sin(γ)= ¼*√((А+В+С) *(В+С-А) *(А+С-В) *(А+В-С) /(А*В)) . Синусы двух других углов можно найти по аналогичным формулам.
Синус угла в обычном треугольнике
Синус (sin) – это одна из прямых тригонометрических функций. Подробнее о ней можно узнать из нашей статьи Что такое синус.
Синус угла в прямоугольном треугольнике
Прежде чем выяснять, как найти синус угла, необходимо определиться с условными обозначениями. Пусть в прямоугольном треугольнике:
- α – острый угол, синус которого нужно найти;
- с – гипотенуза;
- b – прилежащий катет;
- a – противолежащий катет.
Тогда чтобы найти синус острого угла прямоугольного треугольника, достаточно посчитать соотношение длины противолежащего катета к длине гипотенузы: sin(α) = a/c. При этом стоит запомнить, что sin 90° всегда равен 1.
Синус угла в произвольном треугольнике
Находить синус угла в произвольном треугольнике проще всего с использованием теоремы косинусов (cos): квадрат длины любой стороны равен сумме квадратов длин двух других сторон за минусом их удвоенного произведения на косинус угла между ними.
a² = b² + c² – 2*b*c*cos(α)
Из данной формулы можно найти косинус: cos(α) = (b² + c² – a²)/(2*b*c)
А поскольку для одного и того же угла sin(α)² + cos(α)² = 1 и это константа, то можно вывести формулу для определения синуса:
Более детально нахождение синуса угла с использованием косинуса рассмотрено в нашей статье Как найти синус, если известен косинус.
Что такое синус в треугольнике? Как найти синус острого угла в прямоугольном треугольнике?
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
для угла A треугольника ABC
противолежащий катет — это BC.
Соответственно, синус угла A в треугольнике ABC — это
Для угла B треугольника ABC
противолежащим является катет AC.
Соответственно, синус угла B в треугольнике ABC
равен отношению AC к AB:
Таким образом, синус острого угла в прямоугольном треугольнике — это некоторое число, получаемое в результате деления длины противолежащего катета на длину гипотенузы. Длины отрезков выражаются положительными числами, поэтому синус угла треугольника также является положительным числом.
Поскольку длина катета всегда меньше длины гипотенузы, то синус острого угла прямоугольного треугольника — число, меньшее единицы.
Синус любого острого угла прямоугольного треугольника больше нуля, но меньше единицы:
Синус угла треугольника зависит не от длин сторон треугольника, а от отношения этих длин.
1) В треугольнике ABC катет BC=3 см, а гипотенуза AB=5 см.
2) В треугольнике ABC катет BC=21 дм, гипотенуза AB=35 дм.
Длины сторон треугольника изменилось, но отношения длин остались прежними, поэтому и значение синуса угла A не изменилось.
2
Для нахождения синусов углов в произвольном треугольнике, как это ни странно, проще использовать не теорему синусов, а теорему косинусов. Она гласит, что возведенная в квадрат длина любой стороны равна сумме квадратов длин двух других сторон без удвоенного произведения этих длин на косинус угла между ними: А²=В²+С2-2*В*С*cos(α). Из этой теоремы можно вывести формулу для нахождения косинуса: cos(α)=(В²+С²-А²)/(2*В*С) . А поскольку сумма квадратов синуса и косинуса одного и того же угла всегда равна единице, то можно вывести и формулу для нахождения синуса угла α: sin(α)=√(1-(cos(α))²)= √(1-(В²+С²-А²)²/(2*В*С) ²).
Тригонометрия простыми словами
Официальное объяснение тригонометрии вы можете почитать в учебниках или на других интернет сайтах, а в этой статье мы хотим объяснить суть тригонометрии “на пальцах”.
Тригонометрические функции связаны с соотношениями сторон в прямоугольном треугольнике:
- Синус угла – отношение противолежащего катета к гипотенузе;
- Косинус угла – отношение прилежащего катета к гипотенузе;
- Тангенс угла – отношение противолежащего катета к прилежащему;
- Котангенс угла – отношение прилежащего катета к противолежащему.
Или в виде формул:
Для удобства работы с тригонометрическими функциями был придуман тригонометрический круг, который представляет собой окружность с единичным радиусом (r = 1).
Тогда проекции радиуса на оси X и Y (OB и OA’) равны катетам построенного треугольника ОАВ, которые в свою очередь равны значениям синуса и косинуса данного угла.
Тангенс и котангенс получаются соответстсвенно из треугольников OCD и OC’D’, построенных подобно исходному треугольнику OAB.
Для упрощения обучения тригонометрическим функциям в школе используют только некоторые удобные углы в 0°, 30°, 45°, 60° и 90°.
Значения тригонометрических функций повторяются каждые 90° и в некоторых случаях меняя знак на отрицательный.
Достаточно запомнить значения некоторых важных углов и понять принцип повтора значений для бОльших углов.
Значения тригонометрических функций
для первой четверти круга (0° – 90°)
| 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|
| sin | 0 | 1 | √3 | – |
| ctg | – | √3 | 1 |
Принцип повтора знаков тригонометрических функцийУгол может быть как положительный, так и отрицательный. Отрицательный угол считается угол, откладываемый в противоположную сторону. В виду того, что полная окружность составляет 360°, значения тригонометрических функций углов, описывающих одинаковое положение радиуса, РАВНЫ. Например, значения тригонометрических функций для углов 270° и -90° равны. Для лучшего понимания и запоминания значений тригонометрических функций воспользуйтесь динамическим макетом тригонометрического круга ниже. Нажимая кнопки «+» и «–» значения угла будут увеличиваться или уменьшаться соответственно. Тригонометрический кругУглы в радианахДля математических вычислений тригонометрических функций используются углы не в градусах, а в радианах. Что такое радиан? Угол в радианах равен отношению длины дуги окружности к радиусу. Полный круг в 360° соответствует длине окружности 2 π r. Следовательно 360° в радианах равно 2 π , а 180° равно π радиан. Как преобразовывать градусы в радианы? Нужно значение в градусах разделить на 180° и умножить на π . Чтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций. [spoiler title=”источники:”] http://dudom.ru/kompjutery/sinus-ugla-v-obychnom-treugolnike/ http://matematika.club/articles/trigonometry/ [/spoiler] |
Формулы (тождества) синус, косинус, тангенс, котангенс тройного угла
Формулы преобразования функций (синус, косинус, тангенс, котангенс), тройного угла (3α) в выражение через одинарный угол (α):
sin тройного угла

cos тройного угла

tg тройного угла
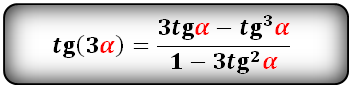
ctg тройного угла
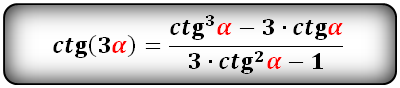
- Подробности
-
Автор: Administrator
-
Опубликовано: 17 сентября 2011
-
Обновлено: 13 августа 2021
 показывает, что для получения желаемой Вами формулы требуется решить кубическое уравнение, что не так просто, как решение соответствующего квадратного уравнения для вычисления синуса половинного угла. Поэтому в справочнике и нет нужной Вам формулы.
показывает, что для получения желаемой Вами формулы требуется решить кубическое уравнение, что не так просто, как решение соответствующего квадратного уравнения для вычисления синуса половинного угла. Поэтому в справочнике и нет нужной Вам формулы.

