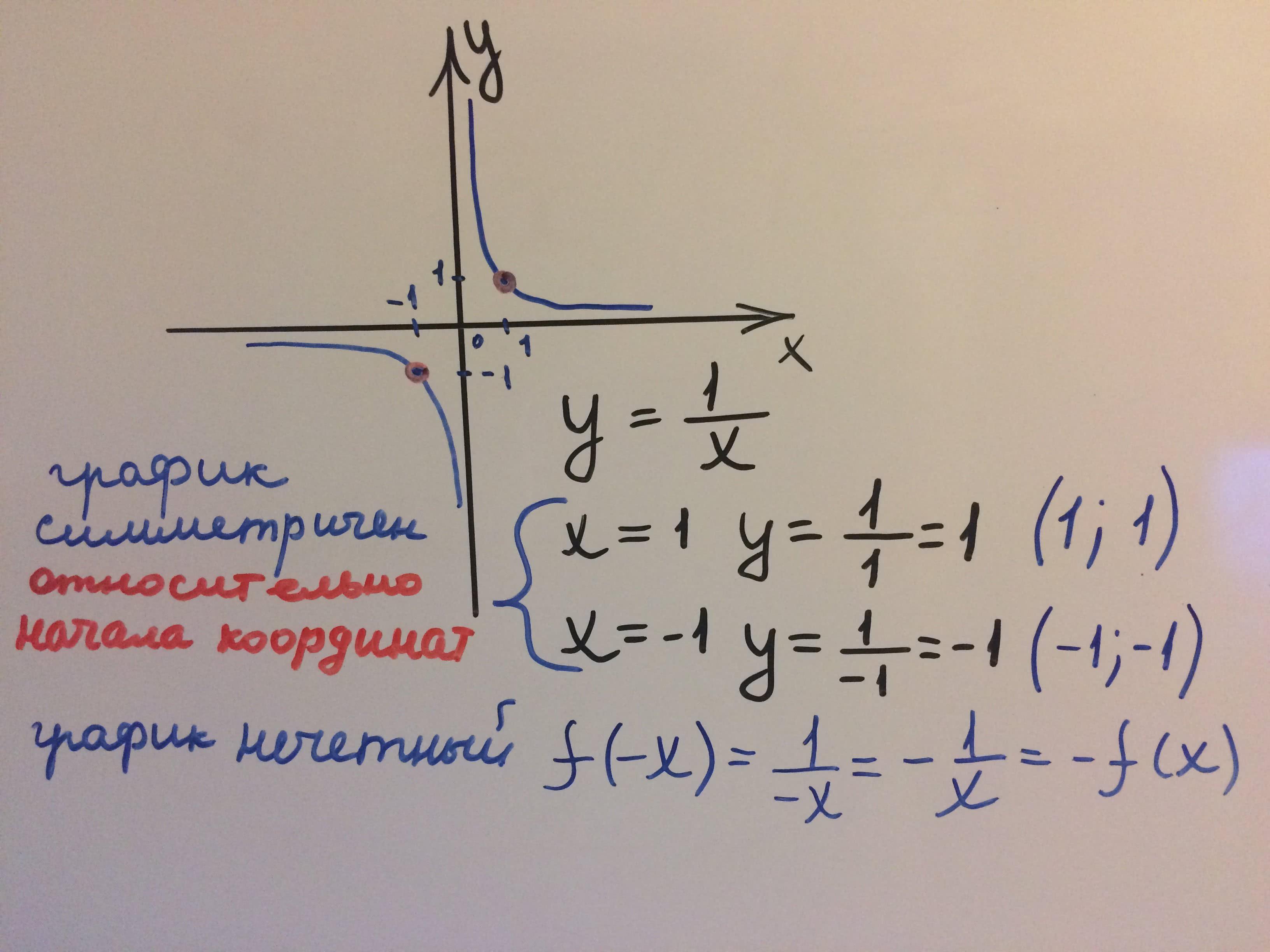
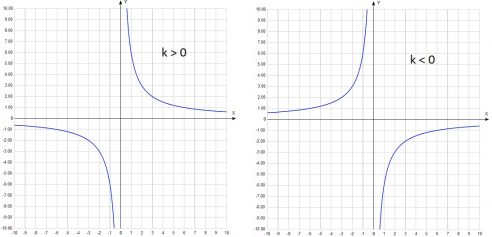
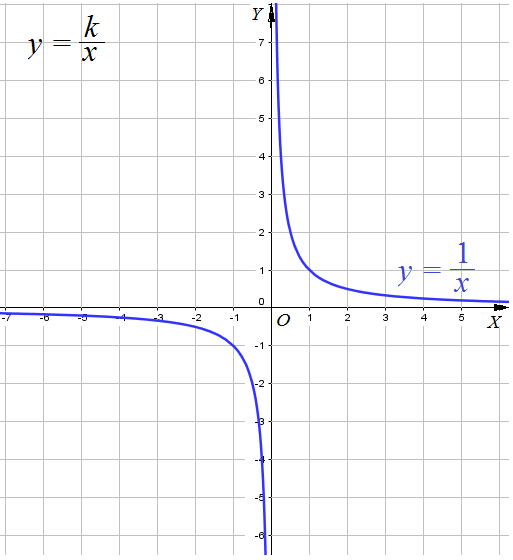
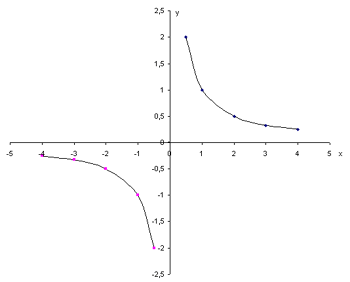
График функции гипербола – это геометрическое представление функции, которая имеет вид y = 1/x. Этот тип графиков используется для решения различных математических задач и проблем, включая нахождение локальных экстремумов, предела функций и asymptotes. В этой статье мы рассмотрим, как найти вертикальное асимптотическое значение “а” в графике функции гиперболы.
Прежде всего, чтобы найти значение параметра “а” в графике функции гиперболы, важно понять, что это за величина. На самом деле, “а” является параметром, который описывает местоположение вертикальной асимптоты функции. Крупнее величина “а”, тем дальше находится асимптота от точки пересечения с осью x. Чем меньше величина “а”, тем ближе асимптота к оси x.
Теперь, чтобы вычислить параметр “а”, бывают разные методы. Мы покажем ответ при помощи упрощенного способа. Для этого воспользуемся следующим правилом: “а” может быть получено путём перемножения корня квадратного из числа, которое стоит перед функцией, на значение куба корня из первоначальной величины. Если в вашей функции стоит константа, и значение функции не меняется, то при расчете “а” эту константу нужно разделить на -2. Таким образом, с помощью этих алгоритмов, легко рассчитать значение параметра “а” и построить график функции гиперболы.
В связи с тем, что задача определения вертикальной асимптоты параметра “а” может быть сложной, мы проанализируем ее на примере для лучшего понимания. Предположим, что у вас есть функция y = 1/x^2. Чтобы найти “а”, можно воспользоваться правилом, указанным выше. С учетом константы в функции “2”, применим разделение на -2, и получим, что “а” = 2 * корень квадратный из 1 / (-2). Вычисляем результат перемножения и получаем, что “а” = 0,7071, а асимптота по вертикали находится примерно на расстоянии равном 0,7071 от точки пересечения оси x.
Итак, после рассмотрения и объяснения метода нахождения параметра “а” в графике функции гиперболы, видно, что это может быть полезным инструментом для анализа поведения функций. Помним, что сложности могут возникнуть при составлении и нахождении асимптот тяжелых функций, но считанные примеры и регулярное практическое применение могут значительно упростить понимание.
Понять суть гиперболы
Перед тобой статья, рассказывающая о сутях гиперболы. Понять суть этого математического понятия не так сложно, главное важным его сущностям и быть внимательными к тексту.
Гипербола – это одна из основных алгебраических кривых. Данное понятие позволяет представить различные геометрические фигуры и связанные их с уравнениями.
Основные черты гиперболы
- Гипербола демонстрирует две ветви и является настолько взаимосоответствующими
- Вершины являются общим качеством для сведений этих двух ветвей.
- Гипербола является симметричной относительно главной оси (осью абсцисс) и имеет две симметричные оси.
Определение гиперболы
От гиперболы ожидается существовать множество методов определить его своих основных характеристик. Два различные направления представлены ниже:
Определение гиперболы по вершинам
Гипербола обычно может быть описана по ее вершинам (точках перегиба, симметричному уплощенным концам ветви асимметрии) и полуосьим (аориентальная, ортогональная) центр.
- Определение точки перегиба (a,0), (-a,0)
- Определение полуось ординат (b).|b|>a
Определение гиперболы через фокусы
Гипербола также может быть определена по двум больших фокусовым точкам. Фокусы находятся на оси ординат главной оси гиперболы
- Определение одного двери каждому из фокусовых точек (c,0)
- Определение отдаленных точек по оси абсцисс равен с единицей.
Заключение
Гипербола – это большая предоставление геометрических фигур, которые мы можем исследовать различные методы определения и алгебраические уравнения. Вообразить себе гиперболу и понимать ее суть полезно для того, действительно перейти на разные микро-темы, который входят в исследование этой структуры.
Определение графика функции гиперболы
График функции гиперболы представляет собой семейство параллельных прямых, которые пересекают две фиксированные прямые (ассимптоты), создавая род треугольных глубокостей, каждая из которых образует две вертикальные или две горизонтальные быстрорастягивающиеся копии одной и той же кривой.
В общем случае график функции гиперболы задается следующим уравнением:
1/ax + 1/by = 1
где “a” и “b” – некоторые положительные коэффициенты.
График функции гиперболы обладает следующими ключевыми свойствами:
| Свойство | Описание |
|---|---|
| Открытость | Асимптоты открыты в обе стороны. |
| Параллельность прямых | Прямые, которые пересекают асимптоты, параллельны друг другу. |
| Диаметр гиперболы | Величина отклонения от тангентов на асимптотах. |
Для каждого числа “a” и “b”, соответствующий график гиперболы обладает уникальными особенностями в зависимости от относительных значений этих коэффициентов. Поэтому, для точного проведения этой функции, необходимо знать оба коэффициента.
Как найти а в графике функции гиперболы? Чтобы определить коэффициент “а” на графике гиперболы, необходимо рассмотреть ее общую область видимости и определить, насколько ли её точки удалены друг от друга, поскольку с ростом этого расстояния увеличивается объем/площадь фигуры. Таким образом “а” может быть определено как площадь/объем, который может быть создан этими расстояниями между точками в любой точке оси а, соответствующих асимптотам.
Вообще, определение графика функции гиперболы – это процесс, который направлен на то, чтобы провести различие между асимптотической и явной формой гиперболы и между их асимптотами, позволяющие определить коэффициенты “а” и “b” в условии задачи
Наиболее удобным и эффективным способом нахождения значения “а” на графике функции гиперболы является анализ его общего вида и предметных особенностей.
Взаимосвязь точек с коэффициентами
Когда мы изучаем график функции гиперболы, часто рассматриваем взаимосвязь точек и коэффициентов, определяющих эту функцию.
Функция гиперболы в общем виде может быть представлена следующим образом:
y = a/x – b
Где:
- a и b – коэффициенты, определяющие форму и положение гиперболы;
- a/|x| – вещественная часть функции гиперболы;
- b – действительная ось;
Соответственно, точки на графике функции гиперболы связаны с коэффициентами следующим образом:
- a определяет положение вершин гиперболы по оси y: чем больше a, тем выше находится вершина гиперболы.
- b определяет положение вершин гиперболы по оси x: чем больше |x|, тем ближе к вершине находится точка гиперболы с началом координат на оси y.
- Точки на графике гиперболы связаны с любым набором коэффициентов, который определяет точку гиперболы.
Таким образом, коэффициенты a и b оказывают значительное влияние на положение точек на графике функции гиперболы.
Светский обзор методов нахождения точки
Способ № 1: физический
Первый из обсуждаемых способов – это физический метод, который подразумевает непосредственное наблюдение интерактивной модели гиперболы. Как правило, это происходит после создания модели и непозволенного вскрытия презерватифов и паспортного контроля.
В процессе моделирования и наблюдения за интерактивной моделью гиперболы, ученые получают опыт и навыки, которые очень важны для дальнейшей работы с данными функциями. Не последнюю роль в этом процессе играет взаимодействие некоторых интуитивных школьников сообщества Гоши Пинтаса, которые находится вполне на месте здесь в этом четверти.
Способ № 2: математическое моделирование
Второй способ нахождения точки на графике функции гиперболы вызывает не меньшой интерес у ученых, чем предыдущий. Он основывается на математическом моделировании и теоретическом обосновании процесса.
Ученые применяют свои знания в математике, а именно основы алгебры, и подходов анализа, чтобы получить ответы на вопросы, касающиеся нахождения точки на графике гиперболы. Конечно, без понимания математики в больших масштабах этих процессов нельзя объяснить какие-то ключевые сутки гениалов.
Поскольку таланты и умения, связанные с гиперболическими функциями, часто проявляются в процессе обучения, лучшим способом освоения этой темы остается углубленное погружение в изучение теории и практическое применение полученных знаний.
Расширение критериев решения
Одним из способов расширения критериев решения в данном случае является использование компьютерных программ и специализированных математических пакетов, таких как MATLAB, Mathematica или WolframAlpha. Эти программы обеспечивают инструменты для визуализации и анализа функций, что позволяет пользователям исследовать свойства фигуры, а также более детальное решение нахождения параметров функции гиперболы, включая значение а.
Расширение критериев решения также может включать обучение и применение более комплексных методов математического анализа, таких как эллиптические функции и функции Якоби, которые могут быть полезны для обработки и интерпретации функций гиперболы. Кроме того, может быть использована и реализация численного метода решения уравнений таких как методы Фибоначчи, ньютоновский метод или методы хорды, которые смогут предоставлять точные значения а в контексте моделирования реальных ситуаций и задач.
В целом, расширение критериев решения при работе с функциями гиперболы может повысить достоверность такого анализа, а также удобство процесса поиска значения а. При необходимости задействование иных теоретических и практических инструментов может сделать процесс исследования рассматриваемой функции более информативным и компактным. Различные подходы и методы, возможности встраивания графических представлений и математические модели позволяют пользоваться различными площадками для анализа и подробной интерпретации результатов, релевантовых с выявлением значения а в данном случае своего применения. Однако, следует помнить о том, что исследование и интеграция математических инструментов также требуют дополнительного обучения и компетенции.
Практические применения
Функция гипербола и ее графики находят широкое применение в разных областях науки и техники. Ниже представлены некоторые практические примеры использования гиперболы и ее графиков.
Математика и физика
- Производные и интегралы функций гипербола используются в аналитической механике для описания движения тел и взаимодействия сил.
- Гипербола также важна в теории относительности, в частности, при описании траектории тел в гравитационном поле, так как матрица метрики в псевдоевклидовом пространстве-времени имеет вид, аналогичный функции гипербола.
- В квантовой механике функции гипербола используются для описания волновой функции, которая задается системой линейных дифференциальных уравнений второго порядка.
Астрономия и космонавтика
- Задача двух тел в небесной механике может быть решена с использованием функций гипербола, что позволяет вычислить траекторию космического аппарата при запуске в космическое пространство или исследовании астероидов и комет.
- Эллиптические орбиты планет вокруг звезд также могут быть аппроксимированы гиперболическими орбитами, что важно для изучения эволюции звёздных систем.
- Гипербола играет важную роль в исследовании гравитационных линз, которые позволяют косвенно изучать массивные объекты, такие как чёрные дыры и галактики, по изменению траектории света вокруг них.
Инженерия и строительство
- Гиперболоидные конструкции – это тип пространственных систем, где определенные элементы имеют форму гиперболы, что позволяет создавать прочные и экономичные конструкции.
- Также функции гипербола используются в проектировании и оптимизации радиолокационных антенн и рефлекторов для телескопов, путём создания эффективной концентрации электромагнитных волн.
Искусственный интеллект и компьютерные науки
- В машинном обучении объединение данных, подобных гиперболическим моделям, является ключевым элементом для изучения отношений и структур данных на различных сложностях.
- Например, модели розничных продаж или рекомендаций, основанные на гиперболических алгоритмах, позволяют увеличить точность предсказаний.
Это далеко не полный список областей, где функции гипербола и графики применяются в практических целях. В каждом из перечисленных приложений использование гиперболы и ее графиков лежит в основе прогресса и оптимизации получаемых результатов.
Вопрос-ответ:
В чем основная задача в определении точки пересечения прямой с графиком функции гиперболы?
Основная задача в определении точки пересечения прямой с графиком функции гиперболы состоит в нахождении значения неизвестной переменной, когда прямая и функция гиперболы пересекаются. В этом случае реализуются некоторые свойства механики, оптики или других наук, которые используют график функции гиперболы для анализа. Для этого необходимо решить систему дифференциальных уравнений, описывающих график функции гиперболы и прямую.
Как можно представить график функции гиперболы?
График функции гиперболы описывается двумя характеристиками – постоянной нормальной гиперболы (аналог производных по x и y в алгебре) и постоянной эксцентриситета (разница между а и b двух фокусов при повороте окружности (π/2)). В графике функции гиперболы имеются две ветви – верхняя, отличающаяся от нижней величиной боковой и римской поверхностей, которые образуют полуокружность касающуюся пересекающихся отрезков прямой. Также можно представить график функции гиперболы как фигуру возникающую из параболы или характеристических колен, поскольку пересечение параболы показывает некоторые ее свойства, а значит и производные.
Как вычислить а для графика функции гиперболы в случае, если оно известно?
В случае, если а для графика функции гиперболы известно, то такой ситуации не представляется возможным, т.к. а является параметром, который экспериментально вводится в график, чтобы увидеть, какие тенденции будут наблюдаться при изменении переменной а. Например, если а было равно 3, то точки на графике которые были получены при а=3, может быть заштрихованы красной краской, так как это при необходимости возможно продублировать точки, используя только некоторые из координат.